2. Cálculo do campo elétrico

Problema 2.1

Uma pequena esfera com massa igual a 25 g e carga de 50 nC encontra-se pendurada de um fio isolador de 7 cm que está colado a um plano vertical. O plano vertical tem uma carga superficial constante $\sigma =17$ nC/cm${}^2$ e pode ser considerado infinito. Calcule o ângulo $\theta$ que o fio faz com o plano vertical.

Resolução. O campo elétrico produzido pelo plano é horizontal, com módulo constante $E=2\pi k\sigma$. A força elétrica sobre a carga pontual positiva é horizontal, para a esquerda, e com módulo (unidades SI):

$$F_{\mathrm{e}}=2\pi k\sigma q=2\times 8.988\times {10}^9\times 17\times {10}^{-5}\times 50\times {10}^{-9}\pi =0.48002\mathrm{N}$$

Sobre a esfera atuam três forças externas: a força elétrica, a tensão no fio, e o peso. O lado esquerdo da figura seguinte mostra essas forças.

Como a carga pontual fica em equilíbrio, a soma dessas 3 forças deverá ser nula. O problema podia ser resolvido definindo um sistema de dois eixos e resolvendo as duas equações das somas das componentes das forças nos dois eixos iguais a zero. No entanto, é mais fácil observar que para que a soma dos 3 vetores seja nula, se forem colocados um a seguir ao outro, como no lado direito da figura acima, deverão formar um triângulo, que neste caso é retângulo com catetos de comprimento $mg$ e $F_{\mathrm{e}}$. Como tal, a tangente do ângulo $\theta$ deverá ser igual a $F_{\mathrm{e}}/(mg)$, e o ângulo $\theta$ será:

$$\theta =\text{arctg}\left(\frac{F_{\mathrm{e}}}{mg}\right)=\text{arctg}\left(\frac{0.48002}{0.025\times 9.807}\right)={62.9}^{\circ }$$

Problema 2.2

Numa região do espaço há três cargas pontuais, $q_1=-2$ µC no ponto $(x,y,z)=(\mathrm{3,1.5,2.3})$ (em cm), $q_2=+3$ µC em $(x,y,z)=(\mathrm{3.2,1.1,1.5})$ e $q_3=-4$ µCem $(x,y,z)=(\mathrm{3.7,1.2,2.2})$. Calcule o fluxo elétrico através de uma superfície esférica de raio 3 cm, com centro no ponto (1, 0, 0).

Resolução. De acordo com a lei de Gauss, o fluxo através da superfície esférica será igual a $4\pi k$ vezes a carga total dentro da superfície esférica. Para determinar quais das três cargas estão no interior da superfície esférica, calculam-se as suas distâncias até o centro da superfície esférica:

$d_1$ $=\sqrt{{(3-1)}^2+{1.5}^2+{2.3}^2}=3.397\mathrm{cm}$

$d_2$ $=\sqrt{{(3.2-1)}^2+{1.1}^2+{1.5}^2}=2.881\mathrm{cm}$

$d_3$ $=\sqrt{{(3.7-1)}^2+{1.2}^2+{2.2}^2}=3.684\mathrm{cm}$

Como a única dessas distâncias que é menor que o raio da superfície esférica é $d_2$, a única carga no interior da superfície esférica é $q_2$ e o fluxo elétrico através da superfície esférica é

$$\mathrm{\Psi }=4\pi k{q}_2=339\times {10}^3\frac{\mathrm{N}\cdot {\mathrm{m}}^2}{\mathrm{C}}$$

Problema 2.3

Na atmosfera existe um campo eléctrico que aponta na vertical, para baixo. A nível do mar, o módulo desse campo, é aproximadamente 120 N/C e diminui em função da altura; 2 km acima do nível do mar o campo é aproximadamente 66 N/C. Que pode concluir acerca do sinal das cargas livres nos dois primeiros quilómetros da atmosfera? Calcule a densidade volúmica de carga média nessa região.

Resolução.A lei de Gauss relaciona as cargas livres numa região com o fluxo elétrico através da fronteira dessa região. Como tal, para determinar a carga livre que existe na atmosfera, devemos encontrar uma superfície fechada onde seja possível calcular o fluxo elétrico. Com os dados do problema, podemos calcular facilmente o fluxo numa superfície horizontal (perpendicular ao campo) que esteja a uma altura do nível do mar ou 2 km por cima. Usaremos uma superfície fechada com duas tampas horizontais iguais de área $A$, uma ao nível do mar e a outra 2 km por cima, com paredes laterais verticais, tal como mostra a figura seguinte:

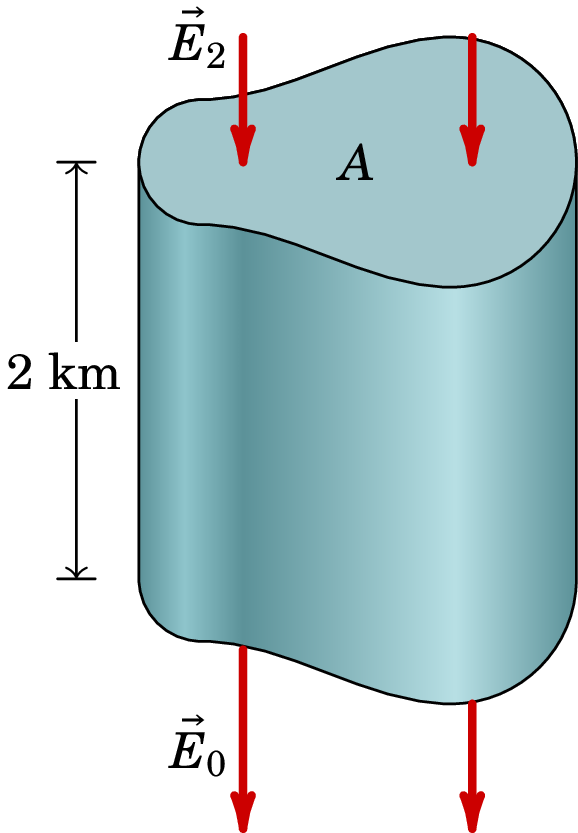
Na tampa de cima o campo elétrico, ${\overrightarrow{E}}_2$, tem módulo 66 N/C e aponta para dentro da superfície fechada. Como tal, nessa tampa há fluxo negativo igual a (unidades SI):

$${\mathrm{\Psi }}_2=-66A$$

Na tampa de baixo, o o campo elétrico, ${\overrightarrow{E}}_0$, produz fluxo positivo porque aponta para fora da superfície fechada e o valor do fluxo nessa tampa é:

$${\mathrm{\Psi }}_0=120A$$

Nas paredes laterais não há fluxo, porque as linhas de campo são tangentes a essa superfície. O fluxo total na superfície fechada é então:

$$\mathrm{\Psi }={\mathrm{\Psi }}_0+{\mathrm{\Psi }}_2=54A$$

O resultado positivo permite-nos concluir que na atmosfera (dentro da superfície fechada escolhida) existem cargas livres positivas.

Aplicando a lei de Gauss obtém-se a carga no interior da superfície fechada:

$$\mathrm{\Psi }=54A=4\pi k{q}_{\text{int}}⟹q_{\text{int}}=\frac{54A}{4\times 8.988\times {10}^9\pi }=4.7810\times {10}^{-10}A$$

Como o volume da superfície fechada, em unidades SI, é igual a $2000A$, então a densidade volúmica de carga média é:

$$\rho =\frac{4.7810\times {10}^{-10}A}{2000A}=2.391\times {10}^{-13}\mathrm{C}/{\mathrm{m}}^3$$

Comentários: Foi admitido que as linhas de campo, verticais, são paralelas entre si. Realmente as linhas verticais em dois pontos diferentes da Terra não são paralelas, porque são perpendiculares à superfície da Terra que é curva. Para obter maior precisão, a superfície fechada usada para aplicar a lei de Gauss poderia estar formada por duas esferas concêntricas: a própria superfície esférica da Terra, com raio de $R_0=6371$ km, e a segunda superfície esférica com centro no centro da Terra e raio $R_2=6373$ km, tal como mostra a figura seguinte.

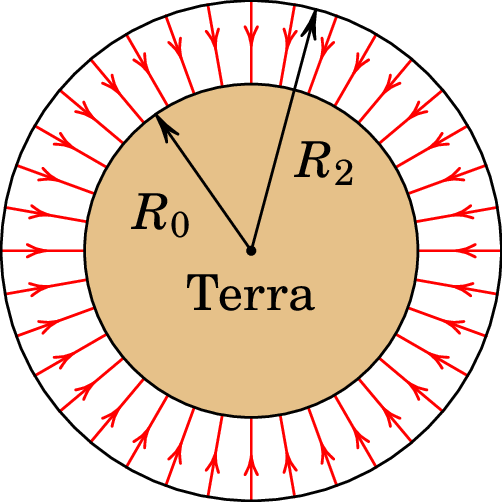
O fluxo elétrico que sai do volume entre essas duas esferas é (unidades SI):

$$\mathrm{\Psi }=120\times 4\pi R_0^2-66\times 4\pi R_2^2$$

E a densidade volúmica de carga média será:

$$\rho =\frac{\mathrm{\Psi }/(4\pi k)}{4\pi (R_2^3-R_0^3)/3}=\frac{360R_0^2-198R_2^2}{4\pi k(R_2^3-R_0^3)}=2.388\times {10}^{-13}\mathrm{C}/{\mathrm{m}}^3$$

Este resultado, mais correto, é muito semelhante ao resultado obtido admitindo linhas de campo paralelas, devido ao facto dos raios das duas esferas serem muito semelhantes.

Problema 2.4

Uma carga pontual de 5 nC encontra-se a 6 cm de um fio retilíneo muito comprido, com carga linear constante de 7 nC/cm. Calcule a força elétrica da carga sobre o fio (sugestão: calcule a força do fio sobre a carga pontual, que é mais fácil de calcular, a qual, pela lei de ação e reação, possui o mesmo módulo da força da carga sobre o fio).

Resolução. O campo elétrico de um fio retilíneo infinito, com carga linear $\lambda$ constante é na direção radial desde o fio e tem módulo

$$E=\frac{2k\lambda }{d}$$

onde $d$ é a distância desde o fio.

O módulo da força do fio sobre a carga pontual é (unidades SI):

$$F=qE=\frac{2k\lambda q}{d}=\frac{2\times 8.988\times {10}^9\times 7\times {10}^{-7}\times 5\times {10}^{-9}}{6\times {10}^{-2}}=1.05\mathrm{mN}$$

Problema 2.5

Um fio não-condutor no plano $xy$, forma uma circunferência de raio $a$ com centro na origem. O fio tem carga linear não-uniforme $\lambda ={\lambda }_0\sin \varphi$, onde $\varphi$ é o ângulo em coordenadas polares, cuja origem é o centro da circunferência. Calcule o campo elétrico na origem.

Resolução. A figura seguinte mostra um ponto P no fio e o seu vetor posição ${\overrightarrow{r}}^{\prime }$.

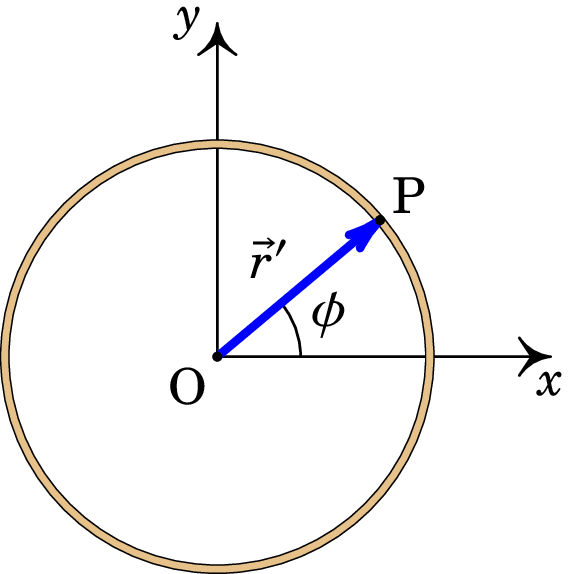
O vetor posição da origem, onde vai calcular-se o campo, é $\overrightarrow{r}=\overrightarrow{0}$ e

$$\overrightarrow{r}-{\overrightarrow{r}}^{\prime }=-{\overrightarrow{r}}^{\prime }=-a\left(\cos \varphi \hat{ı}+\sin \varphi \hat{ȷ}\right)\mathit{\hspace{1em}\hspace{1em}}\left|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right|=a$$

O comprimento infinitesimal de arco ao longo do anel é $\mathrm{d}{s}^{\prime }=a\mathrm{d}\varphi$ e o campo elétrico na origem é:

$\overrightarrow{E}$ $=k{\displaystyle {\int }_0^{2\pi }}\lambda ({\overrightarrow{r}}^{\prime }){\displaystyle \frac{\overrightarrow{r}-{\overrightarrow{r}}^{\prime }}{{|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }|}^3}}ad\varphi$

$=-{\displaystyle \frac{k{\lambda }_0}{a}}{\displaystyle {\int }_0^{2\pi }}\sin \varphi \left(\cos \varphi \hat{ı}+\sin \varphi \hat{ȷ}\right)d\varphi$

Para calcular os integrais usam-se as identidades trigonométricas:

$$\sin \varphi \cos \varphi =\frac{1}{2}\sin (2\varphi )\mathit{\hspace{1em}\hspace{1em}}{\sin }^2\varphi =\frac{1-\cos (2\varphi )}{2}$$

Que conduzem a:

$$\overrightarrow{E}=-\frac{k{\lambda }_0}{2a}{\int }_0^{2\pi }\left(\sin (2\varphi )\hat{ı}+\hat{ȷ}-\cos (2\varphi )\hat{ȷ}\right)d\varphi$$

Os integrais de $\sin (2\varphi )$ e $\cos (2\varphi )$ são iguais a zero e o resultado final é:

$$\overrightarrow{E}=-\frac{\pi k{\lambda }_0}{a}\hat{ȷ}$$

Problema 2.6

Um protão passa pela origem, em $t=0$, com velocidade $(3\hat{ı}+2\hat{ȷ})$ Mm/s, dentro de uma região onde há vácuo e campo elétrico uniforme, $\overrightarrow{E}=E\hat{ȷ}$. Determine o valor que deverá ter $E$ para que o protão atravesse o eixo dos $x$ em $x=85$ cm. (O peso do protão pode ser desprezado neste caso).

Resolução. O campo elétrico uniforme e na direção do eixo $y$ implica força externa constante e na direção $y$. Como a velocidade inicial tem componentes $x$ e $y$, o movimento será uma parábola no plano $xy$, igual à sobreposição dum movimento uniforme, na projeção no eixo $x$, e um movimento uniformemente acelerado na projeção no eixo $y$:

$$v_x=3\times {10}^6=\text{constante}\mathit{\hspace{1em}\hspace{1em}}{a}_y=\text{constante}$$

(usando unidades SI).

O tempo que o protão demora até atravessar o eixo dos $x$, em $x=85$ cm é então:

$$\mathrm{\Delta }t=\frac{\mathrm{\Delta }x}{v_x}=\frac{0.85}{3\times {10}^6}=2.833\times {10}^{-7}$$

A trajetória parabólica implica que quando o protão atravessar novamente o eixo dos $x$ terá componente $v_y$ da velocidade com o mesmo valor absoluto do seu valor inicial, mas com sinal negativo, ou seja, $v_y=-2$ Mm/s. A aceleração obtém-se a partir da seguinte equação para o movimento uniformemente acelerado:

$$a_y=\frac{v_y-v_{y0}}{\mathrm{\Delta }t}=\frac{-2\times {10}^6-2\times {10}^6}{2.833\times {10}^{-7}}=-1.412\times {10}^{13}$$

e, usando os valores da massa e da carga dum protão, a componente $y$ do campo elétrico é,

$$E_y=\frac{m{a}_y}{e}=-\frac{1.673\times {10}^{-27}\times 1.412\times {10}^{13}}{1.602\times {10}^{-19}}=-1.47\times {10}^5$$

O valor de $E$ é $-1.47\times {10}^5$ N/C.

Problema 2.7

Calcule a carga total dentro do paralelepípedo: $0\le x\le 18$ cm, $0\le y\le 20$ cm, $0\le z\le 15$ cm, onde o campo elétrico é $\overrightarrow{E}=24x\hat{ı}$ (unidades SI).

Resolução. A densidade volúmica de carga calcula-se usando a forma diferencial da lei de Gauss:

$$\rho =\frac{\overrightarrow{\nabla }\cdot \overrightarrow{E}}{4\pi k}=\frac{1}{4\pi k}\left(\frac{\partial E_x}{\partial x}+\frac{\partial Ey}{\partial y}+\frac{\partial Ez}{\partial z}\right)=\frac{6}{\pi k}$$

E, por ser constante, a carga no interior do paralelepípedo é igual à densidade volúmica de carga vezes o volume do paralelepípedo:

$$Q=\left(\frac{6}{\pi \mathrm{\hspace{0.17em}8.988}\times {10}^9}\right)\times 0.18\times 0.2\times 0.15=1.15\times {10}^{-12}\mathrm{C}=1.15\mathrm{pC}$$

Problema 2.8

Quatro cargas com valores $+q$ e $-q$ ($q>0$), encontram-se nos vértices dum quadrado de aresta $L$. Determine a expressão do campo elétrico $\overrightarrow{E}$, no ponto P (no meio da aresta do lado esquerdo), em função de $q$, $L$ e a constante $k$.

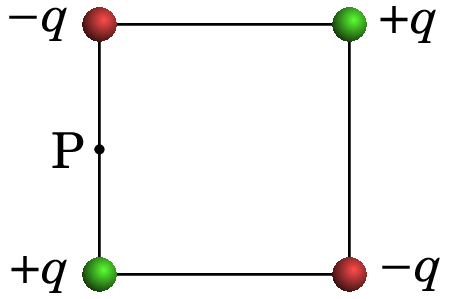
Resolução. Na figura seguinte, as quatro cargas pontuais, designadas de $q_1$, $q_2$, $q_3$ e $q_4$, produzem os quatro campos ${\overrightarrow{E}}_1$, ${\overrightarrow{E}}_2$, ${\overrightarrow{E}}_3$ e ${\overrightarrow{E}}_4$ nas direções indicadas.

Os módulos desses quatro campos determinam-se a partir da Lei de Coulomb:

$E_1=E_2={\displaystyle \frac{kq}{{(L/2)}^2}}={\displaystyle \frac{4kq}{L^2}}$

$E_3=E_4={\displaystyle \frac{kq}{d^2}}={\displaystyle \frac{kq}{L^2+{(L/2)}^2}}={\displaystyle \frac{4kq}{5L^2}}$

O campo total no ponto P é a soma vetorial dos quatro campos que, usando eixo dos $x$ na direção de $\overline{q_1{q}_4}$ e eixo dos $y$ na direção de $\overline{q_1{q}_2}$ na figura anterior, será:

$\overrightarrow{E}$ $=\left(E_1+E_2\right)\hat{ȷ}+E_3(-\cos \theta \hat{ı}-\sin \theta \hat{ȷ})+E_4(\cos \theta \hat{ı}-\sin \theta \hat{ȷ})$

$=2E_1\hat{ȷ}-2E_3\sin \theta \hat{ȷ}$

A partir da figura observa-se que

$$\sin \theta =\frac{L}{2d}=\frac{1}{\sqrt{5}}$$

substituindo esse valor e as expressões de $E_1$ e $E_3$ obtém-se:

$$\overrightarrow{E}=\frac{8kq}{L^2}\left(1-\frac{1}{5\sqrt{5}}\right)\hat{ȷ}=\frac{8kq}{25L^2}\left(25-\sqrt{5}\right)\hat{ȷ}$$