Cinemática a duas dimensões

Problemas da segunda folha complementar

(Professor Paulo Sá)

10. O vetor posição de uma partícula material é dada por

1. Determine a trajetória da partícula. Resposta A reta $y=x$.
2. Escreva as expressões analíticas de $\overrightarrow{v}$ e de $\overrightarrow{a}$ e determine os respetivos valores em função do tempo $t$. Resposta $v(t)=2\sqrt{2}(t-2)$, $a(t)=2\sqrt{2}$.
3. Classifique o movimento da partícula, indicando os intervalos de tempo em que é acelerado e em que é retardado. Resposta Movimento retilíneo uniformemente acelerado. Movimento retardado em $t<2$, repouso em $t=2$, e movimento acelerado em $t>2$.
4. Calcule a distância percorrida pela partícula durante os primeiros 5 s. Resposta 18.4 m.

11. Uma partícula material percorre uma curva plana de tal modo que as suas coordenadas cartesianas são $x=2t^3-3t^2$ e $y=t^2-2t+1$ (SI). Determine:

1. A expressão do vetor velocidade da partícula em função do tempo. Resposta $\overrightarrow{v}(t)=(6t^2-6t)\hat{ı}+(2t-2)\hat{ȷ}$ m/s.
2. O instante em que a sua velocidade se anula. Resposta 1 s.
3. A expressão do vetor aceleração da partícula em função do tempo. Resposta $\overrightarrow{a}(t)=(12t-6)\hat{ı}+2\hat{ȷ}$ m/s².
4. O instante em que a aceleração é paralela ao eixo dos $y$. Resposta 0.5 s.
5. O instante em que a aceleração da partícula se anula. Resposta Nunca.

12. Um projétil é disparado desde o solo com velocidade de valor 200 m/s segundo um ângulo de 35° com a horizontal. Determine:

1. Os vetores velocidade e posição do projétil decorridos 15 s após o lançamento. Nesse instante o projétil está a subir ou a descer? Resposta $\overrightarrow{v}(t)=163.8\hat{ı}-32.3\hat{ȷ}$ (m/s); $\overrightarrow{r}(t)=2457\hat{ı}+618\hat{ȷ}$ (m).
2. O tempo de voo do projétil. Resposta 23.4 s
3. O alcance do projétil. Resposta 3832.9 m

13. Um avião voa horizontalmente à altitude de 1000 m com velocidade de valor 400 m/s, quando deixa cair uma encomenda.

1. Quanto tempo antes de passar sobre o alvo, situado no solo, deve o avião largar a encomenda? Resposta 14.3 s.
2. Determine: (i) O valor da velocidade da encomenda ao atingir o solo. (ii) O valor da velocidade da encomenda quando se encontra a 500 m do solo. (iii) A distância na horizontal percorrida pela encomenda. Resposta (i) 423.8 m/s. (ii) 412.1 m/s. (iii) 5720 m.

14. Um projétil é disparado do solo com um ângulo de lançamento de 30° e atinge o solo a 4 km do ponto de disparo. Calcule:

1. O valor da velocidade inicial do projétil. Resposta 212.75 m/s.
2. O tempo de voo de projétil. Resposta 21.7 s.
3. A altura máxima atingida pelo projétil. Resposta 577.3 m.
4. O valor da velocidade no ponto de altura máxima. Resposta 184.25 m/s.

15. Uma bola é lançada com velocidade inicial de valor 25 m/s do topo de um edifício com 30 m de altura. Sabendo que o referido lançamento é feito segundo um ângulo de 37° acima da horizontal, determine:

1. O tempo que a bola permanece no ar. Resposta 4.45 s.
2. A distância horizontal percorrida pela bola até bater no solo. Resposta 88.9 m.
3. A altura máxima que a bola atinge em relação ao solo. Resposta 41.6 m.
4. O valor da velocidade da bola bem como a inclinação (ângulo com a horizontal) com que atinge o solo. Resposta 34.8 m/s e $-{55}^{\circ }$.

17. Um projétil é lançado do topo de um rochedo situado 200 m acima de um vale (ver figura). O vetor velocidade inicial faz um ângulo de 60° acima da horizontal e tem um módulo $v_0=60$ m/s.

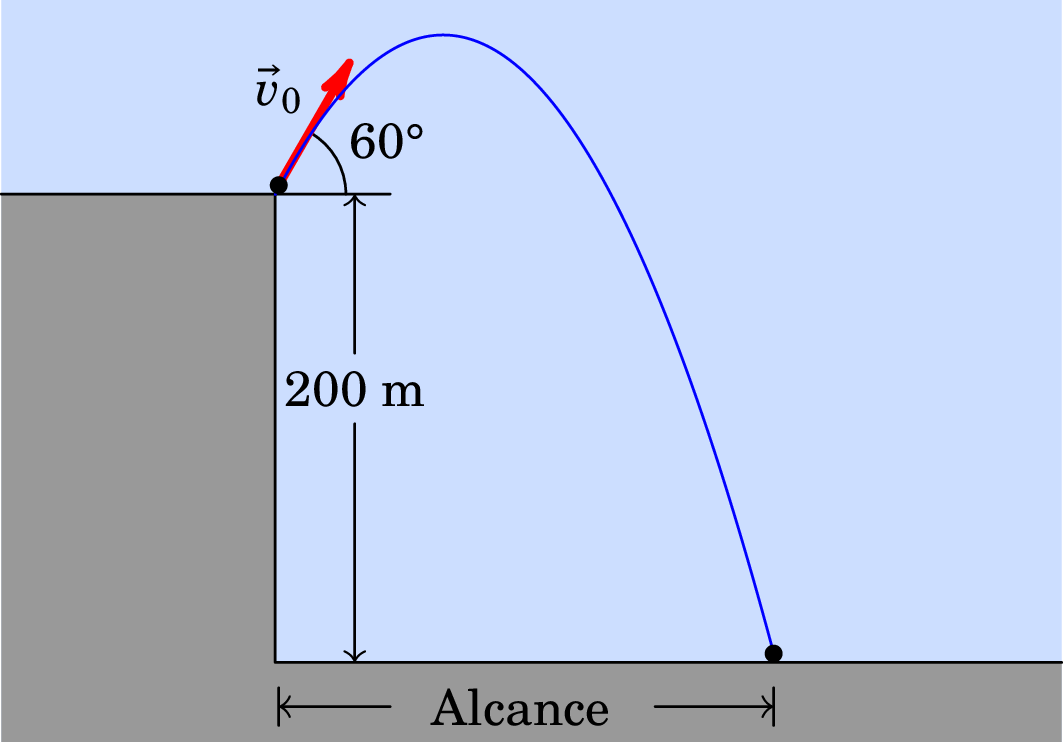
1. Qual é a altura máxima atingida pelo projétil? Resposta 337.8 m.
2. Calcule o tempo de voo. Resposta 13.6 s.
3. Qual é o seu alcance? Resposta 408.1 m.