Movimento circular e movimento relativo

Problemas do livro: Física 1, H. D. Young e R. A. Freedman

3.33. A água de um rio se escoa com velocidade de 2.0 m/s do norte para o sul. Um homem dirige um barco com motor através do rio; sua velocidade em relação à água é igual a 4.2 m/s de oeste para leste. A largura do rio é igual a 800 m.

1. Determine o módulo, a direção e o sentido da sua velocidade em relação à Terra. Resposta 4.7 m/s, 25° no sentido leste para sul
2. Quanto tempo é necessário para atravessar o rio? Resposta 190 s
3. A que distância ao sul do ponto inicial ele atingirá a margem oposta? Resposta 380 m

3.59. Uma pedra amarrada em uma corda se move no plano $xy$. Suas coordenadas são dadas em função do tempo por
  $x(t)=R\cos \omega t$, $y(t)=R\sin \omega t$
onde $R$ e $\omega$ são constantes.

1. Mostre que a distância da pedra até a origem é constante e igual a $R$, ou seja, sua trajetória é uma circunferência de raio $R$.
2. Mostre que em cada ponto o vetor velocidade é perpendicular ao vetor posição.
3. Mostre que o vetor aceleração é sempre oposto ao vetor posição e possui módulo igual a ${\omega }^{2}R$.
4. Mostre que o módulo da velocidade da pedra é constante e igual a $\omega R$.
5. Combine os resultados das partes (c) e (d) para mostrar que a aceleração da pedra possui módulo constante igual a $v^2/R$.

3.65. Um piloto de avião coloca o curso da direção de leste para o oeste com uma bússola e mantém uma velocidade em relação ao ar de 220 km/h. Depois de voar durante 0.500 h, ele se encontra sobre uma cidade a 120 km a oeste e 20 km ao sul da sus posição inicial.

1. Ache a velocidade do vento (módulo, direção e sentido). Resposta 44.7 km/h, 26.6° no sentido do sul para o oeste
2. Se a velocidade do vento fosse igual a 40 km/h do norte para o sul, em que direção o piloto deveria orientar seu curso para que pudesse se dirigir de leste para oeste. Considere a mesma velocidade em relação ao ar de 220 km/h. Resposta 10.5° no sentido do oeste para o norte

Problemas da segunda folha complementar

(Professor Paulo Sá)

18. Num parque de diversões, os passageiros viajam numa roda gigante de raio 5.0 m, com velocidade constante, completando uma volta em 4.0 s. Determine a aceleração dos passageiros. Resposta 12 m/s²

19. Num parque de diversões, uma roda gigante com raio igual a 14.0 m está a girar em torno de um eixo horizontal, passando pelo seu centro. A velocidade linear constante de uma passageira na periferia é igual a 7.0 m/s. Considere que o eixo vertical é o dos $z$. Determine o módulo, a direção e o sentido da aceleração da passageira:

1. no ponto mais baixo do movimento circular; Resposta 3.5 m/s², na direção vertical, no sentido de baixo para cima
2. no ponto mais alto do movimento circular; Resposta 3.5 m/s², na direção vertical, no sentido de cima para baixo
3. quanto tempo demora a roda gigante para completar uma volta? Resposta 12.6 s

20. Um pêndulo simples (um corpo oscilando na extremidade de um fio) descreve um arco de círculo a cada oscilação. Qual é a direção e o sentido da aceleração nas extremidades da oscilação? E no ponto médio? Explique. Resposta Nas extremidades é tangente ao círculo, no sentido para o ponto mais baixo: não há aceleração normal porque a velocidade nula, mas como a velocidade começa a aumentar, há aceleração tangencial no sentido do movimento. No ponto médio é perpendicular ao círculo, no sentido para o centro deste: a velocidade diferente de zero implica aceleração tangencial, centrípeta, mas como nesse ponto a velocidade deixa de aumentar e começa a diminuir, ou ao contrário, então a aceleração tangencial é nula.

21. Uma partícula descreve uma trajetória circular de raio unitário de acordo com a lei angular $\theta (t)=5t^2+3t$ (SI). Determine a velocidade angular, a aceleração angular e as coordenadas cartesianas da partícula no instante $t=2$ s. Resposta $\omega$ = 23 rad/s; $a$ = 10 rad/s²; $x$ = 0.647 m; $y$ = 0.763 m

22. Um avião ultraleve aponta de norte para sul e o seu indicador de velocidade em relação ao ar mostra 35 m/s. O avião está submetido a um vento de 10 m/s que sopra na direção sudoeste em relação à Terra.

1. Faça um diagrama vetorial mostrando a relação entre os vetores dados e o vetor velocidade do avião em relação à Terra. Resposta
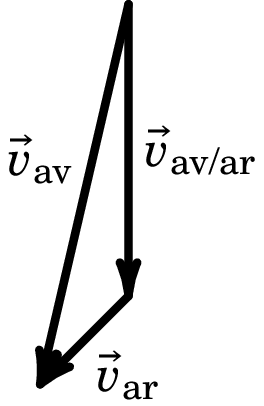
2. Usando a coordenada $x$ para leste e a coordenada $y$ para o norte, determine as componentes do vetor velocidade do avião em relação à Terra. Resposta $-7.07\hat{ı}-42.07\hat{ȷ}$ (m/s)
3. Determine o módulo, a direção e o sentido do vetor velocidade do avião em relação à Terra. Resposta $42.66$ (m/s), 9.54° do sul para o oeste

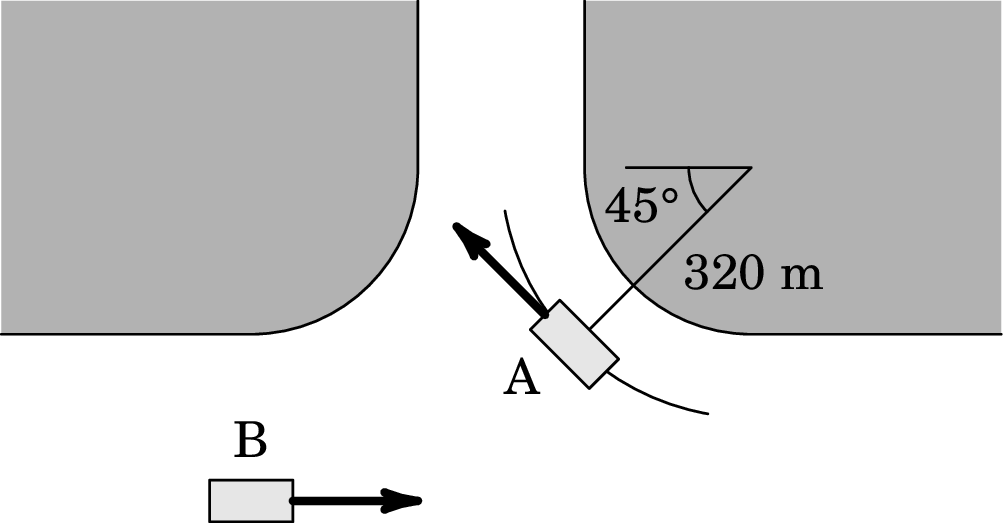
23. No instante mostrado no esquema, os automóveis A e B deslocam-se com valores das velocidades de 20 km/h e 45 km/h, respetivamente. Se B tiver uma aceleração de 0.2 m/s² enquanto A mantém um valor constante da sua velocidade, determine, para o instante da imagem:

1. os vetores velocidade e aceleração de ambos os automóveis, A e B; Resposta ${\overrightarrow{v}}_{\mathrm{A}}=-14.14\hat{ı}+14.14\hat{ȷ}$ (km/h); ${\overrightarrow{a}}_{\mathrm{A}}=0.07(\hat{ı}+\hat{ȷ})$ (m/s²); ${\overrightarrow{v}}_{\mathrm{B}}=45\hat{ı}$ (km/h); ${\overrightarrow{a}}_{\mathrm{B}}=0.2\hat{ı}$ (m/s²);
2. os valores da velocidade relativa e da aceleração relativa de A em relação a B. Resposta $v_{\mathrm{A}/\mathrm{B}}=60.8$ km/h; $a_{\mathrm{A}/\mathrm{B}}=0.15$ m/s²