Problemas da terceira folha complementar
(Professor Paulo Sá)
1. Uma partícula de massa 2 kg está sujeita a uma força definida pela expressão (SI). Sabendo que a partícula se encontrava inicialmente em repouso e na origem dos eixos, determine os vetores aceleração, velocidade e posição da partícula em função do tempo e 8 particularize para o instante s. (m/s2; (m/s); (m)
2. Uma partícula material de massa 2 g move-se ao longo de uma curva definida pelo vetor posição (cm). Calcule a força que atua na partícula no instante s. Apresente o seu resultado em unidades SI e CGS. (×10−5N) (dyn)
3. Um disco de hóquei com massa de 0.160 kg está em repouso na origem () numa superfície horizontal sem atrito. No instante , um jogador aplica sobre o disco uma força de 0.250 N paralela ao eixo ; ele continua a aplicar a força até s.
- Qual é a posição e a velocidade do disco no instante s? m; m/s.
- Se a mesma força for aplicada novamente no intervalo entre s e s, qual será a posição e a velocidade do disco no instante s? m; m/s.
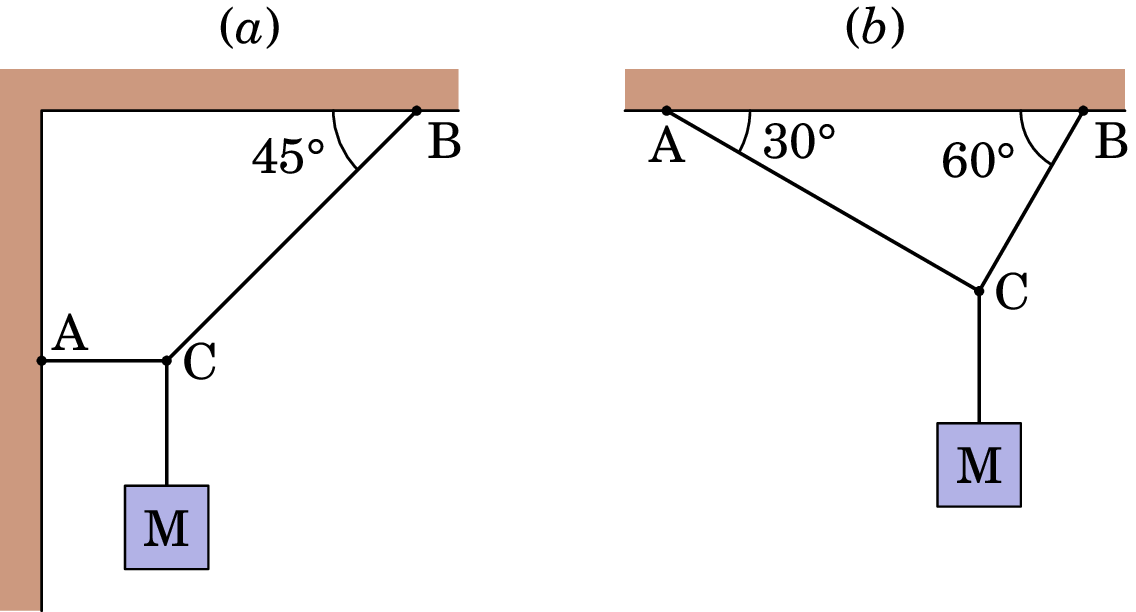
(a) 50 N e 70.7 N; (b) 25 N e 43.3 N.
7. Duas caixas, uma massa de 4.0 kg e outra de 6.0 kg, estão em repouso sobre a superfície sem atrito de um lago congelado, ligadas por uma corda leve (ver figura). Uma mulher, usando umas sapatilhas de sola áspera de modo a não escorregar, puxa horizontalmente a caixa de 6.0 kg com uma força que produz uma aceleração de 2.50 m/s2. A corda que liga as duas massas permanece tensa e horizontal durante o movimento descrito.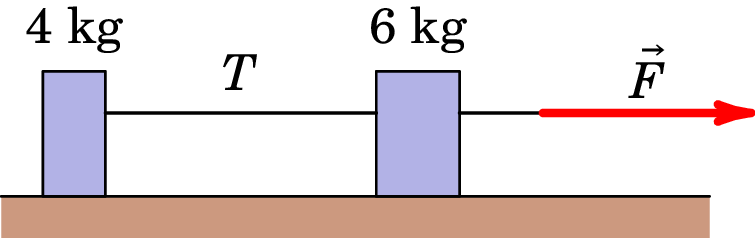
- Qual é a aceleração da caixa de 4.0 kg? 2.50 m/s2.
- Desenhe um diagrama do corpo livre para a caixa de 4.0 kg. Use esse diagrama e a segunda lei de Newton para calcular a tensão na corda que liga as duas caixas. N.
- Desenhe um diagrama do corpo livre para a caixa de 6.0 kg. Qual é a direção da força resultante sobre a caixa de 6.0 kg? Qual tem o maior módulo, a força ou a força ? Horizontal, para a direita; tem maior módulo
- Use a parte c e a segunda lei de Newton para calcular o módulo da força . 25 N.
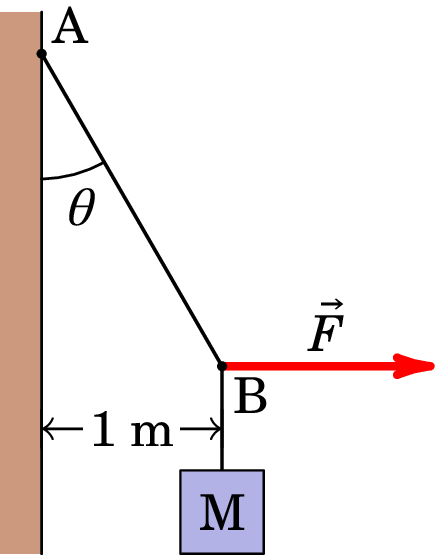
8. De acordo com o esquema representado em baixo, um corpo com massa 80 kg está preso por um fio no ponto A. No ponto B do fio aplica-se uma força horizontal , desviando-o 1 m da parede. Sabendo que AB é 2 m, determine a intensidade da força e o valor da tensão no fio, . N; N.
9. Um trabalhador está a tentar mover uma caixa de 500 N sobre um piso plano. Para iniciar o movimento, o trabalhador necessita de aplicar uma força horizontal de módulo igual a 230 N. Depois de se mover, isto é, após deixar o repouso e iniciar o movimento, a força que o trabalhador necessita de exercer para manter o movimento da caixa com velocidade constante é de apenas 200 N. Calcule o coeficiente de atrito estático e o coeficiente de atrito cinético. ; .
10. Um trabalhador está a tentar mover uma caixa puxando uma corda amarrada a esta, que faz um ângulo de 30º com a horizontal. Considere que N é o peso da caixa e o coeficiente de atrito cinético entre a superfície da caixa e a superfície sobre a qual desliza.
- Qual é a força que o trabalhador deve fazer para manter o movimento com velocidade constante? 188 N.
- O esforço que o trabalhador faz é maior ou menor do que no caso em que a força é aplicada na horizontal? Menor; a força horizontal seria 200 N.
11. Um trenó, cheio de estudantes com uma massa total igual a , escorrega para baixo numa encosta coberta de neve. A montanha possui uma inclinação relativamente à horizontal. Em todas as alíneas represente o diagrama do corpo livre.
- Considerando que o trenó está bem lubrificado de modo a não existir atrito entre este e a encosta, deduza uma expressão para a aceleração do trenó.
- Considerando agora que existe atrito entre o trenó e a encosta, e que o coeficiente de atrito é dado por , deduza uma expressão para a aceleração do trenó.
- Considerando agora que o trenó tem apenas metade dos estudantes, como irá variar a aceleração?
12. Duas caixas A e B, de massas kg e kg, respetivamente, estão ligadas entre si por uma haste de massa desprezável, conforme se representa na figura em baixo. Sabendo que o plano tem uma inclinação de 30º e que os coeficientes de atrito cinético entre as caixas A e B e a superfície do plano são, respetivamente, 0.2 e 0.3, determine a aceleração do conjunto, bem como a tensão na haste. m/s2; N.

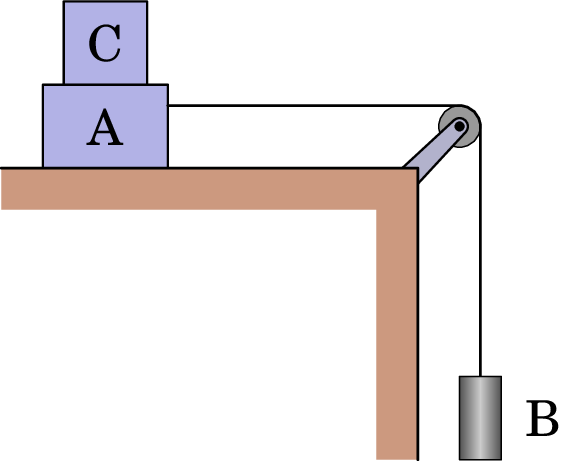 13. No esquema da figura ao lado, os corpos A e B têm massas de
10 kg e 5 kg, respetivamente, estando ligados por um fio inextensível
e de massa desprezável. O coeficiente de atrito (estático ou dinâmico,
suponha que têm o mesmo valor) entre a superfície do corpo A e a
superfície da mesa é 0.25.
13. No esquema da figura ao lado, os corpos A e B têm massas de
10 kg e 5 kg, respetivamente, estando ligados por um fio inextensível
e de massa desprezável. O coeficiente de atrito (estático ou dinâmico,
suponha que têm o mesmo valor) entre a superfície do corpo A e a
superfície da mesa é 0.25.
- Desenhe o diagrama do corpo livre de cada um dos corpos A, B e C.
- Determine o valor mínimo que a massa do corpo C tem de ter para que o conjunto dos corpos A, B e C se encontre em repouso. 10 kg
- Calcule a aceleração do sistema, bem como a tensão do fio, no caso do corpo C ser retirado. m/s2; N.
14. Uma pessoa guiando uma bicicleta faz uma curva de raio constante, com velocidade constante de 29,0 km/h. Qual o menor raio para fazê-la sem derrapar, se o coeficiente de atrito estático entre os pneus da bicicleta e o asfalto for de 0.32? 20.7 m.
15. Devido à resistência do ar, as gotas de chuva caem com uma velocidade constante a partir de certa altura. O módulo da força de resistência que o ar exerce é dada por , onde é uma constante de valor 8×10−6 N·s2/m2 e é o módulo da velocidade. Nessas circunstâncias, calcule o módulo da velocidade, em m/s, com que uma gota da chuva atinge o solo, sabendo que uma gota possui peso, em módulo, igual a 3.2×10−7 N. 0.2 m/s.
16. Uma corda é amarrada a um balde de água e o balde é posto a girar num círculo vertical de raio 0.600 m. Calcule o valor mínimo que a velocidade do balde deve ter no ponto mais elevado do círculo para que a água não seja expelida do balde. 2.4 m/s.
17. Os blocos da figura movem-se sobre uma superfície horizontal com atrito, sendo o coeficiente de atrito cinético entre o bloco com massa e a superfície sobre a qual assenta. Existe igualmente atrito entre as superfícies de ambos os blocos, sendo o coeficiente de atrito estático entre eles .
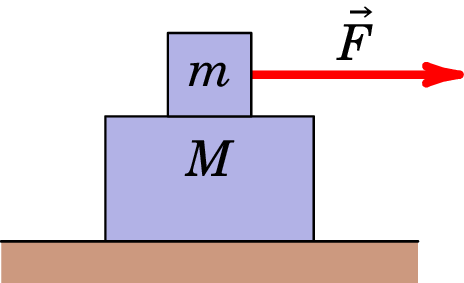
- Represente, em separado, os diagramas de corpo livre para cada um dos dois corpos e escreva a legenda das forças, indicando, se for o caso, os pares ação-reação.
- Qual é o valor máximo da força horizontal , , que se pode aplicar no bloco de cima, de modo a que os blocos permaneçam unidos, sem deslizar um relativamente ao outro?
-
Mostre que no caso de não haver atrito na superfície horizontal, essa
força máxima tem o valor: