Estática

Problemas da terceira folha complementar

(Professor Paulo Sá)

Respostas obtidas admitindo $g=9.8$ m/s².

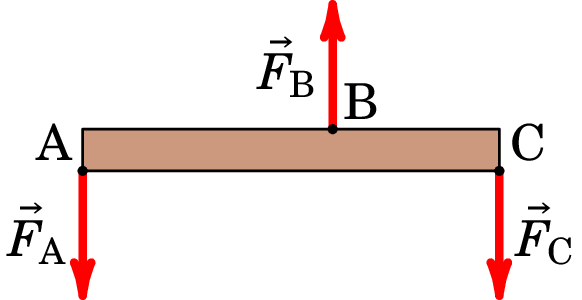
18. A barra AC, de comprimento 1 m, está sob a ação de três forças verticais, como se indica no esquema da figura abaixo. Sabendo que a distância AB é 0.6 m, os módulos das 3 forças são $F_{\mathrm{A}}=3$ N, $F_{\mathrm{B}}=5$ N, $F_{\mathrm{C}}=4$ N, e supondo desprezável o peso da barra, calcule a força que se deve exercer sobre a barra, para que esta fique em equilíbrio, bem como o seu ponto de aplicação.

19. A viga homogénea AB, representada na figura abaixo, de massa igual a 18 kg e comprimento 2 m, está suspensa horizontalmente, ligada a uma trave de sustentação (CD) por meio de dois cabos, AC e BD. Do ponto F da viga, situado a 0.5 m do ponto A, está suspenso o corpo K, com massa de 10 kg. O conjunto viga AB, corpo K e cabos de sustentação encontra-se em equilíbrio estático. Considere que os cabos AC e BD têm massas desprezáveis.

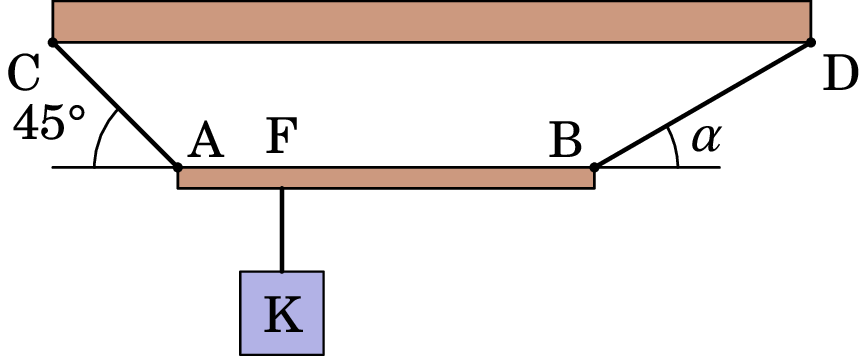
1. Determine as tensões dos cabos AC e BD. Resposta $T_{\mathrm{A}\mathrm{C}}=229$ N; $T_{\mathrm{B}\mathrm{D}}=197$ N.
2. Determine o ângulo $\alpha$. Resposta $\alpha ={35}^{\circ }$.

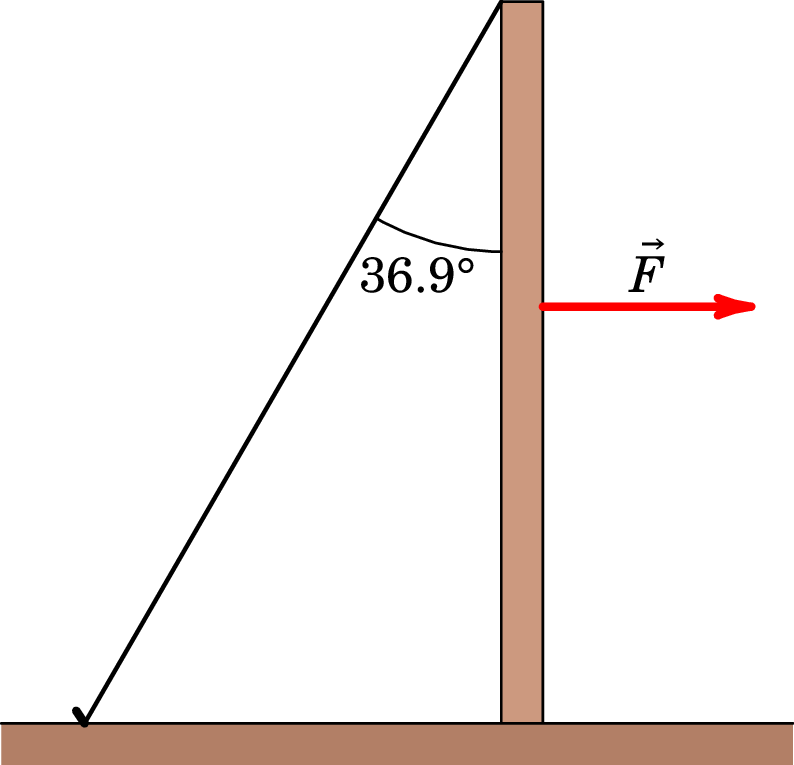
20. Um docente do MIEQ, de massa 80 kg, caminha sobre uma barra homogénea AC de massa 10 kg e comprimento 6 m. A barra está apoiada sobre dois pontos situados em A e B que distam entre si 4 m, conforme representado na figura, podendo rodar em torno do ponto B:

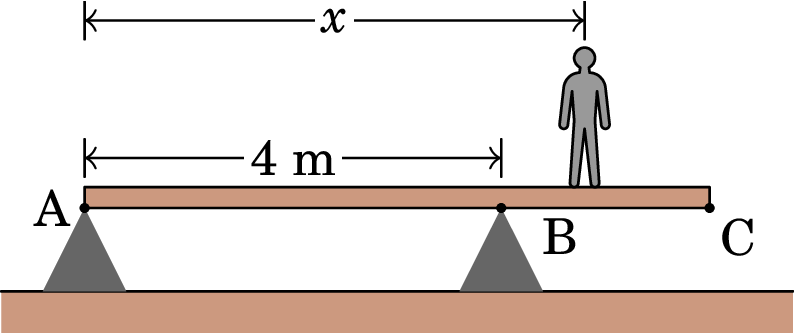
1. Calcule a distância $x$ máxima que o docente pode caminhar sobre a barra mantendo-a em equilíbrio estático. Resposta 4.125 m.
2. Determine a expressão da força de reação no ponto A (força que o ponto A exerce sobre a barra), em função da distância $x$ percorrida pelo docente. Resposta $F_{\mathrm{A}}=1078-{\displaystyle \frac{784}{3}}x$.

Problemas do livro: Física 1, H. D. Young e R. A. Freedman

11.13. Para cada um dos sistemas na figura seguinte, determine a tensão $T$ no cabo que liga a barra à parede (ou chão), e o módulo, a direção e o sentido da força exercida pelo pivô que liga a barra à parede (ou chão). Em cada caso admita que o peso da caixa é $w$. A barra é uniforme e o seu peso é também $w$.

11.82. A extremidade de um poste, de peso igual a 400 N e altura $h$, está apoiada sobre uma superfície horizontal; o coeficiente de atrito estático entre o poste e a superfície horizontal é ${\mu }_s=0.30$. A extremidade superior do poste está sustentada por uma corda amarrada à superfície horizontal e fazendo um ângulo de 36.9° com o poste (ver figura). Uma força horizontal $\overrightarrow{F}$ é aplicada sobre o poste conforme indicado.

1. Quando a força $\overrightarrow{F}$ é aplicada em seu centro, qual deve ser o módulo máximo para que o poste não comece a deslizar? Resposta 400 N.
2. Se o ponto de aplicação da força está situado a seis décimos da altura do poste a partir da sua base, qual deve ser o módulo máximo da força para que o poste não comece a deslizar? Resposta 750 N.
3. Mostre que, se o ponto de aplicação da força estiver situado num ponto muito elevado, o poste não poderá deslizar, por maior que seja o módulo da força. Determine a altura crítica para o ponto de aplicação dessa força. Resposta A altura crítica é $5h/7\approx 0.714h$.