-
A. Tutorial do Maxima
- A.1. Introdução
- A.2. Interfaces do Maxima
- A.3. Entrada e saída de dados
- A.4. Números
- A.5. Variáveis
- A.6. Listas
- A.7. Constantes
- A.8. Ficheiros de comandos
- A.9. Álgebra
- A.10. Trigonometria
- A.11. Cálculo
- A.12. Funções
- A.13. Gráficos
- Problemas
- Respostas
A. Tutorial do Maxima
A.1. Introdução
Maxima é um pacote de software livre. Pode ser descarregado livremente, funciona em vários sistemas diferentes e existe muita documentação que também pode ser copiada livremente. O sítio Web do Maxima é http://maxima.sourceforge.net
Maxima é um dos sistemas de álgebra computacional (CAS) mais antigos. Foi criado pelo grupo MAC no MIT, na década de 60 do século passado, e inicialmente chamava-se Macsyma (project MAC's SYmbolic MAnipulator). Macsyma foi desenvolvido originalmente para os computadores de grande escala DEC-PDP-10 que eram usados em várias instituições académicas.
Na década de 80, foi portado para várias novas plataformas e uma das novas versões foi denominada Maxima. Em 1982 o MIT decidiu vender Macsyma como software proprietário e, simultaneamente, o professor William Schelter da Universidade de Texas continuou a desenvolver o Maxima. Na segunda metade da década de 80 apareceram outros sistemas CAS proprietários, por exemplo, Maple e Mathematica, semelhantes a Macsyma. Em 1998, o professor Schelter obteve autorização do DOE (Department of Energy), que tinha os direitos de autor sobre a versão original do Macsyma, para distribuir livremente o código fonte do Maxima. A partir de 2001, ano em qu William Schelter morreu, um grupo de voluntários continuam a desenvolver e distribuir o Maxima.
No caso dos sistemas CAS, as vantagens do software livre são bastante importantes. Quando um método falha ou dá respostas muito complicadas é bastante útil ter acesso aos pormenores da implementação subjacente ao sistema. Por outro lado, no momento em que começarmos a depender dos resultados de um sistema CAS, é desejável que a documentação dos métodos envolvidos esteja disponível e que não existam impedimentos legais que nos proíbam de tentar descobrir ou modificar esses métodos.
A.2. Interfaces do Maxima
Existem várias interfaces diferentes para trabalhar com o Maxima. Pode ser executado desde uma "consola", ou a partir de alguma das suas várias interfaces gráficas como: wxmaxima, imaxima ou xmaxima. A figura A.1 mostra no lado esquerdo o Maxima a ser executado numa consola e no lado direito os mesmos comandos na interface gráfica imaxima. Na consola os resultados são mostrados usando apenas caracteres ASCII, mas ocupando várias linhas no caso de fracções ou potências. Nas interfaces gráficas as equações são convertidas em pequenos gráficos, tornando-as mais legíveis, mas se o resultado for muito comprido, o gráfico resultante pode tornar-se impossível de apresentar no ecrã. Os gráficos de funções normalmente são apresentados em janelas separadas, mas nas interfaces gráficas podem ser incluídos dentro da própria janela da interface.
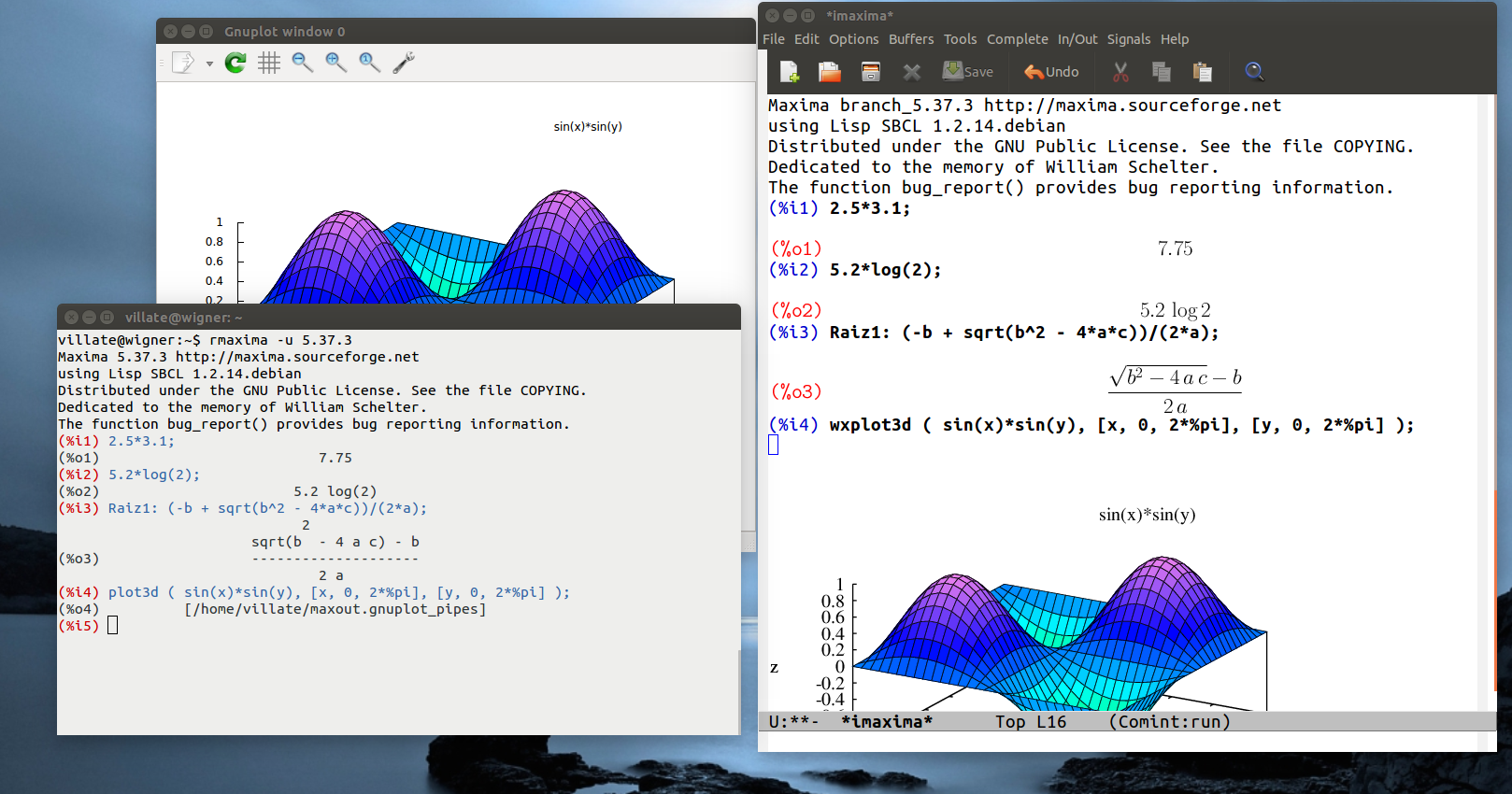
As interfaces gráficas estabelecem uma ligação (socket) com o programa Maxima, enviam através dessa ligação os comandos que o utilizador escreve, e apresentam as respostas dadas pelo Maxima.
A interface imaxima é executada dentro do editor de texto Emacs que inclui as funções próprias de um editor de texto avançado. Diferentes cores são usadas para distinguir os comandos de entrada e de saída e os comandos que já foram processados aparecem em negrito.
A.3. Entrada e saída de dados
Quando se inicia uma sessão do Maxima, aparece a marca (%i1), que quer dizer input 1. Ao lado dessa marca deve escrever-se um comando válido, terminado pelo símbolo de ponto e vírgula. Premindo a tecla de fim de linha, o comando que foi escrito fica associado a uma variável interna %i1 e o resultado é apresentado a seguir à marca (%o1), que quer dizer output 1, ficando internamente associado a outra variável %o1. A seguir aparece a marca (%i2), que permite escrever um segundo comando e assim sucessivamente. O uso mais básico do Maxima é como calculadora, para realizar contas, como nos seguintes exemplos:
(%o1)
(%i2) 5.2*log(2);
(%o2)
O resultado (%o2) mostra dois aspetos importantes no Maxima. Em primeiro lugar, o logaritmo natural de 2 não foi calculado, porque o resultado é um número irracional que não pode ser representado de forma numérica exata. A outra coisa importante é que o símbolo * e os parêntesis, que são sempre necessários nos comandos de entrada para indicar um produto e argumento de uma função, não foram escritos na saída. Isto é devido a que a saída está a ser apresentada, por omissão, num modo denominado display2d em que a saída é apresentada numa forma semelhante a como se costumam escrever expressões algébricas nos livros. Num livro, a expressão "5.2 log 2" deve ser interpretada como o produto de 5.2 vezes o logaritmo de 2; no entanto, se essa expressão fosse inserida no Maxima, dava um erro, porque a sintaxe do Maxima exige que entre o número 5.2 e a função logaritmo tem de haver algum operador e o argumento da função logaritmo (ou qualquer outra função) tem de estar entre parêntesis. A variável %o2 sim está associada internamente à expressão correta que pode ser inserida novamente no Máxima sem produzir erros de sintaxe.
Para consultar a informação do manual sobre alguma das funções ou variáveis especiais, por exemplo, a função log usada no último comando, usa-se a função describe, que pode ser abreviada com um símbolo de interrogação seguido pelo nome da função ou variável a consultar:
– Function: log (<x>)
Represents the natural (base e) logarithm of <x>.
Maxima does not have a built-in function for the base 10 logarithm or other bases. 'log10(x) := log(x) / log(10)' is a useful definition.
…
A.4. Números
Maxima aceita números reais e complexos. Os números reais podem ser inteiros, racionais, por exemplo 3/5, ou números de vírgula flutuante, por exemplo 2.56 ou 25.6e-1, que é uma forma abreviada de escrever 25.6×10−1. Números irracionais, como sqrt( 2) (raiz quadrada de 2) ou log (2 ) (logaritmo natural de 2) são mantidos nessa forma, sem serem aproximados por números de vírgula flutuante, e cálculos posteriores como sqrt(2)^2 ou exp(log(2)) produzem o resultado exato 2.
Normalmente, o tipo de número usado "contagia" os resultados subsequentes. Por exemplo, se em vez de se escrever log (2 ) fosse escrito log( 2.0), o resultado seria uma aproximação em vírgula flutuante para o logaritmo natural de 2. Outra forma de obter uma aproximação em vírgula flutuante consiste em usar a função float. Por exemplo, o resultado (%o2) obtido acima ficou associado à variável %o2. Para obter a representação em vírgula flutuante desse número, escreve-se:
(%o4)
A função float representou o produto 5.2 log(2) de forma aproximada, com 16 algarismos, usando representação de vírgula flutuante. A representação de vírgula flutuante usada no Maxima usa 64 bits para representar cada número, de forma que se conseguem obter entre 15 e 17 algarismos significativos; esse formato é conhecido como precisão dupla (em inglês, double precision).
Algo que costuma causar confusão é que esses números de vírgula flutuante estão a ser representados internamente em sistema binário e não no sistema decimal; assim sendo, alguns números que se conseguem representar de forma exata no sistema decimal como, por exemplo, 0.1, não podem ser representados de forma exata no sistema binário. É o que acontece por exemplo com a fracção 1/3 no sistema decimal, que em formato de vírgula flutuante precisava de um número infinito de algarismos para ser representada: 0.333… (num sistema de base 3 sim pode ser representada de forma exata). No sistema binário as fracções com número infinito de algarismos não são as mesmas do que no sistema decimal. Observem-se os seguintes resultados, que são perfeitamente corretos e iguais em qualquer sistema que use sistema binário com precisão dupla, mas que parecem estranhos para alguém habituado a trabalhar no sistema decimal:
(%o5)
(%i6) 6*0.1;
(%o6)
A explicação do resultado anterior é que o número 0.1 não pode ser escrito de forma exata usando 64 bits binários. Assim sendo, o resultado de multiplicar 2 vezes 0.1 não é exatamente igual a 0.2, mas o número decimal com 16 algarismos mais próximo desse resultado é 0.2000000000000000 e, por isso, o resultado aparece como se fosse 0.2, embora não seja exatamente isso. No caso de 6*0.1, em precisão dupla, o número decimal com 16 casas decimais mais próximo é 0.6000000000000001. Alguns sistemas de cálculo numérico ignoram as últimas casas decimais, apresentando o resultado como 0.6, mas sempre que estejam a usar precisão dupla binária, esse número internamente não é exatamente 0.6.
Se o número 1/3 tivesse de ser representado no sistema decimal, usando apenas 3 algarismos, a representação mais aproximada seria 333/103, ou seja, 0.333. No sistema binário com precisão dupla usam-se 52 algarismos binários e, então, o numerador tem de ser menor do que 252 e o denominador deve ser da forma . A função rationalize do Maxima mostra a representação aproximada, na forma de uma fracção, que está a ser usada para um número. Por exemplo,
(%o7)
O numerador é menor que 252 (e maior que 251) e o denominador é exatamente igual a 255. Para que o resultado fosse exatamente igual a 0.1, o denominador devia ser dez vezes maior que o numerador, ou seja, devia terminar em 70 em vez de 68, mas teve de ser usada a potência de 2 mais próxima.
Para evitar os erros numéricos inerentes ao sistema de vírgula flutuante, pode usar-se frações; por exemplo, 1/10 em vez de 0.1. Existe também um formato próprio do Maxima que permite usar um número arbitrário de algarismos significativos para números de vírgula flutuante. Esse formato chama-se big float e é indicado usando "b", em vez de "e" nos expoentes, por exemplo, o número 2.56×1020, escrito como 2.56e20, é representado em precisão dupla, com 16 algarismos significativos, e operações feitas com esse número produzem outros números de precisão dupla, com 16 algarismos significativos; mas o mesmo número, escrito como 2.56b20, é inserido no formato big-float e quando entra em operações matemáticas dá origem a outros números nesse formato, que podem ter mais algarismos significativos até um máximo fixado pelo valor da variável fpprec (floating-point precision).
A função bfloat permite converter um número para o formato big-float e o valor predefinido de fpprec é 16. Por exemplo, para obter a aproximação do resultado (%o2) com 60 algarismos significativos, usam-se os seguintes comandos:
(%o8)
(%i9) bfloat (%o2);
(%o9) 3.60436533891171573209728052144843624984298344312084369367127b0
A letra b e o número 0 no fim do resultado (%o9) indicam que o número é big-float e deve ser multiplicado por 100 = 1.
No resto deste apêndice, e em todos os capítulos do livro, todos os resultados serão arredondados automaticamente para 4 algarismos significativos. Isso consegue-se alterando o valor da variável do sistema fpprintprec
(%o10)
Internamente os números de precisão dupla continuarão a ter 16 algarismos significativos e os números big-float o número de algarismos estabelecido por fpprec; no entanto, no momento de serem apresentados no ecrã, serão arredondados para 4 algarismos significativos. Se em algum momento se pretende ver todos os algarismos associados internamente a um número, será necessário dar a fpprintprec o seu valor habitual de 0.
A.5. Variáveis
Para associar uma variável a um valor usa-se o símbolo ":" e não o símbolo de igualdade "=", que é utilizado para definir equações matemáticas. O nome das variáveis pode ser qualquer combinação de letras, números e os símbolos % e _, mas o primeiro caráter não pode ser um número. Maxima faz distinção entre maiúsculas e minúsculas. Por exemplo:
(%i12) [b, c]: [-2, -4];
(%o12)
(%i13) c;
(%o13)
(%i14) Raiz1: (-b + sqrt(b^2 - 4*a*c))/(2*a);
(%o14)
(%i15) d: sqrt(z^2 + a*c);
(%o15)
as variáveis a, b, c e Raiz1 ficaram associadas aos valores numéricos 2, −2, −4 e 2, e a variável d ficou associada a uma expressão.
Observe-se que a entrada (%i11) terminou-se com o símbolo $, em vez de ponto e vírgula. Isso faz com que o comando seja executado, mas sem que o resultado seja apresentado no ecrã. De qualquer forma a variável %o11 ficou associada ao resultado da entrada (%i11) e pode ser referido posteriormente, embora o seu valor não tenha sido mostrado. Na entrada (%i12) mostra-se como associar valores a várias variáveis com um único comando. Na entrada (%i13), quando se escreve o nome de uma variável, a saída é o valor associado a ela; se não tiver nenhum valor associado, a saída será o próprio nome da variável. Na expressão dada para a variável Raiz1, foram substituídos os valores numéricos associados às variáveis a, b e c e o resultado foi associado à variável, enquanto que a variável d ficou associada a uma expressão que depende de z, porque essa variável não estava associada a nenhum valor numérico.
Para eliminar o valor associado a uma variável usa-se remvalue; no exemplo seguinte remove-se o valor associado a a e associa-se a Raiz1 uma expressão que depende de a:
(%i17) Raiz1: (-b + sqrt(b^2 - 4*a*c))/(2*a);
(%o17)
Para eliminar os valores atribuídos a todas as variáveis escreve-se remvalue (all). Observe-se que uma variável pode estar associada a um valor numérico, a uma expressão algébrica ou a outros objetos do Maxima.
Para substituir uma variável numa expressão por um valor dado, usa-se o comando subst; por exemplo, para obter o valor da expressão Raiz1 no caso em que a é igual a 1 e aproximar o resultado exato a um número de vírgula flutuante, usam-se os seguintes comandos:
(%o18)
(%i19) float(%o18);
(%o19)
estes dois últimos comandos não modificaram a expressão associada à variável Raiz1 que continua igual.
Maxima define internamente algumas variáveis, com nomes a começar pelo símbolo %. Alguns exemplos, são as variáveis %i2 e %o2, associadas aos comandos inseridos e os seus resultados. O símbolo % representa o último resultado obtido; por exemplo, no comando (%i19) bastava escrever apenas %, em vez de %o18.
Convém não usar nomes de variáveis iguais aos nomes de funções do Maxima, embora seja possível ter funções, variáveis e outros objetos com os mesmos nomes.
Uma variável também pode estar associada a uma equação matemática; por exemplo:
(%o20)
A maior parte dos comandos inseridos são simplificados pelo Maxima antes de serem executados. Neste caso, a simplificação consistiu em reordenar as variáveis no produto m *a em ordem alfabética. Se alguma das 3 variáveis F, m ou a tivesse sido associada a algum objeto, esse objeto teria sido substituído, antes de se associar a equação resultante à variável segundalei. Neste caso nenhuma das 3 variáveis tinha sido associada a nenhum objeto; se a seguir fosse associado um valor a uma dessas variáveis, a equação que já foi associada a segundalei não é alterada, como mostram os seguintes comandos:
(%o21)
(%i22) segundalei;
(%o22)
Para substituir valores nessa equação já associada à variável segundalei, há que usar o comando subst; por exemplo,
(%o23)
Observe-se que quando se substituem várias variáveis numa expressão é necessário colocar todos os valores das variáveis, separados por vírgulas e entre parêntesis retos. O apóstrofo antes de a foi usado para impedir que a fosse substituída pelo valor associado a ela; se não tivesse sido usado o apóstrofo, a expressão "a=5" ficava "3=5" e nenhum valor seria atribuído à variável a na equação associada a segundalei:
(%o24)
A.6. Listas
Uma variável pode também ser associada a uma lista de valores, que são colocados entre parêntesis retos, separados por vírgulas. Por exemplo, o comando seguinte associa a variável quadrados a uma lista com os quadrados dos 5 primeiros números inteiros positivos:
Muitas das operações entre números realizadas no Maxima podem também ser realizadas com listas. Por exemplo, para obter outra lista em que cada elemento é a raiz quadrada do respetivo elemento na lista anterior, multiplicado por 3, basta escrever:
(%o26)
Os elementos da lista são enumerados com índices inteiros a começar por 1. Para referir-se a um elemento na lista, escreve-se o seu índice entre parêntesis retos; por exemplo, o terceiro elemento da lista quadrados é 9 que se extrai assim:
(%o27)
Uma função muito útil para criar listas é makelist, que expande uma expressão atribuindo diferentes valores a uma variável. O primeiro argumento para makelist é a expressão, o segundo argumento é o nome da variável que será substituída na expressão anterior por uma sequência de valores que vão desde um valor inicial até um valor final definidos pelo terceiro e quarto argumentos. Se houver um quinto argumento, será o incremento usado para os valores da variável; caso contrário, o incremento da variável será 1. Dois exemplos do seu uso são os seguintes
(%o28)
(%i29) cubos2: makelist ( i^3, i, 2, 6, 0.6);
(%o29)
Na primeira lista foram calculados os cubos de 1, 2, 3, 4 e 5. Na segunda, foram calculados os cubos de 2, 2.6, 3.2, 3.8, 4.4, 5.0 e 5.6. Observe-se que os cubos dos números de vírgula flutuante produziram números de vírgula flutuante, que foram automaticamente arredondados para 4 algarismos significativos, devido ao valor dado à variável fpprintprec em (%i10), enquanto que o cubo do número inteiro 2 deu como resultado também um inteiro.
O terceiro argumento para a função makelist pode ser também outra lista, com os valores que deverão ser substituídos para a variável do segundo argumento. Por exemplo, para criar uma lista com os cubos de 5, -3.2b0 e , usa-se:
(%o30)
A.7. Constantes
Existem algumas constantes importantes já predefinidas no Maxima. Os seus nomes costumam começar com o símbolo %. Três constantes importantes são o número , representado por %pi, o número de Euler, , base dos logaritmos naturais, representado por %e, e o número imaginário , representado por %i.
Tanto %pi como %e são números irracionais, que não podem ser representados de forma numérica exata, mas pode obter-se uma aproximação numérica com 16 algarismos significativos, usando a função float, ou com um número de algarismos significativos diferente, usando a função bfloat e a variável fpprec.
O número %i é útil para trabalhar com números complexos. Por exemplo, o produto entre dois números complexos:
(%o31)
Para que no resultado anterior sejam apresentadas a parte real e a parte imaginária do resultado, usa-se a função rectform (que significa rectangular form):
(%o32)
A.8. Ficheiros de comandos
As interfaces gráficas têm opções no menu que permitem guardar todos os comandos escritos durante uma sessão de trabalho no Maxima ou executar os comandos num ficheiro gravado previamente. Por exemplo, no Xmaxima essa opção é "Save Maxima Input to File" no menu "File". O ficheiro gravado com essa opção pode ser carregado mais tarde no Maxima e todos os comandos no ficheiro serão executados como se tivessem sido escritos sequencialmente (no caso do Xmaxima, com a opção "Batch File" no menu "File"). Mas é preferível usar as funções próprias do Maxima, stringout ( "ficheiro" ,input ), para gravar os comandos num ficheiro chamado "ficheiro", e batch( "ficheiro" ), para executar um ficheiro gravado previamente. Essas funções funcionam igual em qualquer interface ou na consola (consulte a documentação dessas funções).
O ficheiro criado é um ficheiro de texto simples, que pode ser editado com um editor de texto. Os comandos inseridos aparecem todos sem os identificadores (%i1), (%i2), etc, tornando necessário ter cuidado com os comandos que incluem referências a resultados anteriores, %o1, %o2, etc, já que quando o ficheiro seja executado mais tarde, os números atribuídos a esses resultados podem ser diferentes. Dentro do ficheiro podem incluir-se comentários, que começam com os símbolos /* e terminam com os símbolos */ e podem ocupar várias linhas. Os comandos introduzidos diretamente no Maxima ou escritos nesse ficheiro podem também ter espaços em branco entre números, operadores, variáveis e outros objetos, para torná-los mais legíveis e cada comando também pode ocupar várias linhas.
Uma forma eficiente de trabalhar no Maxima consiste em preparar previamente um ficheiro de texto, chamado ficheiro "batch", com os comandos que serão usados, e a seguir carrega-se esse ficheiro com a função batch ( "ficheiro" ), onde "ficheiro" é o nome completo do ficheiro. Dessa forma, se houver um erro que exige que todos os comandos sejam inseridos novamente, bastará corrigir o ficheiro e carregá-lo novamente. Nesse ficheiro escrevem-se unicamente os comandos, sem incluir as marcas (%i1), (%i2),… que serão atribuídas automaticamente quando o ficheiro seja executado.
Pode também ser útil gravar todo o que aparece no ecrã numa sessão de trabalho no Maxima. No caso de Xmaxima, usa-se a opção "Save Console to File" e se o Maxima for executado desde o editor de texto Emacs, basta gravar o ficheiro. Esse ficheiro serve como informação, mas não pode ser utilizado como ficheiro batch.
Alguns comandos que costumam ser usados novamente em sessões de trabalho posteriores, por exemplo, a definição de uma função usada com frequência, podem ser colocados num ficheiro que depois é carregado usando-se a função batch. Se o nome do ficheiro não inclui o caminho para o diretório onde se encontra, será procurado primeiro no diretório atual e logo num diretório onde o Maxima procura ficheiros executáveis do utilizador. A localização desse diretório pode ser descoberta examinando o conteúdo da variável maxima_userdir.
Para que um ficheiro batch seja carregado automaticamente cada vez que se inicia uma nova sessão do Maxima, deverá ter o nome maxima-init.mac e estar localizado no diretório onde são procurados ficheiros executáveis do utilizador. Por exemplo, as sessões de Maxima nos capítulos deste livro são executadas num sistema onde existe um ficheiro maxima-init.mac, no diretório "/home/username/.maxima", com o seguinte conteúdo:
fpprintprec: 4$
cada vez que se inicia o Maxima, a variável especial ratprint fica com valor lógico falso, que faz com que não apareçam advertências de que um número de vírgula flutuante foi aproximado automaticamente para um número racional, e a variável especial fpprintprec fica com valor de 4, o que faz com que os resultados de vírgula flutuante sejam arredondados para 4 algarismos significativos. Qualquer outro comando válido do Maxima pode ser incluído nesse ficheiro, mas há que ter cuidado de não incluir comandos que produzam erros que podem bloquear o arranque do Maxima.
A.9. Álgebra
As expressões podem incluir operações matemáticas com variáveis abstratas. Por exemplo:
Essas expressões podem ser depois manipuladas, produzindo novas expressões. Por exemplo:
(%o34)
O símbolo de igualdade usa-se para definir equações matemáticas; por exemplo:
(%o35)
Para encontrar as raízes de um polinómio pode usar-se a função allroots; por exemplo:
(%o36) ,
Há duas raízes complexas e uma real. As três raízes foram colocadas numa lista. Para extrair, por exemplo, o lado direito na terceira raiz na lista, usa-se a função rhs (right-hand side):
(%o37)
A variável x permanece indefinida, já que o sinal de igualdade não é usado para associar valores numéricos às variáveis. As raízes obtidas em (%o36) são aproximadas e não exatas. Em alguns casos, as raízes podem ser calculadas de forma algébrica exata, usando o comando solve que também resolve outros tipos de equações diferentes de polinómios. Por exemplo, o uso de solve para encontrar as raízes do polinómio acima é o seguinte:
(%i39) float ( rectform (%));
(%o39) ,
O resultado exato encontrado pela função solve ocupa várias linhas e não foi apresentado no ecrã; apenas foi apresentada a aproximação dessas raízes para números de vírgula flutuante.
Lembre-se que quando já está associado um valor a uma variável, deverá escrever-se um apostrofo antes do nome dessa variável para poder ser usada como variável algébrica indefinida. Ou também pode eliminar-se o valor associado à variável usando a função remvalue.
Para resolver um sistema de equações, que podem ser lineares ou não lineares, o primeiro argumento para o comando solve deve ser uma lista com as equações e o segundo uma lista com os nomes das variáveis; a lista das equações ou cada equação podem ser previamente associadas a alguma variável. Por exemplo:
(%i41) eqB: (2 + 8 + 5 + 1)*x2 - 8*x1 = -4$
(%i42) solve ( [eqA, eqB], [x1, x2] );
(%o42)
O resultado foi uma lista dentro de outra lista, porque a primeira lista engloba os valores das variáveis e a segunda lista as várias soluções do sistema, que neste caso foi apenas uma. O sistema anterior também podia ter sido resolvido com o comando linsolve, em vez de solve, por tratar-se de um sistema de equações lineares.
Maxima inclui outras funções para trabalhar com expressões algébricas. Por exemplo, para expandir produtos e potências de expressões usa-se expand.
(%o43)
A função factor é usada para fatorizar expressões. Outras funções úteis para simplificar expressões algébricas são ratsimp, radcan e xthru. Entre várias expressões equivalentes o conceito de simplicidade é relativo e depende do gosto de cada um; assim sendo, diferentes funções de simplificação podem produzir expressões diferentes, embora equivalentes. Em cada caso é conveniente experimentar com diferentes funções para decidir a forma preferida para apresentar uma expressão. Também algumas funções, como por exemplo ratsimp, podem produzir resultados mais simples quando aplicadas uma segunda vez.
A função subst, que já foi usada para substituir valores numéricos numa expressão, pode ser usada também para substituir outras expressões; por exemplo, para substituir por , e pelo valor numérico 2 no resultado (%o43), escreve-se:
(%o44)
para reduzir tudo a um denominador comum e guardar o resultado na variável res uma possibilidade é escrever:
(%o45)
As expressões algébricas são representadas internamente como listas; como tal, é possível usar nelas as funções do Maxima para listas. Por exemplo, a função length calcula o comprimento de uma lista; essa função aplicada a uma expressão calcula o número de termos; por exemplo
(%o46)
Como a expressão res foi reduzida a uma única fração, os dois termos contabilizados por length são o denominador e o numerador; assim sendo, a função first, que extrai o primeiro elemento de uma lista, mostrará unicamente o numerador da expressão associada a res
(%o47)
e o comprimento dessa nova expressão é:
(%o48)
Cada um dos sete elementos dessa lista são os sete termos somados em (%o47). Uma expressão que já não pode ser separada em mais partes, por exemplo, , chama-se um átomo; as funções que esperam uma lista como argumento produzem uma mensagem de erro quando lhes for dada como argumento um átomo. A função atom diz se o seu argumento é um átomo ou não.
Outra função muito útil para trabalhar com listas é a função map, que permite aplicar uma função dada a cada elemento de uma lista. No caso de uma expressão racional, pode usar-se para aplicar uma função ao numerador e ao denominador. Por exemplo, observe-se a diferença entre expandir uma expressão racional e expandir o numerador e denominador por separado:
(%o49)
(%i50) expand(frac1);
(%o50)
(%i51) map ( expand, frac1 );
(%i51) map ( expand, frac1 );
(%o51)
A.10. Trigonometria
A tabela A.1 mostra os nomes das principais funções trigonométricas no Maxima. As funções que esperam que o argumento de entrada seja um ângulo, interpretam o argumento de entrada em radianos e não em graus, já que Maxima conhece algumas propriedades dessas funções, tal como as suas séries de potências, que são válidas apenas quando o ângulo é medido em radianos. O resultado das funções inversas é um ângulo em radianos.
| Função | Descrição |
|---|---|
| sin(x) | Seno |
| cos(x) | Cosseno |
| tan(x) | Tangente |
| sec(x) | Secante |
| csc(x) | Cossecante |
| cot(x) | Cotangente |
| asin(x) | Seno inverso |
| acos(x) | Cosseno inverso |
| atan(x) | Tangente inversa |
| atan2(y,x) | Tangente inversa |
| asec(x) | Secante inversa |
| acsc(x) | Cossecante inversa |
| acot(x) | Cotangente inversa |
Todas as funções inversas com um único argumento, produzem um ângulo entre 0 e . Por exemplo:
(%o52)
(%i53) acos(-1/2);
(%o53)
Observe-se que o resultado foi exato quando o argumento da função foi escrito de forma exata, usando um número racional. A função atan2 necessita dois argumentos, as coordenadas cartesianas e de um ponto, e produz um ângulo que pode estar em qualquer um dos 4 quadrantes (entre e ), que é o ângulo entre o segmento que passa pela origem e esse ponto e o semieixo positivo dos . Para converter o ângulo em radianos para graus, multiplica-se por 180 e divide-se por , como no exemplo seguinte:
(%o54)
Para passar de graus para radianos, multiplica-se por e divide-se por 180. Por exemplo, o seno de 60° é:
(%o55)
Existem também algumas funções para simplificar expressões trigonométricas. A função trigexpand serve para expandir senos ou cossenos de somas ou diferenças de ângulos:
(%o56)
A função trigreduce tenta expandir a expressão de forma a que cada termo só tenha uma função trigonométrica.
(%o57)
A função trigsimp aplica a identidade trigonométrica e as relações entre as funções trigonométricas, para tentar escrever uma expressão apenas em termos das funções seno e cosseno. Por exemplo:
(%o58)
(%i59) trigsimp(%);
(%o59)
A.11. Cálculo
A forma mais simples de representar funções matemáticas no Maxima consiste em usar expressões. Por exemplo, para representar a função , associa-se a expressão no lado direito a uma variável
(%o60)
A derivada da função , em ordem a , calcula-se usando a função diff
(%o61)
e a primitiva em ordem a calcula-se com a função integrate
(%o62)
O valor da função num ponto, por exemplo, , pode ser calculado substituindo por 1 com a função subst, ou com a função at
(%o63)
Maxima também permite definir funções, que serão discutidas com mais pormenor na seguinte secção, e que podem ser usadas para representar funções matemáticas. Por exemplo, a mesma função também podia ter sido definida assim:
(%o64)
O valor da função num ponto neste caso obtém-se mais diretamente, mas no cálculo da derivada e a primitiva é necessário escrever a função e a variável no seu argumento:
(%o65)
(%i66) diff (f(x), x);
(%o66)
(%i67) integrate (f(x), x);
(%o67)
Observe-se que nos comandos (%i66) e (%i67) está realmente a derivar-se ou integrar-se uma expressão para e não uma função do Maxima. O que acontece é que quando se escreve f (x ) e x não está associada a nenhum valor, a função produz como resultado uma expressão que é logo derivada ou primitivada pelas funções diff ou integrate. Mas algumas funções do Maxima não produzem como resultado expressões matemáticas; por exemplo:
(%o68)
Os valores em diferentes pontos, por exemplo , são obtidos sem problema, mas as funções diff e integrate não conseguem calcular a derivada e a primitiva, porque o resultado de h(x) não é uma expressão matemática (inclui comandos específicos do Maxima: if, then e else):
(%o69)
Quando a função diff não consegue obter a derivada da expressão dada, tal como aconteceu no caso anterior, dá como resultado o mesmo comando de entrada, que neste caso foi simplesmente apresentado de forma diferente no ecrã, mas internamente o conteúdo da variável %o69 é diff(if x < 0 then x/2 else x^2,x).
Quando uma expressão depende de várias variáveis, diff calcula a derivada parcial:
(%o70)
Um integral definido calcula-se também com a função integrate, mas incluindo os limites de integração a seguir à variável de integração; por exemplo:
(%o71)
A.12. Funções
Uma função no Maxima é um programa com algumas variáveis de entrada e uma saída. O Maxima tem uma linguagem simples de programação que permite definir essas funções e também é possível usar a linguagem Lisp, que é a linguagem em que o código do Maxima está escrito. É ainda possível redefinir qualquer uma das funções que já têm sido referidas; por exemplo, se na versão do Maxima a ser usada alguma função tem um bug que já foi corrigido numa versão mais recente, é possível carregar a nova versão dessa função e, a menos que introduza conflitos com outras funções antigas, deverá funcionar corretamente.
Um primeiro exemplo consiste na criação de uma função fact que calcule o fatorial de um número inteiro (no Maxima basta colocar o símbolo ! após um número para obter o seu fatorial, mas aqui será criada outra versão do mesmo programa):
(%o72)
(%i73) fact(6);
(%o73)
Não é preciso usar nenhum comando para produzir a saída, já que a saída de um programa é sempre a que for produzida pelo último comando executado pela função. Uma função pode usar-se a si própria de forma recursiva, como foi feito neste exemplo.
Vários comandos do Maxima podem ser agrupados, entre parêntesis e separados por vírgulas. Esses comandos são executados sequencialmente e o resultado do último comando será o resultado de todo o grupo; os comandos podem ser indentados e podem ocupar mais do que uma linha. O seguinte exemplo define uma função que soma todos os argumentos que lhe sejam dados:
for i:1 thru length(v) do
(s : s + v[i]),
s)$
(%i75) soma (45,2^3);
(%o75)
(%i76) soma (3,log(x),5+x);
(%o76)
Usou-se uma lista no argumento da função, indicando que a função admite qualquer número de variáveis de entrada (ou até nenhuma) e todas as variáveis de entrada são colocadas numa lista associada á variável local v. A função block foi usada para definir outra variável local s, com valor inicial 0, que no fim terá a soma de todas as variáveis de entrada. O primeiro elemento dado a block deve ser uma lista, que pode ter qualquer número de variáveis locais, com ou sem valores iniciais, e a seguir a essa lista vem o resto da função. O comando for itera a variável local i, neste caso desde 1 até o comprimento da lista v e com incrementos, por omissão, de 1 (a opção step pode usar-se para modificar o incremento por omissão). Quando as iterações terminam, escreve-se o nome da variável s para que o valor associado a ela fique como saída do programa.
Quando se usa uma função que não existe, não é produzida nenhuma mensagem de erro, mas na saída do comando aparece a mesma função sem alteração; por exemplo:
(%o77)
Outras funções do Maxima também retornam o mesmo comando de entrada quando não é possível obter um resultado. Por exemplo:
(%o78)
Esse comportamento das é muito útil, porque assim é possível alterar mais tarde os valores dos argumentos e avaliar novamente a função. Por exemplo, neste último resultado, substituindo a variável x pelo número de vírgula flutuante 2.0, o logaritmo já será calculado:
(%o79)
A.13. Gráficos
A.13.1. Funções de uma variável
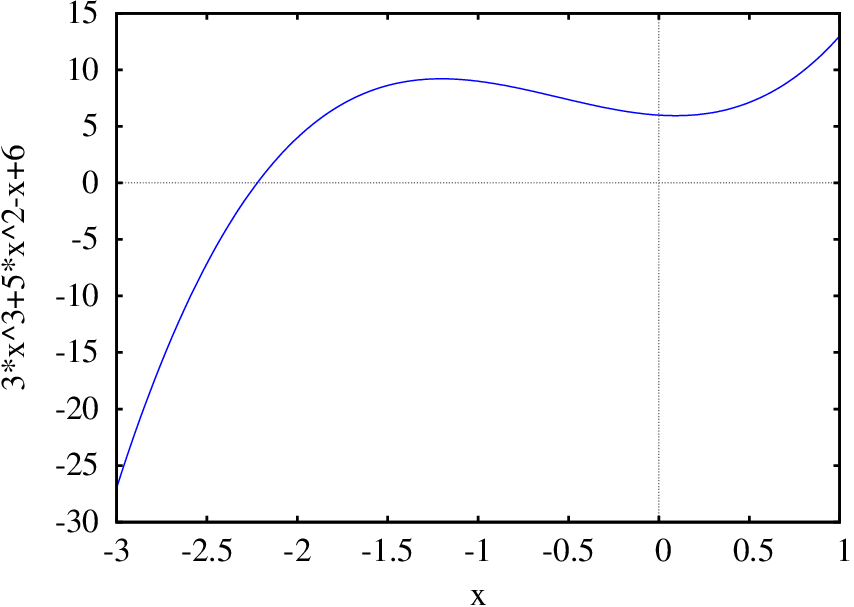
Para traçar o gráfico de uma ou várias funções de uma variável, usa-se o comando plot2d. Por exemplo, para desenhar o gráfico do polinómio , no intervalo de entre −3 e 1, usa-se o comando:
o resultado (%o80) (que não foi mostrado aqui) é o nome de um ficheiro auxiliar que foi criado e logo submetido a um programa externo (Gnuplot) que interpreta os comandos nesse ficheiro e mostra o gráfico numa janela separada (figura A.2). Passando o rato sobre um ponto no gráfico, mostram-se as coordenadas desse ponto.
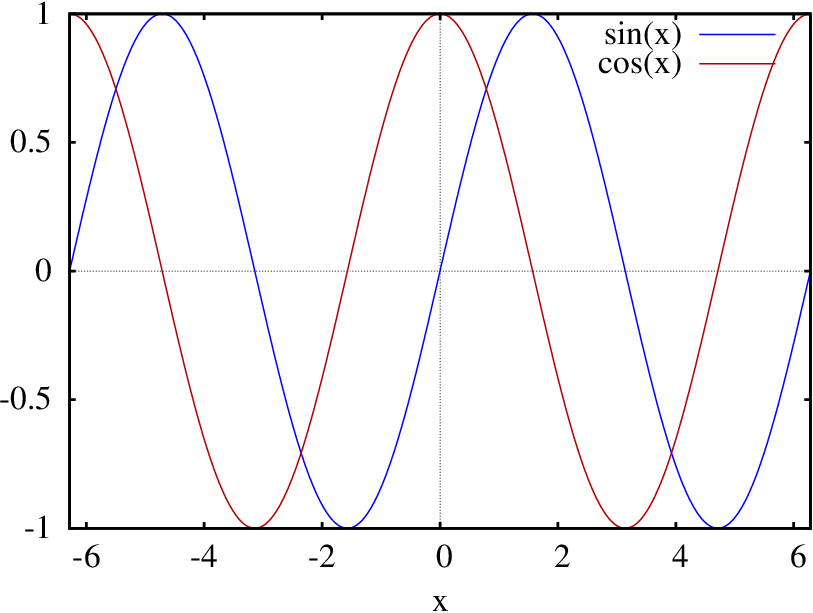
Para traçar os gráficos de várias funções num mesmo gráfico, colocam-se as funções dentro de uma lista. Por exemplo:
O resultado é apresentado na figura A.3.
A.13.2. Criação de ficheiros gráficos
A partir da versão 5.32, existem três opções, pdf_file, png_file e ps_file que permitem gravar o gráfico num ficheiro em formato PDF, PNG ou PostScript.
Por exemplo, para gravar o gráfico produzido pelo comando (%i80) num ficheiro PNG, usa-se o comando:
(%o82) [/home/username/maxout.gnuplot, /home/username/funcao1.png]
O resultado mostra que foram criados dois ficheiros; o primeiro com nome maxout.gnuplot contém comandos do Gnuplot que produzem o gráfico e gravam o resultado no segundo ficheiro, com nome funcao1.png. Como não foi indicado um caminho completo para o nome do ficheiro na opção png_file, o ficheiro foi criado no diretório do utilizador. O ficheiro maxout.gnuplot é um ficheiro de texto simples, que pode ser editado com um editor de texto e executado, independentemente do Maxima, com o programa gnuplot:
Para produzir a figura A.2 em formato PDF, usa-se o seguinte comando:
A.13.3. Gráficos de pontos
É possível também criar um gráfico de um conjunto de pontos num sistema com duas coordenadas. As duas coordenadas de cada ponto podem ser indicadas como uma lista dentro de outra lista com todos os pontos; por exemplo, para criar um gráfico com os três pontos (1.1, 5), (1.9, 7) e (3.2,9), as coordenadas dos pontos podem ser associadas a uma lista p:
Para criar o gráfico, é necessário dar à função plot2d uma lista que comece com a palavra-chave discrete, seguida pela lista de pontos. Neste caso não é obrigatório indicar o domínio para a variável do eixo horizontal:
O gráfico é apresentado na figura A.4.
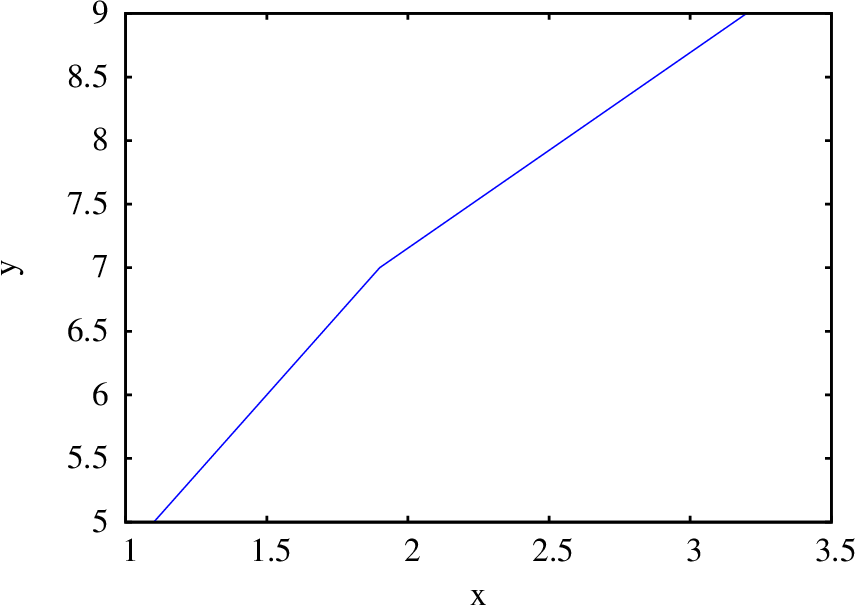
Por omissão, os pontos são ligados entre si por segmentos de reta; para mostrar apenas os pontos, sem segmentos de reta, usa-se a opção style, com o valor points.
A.13.4. Pontos e funções
Podem também combinar-se o gráfico de um ou vários conjuntos de pontos com o gráfico de uma ou várias funções. Nesse caso, cada conjunto de pontos será representado por uma lista a começar com a palavra-chave discrete, como na secção anterior, e cada função será representada por uma expressão; as listas de pontos e expressões deverão ser colocadas dentro de outra lista e será necessário indicar o domínio para a variável independente (eixo das abcissas); é possível também especificar o contradomínio para a variável dependente (eixo das ordenadas), através da opção y.
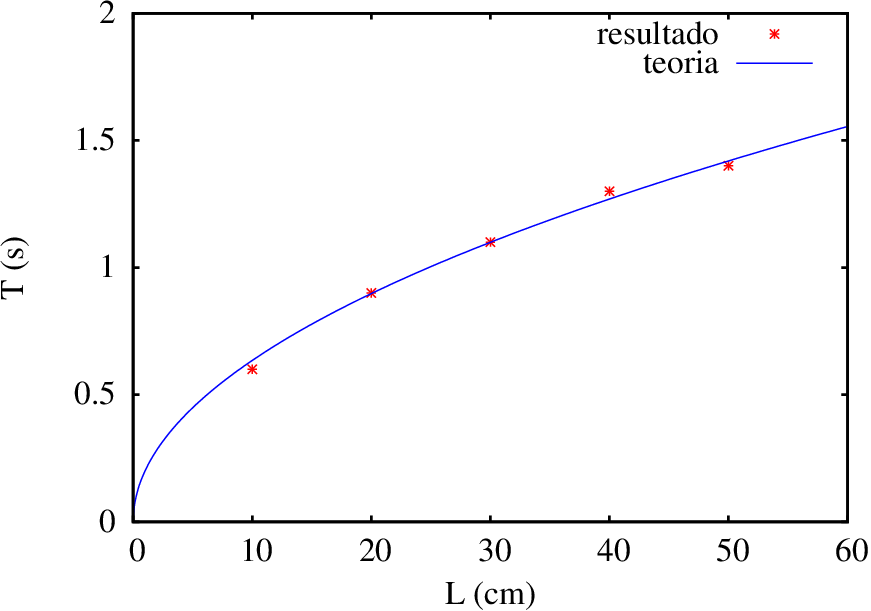
Exemplo A.1
Represente num gráfico os resultados experimentais na tabela, junto com a curva teórica esperada: , com cm/s2
| (cm) | (s) |
| 10 | 0.6 |
| 20 | 0.9 |
| 30 | 1.1 |
| 40 | 1.3 |
| 50 | 1.4 |
Resolução. O gráfico dos resultados, junto com a curva esperada, pode ser obtido com os seguintes comandos:
(%i87) plot2d([[discrete, tabela], 2*%pi*sqrt(L/980)], [L,0,60], [style, points, lines], [color, red, blue], [point_type, asterisk], [legend, "resultado", "teoria"], [xlabel, "L (cm)"], [ylabel, "T (s)"], [y,0,2]);
A opção style em (%i87) indica que o primeiro conjunto de pontos será ser representado por pontos e a expressão a seguir será representada com segmentos de recta. O gráfico é apresentado na figura A.5. A opção y é especialmente útil para limitar os valores apresentados no eixo vertical, no caso de funções com assimptotas verticais.
A.13.5. Funções de duas variáveis
Para traçar gráficos de funções de duas variáveis, em 3 dimensões, usa-se o comando plot3d. Por exemplo, o gráfico na figura A.6 foi produzido com o comando:
Deslocando o rato enquanto o botão do lado esquerdo estiver premido, a superfície roda podendo ser vista desde diferentes direções. O comando plot3d também aceita uma lista de várias funções a serem representadas no mesmo gráfico. Também pode usar-se uma lista de 3 funções, que representam as 3 componentes do vector posição que define uma superfície em 3 dimensões (gráfico paramétrico).
Existem muitas outras opções para as funções plot2d e plot3d e outras funções gráficas. A secção "Plotting" no Manual do Maxima descreve essas funções: http://maxima.sourceforge.net/docs/manual
O gráfico mais elaborado neste livro é a figura 7.13, que foi produzida com os seguintes comandos:
(%i90) V: -integrate (Ft,s,0,s)/0.3$
(%i91) se: map (lambda([x],rhs(x)), float (realroots (Ft)))$
(%i92) He: makelist (subst (s = v, V), v, se)$
(%i93) p: makelist(map(lambda([x],rhs(x)),float(realroots(V=H))), H, [He[1],250,He[3], 70])$
(%i94) l1: [discrete, [[-4,He[1]], [p[1][1],He[1]]]]$
(%i95) l2: [discrete, [[-4,250], [p[2][1],250]]]$
(%i96) l3: [discrete, [[p[2][2],250], [p[2][3],250]]]$
(%i97) l4: [discrete, [[p[3][2],He[3]], [p[3][5],He[3]]]]$
(%i98) l5: [discrete, [[p[4][2],70], [p[4][3],70]]]$
(%i99) l6: [discrete, [[p[4][4],70], [p[4][5],70]]]$
(%i100) rep: [discrete,[l1[2][2],l2[2][2],l3[2][1],l3[2][2],l4[2][1],l4[2][2],l5[2][1],l5[2][2],l6[2][1],l6[2][2]]]$
(%i101) max: [discrete,[[se[1],He[1]],[se[3],He[3]]]]$
(%i102) min: [discrete,[[se[2],He[2]],[se[4],He[4]]]]$
(%i103) plot2d ([V,l1,l2,l3,l4,l5,l6,rep,max,min], [s,-4,7.5], [ylabel,"V(s)"], [legend,false], [color,blue,red,red,red,red,red,red,red,black,black], [style,lines,lines,lines,lines,lines,lines,lines,points,points,points], [point_type,bullet,asterisk,circle],[label,["-32.9",0.3,-65], ["51.1",5.5,20], ["70",0.8,85], ["70",5.6,85], ["114.7",0.6,132], ["114.7",5.4,132], ["250",-3.99,270], ["250",3.5,270], ["356.4",-3.9,375], ["356.4",3.4,375]])$
A função a ser representada é menos a primitiva da força , dividida pela massa, 0.3. Na lista se foram extraídos os valores de em que a força é nula, ou seja, os pontos onde tem máximos e mínimos locais. A lista p são as coordenadas desses máximos e mínimos e dos pontos onde é igual a 70 e a 250. Com as coordenadas desses pontos foram construídas 6 linhas horizontais, l1… l6 e 3 conjuntos de pontos, rep, max e min, com as coordenadas dos pontos onde é igual a 70 e a 250, os máximos locais e os mínimos locais. A seguir foi criado o gráfico mostrando a função, as linhas horizontais e os três conjuntos de pontos usando objetos diferentes e finalmente foi usada a opção label para escrever alguns números em algumas partes do gráfico.
Problemas
- Trace o gráfico de cada uma das seguintes funções,
usando intervalos que mostrem bem a forma das funções.
- O gráfico da função apresenta dois pontos extremos (um mínimo local e um máximo local). Desenhe o gráfico dessa função. Sabendo que a derivada da função é nula nos dois pontos extremos, calcule as coordenadas e desses dois pontos.
- Encontre a equação da circunferência que passa pelos pontos (−2, 7), (−4, 1) e (4, −5). Sugestão: a forma geral da equação será . Para encontrar as três constantes , e , substitua as coordenadas de cada um dos 3 pontos dados, e resolva o sistema das 3 equações obtidas.
- Defina uma função fib(n) em Maxima para
calcular qualquer número na sequência de Fibonacci,
= {1, 1, 2,
3, 5, 8,…}, definida por:
Determine a relação para alguns valores crescentes de , e mostre que a relação aproxima-se do limite . O número é designado de proporção áurea e no Maxima está predefinido na constante %phi. - Crie uma função "maximo" que encontre o máximo de todos os números que lhe sejam dados.
Respostas
2. O máximo local encontra-se em (0.709, 4.30), e o mínimo local em (3.29, -4.30).
3.