4. Capacidade
Problema 2
(a) Determine a capacidade de uma esfera condutora isolada, com raio de 4.0 cm, rodeada por ar. (b) A esfera da alínea anterior é coberta com uma camada de vidro de 1 mm de espessura e constante dielétrica de 5.6, deixando um orifício para ligar um cabo à esfera, e a camada de vidro é coberta com uma segunda lâmina metálica esférica de raio 4.1 cm, formando-se assim um condensador esférico. Determine a capacidade desse condensador. (c) Qual a relação entre a capacidade do condensador e a da esfera?
(a) Admitindo que a constante dielétrica do ar é , a capacidade da esfera é:
(b) A capacidade do condensador esférico é:
(c) A relação entre as duas capacidades é igual a
Comentários: O resultado da alínea c mostra a utilidade dos condensadores. A capacidade de armazenar carga do condensador é 230 maior do que uma única esfera. Com um único condutor não é possível obter capacidades elevadas; por exemplo, se a esfera condutora da alínea a fosse do tamanho da Terra (raio de 6371 km), a sua capacidade seria de 7.08×10-4 F. Compare-se essa capacidade com os 3000 F do ultracondensador na figura 4.8 do livro.
Problema 3
No sistema de três condensadores apresentado na figura, µF, µF e µF. A voltagem entre os pontos A e B é de 9.0 V. (a) Determine a carga armazenada em cada condensador. (b) Determine a energia total armazenada no sistema.
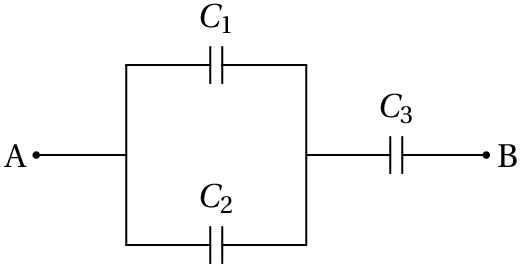
Para resolver este tipo de problema, simplifica-se o circuito até ficar unicamente com um condensador. O primeiro passo é substituir os condensadores de capacidades e , que estão em paralelo, por um condensador equivalente com capacidade . No segundo passo, os condensadores de capacidades e , que ficam ligados em série, são substituídos por um único condensador com capacidade . A figura seguinte mostra esses passos.
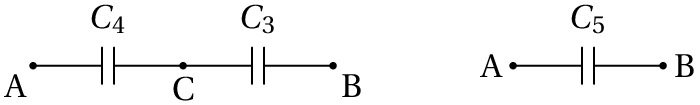
A capacidade do condensador equivalente em paralelo, entre os pontos A e C, é:
E a capacidade do condensador equivalente aos condensadores com capacidades e , em série, é:
(a) Como a diferença de potencial entre os pontos A e B é igual 9 V, a carga armazenada no condensador de capacidade é:
Que é também a carga armazenada nos condensadores de capacidades e , por estarem em série
A diferença de potencial entre os pontos A e C será:
As cargas nos condensadores de capacidades e , que estão ambos ligados entre os pontos A e C, são:
(b) A energia total armazenada no sistema é a soma das energias nos três condensadores, que será igual à energia total armazenada em qualquer um dos outros dois circuitos equivalentes na figura acima. Será então mais fácil determinar essa energia no circuito mais simples, com apenas um condensador de capacidade entre A e B:
Problema 4
Um condensador plano com armaduras de 12 cm2 distanciadas de 1 cm, está totalmente preenchido por dois dielétricos, cada um com espessura igual a 0.5 cm e área igual à das placas. Calcule a capacidade do condensador sabendo que as constantes dos dielétricos são 4.9 e 5.6 (sugestão: admita que o condensador é equivalente a dois condensadores em série, cada um com um dielétrico diferente).
O condensador é equivalente a um condensador plano com armaduras de 12 cm2 a 0.5 cm de distância, com dielétrico de constante 4.9, em série com outro condensador plano com armaduras de 12 cm2 a 0.5 cm de distância e com dielétrico de constante 5.6.
As capacidades desses dois condensadores são:
E a capacidade equivalente dos dois condensadores em série é:
Problema 7
No circuito da figura, calcule a capacidade equivalente: (a) Entre os pontos B e D. (b) Entre os pontos A e B.
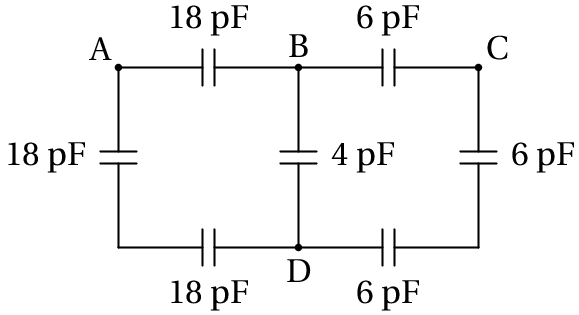
(a) Para determinar a capacidade entre B e D, imagine-se que é ligado entre esses dois pontos um medidor de capacidades, representado por F, na figura seguinte:
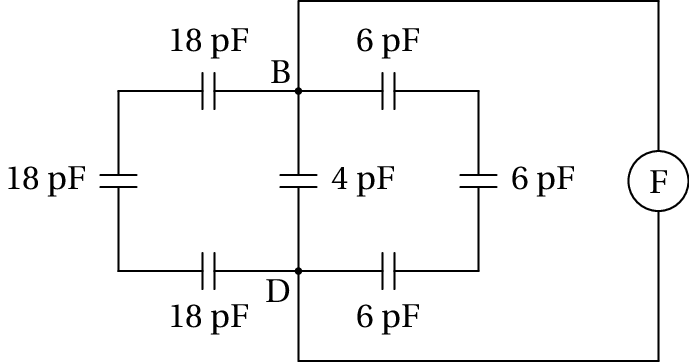
O dispositivo de medição teria de inserir cargas de sinais opostos nos pontos B e D e medir a voltagem devida a essas cargas. As cargas têm 3 percursos alternativos ao entrar nos ponto B e D. Um desses percursos é passando pelos 3 condensadores de 18 pF, que estão em série, e outro dos percursos passa pelos 3 condensadores de 6 pF, também em série. Esses condensadores em série podem ser substituídos pelos condensadores equivalentes com capacidades:
e o circuito fica simplificado da forma seguinte:
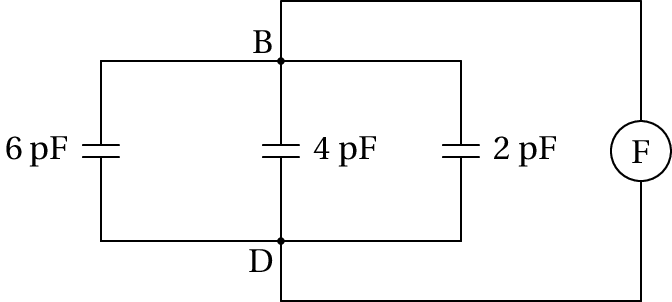
Agora temos 3 condensadores em paralelo, entre os pontos B e D, e a capacidade equivalente é a capacidade do circuito entre os pontos B e D:
(b) Se o medidor de capacidade for ligado entre os pontos A e B, o diagrama é o seguinte:
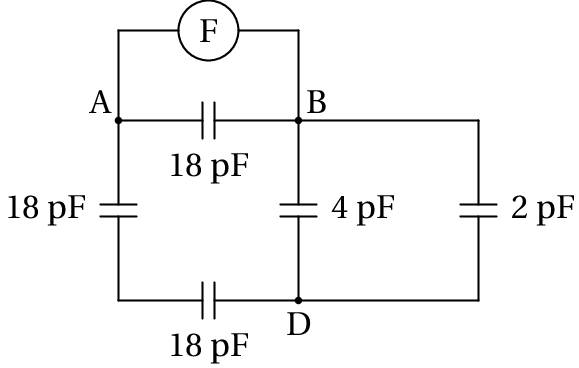
Os condensadores de 4 pF e 2 pF estão em paralelo, entre os pontos B e D, podendo ser substituídos por um único condensador de capacidade 4+2 = 6 pF. O circuito obtido é o seguinte:
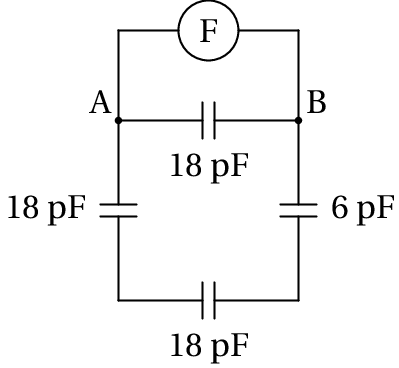
O condensador de 6 pF está agora em série com dois dos condensadores de 18 pF e a capacidade equivalente desse sistema em série é:
e substituindo no diagrama anterior, obtém-se o seguinte circuito equivalente:
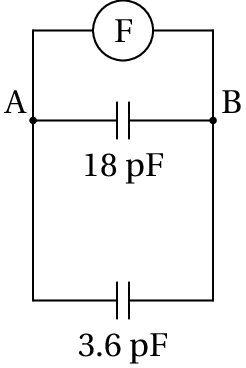
Finalmente, a capacidade entre os pontos A e B e a capacidade equivalente dos condensadores de 18 pF e 3.6 pF em paralelo: