B. Números complexos e fasores

B.1 Números complexos

A forma retangular de um número complexo $z$ é

$$z=x+\mathrm{i}y$$ (B.1)

onde $x$ (parte real) e $y$ (parte imaginária) são dois números reais, no campo dos números reais, $\mathrm{i}$ é a unidade imaginária, $\mathrm{i}=\sqrt{-1}$, e o produto $\mathrm{i}y$ representa um número imaginário. A figura B.1 mostra o chamado plano complexo, que é um plano onde cada ponto corresponde a um número complexo $z$; as suas partes real e imaginária são as projeções $x$ e $y$ em dois eixos perpendiculares, designados por Re (eixo real) e Im (eixo imaginário).

Figura B.1: Número complexo $z=x+\mathrm{i}y$ representado no plano complexo.

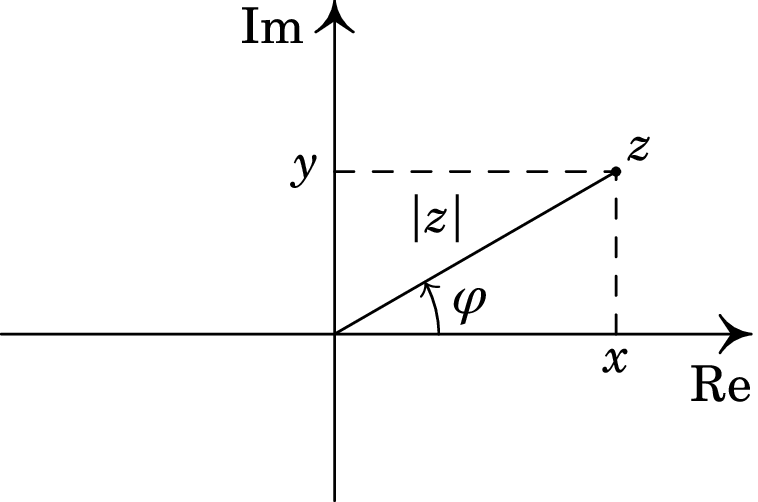
Definem-se o módulo $|z|$ e o argumento $\phi$ do número complexo $z$:

$$|z|=\sqrt{x^2+y^2}\mathit{\hspace{1em}\hspace{1em}}\phi =\mathrm{Arctan}(x,y)$$ (B.2)

onde $\mathrm{Arctan}$ é a função definida em (A.34) e o argumento está no intervalo .

No plano complexo, $|z|$ é a distância desde o ponto onde se encontra $z$ até à origem, e $\phi$ é o ângulo que o segmento desde $z$ até à origem faz com o semieixo Re positivo (ver figura B.1).

Um número complexo $z$ pode então ser escrito também na chamada forma polar projetando as suas partes real e imaginária nos eixos Re e Im:

$$z=|z|\left(\cos \phi +\mathrm{i}\sin \phi \right)$$ (B.3)

A função complexa entre parêntesis na equação (B.3) costuma ser designada por $\mathrm{cis}(\phi )$, ou ainda por ${\mathrm{e}}^{\mathrm{i}\phi }$, por ter propriedades semelhantes à função exponencial real ${\mathrm{e}}^x$. Para mostrar mais facilmente algumas operações entre números complexos, escreveremos a forma polar em algumas das duas notações seguintes:

$$z=|z|{\mathrm{e}}^{\mathrm{i}\phi }\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}z=|z|\mathrm{\angle }\phi$$ (B.4)

A soma de dois números complexos, $z_1=x_1+\mathrm{i}{y}_1$ e $z_2=x_2+\mathrm{i}{y}_2$, é outro número complexo, $z_1+z_2$, com partes real e imaginária iguais à soma das respetivas partes dos dois números:

$$z_1+z_2=\left(x_1+x_2\right)+\mathrm{i}\left(y_1+y_2\right)$$ (B.5)

esta é a mesma forma da soma de dois vetores no plano $xy$, em função das suas componentes. Como tal, a soma de números complexos segue a mesma regra do paralelogramo, no plano complexo, da soma de vetores, como mostra a figura B.2. E a soma de números complexos tem as mesmas propriedades da soma de vetores.

Figura B.2: Adição de números complexos no plano complexo.

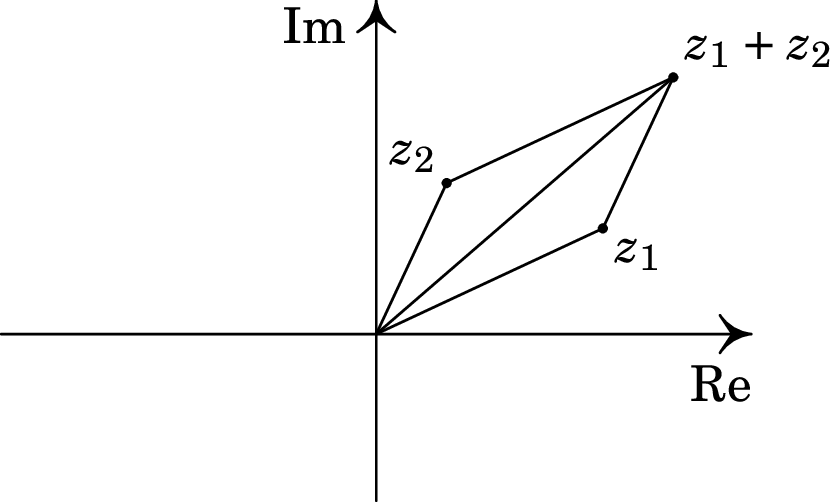
Em contraste com os vetores, no caso dos números complexos é possível definir um produto que dá como resultado um outro número complexo e tem as mesmas propriedades do produto entre números reais (comutatividade, associatividade, distributividade, etc.). O produto entre dois números complexos, $z_1=x_1+\mathrm{i}{y}_1$ e $z_2=x_2+\mathrm{i}{y}_2$, é outro número complexo, $z_1{z}_2$, que pode ser obtido usando a sua propriedade distributiva e o facto de que ${\mathrm{i}}^2=-1$:

$z_1{z}_2$ $=\left(x_1+\mathrm{i}{y}_1\right)\left(x_2+\mathrm{i}{y}_2\right)$

$=x_1{x}_2+{\mathrm{i}}^2{y}_1{y}_2+\mathrm{i}{x}_1{y}_2+\mathrm{i}{x}_2{y}_1$

$=\left(x_1{x}_2-y_1{y}_2\right)+\mathrm{i}\left(x_1{y}_2+x_2{y}_1\right)$ (B.6)

Produto este que tem uma expressão mais simples em termos das componentes polares dos números complexos:

$$z_1{z}_2=|z_1||z_2|{\mathrm{e}}^{\mathrm{i}({\phi }_1+{\phi }_2)}=|z_1||z_2|\mathrm{\angle }({\phi }_1+{\phi }_2)$$ (B.7)

Ou seja, o produto $z_1{z}_2$ tem módulo igual ao produto dos módulos de $z_1$ e $z_2$ e argumento igual à soma dos argumentos de $z_1$ e $z_2$. E a divisão é feita dividindo os módulos e subtraindo os argumentos:

$$\frac{z_1}{z_2}=\frac{|z_1|}{|z_2|}{\mathrm{e}}^{\mathrm{i}({\phi }_1-{\phi }_2)}=\frac{|z_1|}{|z_2|}\mathrm{\angle }({\phi }_1-{\phi }_2)$$ (B.8)

Define-se o conjugado, $z^{*}$, do número $z$, mantendo o módulo igual mas trocando o sinal do argumento:

$$z^{*}=|z|{\mathrm{e}}^{-\mathrm{i}\phi }=|z|\mathrm{\angle }-\phi =x-\mathrm{i}y$$ (B.9)

O produto de um número complexo com o seu conjugado é igual ao seu módulo ao quadrado:

$$z{z}^{*}=z^{*}z={|z|}^2$$ (B.10)

B.2 Fasores

As funções sinusoidais com a forma geral:

$$f(t)=f_{\text{máx}}\cos \left(\omega t+\phi \right)$$ (B.11)

são caraterizadas pela sua amplitude $f_{\text{máx}}$, frequência angular $\omega$ e fase inicial $\phi$.

A forma polar (B.3) de um número complexo mostra que a sua parte real é,

$$\mathrm{Re}(z)=\mathrm{Re}(|z|{\mathrm{e}}^{\mathrm{i}{\phi }_z})=|z|\cos ({\phi }_z)$$ (B.12)

o que sugere uma outra representação para as funções sinusoidais (B.11):

$$f(t)=\mathrm{Re}\left(f_{\text{máx}}{\mathrm{e}}^{\mathrm{i}(\omega t+\phi )}\right)=\mathrm{Re}\left(f_{\text{máx}}{\mathrm{e}}^{\mathrm{i}\phi }{\mathrm{e}}^{\mathrm{i}\omega t}\right)$$ (B.13)

A expressão $f_{\text{máx}}{\mathrm{e}}^{\mathrm{i}\phi }{\mathrm{e}}^{\mathrm{i}\omega t}$ entre parêntesis na equação (B.13) é a representação complexa da função sinusoidal $f(t)$, a qual é uma função real. Quando as funções sinusoidais envolvidas possuem todas a mesma frequência angular $\omega$, então o factor comum ${\mathrm{e}}^{\mathrm{i}\omega t}$ das suas representações complexas pode ser omitido durante os cálculos e reinserido posteriormente. Define-se então o fasor da função $f(t)$ como o número complexo,

$$𝐟=f_{\text{máx}}{\mathrm{e}}^{\mathrm{i}\phi }=f_{\text{máx}}\mathrm{\angle }\phi$$ (B.14)

A relação entre uma função sinusoidal $f(t)$ e o seu fasor $𝐟$ é portanto dada por:

$$f(t)=\mathrm{Re}\left(𝐟{\mathrm{e}}^{\mathrm{i}\omega t}\right)$$ (B.15)

Um fasor é pois uma outra representação de uma função sinusoidal. Apesar de um fasor ser representado como um número complexo, não é um número complexo ordinário, pois possui implicitamente uma dependência temporal. Uma das vantagem de se usarem fasores é que operações tais como a soma, a multiplicação ou divisão por um número complexo, a derivação ou a primitivação de funções sinusoidais são muito mais fáceis de serem efetuadas usando os seus fasores do que usando funções sinusoidais.

Consideremos uma segunda função sinusoidal $g(t)$ com a mesma frequência angular $\omega$ que a função sinuisoidal $f(t)$ da expressão (B.11), mas com valor máximo e argumento diferentes:

$$g(t)=g_{\text{máx}}\cos \left(\omega t+\alpha \right)=\mathrm{Re}\left(𝐠{\mathrm{e}}^{\mathrm{i}\omega t}\right)$$ (B.16)

onde $𝐠=g_{\text{máx}}{\mathrm{e}}^{\mathrm{i}\alpha }=g_{\text{máx}}\mathrm{\angle }\alpha$ é o fasor de $g(t)$.

A soma das funções $f$ e $g$ é então:

$$f(t)+g(t)=\mathrm{Re}\left(𝐟{\mathrm{e}}^{\mathrm{i}\omega t}\right)+\mathrm{Re}\left(𝐠{\mathrm{e}}^{\mathrm{i}\omega t}\right)=\mathrm{Re}\left[\left(𝐟+𝐠\right){\mathrm{e}}^{\mathrm{i}\omega t}\right]$$ (B.17)

onde usámos a propriedade de que a parte real da soma de dois números complexos é igual à soma das suas partes reais (ver expressão (B.5)).

Ou seja, a soma das duas funções sinusoidais com a mesma frequência é também uma função sinusoidal com a mesma frequência angular $\omega$ cujo fasor é igual à soma dos fasores das duas funções, a qual é uma simples soma de números complexos. A maneira mais simples de somar fasores consiste em transformá-los da forma polar para a forma retangular, somar as partes reais e imaginárias, e escrever o fasor da soma na sua forma polar.

Note-se o uso da notação especial para os fasores, $𝐟$, devido a que, apesar de se somarem como números complexos que são, dando outro fasor, o produto complexo entre dois fasores dá um número complexo, mas este já não representa o fasor de nenhuma função sinusoidal.

Contudo, o produto de um fasor por um número complexo ordinário $z=|z|{\mathrm{e}}^{\mathrm{i}{\phi }_z}$ é também um fasor. Considerando o fasor $𝐟$ dado pela expressão (B.14), temos então:

$$z𝐟=|z|f_{\text{máx}}{\mathrm{e}}^{\mathrm{i}(\phi +{\phi }_z)}=|z|f_{\text{máx}}\mathrm{\angle }\left(\phi +{\phi }_z\right)$$ (B.18)

o qual representa a seguinte função sinusoidal:

$h(t)$ $=\mathrm{Re}\left(z𝐟{\mathrm{e}}^{\mathrm{i}\omega t}\right)=|z|f_{\text{máx}}\cos (\omega t+\phi +{\phi }_z)$ (B.19)

O produto de um fasor por um número complexo traduz-se portanto em multiplicar o módulo do fasor pelo módulo desse número complexo e somar ao seu argumento o ângulo desse mesmo número complexo.

A derivada da função $f(t)$ é igual a:

$$f^{\prime }(t)=-\omega f_{\text{máx}}\sin \left(\omega t+\phi \right)$$ (B.20)

a qual pode ser também escrita como:

$$f^{\prime }(t)=\omega f_{\text{máx}}\cos \left(\omega t+\phi +\frac{\pi }{2}\right)$$ (B.21)

que é outra função sinusoidal, com fasor $\omega f_{\text{máx}}\mathrm{\angle }(\phi +\pi /2)$. Isto é, o resultado da derivação de uma função sinusoidal é multiplicar o módulo do seu fasor por $\omega$ e aumentar $\pi /2$ ao seu argumento.

O mesmo resultado pode ser obtido mais facilmente derivando a expressão (B.15). Notando que a derivada da parte real é igual à parte real da derivada, temos que:

$$f^{\prime }(t)=\mathrm{Re}\left({(𝐟{\mathrm{e}}^{\mathrm{i}\omega t})}^{\prime }\right)=\mathrm{Re}\left(\mathrm{i}\omega 𝐟{\mathrm{e}}^{\mathrm{i}\omega t}\right)$$ (B.22)

O qual mostra que o fasor da derivada de $f$ é o fasor de $f$ vezes $\mathrm{i}\omega$:

$$\mathrm{i}\omega 𝐟=\left(\omega \mathrm{\angle }\pi /2\right)\left(f_{\text{máx}}\mathrm{\angle }\phi \right)=\omega f_{\text{máx}}\mathrm{\angle }\left(\phi +\frac{\pi }{2}\right)$$ (B.23)

De forma semelhante, como a primitiva da parte real é igual à parte real da primitiva, a primitiva da expressão (B.15) conduz a:

$$\int f(t)dt=\mathrm{Re}\left(\int 𝐟{\mathrm{e}}^{\mathrm{i}\omega t}dt\right)=\mathrm{Re}\left(\frac{𝐟}{\mathrm{i}\omega }{\mathrm{e}}^{\mathrm{i}\omega t}\right)$$ (B.24)

E conclui-se que o fasor da primitiva de $f$ é o fasor de $f$ dividido por $\mathrm{i}\omega$:

$$\frac{𝐟}{\mathrm{i}\omega }=\frac{f_{\text{máx}}\mathrm{\angle }\phi }{\omega \mathrm{\angle }\pi /2}=\frac{f_{\text{máx}}}{\omega }\mathrm{\angle }\left(\phi -\frac{\pi }{2}\right)$$ (B.25)

Em $t=0$, a expressão (B.15) mostra que $f(0)=\mathrm{Re}(𝐟)$. Já em $t>0$, ${\mathrm{e}}^{\mathrm{i}\omega t}=1\mathrm{\angle }\omega t$ é um número complexo com módulo unitário e argumento $\omega t$ que aumenta diretamente proporcional ao tempo. O produto do fasor por ${\mathrm{e}}^{\mathrm{i}\omega t}$ deixa o seu módulo igual mas faz rodar o seu argumento em $\omega t$, no sentido positivo (do eixo Re para o eixo Im). Como tal, o fasor roda no plano complexo, com velocidade angular $\omega$ constante e a cada instante $t$ o valor da função $f$ é a projeção do fasor, após rodar, no eixo Re. O lado esquerdo da figura B.3 mostra a representação do fasor $𝐟$, como um vetor no plano complexo, e o lado direito mostra o fasor multiplicado por ${\mathrm{e}}^{\mathrm{i}\omega t}$, em quatro instantes: $t_0=0$, $t_1=T/4$, $t_2=T/2$ e $t_3=3T/2$, em que $T=2\pi /\omega$ é o seu período de rotação (em cada intervalo $T/4$ o vetor roda $\omega T/4=\pi /2$ radianos).

Figura B.3: Fasor $𝐟$ no plano complexo (esquerda) e valores de $f(t)$ em 4 instantes (direita).

Os valores da função $f(t)$ nos quatro instantes $t_0$, $t_1$, $t_2$ e $t_3$ são as quatro coordenadas $f_0$, $f_1$, $f_2$ e $f_3$ do vetor no eixo real. Os fasores são vetores que rodam no plano complexo, em função do tempo; os fasores de funções sinusoidais com a mesma frequência rodam com a mesma velocidade angular e, portanto, a soma deles também roda com a mesma frequência.