8. Cálculo do campo magnético

Problema 8.1

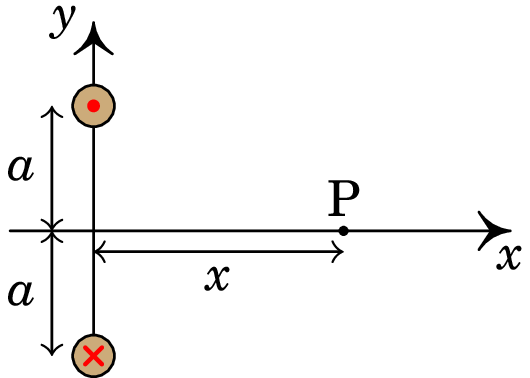
A figura mostra dois fios compridos e paralelos, no plano perpendicular a eles. A intensidade da corrente em cada fio é a mesma, $I$, mas com sentidos opostos, como indicam o ponto e o x nos dois fios.
(a) Represente graficamente os vetores de campo magnético devido a cada fio e o campo magnético resultante no ponto P.
(b) Encontre a expressão do módulo do campo magnético em qualquer ponto P sobre o eixo $x$, em função da distância $x$ de P à origem.

Resolução. (a) No plano $xy$, as linhas do campo ${\overrightarrow{B}}_1$ devido a fio de cima são circunferências com centro no fio, no sentido contrário aos ponteiros do relógio. No ponto P, o vetor ${\overrightarrow{B}}_1$ é perpendicular ao segmento entre P e o fio, no sentido indicado na figura seguinte. As linhas do campo devido ao fio de baixo rodam no sentido dos ponteiros do relógio e no ponto P o campo ${\overrightarrow{B}}_2$ é perpendicular ao segmento entre P e esse fio, como mostra a figura:

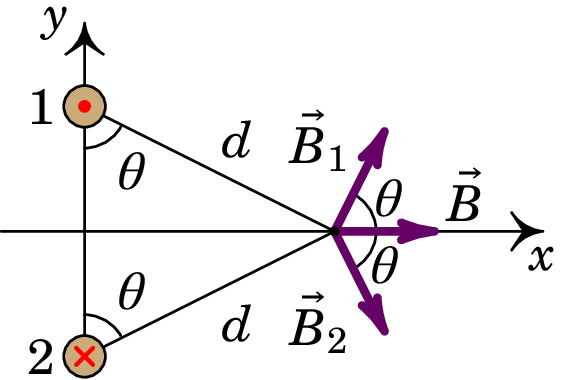
Como os dois fios estão à mesma distância do ponto P, e transportam correntes com a mesma intensidade, os módulos de ${\overrightarrow{B}}_1$ e ${\overrightarrow{B}}_2$ são iguais. E como o ângulo que cada um desses vetores faz com o eixo dos $x$ é o mesmo, o campo resultante em P, $\overrightarrow{B}={\overrightarrow{B}}_1+{\overrightarrow{B}}_2$, será no sentido positivo do eixo dos $x$, tal como mostra a figura acima.

(b) Os módulos dos dois campos no ponto P são:

$$B_1=B_2=\frac{2k_{\mathrm{m}}I}{d}$$

O campo resultante, $\overrightarrow{B}=B\hat{ı}$, no sentido positivo do eixo dos $x$, tem módulo $B$ igual à soma das componentes $x$ de ${\overrightarrow{B}}_1$ e ${\overrightarrow{B}}_2$

$$B=2B_1\cos \theta =\frac{4k_{\mathrm{m}}I}{d}\cos \theta =\frac{4k_{\mathrm{m}}Ia}{d^2}=\frac{4k_{\mathrm{m}}Ia}{x^2+a^2}$$

Problema 8.2

Considere o fio representado na figura, composto por dois segmentos semicirculares concêntricos de raios $R_1$ e $R_2$, percorrido por uma corrente de intensidade $I$. Determine o campo magnético no centro P dos dois segmentos semicirculares.

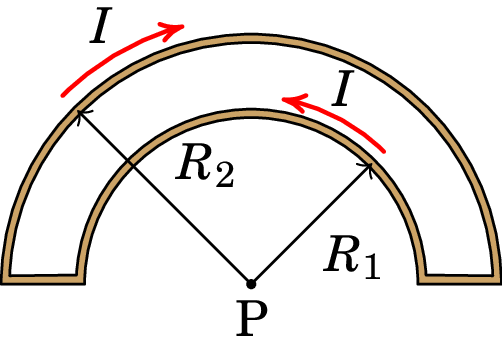
Resolução. Com plano $xy$ no plano do fio e origem no ponto P, o vetor posição $\overrightarrow{r}$ do ponto P é nulo. Nos dois segmentos retilíneos o vetor posição ${\overrightarrow{r}}^{\prime }$ de um ponto no segmento é na mesma direção da corrente e, como tal,

$$\overrightarrow{I}\times \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)=\overrightarrow{0}$$

No segmento semicircular de raio $R_1$, o vetor ${\overrightarrow{r}}^{\prime }$ é perpendicular à corrente $\overrightarrow{I}$ e, usando a regra da mão direita obtém-se:

$$\overrightarrow{I}\times \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)=I|{\overrightarrow{r}}^{\prime }|\hat{k}=I{R}_1\hat{k}$$

O campo magnético produzido por esse segmento, no ponto P, calcula-se a partir da lei de Biot-Savart:

$$\overrightarrow{B}=k_{\mathrm{m}}{\int }_0^{\pi }\frac{\overrightarrow{I}\times \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)}{{\left|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right|}^3}{R}_{1}d\varphi =\frac{\pi k_{\mathrm{m}}I}{R_1}\hat{k}$$

No segmento semicircular de raio $R_2$, o vetor ${\overrightarrow{r}}^{\prime }$ também é perpendicular à corrente $\overrightarrow{I}$, mas a regra da mão direita conduz a um vetor oposto a $\hat{k}$:

$$\overrightarrow{I}\times \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)=-I|{\overrightarrow{r}}^{\prime }|\hat{k}=-I{R}_2\hat{k}$$

E o campo magnético produzido por esse segmento, no ponto P, é igual a:

$$\overrightarrow{B}=k_{\mathrm{m}}{\int }_0^{\pi }\frac{\overrightarrow{I}\times \left(\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right)}{{\left|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }\right|}^3}{R}_{2}d\varphi =-\frac{\pi k_{\mathrm{m}}I}{R_2}\hat{k}$$

O campo total é a soma vetorial dos campos dos dois segmentos semicirculares:

$$\overrightarrow{B}=\pi k_{\mathrm{m}}I\left(\frac{1}{R_1}-\frac{1}{R_2}\right)\hat{k}$$

em que o versor $\hat{k}$ aponta para fora da folha.

Problema 8.3

A figura mostra uma bobina de Helmholtz, formada por duas bobinas circulares, cada uma de raio $R$ e com $N$ espiras, ambas com eixo no eixo $z$, paralelas e a uma distância $R$ entre elas. A corrente $I$ é igual nas duas bobinas e circula no mesmo sentido em ambas. Com essa configuração é possível produzir campo magnético aproximadamente constante na região central entre as duas bobinas.

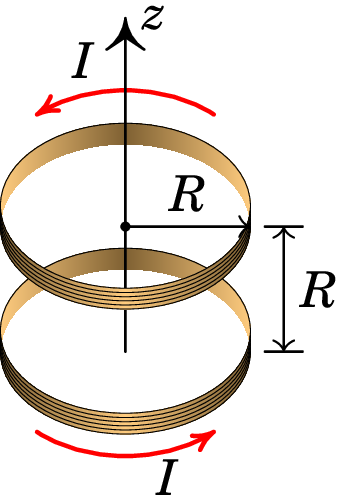
(a) Encontre a expressão $B(z)$ do módulo do campo magnético em função de $z$, com $z=0$ no ponto médio entre os centros das duas bobinas.
(b) Mostre que as duas primeiras derivadas de $B(z)$ são nulas em $z=0$.
(c) Mostre que os três primeiros termos na série de Taylor de $B(z)$ em torno de $z=0$ conduzem a um valor constante.

Resolução. (a) O módulo do campo magnético de cada bobina ao longo do eixo $z$, calculado no exemplo 8.3 do livro, é:

$$\frac{2\pi k_{\mathrm{m}}NI{R}^2}{{\left(d^2+R^2\right)}^{3/2}}$$

onde $d$ é a distância desde o centro da bobina. Na bobina de cima $d=z-R/2$ e na bobina de baixo $d=z+R/2$. Como os campos das duas bobinas são ambos no sentido positivo do eixo $z$, o campo total é também nessa direção e tem módulo:

$$B(z)=\frac{2\pi k_{\mathrm{m}}NI{R}^2}{{\left({(z-\frac{R}{2})}^2+R^2\right)}^{3/2}}+\frac{2\pi k_{\mathrm{m}}NI{R}^2}{{\left({(z+\frac{R}{2})}^2+R^2\right)}^{3/2}}$$

(b) Derivando $B(z)$ obtém-se:

$$\frac{\mathrm{d}B}{\mathrm{d}z}=-\frac{6\pi k_{\mathrm{m}}NI{R}^2(z-\frac{R}{2})}{{\left({(z-\frac{R}{2})}^2+R^2\right)}^{5/2}}-\frac{6\pi k_{\mathrm{m}}NI{R}^2(z+\frac{R}{2})}{{\left({(z+\frac{R}{2})}^2+R^2\right)}^{5/2}}$$

e em $z=0$ o resultado é:

$${\frac{\mathrm{d}B}{\mathrm{d}z}|}_0=\frac{3\pi k_{\mathrm{m}}NI{R}^3}{{\left(\frac{R^2}{4}+R^2\right)}^{5/2}}-\frac{3\pi k_{\mathrm{m}}NI{R}^3}{{\left(\frac{R^2}{4}+R^2\right)}^{5/2}}=0$$

A segunda derivada é:

${\displaystyle \frac{{\mathrm{d}}^{2}B}{\mathrm{d}{z}^2}}=$ $-{\displaystyle \frac{6\pi k_{\mathrm{m}}NI{R}^2}{{\left({(z-\frac{R}{2})}^2+R^2\right)}^{5/2}}}-{\displaystyle \frac{6\pi k_{\mathrm{m}}NI{R}^2}{{\left({(z+\frac{R}{2})}^2+R^2\right)}^{5/2}}}$

$+{\displaystyle \frac{30\pi k_{\mathrm{m}}NI{R}^2{(z-\frac{R}{2})}^2}{{\left({(z-\frac{R}{2})}^2+R^2\right)}^{7/2}}}+{\displaystyle \frac{30\pi k_{\mathrm{m}}NI{R}^2{(z+\frac{R}{2})}^2}{{\left({(z+\frac{R}{2})}^2+R^2\right)}^{7/2}}}$

e em $z=0$ o resultado é:

${{\displaystyle \frac{{\mathrm{d}}^{2}B}{\mathrm{d}{z}^2}}|}_0$ $=-{\displaystyle \frac{12\pi k_{\mathrm{m}}NI{R}^2}{{\left(\frac{R^2}{4}+R^2\right)}^{5/2}}}+{\displaystyle \frac{15\pi k_{\mathrm{m}}NI{R}^4}{{\left(\frac{R^2}{4}+R^2\right)}^{7/2}}}$

$=-{\displaystyle \frac{384\pi k_{\mathrm{m}}NI}{5^{5/2}{R}^3}}+{\displaystyle \frac{1920\pi k_{\mathrm{m}}NI}{5^{7/2}{R}^3}}=0$

(c) Os três primeiros termos na série de Taylor de $B(z)$ em torno de $z=0$ são:

$$B(z)=B(0)+{\frac{\mathrm{d}B}{\mathrm{d}z}|}_{0}z+{\frac{{\mathrm{d}}^{2}B}{\mathrm{d}{z}^2}|}_0{z}^2$$

e usando os resultados das alíneas anteriores obtém-se:

$$B(z)=\frac{32\pi k_{\mathrm{m}}NI}{5^{3/2}R}$$

que não depende de $z$.

Problema 8.4

Um condutor cilíndrico oco, com raio interno $a$ e raio externo $b$ transporta uma corrente $I$, paralela ao eixo do condutor, distribuída uniformemente na secção transversal do condutor. Encontre a expressão do campo magnético em função da distância até ao eixo do cilindro, $\varrho$.

Resolução. A figura mostra a secção transversal do condutor. As linhas de campo magnético serão circunferências perpendiculares ao eixo do condutor e com centro nele; a curva C na figura é uma dessas linhas de campo, de raio $\varrho$ entre 0 e $\mathrm{\infty }$.

A área da secção transversal do condutor é $\pi (b^2-a^2)$, e como a corrente está distribuída uniformemente, a densidade de corrente é constante e com módulo igual a:

$$J=\frac{I}{\pi (b^2-a^2)}$$

o integral de linha do campo magnético, ao longo da curva C na figura, é:

$${\oint }_{\mathrm{C}}\overrightarrow{B}\cdot d\overrightarrow{r}=B\int ds=2\pi \varrho B$$

E usando a lei de Ampère,

$${\oint }_{\mathrm{C}}\overrightarrow{B}\cdot d\overrightarrow{r}=4\pi k_{\mathrm{m}}{I}_{\mathrm{C}}$$

concluímos que:

$$B=\frac{2k_{\mathrm{m}}{I}_{\mathrm{C}}}{\varrho }$$

Se o raio do círculo for menor que $a$, a corrente interna $I_{\mathrm{C}}$ e o campo magnético serão nulos:

se $\varrho >b$, a corrente interna será igual à corrente total $I$ e o campo magnético será:

$$\overrightarrow{B}=\frac{2k_{\mathrm{m}}I}{\varrho }\hat{\varphi }\mathit{\hspace{1em}\hspace{1em}}(\varrho >b)$$

onde $\hat{\varphi }$ é o versor azimutal num sistema de coordenadas cilíndricas em que $\hat{k}$ aponta na direção e sentido da corrente. Finalmente, dentro do condutor ($a\le \varrho \le b$) a corrente interna calcula-se multiplicando a área da parte da secção do condutor dentro do círculo, $\pi ({\varrho }^2-a^2)$, vezes a densidade da corrente. O resultado obtido é:

$$\overrightarrow{B}=\frac{2k_{\mathrm{m}}I}{\varrho }\left(\frac{{\varrho }^2-a^2}{b^2-a^2}\right)\hat{\varphi }\mathit{\hspace{1em}}(a\le \varrho \le b)$$

Problema 8.5

Um fio condutor cilíndrico muito comprido, de raio $a$, conduz corrente de intensidade $I$. A corrente está distribuída de forma não-uniforme, com $J=A{\varrho }^3$, onde $\varrho$ é a distância até o eixo do fio e $A$ uma constante. Determine a expressão do campo magnético no interior e no exterior do fio.

Resolução. Escolhendo o eixo $z$ no eixo do cilindro, no sentido da corrente, e como a densidade de corrente depende unicamente da distância ao eixo, existe simetria cilíndrica e as linhas de campo magnético serão circunferências perpendiculares ao cilindro e com centro no eixo dos $z$. O integral de linha do campo $\overrightarrow{B}$, ao longo de uma linha de campo magnético de raio $\varrho$ é:

$${\oint }_{\mathrm{C}}\overrightarrow{B}\cdot d\overrightarrow{r}=B\oint ds=2\pi \varrho B$$

E usando a lei de Ampère, obtemos

$${\oint }_{\mathrm{C}}\overrightarrow{B}\cdot d\overrightarrow{r}=4\pi k_{\mathrm{m}}{I}_{\mathrm{C}}$$

Comparando as duas equações anteriores, conclui-se que:

$$B=\frac{2k_{\mathrm{m}}{I}_{\mathrm{C}}}{\varrho }$$

Se $\varrho$ for menor que o raio do cilindro, a corrente através de C será:

$$I_{\mathrm{C}}=\iint JdA=A{\int }_0^{2\pi }{\int }_0^{\varrho }{r}^{4}drd\varphi =\frac{2}{5}\pi A{\varrho }^5$$

Se $\varrho$ for maior do que o raio do cilindro, o integral de $J$ é no intervalo $0\le r\le a$ e no resultado anterior basta substituir $\varrho$ por $a$:

$$I_{\mathrm{C}}=\frac{2}{5}\pi A{a}^5=I$$

Como tal, a constante $A$ é igual a:

$$A=\frac{5I}{2\pi a^5}$$

e o módulo do campo magnético é:

O campo $\overrightarrow{B}$ é na direção azimutal $\hat{\varphi }$.

Problema 8.6

A figura representa três fios condutores retilíneos, muito compridos e paralelos ao eixo $z$, com correntes no sentido positivo desse eixo. O primeiro fio passa pelo ponto ($x$, $y$) = (0, 1 cm) e tem corrente de 0.64 A, o segundo fio passa pelo pela origem e tem corrente de 0.63 A e o terceiro fio passa pelo ponto ($x$, $y$) = (2 cm, 0) e tem corrente de 0.43 A. Calcule o módulo da força magnética resultante, por unidade de comprimento, no fio que passa pela origem.

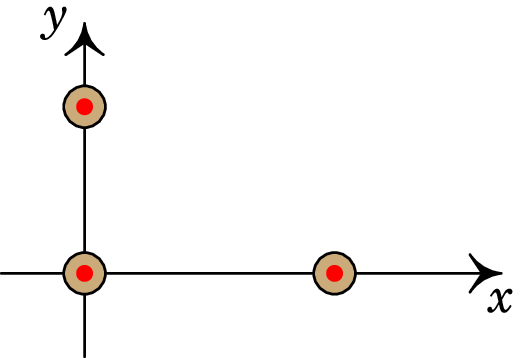
Resolução. Ambos fios produzem forças atrativas no fio que passa pela origem. Em unidades SI, a força produzida pelo fio que passa pelo ponto (0, 1 cm), por unidade de comprimento, é igual a:

$$\frac{{\overrightarrow{F}}_1}{l}=\frac{2\times {10}^{-7}\times 0.64\times 0.63}{0.01}\hat{ȷ}=8.064\times {10}^{-6}\hat{ȷ}$$

E o fio que passa pelo ponto (2 cm, 0) produz força por unidade de comprimento igual a:

$$\frac{{\overrightarrow{F}}_2}{l}=\frac{2\times {10}^{-7}\times 0.43\times 0.63}{0.02}\hat{ı}=2.709\times {10}^{-6}\hat{ı}$$

A força resultante sobre o fio na origem, por unidade de comprimento, é então:

$$\frac{\overrightarrow{F}}{l}=2.709\times {10}^{-6}\hat{ı}+8.064\times {10}^{-6}\hat{ȷ}$$

O módulo da força, por unidade de comprimento, é igual a:

$$\frac{F}{l}=\sqrt{{2.709}^2+8.064}\times {10}^{-6}=8.507\frac{\mu \mathrm{N}}{\mathrm{m}}$$

Problema 8.7

Considere dois fios de cobre, retilíneos e paralelos, de 60 cm de comprimento, distanciados de 9 cm e com raios de 2 mm e 3 mm. Calcule o valor da força magnética entre os fios quando cada um deles for ligado a uma f.e.m. de 1.5 V. (Use o valor da resistividade do cobre à temperatura ambiente: 17 n$\mathrm{\Omega }$·m.)

Resolução. As resistências dos fios, $R_1$ e $R_2$, calculam-se multiplicando a resistividade do cobre pelo comprimento do fio, dividido pela área da secção transversal do fio (unidades SI):

$R_1$ $={\displaystyle \frac{\rho L_1}{\pi r_1^2}}={\displaystyle \frac{17\times {10}^{-9}\times 0.6}{\pi \times {0.002}^2}}=8.117\times {10}^{-4}\mathrm{\Omega }$

$R_2$ $={\displaystyle \frac{\rho L_2}{\pi r_2^2}}={\displaystyle \frac{17\times {10}^{-9}\times 0.6}{\pi \times {0.003}^2}}=3.608\times {10}^{-4}\mathrm{\Omega }$

A corrente em cada fio é igual à diferença de potencial sobre a resistência do fio:

$I_1$ $={\displaystyle \frac{\mathrm{\Delta }V}{R_1}}=={\displaystyle \frac{1.5}{8.117\times {10}^{-4}}}=1848\mathrm{A}$

$I_2$ $={\displaystyle \frac{\mathrm{\Delta }V}{R_2}}={\displaystyle \frac{1.5}{3.608\times {10}^{-4}}}=4158\mathrm{A}$

O módulo da força magnética entre os dois fios é:

$$F=\frac{k_{\mathrm{m}}{I}_1{I}_{2}L}{d}=\frac{2\times {10}^{-7}\times 0.6\times 1848\times 4158}{0.09}=10.25\mathrm{N}$$

Comentários: A diferença de potencial de 1.5 V em cada fio conduz a correntes de milhares de ampere, que queimavam um fio de apenas uns poucos milímetros de raio. Se fosse usada uma pilha de 1.5 V, a resistência interna provavelmente seria maior do que a resistência de cada fio; como tal, a diferença de potencial no fio seria muito menor do que 1.5 V e a própria pilha aqueceria com o fio. Para realizar esse tipo de experiências para medir a força magnética entre dois fios de cobre, costuma ligar-se uma resistência em série para reduzir a intensidade da corrente, e a força magnética a medir será muito menor.

Problema 8.8

A figura mostra as linhas de campo magnético de um fio com corrente, dentro de um campo magnético externo uniforme ${\overrightarrow{B}}_{\text{ext}}$; o fio é perpendicular à folha e os eixos $y$ e $z$ foram escolhidos sobre o plano da folha.
(a) Escreva o versor na direção do campo externo, usando o sistema de eixos dado.
(b) Escreva o versor direção da corrente no fio.
(c) Calcule e represente o vetor unitário na direção da força sobre o fio.
(d) Considerando que $I=0.5$ A e se a força sobre o fio, por unidade de comprimento, for de $2\times {10}^{-5}$ N/m, calcule a distância desde o fio até o ponto P.

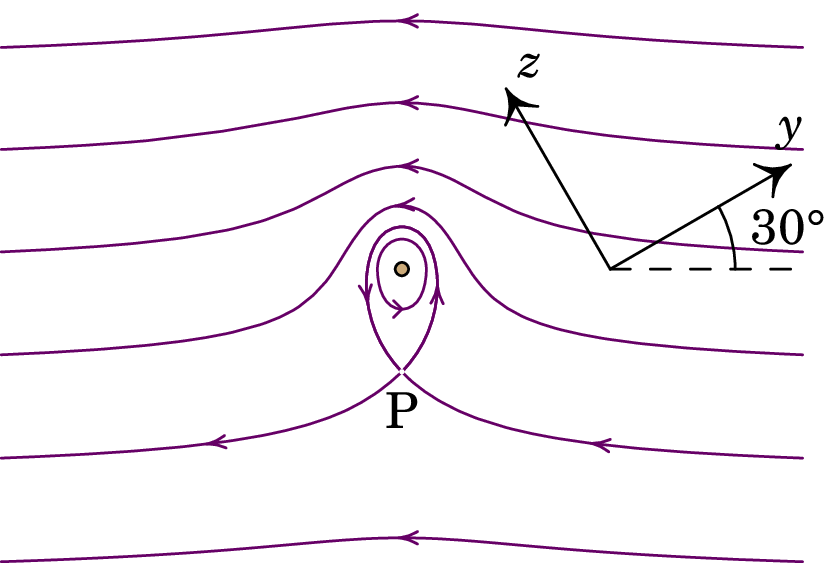
Resolução. (a) O campo externo aponta da direita para a esquerda, que no sistema de eixos $yz$ é:

$${\hat{B}}_{\text{ext}}=-\cos {30}^{\circ }\hat{ȷ}+\sin {30}^{\circ }\hat{k}=\frac{1}{2}\left(-\sqrt{3}\hat{ȷ}+\hat{k}\right)$$

(b) Na vizinhança do fio, as linhas de campo rodam no sentido contrário dos ponteiros do relógio, indicando que a corrente do fio é para cá da folha, ou seja, na direção de $\hat{ȷ}\times \hat{k}$ que é o versor $\hat{ı}$.

(c) A direção e sentido da força é a mesma de $\overrightarrow{I}\times {\overrightarrow{B}}_{\text{ext}}$, ou seja,

$$\hat{ı}\times {\hat{B}}_{\text{ext}}=\frac{1}{2}\hat{ı}\times \left(-\sqrt{3}\hat{ȷ}+\hat{k}\right)=\frac{1}{2}\left(-\hat{ȷ}-\sqrt{3}\hat{k}\right)$$

Não é necessário dividir pelo módulo do vetor, porque este vetor já tem módulo unitário. Observe-se que a direção e sentido da força é de cima para baixo na figura.

(d) A força magnética sobre o fio é produzida pelo campo externo $B_{\text{ext}}$. Usando a expressão para a força magnética sobre o fio por unidade de comprimento, $F/L$, obtém-se o módulo do campo externo (unidades SI):

$$\frac{F}{L}=I{B}_{\text{ext}}\mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}2\times {10}^{-5}=0.5B_{\text{ext}}\mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}{B}_{\text{ext}}=4\times {10}^{-5}$$

No ponto P, o campo produzido pelo fio tem o mesmo módulo do campo externo. Igualando à expressão para o módulo do campo produzido pelo fio no ponto P ao módulo do campo externo, encontra-se a distância d (unidades SI):

$$\frac{2k_{\mathrm{m}}I}{d}=B_{\text{ext}}\mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}d=\frac{2k_{\mathrm{m}}I}{B_{\text{ext}}}=\frac{{10}^{-7}}{4\times {10}^{-5}}=2.5\times {10}^{-3}$$

O ponto P encontra-se a 2.5 mm do fio.