10. Circuitos de corrente alternada

Jaime E. Villate e Luís Miguel Martelo

(31 de agosto de 2025)

Problema 10.1

A resistência de uma bobina é 150 $\Omega$ e a sua indutância é 1.4 H. A bobina é ligada à rede elétrica com tensão máxima 325 V e frequência de 50 Hz. Encontre a expressão para a corrente na bobina em função do tempo $t$ .

Resolução. Usaremos unidades SI. A frequência angular da tensão e da corrente é

\omega=2\,\pi\,f=100\,\pi\approx 314.16\,\mathrm{Hz\,\,(ou\,rad/s)}

A bobina é considerada como uma resistência em série com um indutor. Como tal, a sua impedância é a soma das impedâncias da resistência e do indutor:

	$\displaystyle Z$	$\displaystyle=R+\mathrm{i}\omega L=150+\mathrm{i}\,1.4\times 314.16$
		$\displaystyle=\sqrt{150^{2}+439.824^{2}}\,\angle\,\arctan\left(\dfrac{439.824}% {150}\right)=464.7\,\angle\,1.242\,\,\Omega$

Admitindo que a tensão da rede elétrica em função do tempo seja $325\,\cos(\omega\,t)$ , a voltagem máxima na bobina é 325 V, com fase $\varphi_{V}=0$ . A corrente máxima e o desfasamento da corrente na bobina são:

I_{\text{m\'{a}x}}=\dfrac{V_{\text{m\'{a}x}}}{|Z|}=\dfrac{325}{464.7}=0.6694\,% \mathrm{A}\qquad\qquad\varphi_{I}=\varphi_{V}-\varphi_{Z}=-1.242\,\mathrm{rad}

E a expressão para a corrente é

I(t)=0.6694\,\cos(314.16\,t-1.242)\,\,(\mathrm{A})

Problema 10.2

Nos dois circuitos representados na figura, calcule a corrente e a tensão em todos os elementos do circuito.

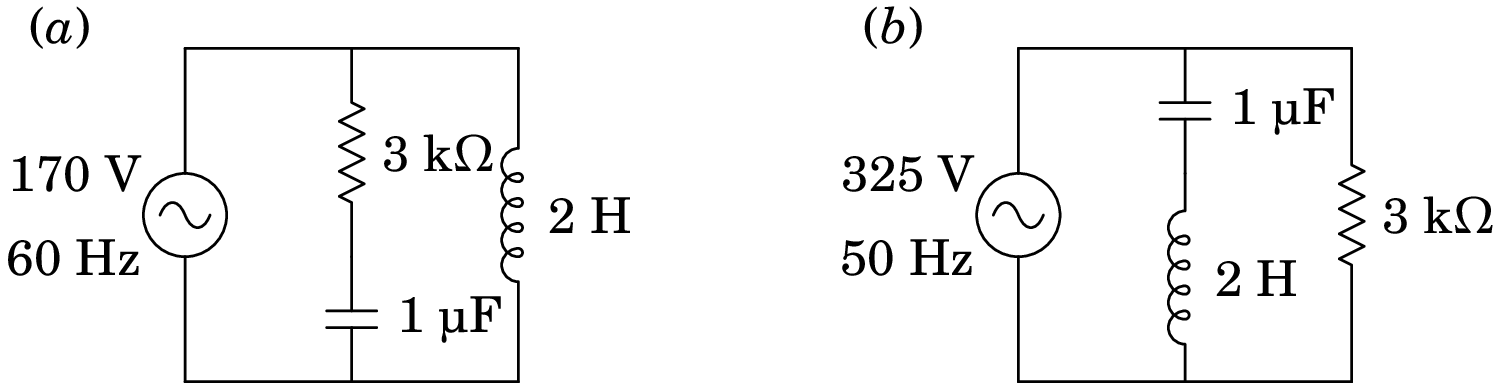
Resolução. (a) Usando unidades de V para as voltagens e k $\Omega$ para as impedâncias (o que implica que a unidade da corrente elétrica será mA) e kHz para as frequências (pelo que a unidade do tempo será ms, H a das indutâncias e µF a das capacidades), a frequência angular da fonte e as impedâncias dos 3 elementos no circuito são as seguintes:

	$\displaystyle\omega$	$\displaystyle=\dfrac{2\pi\times 60}{1000}=\dfrac{3\pi}{25}\,\,\,\,\mathrm{kHz}% \,({\mathrm{ou\,krad/s)}}$
	$\displaystyle Z_{R}$	$\displaystyle=R=3=3\angle\,0\,\,\,\,\mathrm{k}\Omega$
	$\displaystyle Z_{C}$	$\displaystyle=\dfrac{1}{\mathrm{i}\,\omega\,C}=-\dfrac{\mathrm{i}\,25}{3\pi}=% \dfrac{25}{3\pi}\angle\,{-\pi/2}\,\,\,\,\mathrm{k}\Omega$
	$\displaystyle Z_{L}$	$\displaystyle=\mathrm{i}\,\omega\,L=\dfrac{\mathrm{i}\,6\pi}{25}=\dfrac{6\pi}{% 25}\angle\,{\pi/2}\,\,\,\,\mathrm{k}\Omega$

Considerando que a fase inicial da voltagem alternada nos terminais da fonte é nula, a sua expressão em função do tempo é dada por

\varepsilon(t)=\varepsilon_{\text{m\'{a}x}}\cos(\omega\,t)=170\,\cos\left(% \dfrac{3\,\pi}{25}\,t\right)

à qual corresponde o fasor: ${\boldsymbol{\varepsilon}}=170\,\angle\,0$ . No indutor, a voltagem é a mesma voltagem da fonte:

\mathbf{V}_{L}=\boldsymbol{\varepsilon}=170\,\angle\,0

e a expressão da voltagem no indutor em função do tempo, $V_{L}(t)$ , é a mesma expressão $\varepsilon(t)$ acima. Usando a relação $\mathbf{V}_{L}=Z_{L}\mathbf{I}_{L}$ , o fasor da corrente no indutor é,

\mathbf{I}_{L}=\dfrac{{\mathbf{V}}_{L}}{Z_{L}}=\dfrac{170\,\angle\,0}{\dfrac{6% \pi}{25}\angle\,{\pi/2}}=225.5\,\angle-\dfrac{\pi}{2}

ao qual corresponde a função:

I_{L}(t)=225.5\,\cos\left(\dfrac{3\pi}{25}t-\dfrac{\pi}{2}\right)=225.5\,\sin% \left(\dfrac{3\pi}{25}t\right)

A voltagem no ramo da resistência em série com o condensador é igual à voltagem da fonte; como tal, o fasor da corrente nesse ramo é:

\mathbf{I}_{R}=\mathbf{I}_{C}=\dfrac{\boldsymbol{\varepsilon}}{Z_{R}+Z_{C}}=% \dfrac{170\,\angle\,0}{3-\dfrac{\mathrm{i}\,25}{3\pi}}=42.45\,\angle\,0.724

onde se usou:

Z_{R}+Z_{C}=3-\dfrac{\mathrm{i}\,25}{3\pi}=\sqrt{3^{2}+\left(\dfrac{25}{3\pi}% \right)^{2}}\,\angle\,\arctan\left(\dfrac{25/(3\pi)}{3}\right)=4.00452\,\angle% \,-0.724

A expressão da corrente comum à resistência e ao condensador em função do tempo é então:

I_{R}(t)=I_{C}(t)=42.45\,\cos\left(\dfrac{3\pi}{25}\,t+0.724\right)

Os fasores das voltagens na resistência e no condensador são então,

	$\displaystyle\mathbf{V}_{R}$	$\displaystyle=Z_{R}\mathbf{I}_{R}=127.4\,\angle\,0.724$
	$\displaystyle\mathbf{V}_{C}$	$\displaystyle=Z_{C}\mathbf{I}_{R}=112.6\,\angle\,-0.8468$

e as voltagens em função do tempo são:

	$\displaystyle V_{R}(t)$	$\displaystyle=127.4\,\cos\left(\dfrac{3\,\pi}{25}\,t+0.724\right)$
	$\displaystyle V_{C}(t)$	$\displaystyle=112.6\,\cos\left(\dfrac{3\,\pi}{25}\,t-0.8468\right)$

(b) Segue-se o mesmo procedimento da alínea (a), mas com os novos valores de frequência e voltagem máxima da fonte e tendo em conta que agora o condensador o indutor estão em série, e a sua combinação está em paralelo com a resistência. A frequência angular é agora: $\omega=\pi/10$ .

Z_{C}=\dfrac{1}{\mathrm{i}\,\omega}=-\dfrac{\mathrm{i}\,10}{\pi}\qquad Z_{L}=% \mathrm{i}\,2\omega=\dfrac{\mathrm{i}\,\pi}{5}\qquad Z_{R}=3

	$\displaystyle\mathbf{I}_{C}$	$\displaystyle=\dfrac{325}{Z_{C}+Z_{L}}=127.2\,\angle\,\dfrac{\pi}{2}$
	$\displaystyle\mathbf{V}_{C}$	$\displaystyle=Z_{C}\mathbf{I}_{C}=404.9$
	$\displaystyle\mathbf{V}_{L}$	$\displaystyle=Z_{L}\mathbf{I}_{C}=79.93\,\angle\,\pi$
	$\displaystyle\mathbf{I}_{R}$	$\displaystyle=\dfrac{325}{Z_{R}}=108.3$

Como tal, a corrente e a voltagem no condensador são:

I_{C}=-127.2\,\sin\left(\dfrac{\pi}{10}\,t\right)\quad V_{C}=404.9\,\cos\left(% \dfrac{\pi}{10}\,t\right)

No indutor:

I_{L}=-127.2\,\sin\left(\dfrac{\pi}{10}\,t\right)\quad V_{L}=-79.93\,\cos\left% (\dfrac{\pi}{10}\,t\right)

E na resistência:

I_{R}=108.3\,\cos\left(\dfrac{\pi}{10}\,t\right)\quad V_{R}=325\,\cos\left(% \dfrac{\pi}{10}\,t\right)

Problema 10.3

A figura mostra um filtro rejeita-banda que atenua as frequências angulares próximas de 1 kHz.

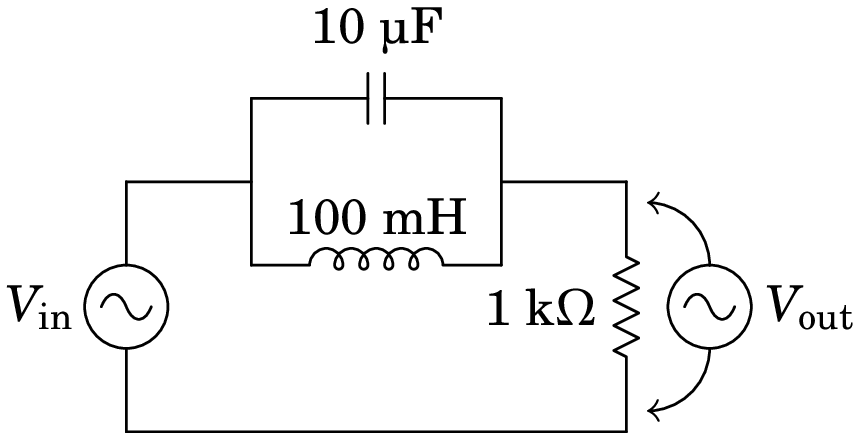
(a) Determine a função de resposta em frequência, $\mathcal{R}$ , do circuito.
(b) Mostre que para $\omega=1$ kHz, $\mathcal{R}$ é igual a zero.
(c) Calcule o módulo de $\mathcal{R}$ e trace o seu gráfico para $\omega$ entre 0 e 2 kHz.

Resolução. (a) Usando unidades de k $\Omega$ para as impedâncias, H para a indutância, µF para a capacidade e kHz para a frequência $\omega$ , as impedâncias do condensador, o indutor e a resistência são:

Z_{C}=\dfrac{1}{\mathrm{i}\,10\omega}\qquad Z_{L}=\dfrac{\mathrm{i}\,\omega}{1% 0}\qquad Z_{R}=1

A impedância equivalente é,

Z=\dfrac{Z_{C}Z_{L}}{Z_{C}+Z_{L}}+Z_{R}=1-\dfrac{\mathrm{i}\,\omega}{10\omega^% {2}-10}

O fasor da tensão de saída, na resistência, é:

\mathbf{V}_{\text{out}}=\dfrac{\mathbf{V}_{\text{in}}}{Z}=\dfrac{\left(10% \omega^{2}-10\right)\mathbf{V}_{\text{in}}}{10\omega^{2}-10-\mathrm{i}\,\omega}

A função de resposta em frequência é,

\mathcal{R}=\dfrac{10\omega^{2}-10}{10\omega^{2}-10-\mathrm{i}\,\omega}

(b) O valor da função de resposta em frequência, para $\omega=1$ kHz, é igual a:

\mathcal{R}(1)=\dfrac{10-10}{10-10-\mathrm{i}\,}=0

(c) O módulo da função de resposta, $|\mathcal{R}|$ , é igual à raiz quadrada de $\mathcal{R}$ vezes o seu complexo conjugado:

|\mathcal{R}|=\left(\dfrac{10\omega^{2}-10}{10\omega^{2}-10-\mathrm{i}\,\omega% }\right)\left(\dfrac{10\omega^{2}-10}{10\omega^{2}-10+\mathrm{i}\,\omega}% \right)=\dfrac{\left|10\omega^{2}-10\right|}{\sqrt{100\omega^{4}-199\omega^{2}% +100}}

O gráfico dessa função, entre 0 e 2 kHz, é o seguinte:

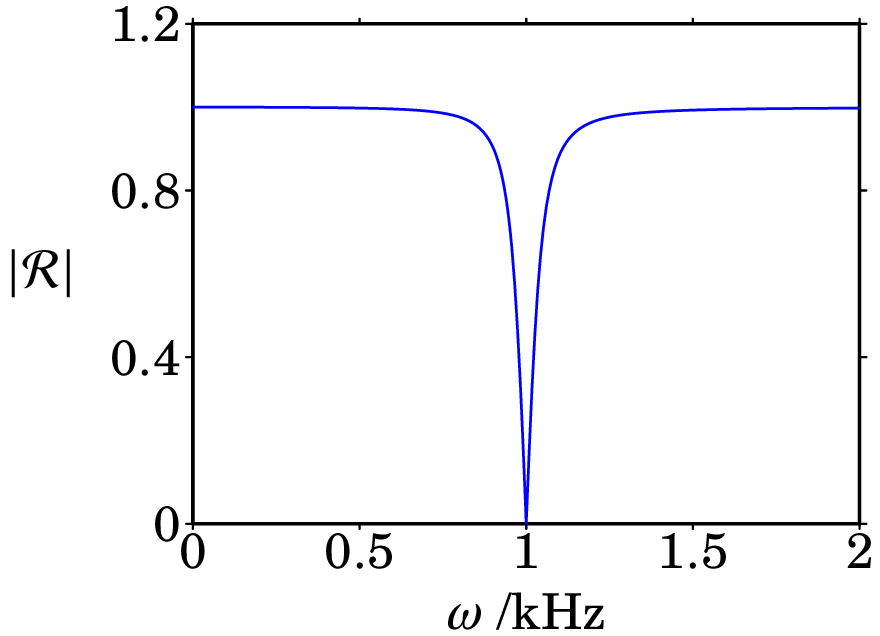
Comentários: Observe-se que, em quase todo o intervalo de frequências, $|\mathcal{R}|$ é aproximadamente igual a 1, o que implica que o sinal de entrada não é atenuado. No entanto, em $\omega=1$ kHz, $|\mathcal{R}(1)|=0$ , ou seja, o sinal de saída é nulo. É por essa razão que o filtro chama-se rejeita-banda; as frequências angulares próximas de uma frequência típica do filtro, neste caso 1 kHz, são eliminadas no sinal de saída.

Problema 10.4

A figura mostra o ecrã de um osciloscópio onde aparecem a tensão e a corrente num elemento de um circuito. As distâncias $\ell$ e $d$ foram medidas diretamente no ecrã, obtendo-se os valores $\ell=6$ cm e $d=1$ cm. O osciloscópio também permite determinar que a tensão máxima é $V_{\text{m\'{a}x}}=36$ V e a corrente máxima é $I_{\text{m\'{a}x}}=12$ mA. Com esses dados, calcule a parte real e a parte imaginária da impedância do elemento do circuito.

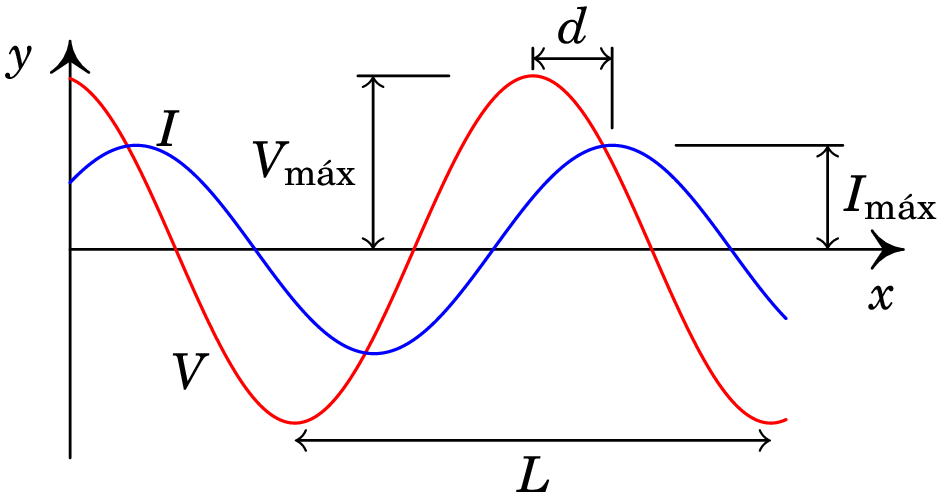
Resolução. O ângulo da impedância é igual à constante de fase da tensão menos a constante de fase da corrente:

\varphi_{Z}=\varphi_{V}-\varphi_{I}

O gráfico mostra que a tensão está adiantada em relação à corrente ( $V$ passa pelo seu valor máximo ou mínimo um pouco antes que $I$ ); a diferença das fases, $\varphi_{V}-\varphi_{I}$ , é então positiva e corresponde à distância $d$ no gráfico. Como a distância $\ell$ corresponde a um ângulo de $2\,\pi$ , então a o ângulo da impedância é:

\varphi_{Z}=\varphi_{V}-\varphi_{I}=\dfrac{d}{\ell}\,2\,\pi=\dfrac{\pi}{3}

O módulo da impedância é, em k $\Omega$ , é igual à tensão máxima em volts dividida pela corrente máxima em miliampere.

|Z|=\dfrac{V_{\text{m\'{a}x}}}{I_{\text{m\'{a}x}}}=\dfrac{36}{12}=3

A impedância, em k $\Omega$ , é o número complexo:

Z=3\,\angle\,\dfrac{\pi}{3}

E as partes real e imaginária da impedância são:

Z=3\cos\left(\dfrac{\pi}{3}\right)+\mathrm{i}\,3\sin\left(\dfrac{\pi}{3}\right% )=(1.5+\mathrm{i}\,2.598)\;\mathrm{k}\Omega

Problema 10.5

No filtro de frequências representado no diagrama, o sinal de entrada é a tensão $V_{\text{in}}$ de uma fonte de tensão alternada, com frequência angular $\omega$ , e o sinal de saída é a tensão $V_{\text{out}}$ medida no indutor e no condensador, como indica a figura. Encontre a expressão da função de resposta em frequência.

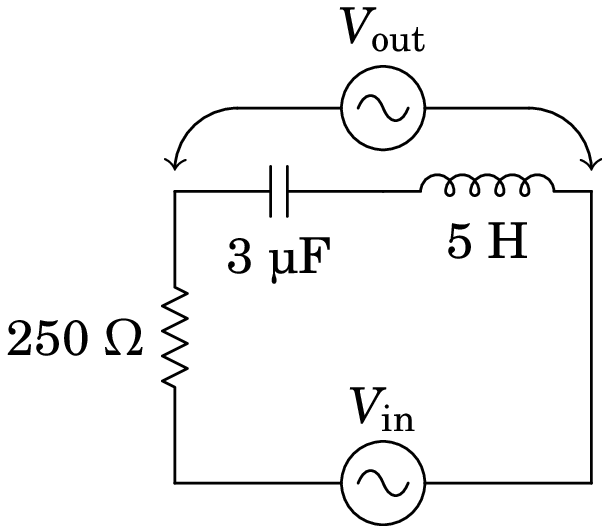
Resolução. Como 1 $\Omega$ = 1/(F·Hz), então 1 k $\Omega$ = 1/(µF·kHz) e pode usar-se unidades de k $\Omega$ para a resistência, µF para a capacidade e kHz para as frequências $s$ e $\omega$ . 1 H = 1 $\Omega$ /Hz = 1 k $\Omega$ /kHz e então a indutância deve ser dada em H. A resistência, o condensador e o indutor estão em série e a impedância dessa combinação em série é:

Z_{\mathrm{s}}=0.25-\dfrac{\mathrm{i}}{3\omega}+\mathrm{i}\,5\omega=\dfrac{% \mathrm{i}\,15\omega^{2}+0.75\omega-\mathrm{i}}{3\omega}

E o fasor da tensão de saída determina-se usando a lei de divisão de voltagem:

\mathbf{V}_{\text{out}}=\dfrac{-\mathrm{i}/(3\omega)+\mathrm{i}\,5\omega}{Z_{% \mathrm{s}}}=\dfrac{-\mathrm{i}+\mathrm{i}\,15\omega^{2}}{\mathrm{i}\,15\omega% ^{2}+0.75\omega-\mathrm{i}}\mathbf{V}_{e}

A função de resposta em frequência é:

\mathcal{R}=\dfrac{1-15\omega^{2}}{1-15\omega^{2}+\mathrm{i}\,0.75\omega}

Problema 10.6

No circuito representado no diagrama, determine a potência média fornecida pela fonte, sabendo que esta tem frequência de 30 Hz e voltagem máxima de 9 V.

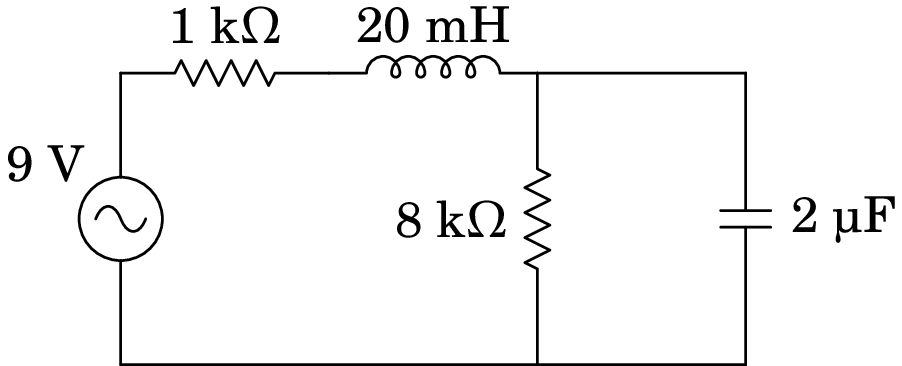
Resolução. Usando unidades de k $\Omega$ para a impedância e µF para a capacidade, o tempo deverá ser medido então em ms, a frequência em kHz e a indutância em H. Como tal, a frequência angular em kHz é:

\omega=2\pi f=0.06\pi=0.188496

As impedâncias do indutor e do condensador, em k $\Omega$ , são:

Z_{L}=\mathrm{i}\,0.02\omega=\mathrm{i}\,0.00377\qquad Z_{C}=-\dfrac{\mathrm{i% }}{2\omega}=-\mathrm{i}\,2.65258

A impedância do condensador em paralelo com a resistência de 8 k $\Omega$ é,

Z_{\text{p}}=\dfrac{8Z_{C}}{8+Z_{C}}=-\dfrac{\mathrm{i}\,21.22066}{8-\mathrm{i% }\,2.65258}=0.79241-\mathrm{i}\,2.38984

A impedância total entre os terminais da fonte é então:

Z=1+Z_{L}+Z_{\text{p}}=1.7924-\mathrm{i}\,2.3861=2.984\,\angle-0.9265

E a potência média fornecida pela fonte é

\bar{P}=\dfrac{1}{2}\,V_{\mathrm{max}}I_{\mathrm{max}}\cos\varphi_{Z}=\dfrac{V% _{\mathrm{max}}^{2}\cos\varphi_{Z}}{2|Z|}=\dfrac{81\cos(-0.9265)}{2\times 2.98% 4}=8.15

Como a voltagem foi dada em volts e a impedância em k $\Omega$ , as unidades desta potência calculada são mW.

Problema 10.7

No filtro de frequências representado no diagrama, o sinal de entrada é a tensão $V_{\mathrm{e}}$ de uma fonte de tensão alternada, com frequência angular $\omega$ , e o sinal de saída é a tensão $V$ medida no condensador, como indica a figura. Encontre a expressão da função de resposta em frequência, em função de $\omega$ .

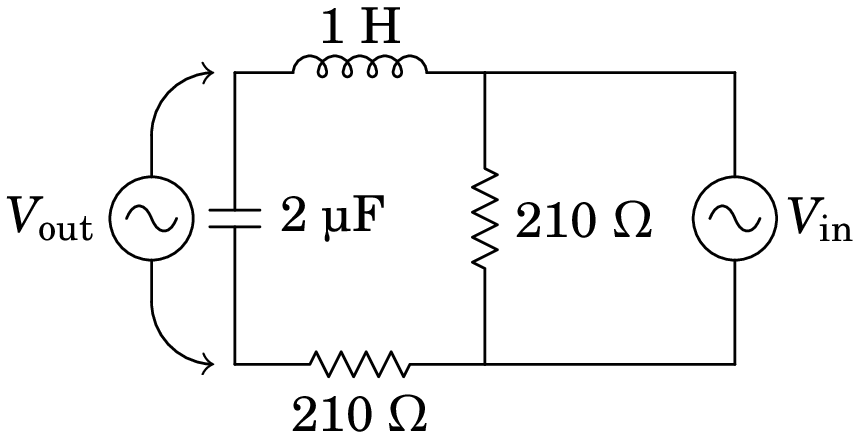
Resolução. Usando unidades de µC para a capacidade e H para a indutância, como $LC=-Z_{L}/(Z_{C}\omega^{2})$ tem unidades de tempo ao quadrado, então o tempo deverá ser medido em ms e a frequência em kHz. As impedâncias deverão então ser medidas em k $\Omega$ . Nessas unidades, os valores das impedâncias das resistências, do indutor e do condensador no circuito, em função de $\omega$ , são:

Z_{R}=0.21\qquad Z_{L}=\mathrm{i}\,\omega\qquad Z_{C}=-\dfrac{\mathrm{i}}{2\omega}

No ramo onde está o condensador,a série do condensador, o indutor e uma a resistência de 210 $\Omega$ tem impedância total:

Z_{\mathrm{s}}=0.21+\mathrm{i}\,\omega-\dfrac{\mathrm{i}}{2\omega}=\dfrac{0.42% \omega+\mathrm{i}\,2\omega^{2}-\mathrm{i}}{2\omega}

O fasor da tensão nesse ramo é o mesmo fasor da tensão de entrada, $\mathbf{V}_{\mathrm{in}}$ . Como tal, o fasor da tensão no condensador é igual a:

\mathbf{V}_{\text{out}}=\dfrac{Z_{C}}{Z_{\mathrm{s}}}\mathbf{V}_{\mathrm{in}}=% -\frac{\mathrm{i}}{0.42\omega+\mathrm{i}\,2\omega^{2}-\mathrm{i}}\mathbf{V}_{% \mathrm{in}}

A função de resposta em frequência é:

\mathcal{R}=\dfrac{1}{1-2\omega^{2}+\mathrm{i}\,0.42\omega}

em que a frequência angular $\omega$ é dada em kHz.

Problema 10.8

A fonte no circuito representado no diagrama tem voltagem máxima 9 V e frequência angular $\omega=125$ kHz. Determine a voltagem máxima no condensador de 2 nF.

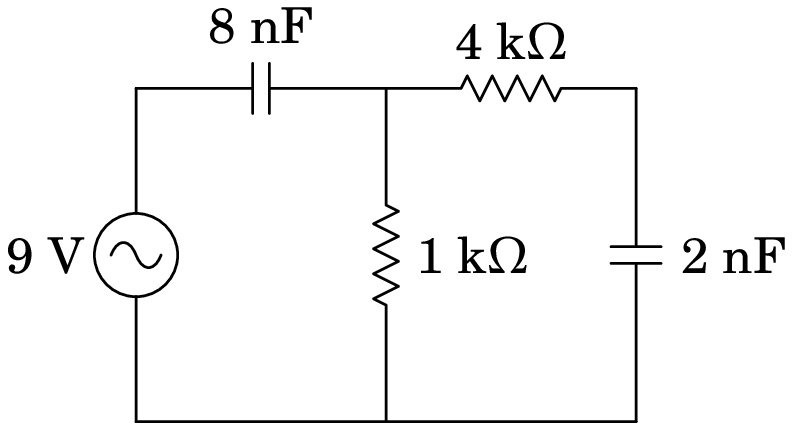
Resolução. As impedâncias complexas dos dois condensadores são, em $\Omega$ ,

	$\displaystyle Z_{1}=\dfrac{-\mathrm{i}}{125\times 10^{3}\times 8\times 10^{-9}% }=-\mathrm{i}\,1000$
	$\displaystyle Z_{2}=\dfrac{-\mathrm{i}}{125\times 10^{3}\times 2\times 10^{-9}% }=-\mathrm{i}\,4000$

Como tal, com as impedâncias em k $\Omega$ e as voltagens em V, o circuito é o seguinte:

Para determinar o fasor $\mathbf{V}$ , usam-se circuitos equivalentes mais simples, da forma seguinte:

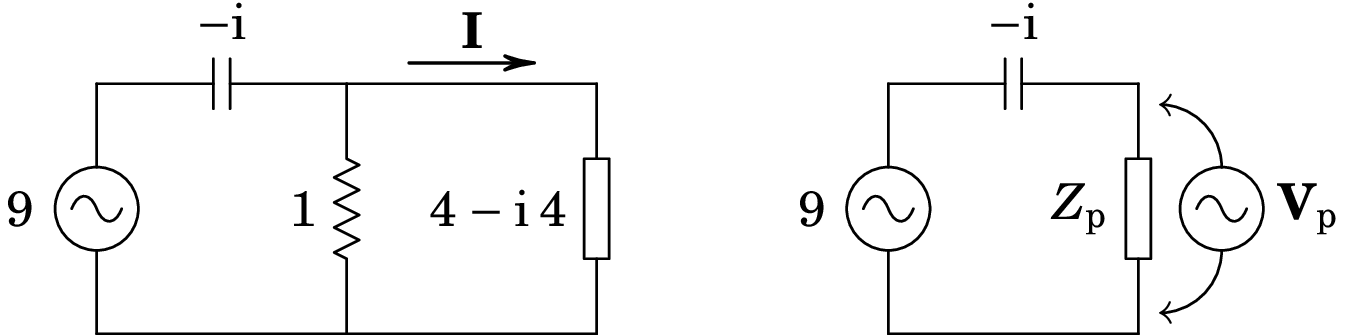
Onde a impedância em paralelo e a impedância total são:

Z_{\mathrm{p}}=\dfrac{4-\mathrm{i}\,4}{5-\mathrm{i}\,4}\qquad\qquad Z_{\mathrm% {t}}=-\mathrm{i}+\dfrac{4-\mathrm{i}\,4}{5-\mathrm{i}\,4}=\dfrac{9}{4+\mathrm{% i}\,5}

O fasor da corrente total é (em mA),

\mathbf{I}_{\mathrm{t}}=\dfrac{9}{\dfrac{9}{4+\mathrm{i}\,5}}=4+\mathrm{i}\,5

O fasor da voltagem na impedância $Z_{\mathrm{p}}$ é:

\mathbf{V}_{\mathrm{p}}=\left(\dfrac{4-\mathrm{i}\,4}{5-\mathrm{i}\,4}\right)% \left(4+\mathrm{i}\,5\right)=4+\mathrm{i}\,4

E os fasores da corrente e da voltagem no condensador de 2 nF são:

\mathbf{I}=\dfrac{4+\mathrm{i}\,4}{4-\mathrm{i}\,4}=\mathrm{i}\qquad\qquad% \mathbf{V}=-\mathrm{i}\,4\times\mathrm{i}=4

Ou seja, a voltagem máxima nesse condensador é igual a 4 V.