6. Circuitos de corrente contínua
Problema 6.1
Determine a resistência equivalente entre os pontos A e B.
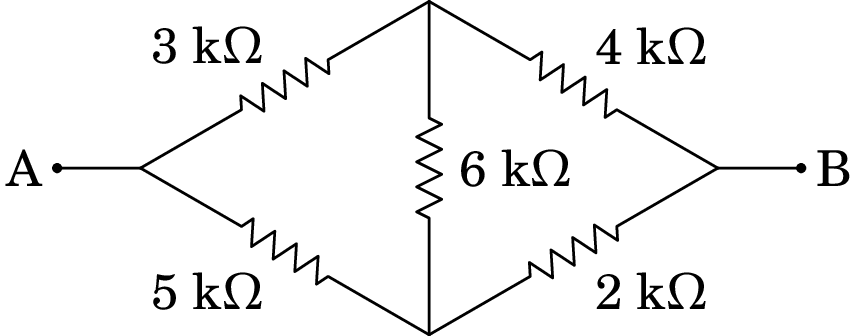
Resolução. Usando a transformação delta-estrela, o triângulo formado pelas resistências de 4 k, 2 k e 6 k pode ser substituído pelas 3 resistências:
e o circuito inicial fica equivalente ao seguinte circuito:

As resistências de 3 k e 2 k estão em série e as resistências de 5 k e 1 k também. Combinando estas resistências, o novo circuito equivalente é o seguinte:
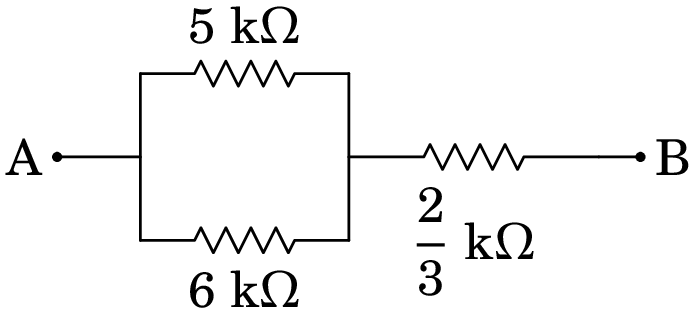
As resistências de 5 k e 6 k, em paralelo, podem ser substituídas pela resistência equivalente,
E o circuito fica com apenas duas resistências em série entre A e B:
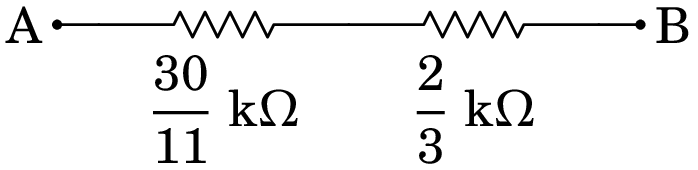
A resistência total entre A e B é 112/33 k, aproximadamente igual a 3.394 k.
Problema 6.2
Considere duas resistências e ligadas em paralelo. Uma corrente total distribui-se entre as duas resistências, passando corrente por e corrente por . Admita que as correntes e podem tomar qualquer valor (inclusivamente negativo) desde que . Determine os valores de e que minimizam a potência dissipada por efeito Joule nas resistências, e mostre que se obtém o resultado da equação (6.19) do livro.
Resolução. Considerando as correntes e variáveis, mas fixa, a potência dissipada em cada uma das resistências pode ser escrita em função de apenas uma das variáveis; por exemplo, em função de :
A potência total dissipada, igual à soma das potências dissipadas nas duas resistências, é:
O valor da variável que faz com que a potência tenha um ou mais extremos é o valor de para o qual a derivada de em ordem a é nula:
Este valor de corresponde, de facto, a um mínimo da potência pois a segunda derivada é positiva:
Substituindo em , obtém-se então:
As expressões obtidas para as duas correntes coincidem com a equação (6.19) e mostram que a corrente elétrica se divide pelas duas resistências em paralelo de modo a minimizar a potência dissipada, i.e., a minimizar a energia dissipada por efeito de Joule.
Problema 6.3
No circuito da figura, determine quais das fontes de força eletromotriz fornecem ou absorvem energia e calcule a potência fornecida, ou absorvida, por cada uma.
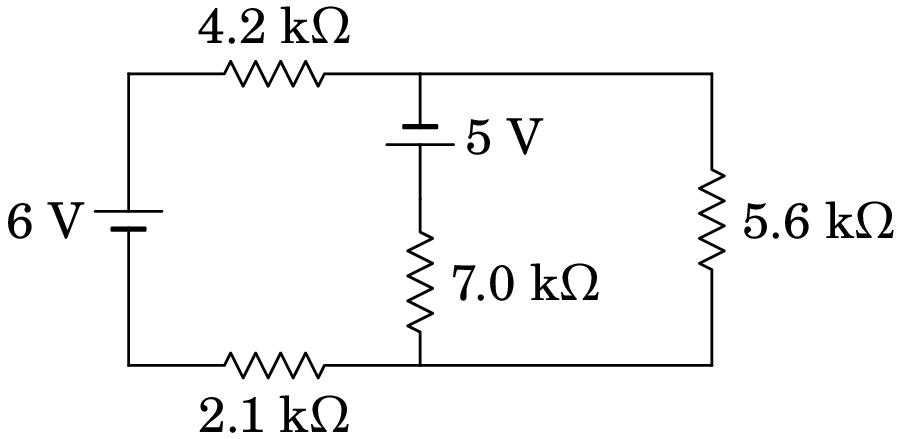
Resolução. O circuito têm dois nós, A e B, tal como mostra a figura seguinte, e três ramos entre esses nós. Em cada ramo podemos trocar a ordem das resistências e das fontes ficando o circuito da forma seguinte:

No diagrama acima, as f.e.m. das fontes estão em volt e as resistências em k. Como tal, as correntes que vamos calcular terão unidades de mA. Se arbitrarmos que o potencial no nó A é 0, então,
Podemos agora escrever as correntes nos três ramos em função do potencial do nó B, arbitrando que todas vão do nó B para o nó A:
A lei dos nós em B implica que a soma dessas três correntes tem de ser igual a zero:
Multiplicando por fica,
e resolvendo para obtém-se:
Substituindo esse potencial nas expressões das três correntes acima temos:
O resultado positivo para indica que a corrente de facto circula de D para A, e então a fonte de 5 V está a fornecer potência, com valor:
No caso da fonte de 6 V, o sinal negativo de indica que a corrente circula de A para C. Como tal, a fonte de 6 V também fornece potência igual a:
Problema 6.4
Uma resistência de 2.7 k liga-se a duas pilhas, em
paralelo, ambas com a mesma f.e.m. de 9 V, mas com diferentes
resistências internas, tal como mostra o digrama seguinte.
(a) Determine a corrente na resistência de 2.7 k.
(b) Qual das duas pilhas fornece maior potência?
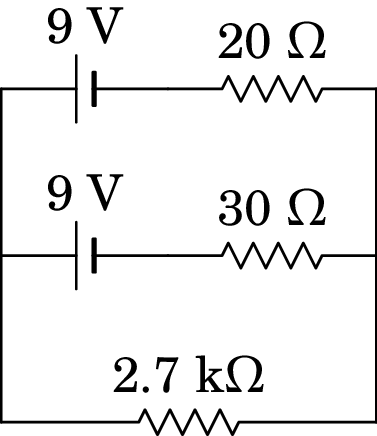
Resolução. (a) O circuito tem dois nós, A e B, e três ramos entre eles; usando unidades SI para as voltagens e resistências o diagrama do circuito é o seguinte:

Podemos arbitrar que o potencial no ponto A é igual a 9 V e, portanto, o potencial nos pontos C e D será nulo. No ramo da resistência de 2.7 k, não há dúvida que a corrente circulará de A para B. Assim, o potencial no ponto B será menor que 9 V e a corrente nessa resistência é:
Nas duas fontes de resistências internas 20 e 30 , as correntes são ambas de B para A e com intensidades:
A lei dos nós em B é,
Multiplicando por 2700:
e substituindo na expressão da corrente na resistência de 2.7 k,
(b) Olhando para as expressões das correntes e na alínea anterior, conclui-se que . E, como as f.e.m. das duas pilhas são iguais, então a pilha com maior corrente é a que mais potência fornece, ou seja, a pilha com resistência interna menor (20 ) é a que fornece maior potência.
Problema 6.5
Uma fonte com voltagem é ligada a uma
resistência , mas pretende-se que a voltagem nessa resistência
seja reduzida para , menor do que a voltagem de
entrada . Para conseguir esse objetivo, usa-se
um circuito chamado atenuador. A figura mostra, dentro da
caixa a tracejado, um possível circuito atenuador que tem a vantagem
de permitir fazer com que a resistência entre os pontos de entrada A
e B continue igual à resistência do dispositivo ligado entre os
pontos de saída C e D.
(a) Mostre que para que a
resistência entre A e B seja igual a , as resistências e
do atenuador devem verificar a condição:
(b) Se e verificam a condição da alínea anterior, mostre que o fator de atenuação, é dado pela expressão:
(c) Determine os valores de e que fazem com que a resistência entre A e B seja igual a , com atenuação .
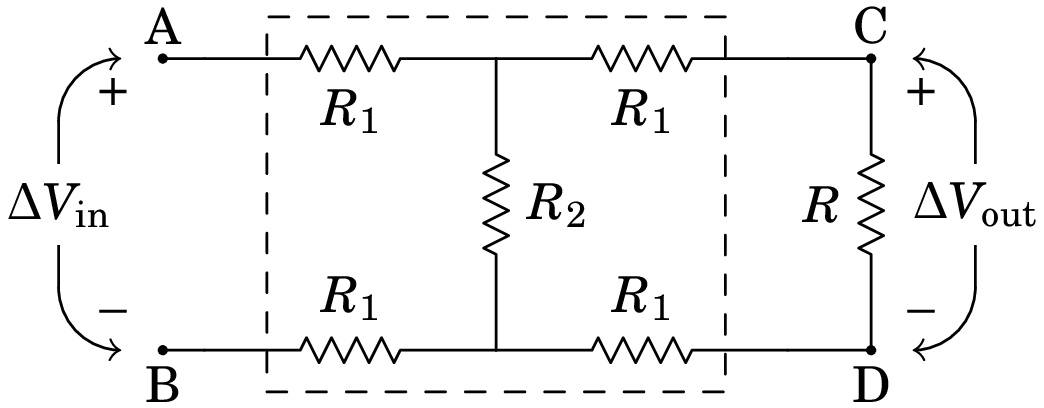
(Problema retirado de Nilsson e Riedel 2015, pág. 117)
Resolução. (a) A resistência soma-se às duas resistências próximas dela, que estão em série com ela, e o resultado combina-se em paralelo com a resistência , dando a resistência equivalente:
O circuito é então equivalente ao seguinte circuito mais simples:
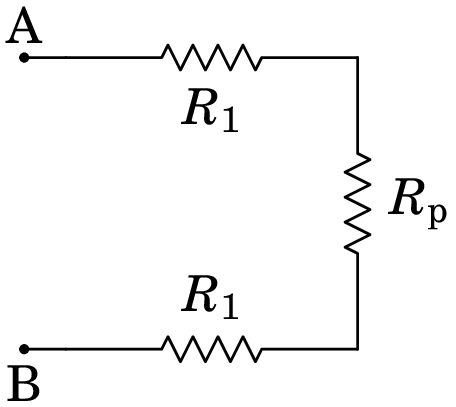
e a resistência entre A e B é igual a:
igualando essa expressão a obtém-se:
(b) No circuito da figura acima, com duas resistências em série com , sendo e , o princípio da divisão de voltagem permite determinar a diferença de potencial em :
diferença de potencial essa que é a mesma do que no ramo com duas resistências em série com , no circuito inicial. Usando novamente o princípio da divisão de voltagem obtém-se:
e o fator de atenuação é:
(c) Substituindo os valores dados nas expressões obtidas nas duas alíneas anteriores, obtém-se o seguinte sistema não-linear:
A segunda equação permite determinar em função de :
e substituindo na primeira equação obtém-se uma equação quadrática para :
A raiz positiva é , que conduz ao valor de (a raiz negativa não interessa).
Problema 6.6
Determine a potência dissipada em cada resistência no circuito representado no diagrama e a potência fornecida pela f.e.m. Verifique que a potência fornecida pela f.e.m. é igual à soma das potências dissipadas em todas as resistências.
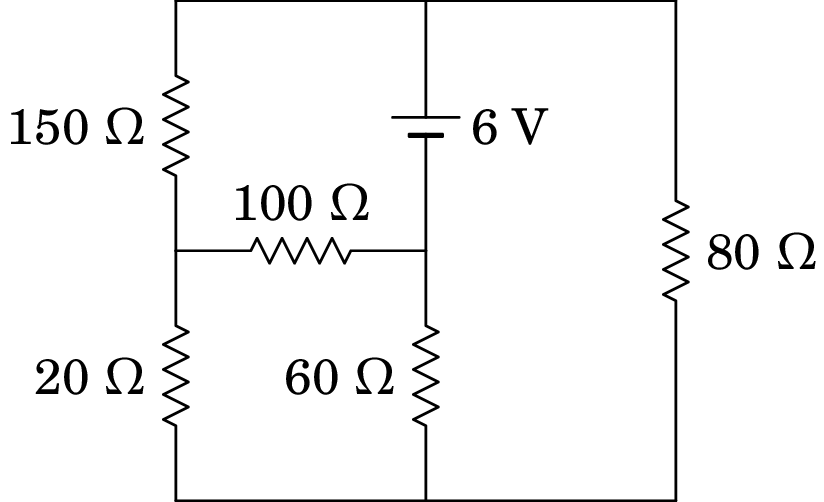
Resolução. Para determinar a potência dissipada em cada resistência, basta encontrar os potenciais dos 4 nós do circuito e em cada resistência dividir a diferença de potencial, ao quadrado, pelo valor da resistência.
As resistências de 20 , 100 e 60 , em configuração delta, podem ser substituídas por três resistências em estrela, com os seguintes valores:
Com essa substituição, o circuito equivalente é o seguinte, em que os 4 nós do circuito original são A, B, C e D (unidades SI):

Combinam-se as resistências de 150 e 100/9, em série, e as resistências de 80 e 20/3, em série, ficando o circuito do lado esquerdo da seguinte figura. A seguir combinam-se as resistências de 1450/9 e 260/3, em paralelo, ficando o circuito do lado direito da figura seguinte:
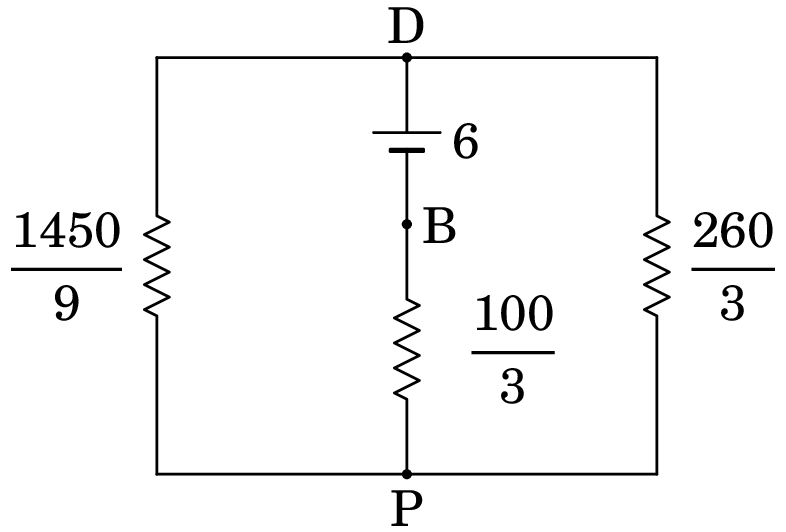
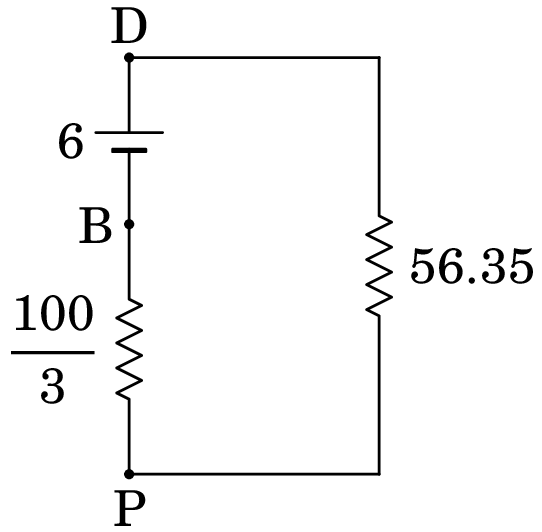
Os 6 V da f.e.m. dividem"se entre as duas resistências da forma seguinte (a corrente é no sentido anti-horário):
No diagrama acima, com os pontos A e C, os V entre D e P dividem-se da forma seguinte:
As voltagens nas resistências em delta entre A, B e C são:
Resumindo, as voltagens e potências dissipadas nas resistências são:
| Resistência / | Voltagem /V | Potência / mW |
| 20 | 0.045 | |
| 60 | 105.84 | |
| 80 | 151.38 | |
| 100 | 62.001 | |
| 150 | 82.134 |
A potência total dissipada no circuito, igual à soma das potências dissipadas nas resistências, é igual a 401.4 mW. A corrente que passa pela f.e.m. é a mesma do que na resistência de 100/3 , que é igual a:
e a potência fornecida pela f.e.m. é igual a mW, que é exatamente igual à potência total dissipada no circuito.
Problema 6.7
No circuito representado no diagrama, os dois condensadores
estão inicialmente descarregados. Determine:
(a) As correntes iniciais nas resistências e condensadores.
(b) As cargas finais nos condensadores, indicando as suas
polaridades.
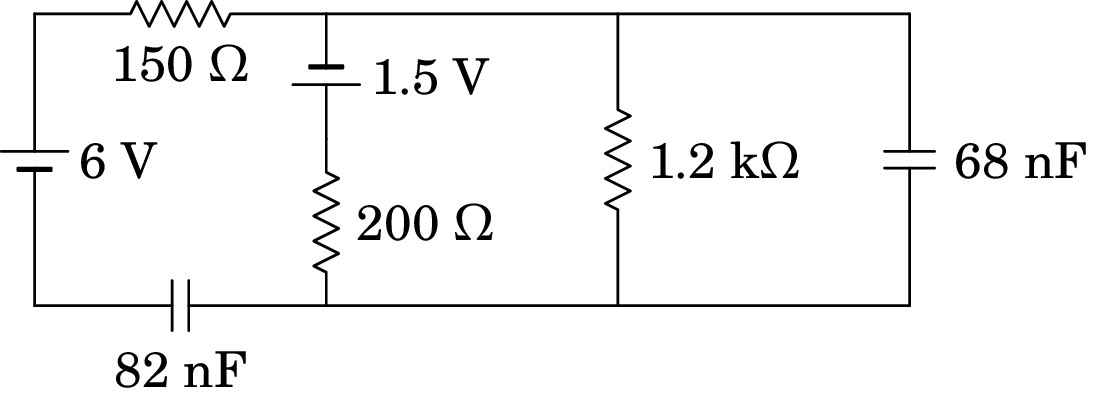
Resolução. (a) No instante inicial, em que os condensadores descarregados atuam como curto-circuitos, o circuito equivalente é o seguinte
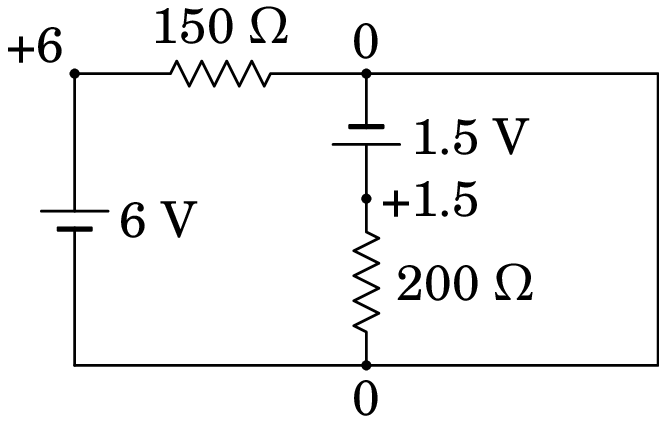
A resistência de 1.2 k não foi representada, porque o equivalente dessa resistência em paralelo com o condensador de 68 nF (curto-circuito com resistência nula) é uma resistência nula (curto-circuito).
Arbitrando potencial nulo no ponto onde o elétrodo negativo da f.e.m. de 1.5 V está em contacto com a resistência de 150 , o elétrodo negativo da f.e.m. de 6 V também terá potencial nulo, porque o potencial em todos os pontos no curto-circuito à direita do circuito é o mesmo. Como tal, o potencial no elétrodo positivo da f.e.m. de 1.5 V será 1.5 V, e o potencial do elétrodo positivo da f.e.m. de 6 V será 6 V, tal como mostra o diagrama acima.
Na resistência de 150 a diferença de potencial é 6 V e a corrente será 6/150 = 0.04 A (de esquerda para direita), que é a mesma corrente no condensador de 82 nF (de direita para esquerda). Na resistência de 200 , a diferença de potencial é 1.5 V e a corrente 1.5/200 = 0.0075 A (de cima para baixo). Pela regra dos nós, a corrente no condensador de 68 nF é então, A (de cima para baixo). Na resistência de 1.2 k a corrente é nula, porque a diferença de potencial é nula.
(b) No estado final, quando os condensadores completamente carregados são equivalentes a interruptores abertos, o circuito equivalente é o seguinte
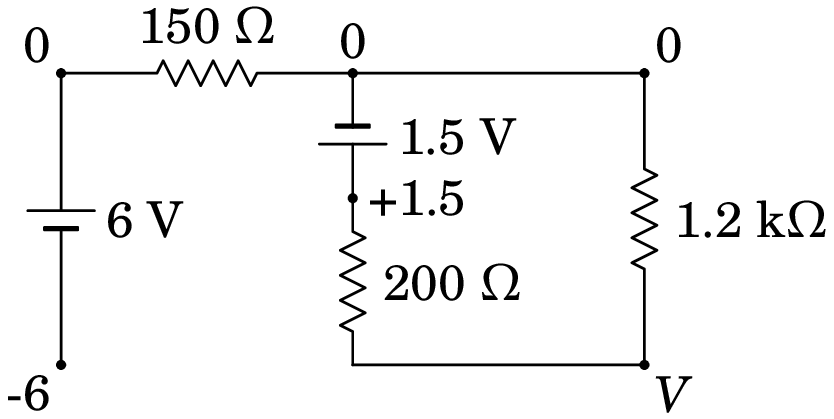
Observe-se que a corrente na resistência de 150 é nula, porque não tem percurso por onde circular. Como tal, o potencial nos dois extremos dessa resistência é o mesmo e pode arbitrar-se que é nulo, como mostra o diagrama anterior. O potencial no elétrodo negativo da f.e.m. de 6 V será então igual a V e o potencial no elétrodo positivo da f.e.m. de 1.5 V será igual a 1.5 V.
No ponto comum às resistências de 200 e 1.2 k o valor do potencial, no diagrama, pode ser obtido por divisão de voltagem (1.5 V dividido entre as resistências de 200 e 1.2 k ):
Observa-se então que no condensador de 82 nF a carga é positiva na armadura do lado direito (maior potencial), no condensador de 68 nF a carga é negativa na armadura de cima (menor potencial) e os valores das cargas nesses dois condensadores são os seguintes:
Problema 6.8
Relativamente ao circuito da figura abaixo:
(a) Determine a intensidade e sentido da corrente
no instante inicial no condensador, sabendo que este estava
inicialmente descarregado.
(b) Determine a carga final no condensador, indicando a sua
polaridade.
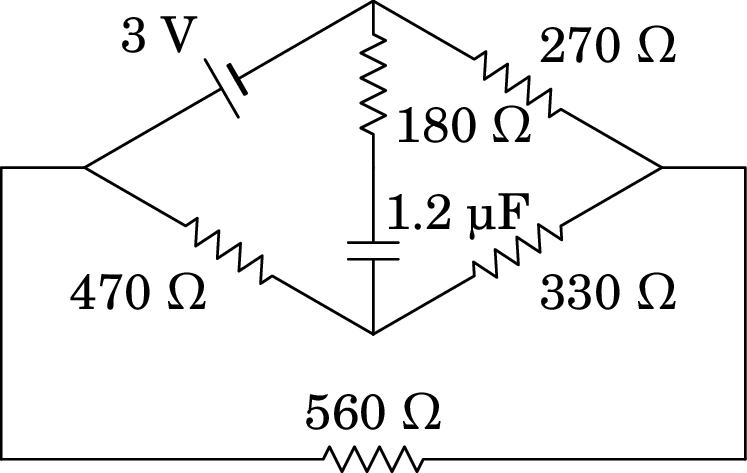
Resolução. (a) No estado inicial, com o condensador em curto-circuito, as resistências de 180 , 270 e 330 formam um delta, que pode ser substituído pelas seguintes três resistências em estrela:
E o circuito equivalente, com todas as resistências em unidades de , é o seguinte:
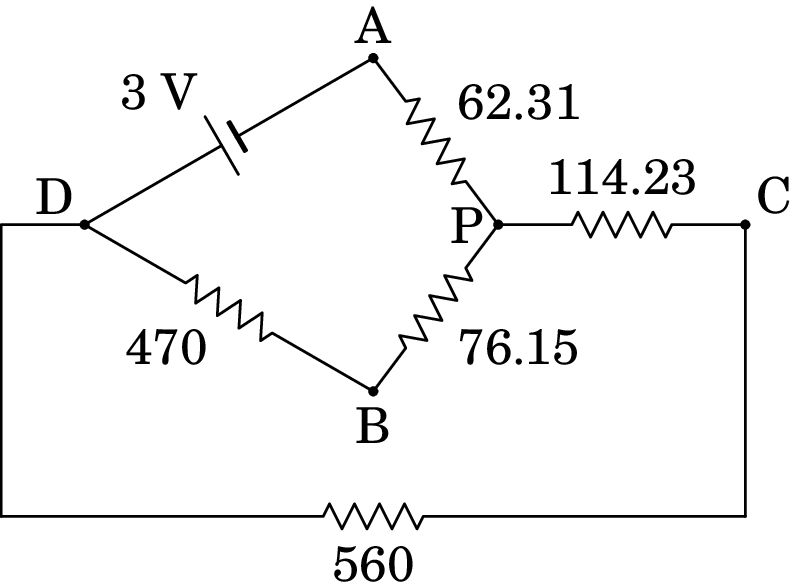
As resistências de 470 e 76.15, em série, substituem-se por uma resistência de 546.15 e as resistências de 114.23 e 560, também em série, substituem-se por uma resistência de 674.23. A seguir, as resistências de 546.15 e 674.23, em paralelo, substituem-se por uma resistência de . Os dois circuitos resultantes dessas duas simplificações são os seguintes:
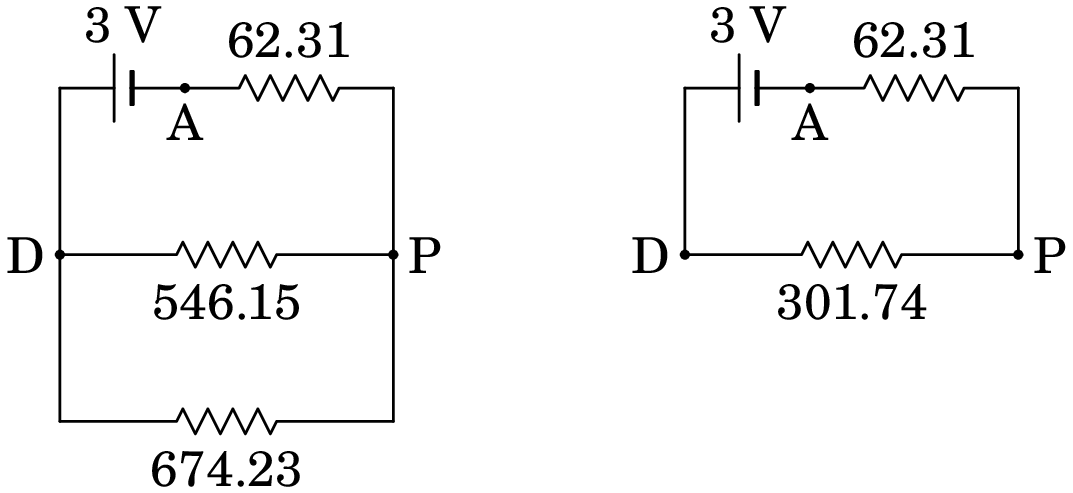
No circuito do lado direito, as diferenças de potencial entre os pontos A, P e D são as seguintes:
e, como entre os pontos D e P estavam as resistências de 470 e 76.15, em série, com o ponto B entre elas, então:
A diferença de potencial entre A e B é igual a:
E, com o condensador em curto-circuito, a resistência entre A e B é de 180 e a corrente nesse ramo é igual a:
Ou seja, no instante inicial a corrente no condensador é 4.78 mA, de B para A (de baixo para cima).
(b) O circuito equivalente no estado final, com o condensador como interruptor aberto, é o seguinte
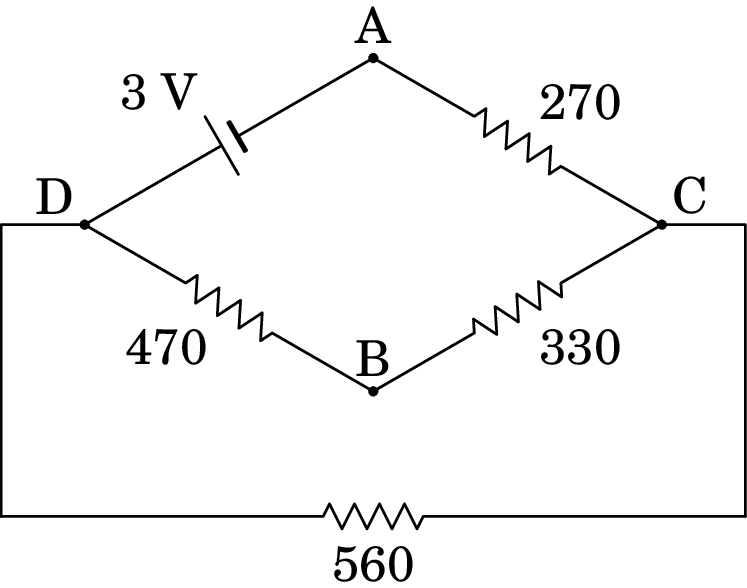
Onde as resistências de 470 e 330 estão em série entre C e D, e a resistência equivalente ficará em paralelo com a resistência de 560, conduzindo aos seguintes circuitos equivalentes mais simples:

No circuito do lado direito, as diferenças de potencial entre os pontos A, C e D são as seguintes:
e, como entre os pontos D e C estavam as resistências de 470 e 330, em série, com o ponto B entre elas, então:
A diferença de potencial entre A e B é igual a:
O resultado positivo indica que a carga é positiva na armadura de baixo (maior potencial em B do que em A) e negativa na armadura de cima. Finalmente, a carga no condensador calcula-se a partir da sua voltagem