4. Energia eletrostática e capacidade

Problema 4.1

Em cada caso determine a velocidade final da partícula após ser acelerada no vácuo, desde o repouso, usando a diferença de potencial dada:
(a) Um eletrão, com uma diferença de potencial de 220 V.
(b) Um eletrão num dispositivo de raios X em que é usada uma diferença de potencial de 5 kV.
(c) Um protão, no acelerador LHC (Large Hadron Collider) do CERN, em que é usada uma diferença de potencial de $7\times {10}^{12}$ V.

Resolução. (a) A energia eletrostática transferida para o eletrão é 220 eV, que será convertida em energia cinética $E_{\mathrm{c}}$. Para um eletrão, $m{c}^2=0.5111$ MeV; o fator gama do eletrão é:

$$\gamma =1+\frac{220}{0.5111\times {10}^6}=1.0004$$

Como tal, podemos usar a expressão não-relativista da energia cinética para determinar a velocidade:

$$v=\sqrt{\frac{2E_{\mathrm{c}}}{m}}=\sqrt{\frac{2\times 220\times 1.602\times {10}^{-19}}{9.109\times {10}^{-31}}}=8.80\times {10}^6\mathrm{m}/\mathrm{s}$$

(b) A energia cinética ganha pelo eletrão é agora 5 keV e o factor gama é,

$$\gamma =1+\frac{5\times {10}^3}{0.5111\times {10}^6}=1.00978$$

que já mostra efeito relativista. A velocidade calcula-se a partir do factor gamma

$$v=c\sqrt{1-\frac{1}{{\gamma }^2}}=4.16\times {10}^7\mathrm{m}/\mathrm{s}$$

(No cálculo de $v$ a partir de $\gamma$, esta última tem de ser dada com bastante precisão para evitar erro numérico).

(c) A energia do protão é $7\times {10}^{12}$ eV (7 tera eletrão-volt). Como um protão têm $m{c}^2=0.9366$ GeV, o fator gama deste protão é:

$$\gamma =1+\frac{7\times {10}^{12}}{0.9366\times {10}^9}=7475$$

que corresponde a uma partícula altamente relativista, com velocidade praticamente igual à velocidade da luz. A velocidade, em relação à velocidade da luz é:

$$v=c\sqrt{1-\frac{1}{{\gamma }^2}}=0.999999991c$$

Problema 4.2

Uma partícula pontual com massa de 1.5 µg e carga de 12 nC encontra-se numa região onde existe vácuo e um campo elétrico constante de módulo 2.3 kV/m com direção e sentido do eixo $x$. Se num instante inicial a partícula estiver em repouso em $x=-3$ cm, determine com que velocidade esta passará pela posição $x=3$ cm.

Resolução: Por ser uma partícula macroscópica, seria necessário um campo muito mais elevado para produzir efeito relativista e usaremos mecânica não-relativista. A diferença de potencial entre as posições $x=-3$ cm e $x=3$ cm, em unidades SI, é:

$$\mathrm{\Delta }V=V(0.03)-V(-0.03)=-{\int }_{-0.03}^{0.03}\overrightarrow{E}\cdot (\hat{ı}\mathrm{d}x)=-{\int }_{-0.03}^{0.03}2300dx=-138\mathrm{V}$$

a variação da energia potencial elétrica da partícula durante o percurso é:

$$\mathrm{\Delta }{E}_{\mathrm{p}}=q\mathrm{\Delta }V=-1.656\times {10}^{-6}\mathrm{J}$$

O sinal negativo indica que a partícula perde energia potencial e, como no vácuo não há forças dissipativas, a energia mecânica conserva-se e a diminuição da energia potencial será igual ao aumento da energia cinética:

$$\frac{1}{2}m{v}^2=\frac{1.5\times {10}^{-9}}{2}{v}^2=1.656\times {10}^{-6}\mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}v=47.0\mathrm{m}/\mathrm{s}$$

Comentário: Observe-se que a aceleração da partícula é constante e com módulo:

$$a=\frac{qE}{m}=18400\mathrm{m}/{\mathrm{s}}^2$$

e o tempo que demora o percurso é:

$$\mathrm{\Delta }t=\frac{\mathrm{\Delta }v}{a}=2.5\mathrm{ms}$$

A distância que a partícula cai, pelo efeito da gravidade, durante esse intervalo é desprezável comparada com os 6 cm que percorre. Como tal, não é necessário saber qual é a posição do eixo $x$ referido em relação ao plano horizontal.

Problema 4.3

(a) Determine a capacidade de uma esfera condutora isolada, com raio de 4.0 cm e rodeada por ar.
(b) A esfera da alínea anterior é coberta com uma camada de vidro de 1 mm de espessura e constante dielétrica de 5.6, deixando um orifício para ligar um cabo à esfera, e a camada de vidro é coberta com uma segunda lâmina metálica esférica de raio 4.1 cm, formando-se assim um condensador esférico. Determine a capacidade desse condensador.
(c) Qual a relação entre a capacidade do condensador e a da esfera?

Resolução. (a) Admitindo que a constante dielétrica do ar é $K=1$, a capacidade da esfera é:

$$C=\frac{KR}{k}=\frac{4\times {10}^{-2}}{8.988\times {10}^9}=4.45\times {10}^{-12}\mathrm{F}=4.45\mathrm{pF}$$

(b) A capacidade do condensador esférico é:

$$C=\frac{K{R}_1{R}_2}{k\left(R_2-R_1\right)}=\frac{5.6\times 4\times {10}^{-2}\times 4.1\times {10}^{-2}}{8.988\times {10}^9\left(4.1\times {10}^{-2}-4\times {10}^{-2}\right)}=1.02\mathrm{nF}$$

(c) A relação entre as duas capacidades é,

$$\frac{1.02\times {10}^{-9}}{4.45\times {10}^{-12}}=229$$

Comentários: O resultado da alínea c mostra a utilidade dos condensadores. A capacidade de armazenar carga do condensador é 230 maior do que uma única esfera. Com um único condutor não é possível obter capacidades elevadas; por exemplo, se a esfera condutora da alínea a fosse do tamanho da Terra (raio de 6371 km), a sua capacidade seria de $7.08\times {10}^{-4}$ F. Compare-se essa capacidade com as capacidades da ordem do kF nos ultracondensadores.

Problema 4.4

No sistema de três condensadores apresentado na figura, $C_1=1.2$ µF, $C_2=4.3$ µF e $C_3=2.5$ µF. A voltagem entre os pontos A e B é de 9.0 V. (a) Determine a carga armazenada em cada condensador. (b) Determine a energia total armazenada no sistema.

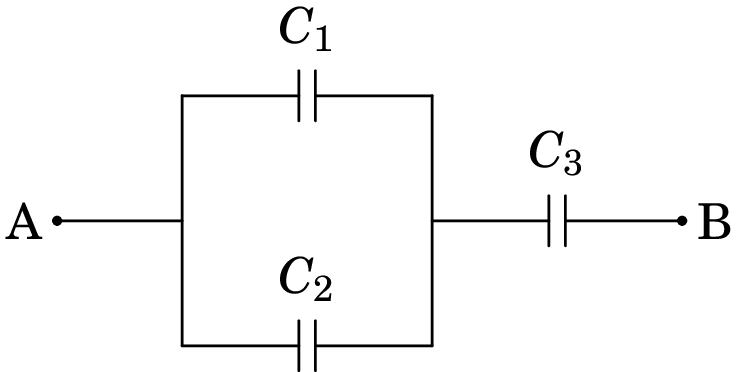
Resolução. Para resolver este tipo de problema, simplifica-se o circuito até ficar unicamente com um condensador. O primeiro passo é substituir os condensadores de capacidades $C_1$ e $C_2$, que estão em paralelo, por um condensador equivalente com capacidade $C_4$. No segundo passo, os condensadores de capacidades $C_4$ e $C_3$, que ficam ligados em série, são substituídos por um único condensador com capacidade $C_5$. A figura seguinte mostra esses passos.

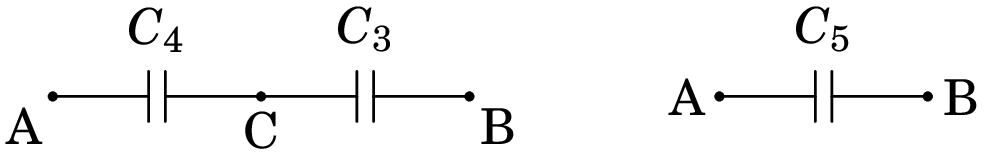
A capacidade do condensador equivalente em paralelo, entre os pontos A e C, é:

$$C_4=C_1+C_2=5.5\mu \mathrm{F}$$

E a capacidade do condensador equivalente aos condensadores com capacidades $C_4$ e $C_3$, em série, é:

$$C_5=\frac{C_4{C}_3}{C_4+C_3}=1.71875\mu \mathrm{F}$$

(a) Como a diferença de potencial entre os pontos A e B é igual 9 V, a carga armazenada no condensador de capacidade $C_5$ é:

$$Q_5=C_5\mathrm{\Delta }{V}_{\mathrm{AB}}=1.71875\times {10}^{-6}\times 9=15.5\mu \mathrm{C}$$

Que é também a carga armazenada nos condensadores de capacidades $C_3$ e $C_4$, por estarem em série

$$Q_3=Q_4=15.5\mu \mathrm{C}$$

A diferença de potencial entre os pontos A e C será:

$$\mathrm{\Delta }{V}_{\mathrm{AC}}=\frac{Q_4}{C_4}=\frac{15.47\times {10}^{-6}}{5.5\times {10}^{-6}}=2.8125\mathrm{V}$$

As cargas nos condensadores de capacidades $C_1$ e $C_2$, que estão ambos ligados entre os pontos A e C, são:

$Q_1$ $=C_1\mathrm{\Delta }{V}_{\mathrm{AC}}=1.2\times {10}^{-6}\times 2.8125=3.38\mu \mathrm{C}$

$Q_2$ $=C_2\mathrm{\Delta }{V}_{\mathrm{AC}}=4.3\times {10}^{-6}\times 2.8125=12.1\mu \mathrm{C}$

(b) A energia total armazenada no sistema é a soma das energias nos três condensadores, que será igual à energia total armazenada em qualquer um dos outros dois circuitos equivalentes na figura acima. Será então mais fácil determinar essa energia no circuito mais simples, com apenas um condensador de capacidade $C_5$ entre A e B:

$$E_p=E_5=\frac{1}{2}{C}_5\mathrm{\Delta }{V}_{\mathrm{AB}}^2=\frac{1.71875\times {10}^{-6}\times 9^2}{2}=69.6\mu \mathrm{J}$$

Problema 4.5

Uma fina barra de material dielétrico de secção reta $A$ e comprimento $L$ encontra-se no eixo $x$ entre $x=0$ e $x=L$. Existe um campo elétrico, o qual induz na barra uma polarização dada por $(a{x}^2+bx+c)\hat{ı}$, onde $a$, $b$ e $c$ são constantes. (a) Encontre a densidade volúmica da carga de polarização e a densidade superficial da carga de polarização em cada extremidade da barra. (b) Mostre que a carga total de polarização é nula, como era de esperar.

Resolução. A densidade volúmica de carga de polarização é menos a divergência do vetor de polarização:

$${\rho }_P=-\overrightarrow{\nabla }\cdot (a{x}^2+bx+c)\hat{ı}=-2ax-b$$

Na extremidade em $x=0$, o vetor de polarização é $c\hat{ı}$, o versor normal é $-\hat{ı}$ e a densidade superficial de carga de polarização é,

$${\sigma }_P=c\hat{ı}\cdot (-\hat{ı})=-c$$

Na extremidade em $x=L$, o vetor de polarização é $(a{L}^2+bL+c)\hat{ı}$, o versor normal é $\hat{ı}$ e a densidade superficial de carga de polarização é:

$${\sigma }_P=(a{L}^2+bL+c)\hat{ı}\cdot \hat{ı}=a{L}^2+bL+c$$

A carga total na extremidade em $x=0$ é

$${\sigma }_{P}A=-cA$$

A carga na extremidade em $x=L$ é

$${\sigma }_{P}A=a{L}^{2}A+bLA+cA$$

e a carga total no interior da barra é

$$A{\int }_0^L{\rho }_{P}dx=-A{\int }_0^L(2ax+b)dx=-a{L}^{2}A-bLA$$

e a soma das cargas nas extremidades mais ca carga interna é zero.

Problema 4.6

No circuito da figura, calcule a capacidade equivalente: (a) Entre os pontos B e D. (b) Entre os pontos A e B.

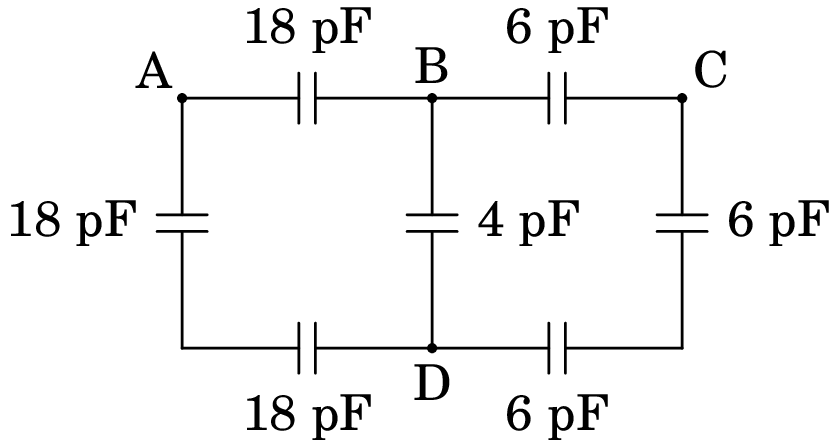
(a) Para determinar a capacidade entre B e D, imagine-se que é ligado entre esses dois pontos um medidor de capacidades, representado por F, na figura seguinte:

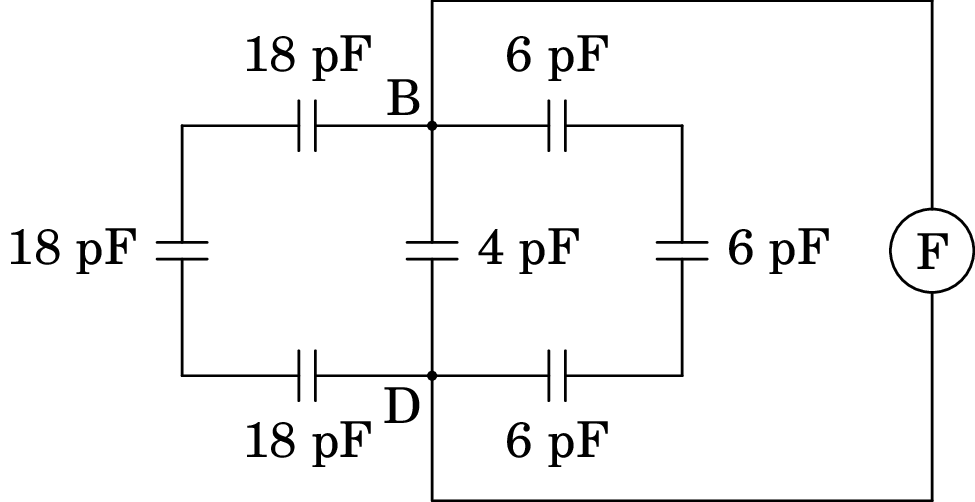
O dispositivo de medição teria de inserir cargas de sinais opostos nos pontos B e D e medir a voltagem devida a essas cargas. As cargas têm 3 percursos alternativos ao entrar nos ponto B e D. Um desses percursos é passando pelos 3 condensadores de 18 pF, que estão em série, e outro dos percursos passa pelos 3 condensadores de 6 pF, também em série. Esses condensadores em série podem ser substituídos pelos condensadores equivalentes com capacidades:

$${\left(\frac{1}{18}+\frac{1}{18}+\frac{1}{18}\right)}^{-1}=6\mathit{\hspace{1em}\hspace{1em}}{\left(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\right)}^{-1}=2$$

e o circuito fica simplificado da forma seguinte:

Agora temos 3 condensadores em paralelo, entre os pontos B e D, e a capacidade equivalente é a capacidade do circuito entre os pontos B e D:

$$C_{\mathrm{BD}}=6+4+2=12\mathrm{pF}$$

(b) Se o medidor de capacidade for ligado entre os pontos A e B, o diagrama é o seguinte:

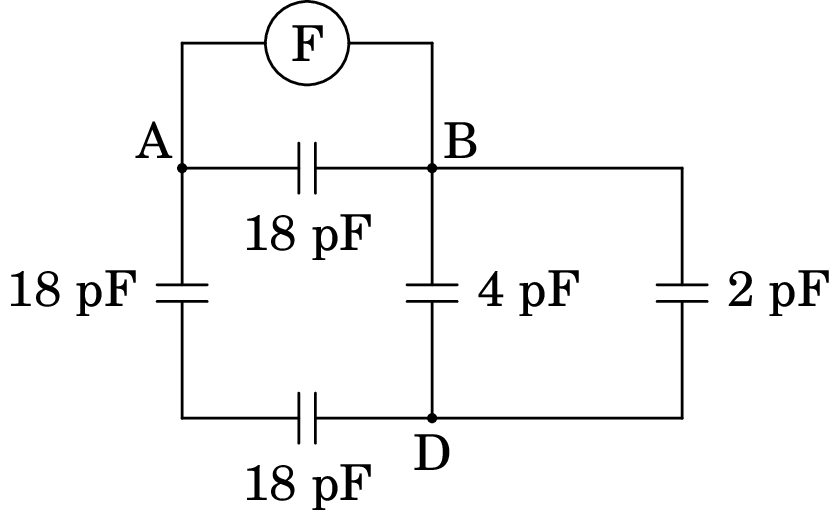
Os condensadores de 4 pF e 2 pF estão em paralelo, entre os pontos B e D, podendo ser substituídos por um único condensador de capacidade $4+2=6$ pF. O circuito obtido é o seguinte:

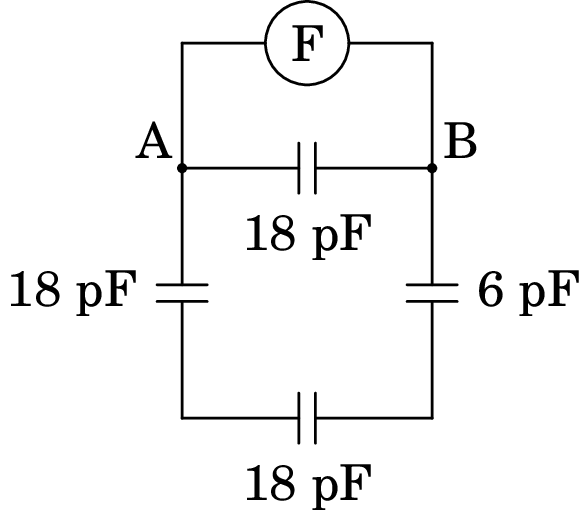
O condensador de 6 pF está agora em série com dois dos condensadores de 18 pF e a capacidade equivalente desse sistema em série é:

$${\left(\frac{1}{6}+\frac{1}{18}+\frac{1}{18}\right)}^{-1}=\frac{18}{5}=3.6\mathrm{pF}$$

e substituindo no diagrama anterior, obtém-se o seguinte circuito equivalente:

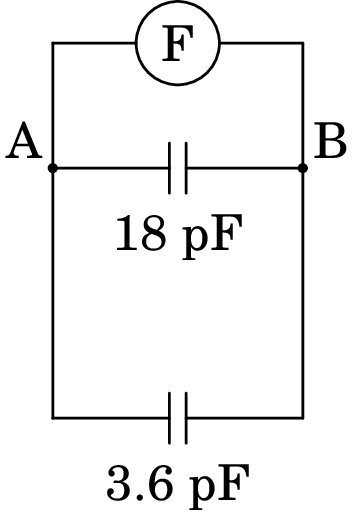
Finalmente, a capacidade entre os pontos A e B e a capacidade equivalente dos condensadores de 18 pF e 3.6 pF em paralelo:

$$C_{\mathrm{AB}}=18+3.6=21.6\mathrm{pF}$$

Problema 4.7

Dois condensadores de 10 nF e 15 nF ligam-se em série e estabelece-se uma diferença de potencial de 3 V entre os extremos do sistema.
(a) Determine a carga e a diferença de potencial em cada condensador.
(b) Os condensadores são separados, ligando-se de seguida os dois condensadores (armadura positiva com positiva e negativa com negativa). Calcule a voltagem e a carga final em cada condensador.

Resolução. O lado esquerdo da figura seguinte mostra os dois condensadores ligados em série e o lado direito mostra como serão ligados na alínea b.

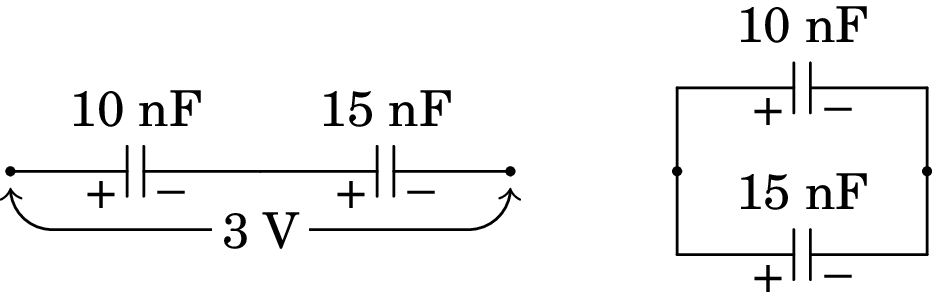
(a) Os dois condensadores em série são equivalentes a um único condensador com capacidade:

$$C_{\mathrm{s}}=\frac{10\times 15}{10+15}=6\mathrm{nF}$$

E a carga armazenada em cada um dos dois condensadores é a mesma carga no condensador equivalente:

$$Q=C_{\mathrm{s}}\mathrm{\Delta }V=18\mathrm{nC}$$

As diferenças de potencial nos dois condensadores são,

$$\mathrm{\Delta }{V}_{10}=\frac{18}{10}=1.8\mathrm{V}\mathit{\hspace{1em}\hspace{1em}}\mathrm{\Delta }{V}_{15}=\frac{18}{15}=1.2\mathrm{V}$$

(b) Como cada condensador tinha carga de 18 nC, quando se ligam entre sim, no lado onde há carga positiva ficarão 36 nC e no lado da carga negativa $-36$ nC. Essa carga distribuir-se há entre os dois condensadores, de forma a ficarem com a mesma diferença de potencial. Sendo $Q_{10}$ e $Q_{15}$ as cargas nos dois condensadores, temos então as seguintes duas condições:

$$Q_{10}+Q_{15}=36\mathit{\hspace{1em}\hspace{1em}}\mathrm{\Delta }V=\frac{Q_{10}}{10}=\frac{Q_{15}}{15}$$

e a solução dessas duas equações lineares é,

$$Q_{10}=14.4\mathrm{nC}\mathit{\hspace{1em}}{Q}_{15}=21.6\mathrm{nC}\mathit{\hspace{1em}}\mathrm{\Delta }V=1.44\mathrm{V}$$

Problema 4.8

Um condensador de 1.6 µF e voltagem máxima de 100 V liga-se em série com outro condensador de 2.5 µF e voltagem máxima de 150 V. Determine a voltagem máxima desse sistema.

Resolução. A voltagem máxima do sistema será a voltagem que faz com que em nenhum dos dois condensadores seja ultrapassada a sua voltagem máxima. A voltagem do sistema é a soma das voltagens $\mathrm{\Delta }{V}_1$ e $\mathrm{\Delta }{V}_2$ nos dois condensadores:

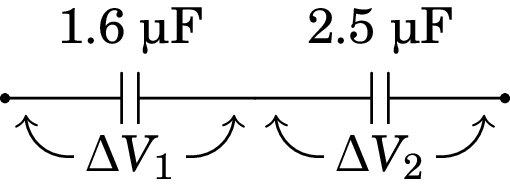
Se a voltagem $\mathrm{\Delta }{V}_1$ no condensador de 1.6 µF fossa a sua voltagem máxima de 100 V, a carga no sistema seria:

$$Q=100\times 1.6=160\mu \mathrm{C}$$

e a voltagem no condensador de 2.5 µF seria,

$$\mathrm{\Delta }{V}_2=\frac{160}{2.5}=64\mathrm{V}$$

que é um valor aceitável para o condensador de 2.5 µF. Já se a voltagem no condensador de 2.5 µF tivesse o seu valor máximo de 200 V, a carga no sistema seria:

$$Q=200\times 2.5=500\mu \mathrm{C}$$

e o condensador de 1.6 µF ficava com voltagem:

$$\mathrm{\Delta }{V}_1=\frac{250}{1.6}=156.25\mathrm{V}$$

que queimava esse condensador. Como tal, a voltagem máxima do sistema será 164 V, que faz com que os condensadores fiquem com voltagens de 100 V e 64 V.