1. Força elétrica

Problema 1.1

A unidade SI de carga elétrica é o coulomb (C). Mesmo para objetos do dia a dia, 1 C é uma carga elétrica enorme.
(a) Duas cargas, consideradas pontuais, de $1$ C cada estão à distância de $10$ cm. Calcule a força elétrica entre elas. Compare e comente o valor obtido com o peso de um Boeing $747$, considerando a sua massa como sendo de $180$ toneladas.
(b) Considere duas cargas elétricas iguais $q$ à distância de $10$ cm. Calcule o valor de $q$ de modo a que força entre as cargas seja de $100$ N. Comente o valor obtido.

Resolução. (a). Em unidades SI, a força entre as cargas é:

$$F=\frac{8.988\times {10}^9\times 1\times 1}{{0.1}^2}=8.99\times {10}^{11}\mathrm{N}$$

Usando o valor padrão da aceleração da gravidade, o peso do Boeing é

$$P=180\times {10}^3\times 9.807=1.77\times {10}^6\mathrm{N}$$

A força eléctrica seria equivalente ao peso de aproximadamente meio milhão de aviões Boeing 747.

(b) A partir da lei de Coulomb, com $q_1=q_2=q$, obtém-se:

$$q=\sqrt{\frac{F{d}^2}{k}}=\sqrt{\frac{100\times {0.1}^2}{8.988\times {10}^9}}=1.05\times {10}^{-5}\mathrm{C}=10.5\mu \mathrm{C}$$

Problema 1.2

Uma esfera de cobre possui um volume de $1$ dm${}^3$ e encontra-se eletricamente neutra. Dados do cobre: densidade volúmica de massa ${\rho }_{\mathrm{m}}=8.920$ g.cm${}^{-3}$, número atómico $Z=29$, massa atómica $A=63.546$.
(a) Calcule o número de eletrões existentes na esfera, bem como a sua carga.
(b) Caso o número de eletrões sofra uma variação de $1$%, determine a carga elétrica que a esfera adquire.
(c) Considerando agora uma segunda esfera idêntica à inicial, altera-se em cada uma o seu número de eletrões de $1$%. Calcule a força elétrica entre as esferas a uma distância de $15$ cm. Determine a massa duma esfera com peso igual a essa força e compare-a com a massa da Terra ($5.98\times {10}^{24}$ kg).
(d) Calcule o número de eletrões a serem removidos (injetados) de modo à esfera inicial ficar eletrizada positivamente (negativamente) com carga $1\mu$C (-$1\mu$C). Compare com o número total de eletrões inicial.
(e) Comente os resultados anteriores.

Resolução. (a) O número de eletrões $N_{\mathrm{e}}$ é igual ao número de átomos $N$ vezes o número atómico $Z$ (número de eletrões de um átomo neutro). O número de átomos $N$ calcula-se dividindo a massa da esfera, em gramas, pela massa de um átomo, em gramas (massa atómica dividida pelo número de Avogadro):

$$N_{\mathrm{e}}=\frac{8.920\times {10}^3}{63.546/6.022\times {10}^{23}}\times 29=2.451\times {10}^{27}$$

e a carga desses eletrões obtém-se multiplicando pela carga elementar, com sinal negativo:

$$Q=-2.451\times {10}^{27}\times 1.602\times {10}^{-19}=-3.93\times {10}^8\mathrm{C}$$

(b) A esfera adquire carga positiva igual a 0.01 vezes o valor absoluto da carga dos eletrões calculada na alínea anterior, ou seja, fica com carga $3.93\times {10}^6$ C.

(c) Como será explicado num capítulo posterior, a força entre esferas com carga distribuída uniformemente pode ser calculada admitindo cargas pontuais concentradas no centro das esferas. Usando a lei de Coulomb para duas cargas pontuais iguais à que foi calculada na alínea anterior

$$F=\frac{8.988\times {10}^9\times {(3.93\times {10}^6)}^2}{{0.15}^2}=6.17\times {10}^{24}\mathrm{N}$$

A massa de uma esfera que tivesse esse peso seria,

$$m=\frac{6.17\times {10}^{24}}{9.807}=6.29\times {10}^{23}\mathrm{kg}$$

E a sua relação com a massa da Terra é

$$\frac{m}{M}=\frac{6.29\times {10}^{23}}{5.98\times {10}^{24}}=0.11$$

ou seja, a massa é 11 % da massa da Terra.

(d) O número de eletrões que deve ser removido é a carga pretendida dividida pela carga elementar:

$$\mathrm{\Delta }{N}_{\mathrm{e}}=\frac{1\times {10}^{-6}}{1.602\times {10}^{-19}}=6.242\times {10}^{12}$$

e comparando com o número de eletrões calculado na alínea a,

$$\frac{\mathrm{\Delta }{N}_{\mathrm{e}}}{N_{\mathrm{e}}}=\frac{6.242\times {10}^{12}}{2.451\times {10}^{27}}=2.55\times {10}^{-15}=2.55\times {10}^{-13}\%$$

(e) A carga elétrica dos eletrões de um objeto macroscópico é gigantesca ($\sim {10}^8$ C), mas como a carga elétrica dos protões é igual e de sinal oposto, um objeto do dia-a-dia encontra-se normalmente neutro. A variação de 1 % do número de eletrões provocaria uma carga macroscópica enorme ($\sim {10}^6$ C). Para termos um carga macroscópica típica ($1$ $\mu$C), é suficiente uma variação muitíssimo pequena do número de eletrões ($2.55\times {10}^{-13}$ %).

Problema 1.3

Determine a força elétrica resultante sobre cada uma das cargas representadas na figura.

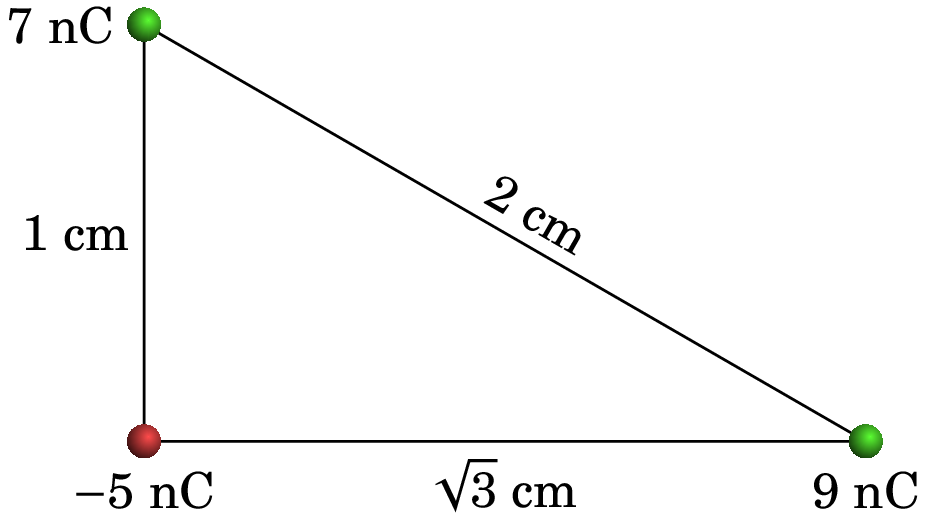
Resolução. A figura seguinte mostra os três diagramas de forças para as três partículas, admitindo que a carga $q_1$ é a de $-5$ nC, a carga $q_2$ é a de 9 nC e $q_3$ é a de 7 nC.

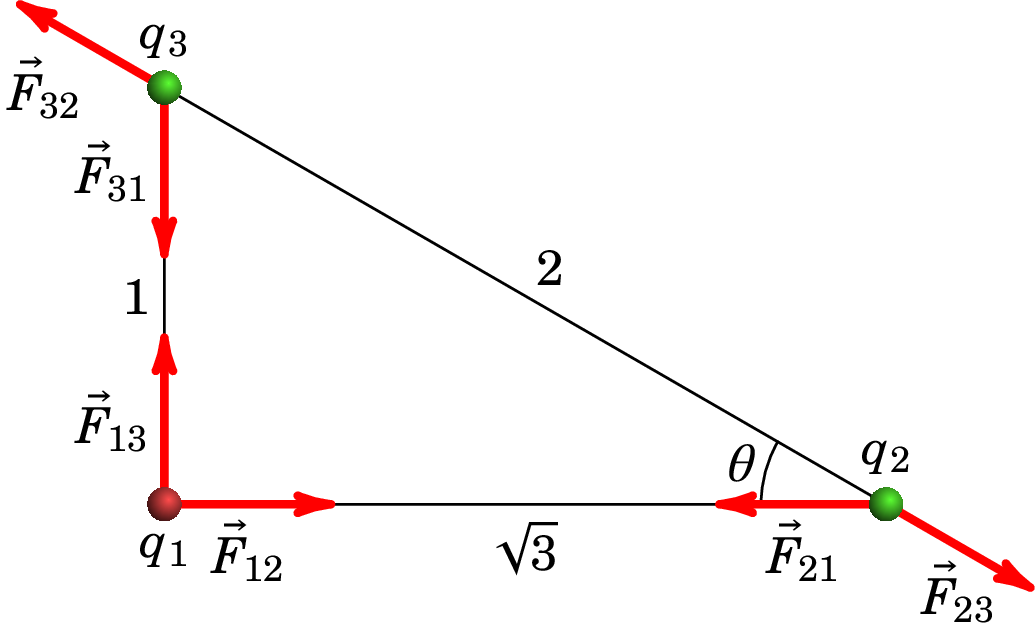
Em cada vetor ${\overrightarrow{F}}_{ij}$ o primeiro índice $i$ indica o número da carga onde a força atua, e o segundo índice $j$ é o número da carga que produz essa força. As forças elétricas verificam a lei de ação e reação: ${\overrightarrow{F}}_{ij}=-{\overrightarrow{F}}_{ji}$, e em módulo, $F_{ij}=F_{ji}$.

Para facilitar as contas, convém manter as unidades dadas para as cargas (nC) e as distâncias (cm) e mudar o valor da constante $k$ para essas unidades:

$$k=8.988\times {10}^9\frac{\mathrm{N}\cdot {\mathrm{m}}^2}{{\mathrm{C}}^2}=8.988\times {10}^9\frac{\mathrm{N}\cdot {\left({10}^2\mathrm{cm}\right)}^2}{{\left({10}^9\mathrm{nC}\right)}^2}=0.08988\frac{\mathrm{mN}\cdot {\mathrm{cm}}^2}{{\mathrm{nC}}^2}$$

Se usarmos $k=0.08988$, com cargas em nC e distâncias em cm, as forças obtidas estarão em mN. A lei de Coulomb permite calcular os módulos das seis forças na figura acima:

$F_{12}$ $={\displaystyle \frac{0.08988\times 5\times 9}{3}}=1.3482\mathrm{mN}$

$F_{13}$ $={\displaystyle \frac{0.08988\times 5\times 7}{1}}=3.1458\mathrm{mN}$

$F_{23}$ $={\displaystyle \frac{0.08988\times 9\times 7}{4}}=1.4156\mathrm{mN}$

Observando a figura, conclui-se que o cosseno e o seno do ângulo $\theta$ são:

$$\cos \theta =\frac{\sqrt{3}}{2}\mathit{\hspace{1em}\hspace{1em}}\sin \theta =\frac{1}{2}$$

Fixando o eixo dos $x$ de $q_1$ para $q_2$ e o eixo dos $y$ de $q_1$ para $q_3$, as forças resultantes, ${\overrightarrow{F}}_i$, sobre cada uma das três cargas obtêm-se observando o diagrama das forças:

${\overrightarrow{F}}_1$ $=F_{12}\hat{ı}+F_{13}\hat{ȷ}=\left(1.35\hat{ı}+3.15\hat{ȷ}\right)\mathrm{mN}$

${\overrightarrow{F}}_2$ $=(F_{23}\cos \theta -F_{21})\hat{ı}-F_{23}\sin \theta \hat{ȷ}=\left(-0.122\hat{ı}-0.708\hat{ȷ}\right)\mathrm{mN}$

${\overrightarrow{F}}_3$ $=-F_{32}\cos \theta \hat{ı}+(F_{32}\sin \theta -F_{31})\hat{ȷ}=\left(-1.23\hat{ı}-2.44\hat{ȷ}\right)\mathrm{mN}$

Problema 1.4

Três cargas pontuais estão ligadas por dois fios isoladores de 2.65 cm cada (ver figura). Calcule a tensão em cada fio.

Resolução. Tal como no problema anterior, usaremos $k=0.08988$, as cargas em nC e as distâncias em cm; as forças assim obtidas estarão em mN.

Sobre cada uma das partículas atuam forças elétricas e tensões nos fios aos que estejam ligadas. Como este sistema está em equilíbrio, a força resultante sobre cada uma das 3 partículas deverá ser nula. Como tal, temos 3 condições de equilíbrio com apenas 2 incógnitas, que são as tensões nos dois fios.

Basta então considerar apenas as condições de equilíbrio para duas das partículas. Os diagramas de forças para as cargas de 3.2 nC e 7.4 nC (designadas de $q_1$ e $q_3$) são os seguintes:

onde $T_a$ é a tensão no fio do lado esquerdo e $T_b$ a tensão no fio do lado direito. Observe-se que $q_1$ não está em contacto com o fio da direita e, por isso, ${\overrightarrow{T}}_b$ não atua sobre essa partícula. De forma análoga para $q_3$. No entanto, as forças elétricas atuam à distância, sem ter de existir contacto entre as partículas; sobre cada uma das 3 partículas atuam as forças elétricas produzidas pelas outras duas partículas.

A condição de equilíbrio para a carga $q_1$ é

$$T_a=F_{12}+F_{13}$$

Como tal, a tensão no fio do lado esquerdo é (unidades SI):

$$T_a=0.08988\left(\frac{3.2\times 5.1}{{2.65}^2}+\frac{3.2\times 7.4}{{(2\times 2.65)}^2}\right)=0.285\mathrm{mN}=285\mu \mathrm{N}$$

A condição de equilíbrio para a carga $q_3$ é

$$T_b=F_{31}+F_{32}$$

que conduz à tensão no fio do lado direito:

$$T_b=0.08988\left(\frac{7.4\times 5.1}{{2.65}^2}+\frac{7.4\times 3.2}{{(2\times 2.65)}^2}\right)=0.559\mathrm{mN}=559\mu \mathrm{N}$$

Se tivéssemos optado por usar a condição de equilíbrio para a partícula $q_2$, no diagrama das forças há que ter em conta que atuam as tensões dos dois fios, porque essa partícula está em contacto com os dois fios:

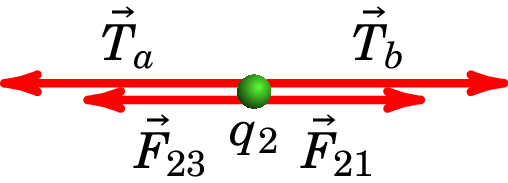
E a respetiva condição de equilíbrio é

$$T_a+F_{23}=T_b+F_{21}$$

equação essa que podia ter sido resolvida em simultâneo com alguma das duas equações para $q_1$ ou $q_3$, obtendo-se a mesma resposta, já que esta terceira condição obtém-se subtraindo as duas primeiras condições, e tendo em conta que para quaisquer índices $i$ e $j$, $F_{ij}$ é igual a $F_{ji}$.

Problema 1.5

A soma dos valores de duas cargas pontuais $q_1$ e $q_2$ é $q_1+q_2=10$ µC. Quando estão afastadas 3 m entre si, o módulo da força exercida por cada uma delas sobre a outra é 24 mN. Determine os valores de $q_1$ e $q_2$, se: (a) Ambas cargas são positivas. (b) Uma das cargas é positiva e a outra negativa.

Resolução. Para poder usar os números simples do enunciado (10 e 3), usaremos as mesmas unidades do enunciado: cargas em µC, distâncias em metros e forças em mN. Como tal, o valor que usaremos para a constante de Coulomb será:

$$k=8.988\times {10}^9\frac{\mathrm{N}\cdot {\mathrm{m}}^2}{{\mathrm{C}}^2}=8.988\times {10}^9\frac{{10}^3\mathrm{mN}\cdot {\mathrm{m}}^2}{{10}^{12}\mu {\mathrm{C}}^2}=8.988\frac{\mathrm{mN}\cdot {\mathrm{m}}^2}{\mu {\mathrm{C}}^2}$$

A primeira condição, nas unidades escolhidas, é:

$$q_1+q_2=10$$

Observe-se que $q_1$ e $q_2$ poderão ter valores positivos ou negativos.

(a) Se as duas cargas são positivas, o produto entre elas, $q_1{q}_2$, também é positivo. Como tal, na lei de Coulomb o produto dos valores absolutos das cargas pode ser substituído pelo produto das cargas: $|q_1||q_2|=q_1{q}_2$, e a condição para que o módulo da força seja 24 mN é:

$$\frac{8.988q_1{q}_2}{9}=24$$

Substituindo $q_2$ por $10-q_1$ nesta equação, obtém-se a equação quadrática:

$$8.988q_1^2-89.88q1+216=0$$

e a fórmula resolvente para equações quadráticas conduz aos valores das duas cargas:

$$q_1=4.02\mu \mathrm{C}\mathit{\hspace{1em}\hspace{1em}}{q}_2=5.98\mu \mathrm{C}$$

As duas cargas aparecem como possíveis soluções para $q_1$, porque a designação de qual das partículas é a 1 e qual a 2 é arbitrária.

(b) Quando os sinais das cargas são opostos, $q_1{q}_2$ será negativo. Como tal, o produto dos valores absolutos deverá ser substituído por: $|q_1||q_2|=-q_1{q}_2$, e a condição para a força é

$$-\frac{8.988q_1{q}_2}{9}=24$$

Substituindo $q_2$ por $10-q_1$ nesta equação, obtém-se a equação quadrática:

$$8.988q_1^2-89.88q1-216=0$$

e as duas cargas são:

$$q_1=-2.00\mu \mathrm{C}\mathit{\hspace{1em}\hspace{1em}}{q}_2=12.00\mu \mathrm{C}$$

Problema 1.6

Duas pequenas esferas condutoras, com cargas $q_1=+300$ nC e $q_2=+500$ nC, e com a mesma massa $m$, são coladas a dois fios isoladores, cada um com 8 cm de comprimento. Os fios são logo colados numa barra horizontal, em dois pontos a uma distância $d=15$ cm entre si. A repulsão eletrostática entre as cargas faz com que os dois fios se inclinem um ângulo $\theta ={10}^{\circ }$ em relação à vertical. Determine o valor da massa $m$.

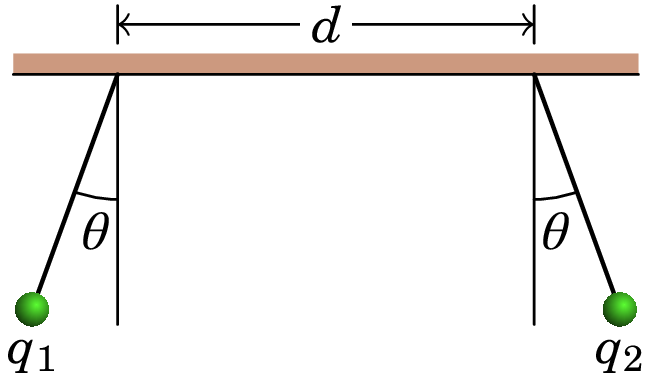
Resolução. Os diagramas de corpo livre das duas esferas são os seguintes:

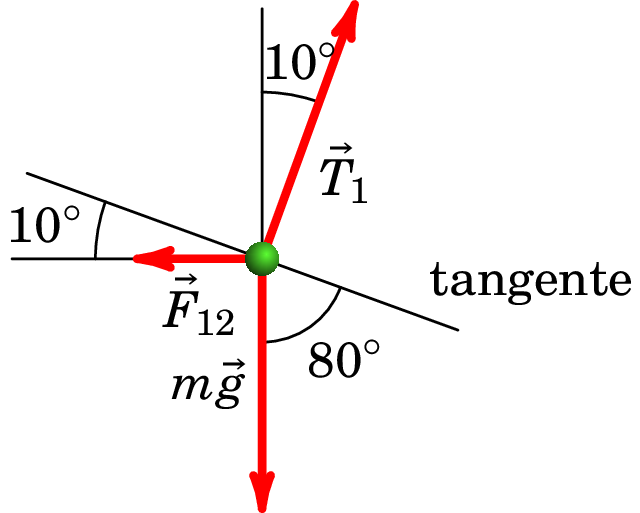
onde ${\overrightarrow{T}}_1$ e ${\overrightarrow{T}}_2$ são as tensões nos dois fios, ${\overrightarrow{F}}_{12}$ é a força elétrica da esfera 2 sobre a esfera 1 e ${\overrightarrow{F}}_{21}$ é a força elétrica da esfera 1 sobre a esfera 2.

Realmente basta um dos diagramas para determinar o valor de $m$. E como a soma das 3 forças externas sobre cada esfera é nula, por estarem em repouso, e os módulos das forças elétricas ${\overrightarrow{F}}_{21}$ e ${\overrightarrow{F}}_{12}$ são iguais, os módulos das duas tensões são iguais e os dois diagramas são equivalentes.

A distância entre as duas esferas (em metros) é,

$$r=0.15+2\times 0.08\times \sin ({10}^{\circ })=0.17778$$

E, usando a lei de Coulomb,

$$F_{21}=F_{12}=\frac{8.988\times {10}^9\times 3\times {10}^{-7}\times 5\times {10}^{-7}}{{0.17778}^2}=0.042657\mathrm{N}$$

A soma das 3 forças igual a zero implica que a soma das suas componentes, ao longo de qualquer direção, é nula. Em particular, a soma das componentes na direção tangente indicada na figura é igual a:

$mg\cos ({80}^{\circ })-F_{12}\cos ({10}^{\circ })=0$

$m={\displaystyle \frac{F_{12}\cos ({10}^{\circ })}{g\cos ({80}^{\circ })}}={\displaystyle \frac{0.042657\cos ({10}^{\circ })}{9.807\cos ({80}^{\circ })}}=0.0247\mathrm{kg}$

A massa das esferas é de $24.7$ gramas.

Problema 1.7

Quatro cargas pontuais $q_1=-12\mathrm{nC}$, $q_2=-5\mathrm{nC}$, $q_3=9\mathrm{nC}$ e $q_4=27\mathrm{nC}$ encontram-se nos vértices de um tetraedro regular de aresta $d=21\mathrm{cm}$. Determine o módulo da força resultante sobre a carga $q_4$.

Resolução. Os três eixos coordenados podem ser escolhidos como mostra a figura seguinte, com a carga $q_3$ na origem, a carga $q_2$ no eixo dos $x$ e a carga $q_1$ sobre o plano $xz$.

Como tal, os vetores posição de $q_3$ e $q_2$ são

$${\overrightarrow{r}}_3=\overrightarrow{0}\mathit{\hspace{1em}\hspace{1em}}{\overrightarrow{r}}_2=d\hat{ȷ}$$

A figura seguinte mostra as três cargas $q_1$, $q_2$ e $q_3$ no plano $xy$, nos vértices dum triângulo equilátero de aresta $d$.

O vetor posição da carga $q_1$ é então,

$${\overrightarrow{r}}_1=\frac{d}{2}\left(\sqrt{3}\hat{ı}+\hat{ȷ}\right)$$

Na figura anterior, o ponto P encontra-se a uma distância $\sqrt{3}d/6$ do eixo dos $y$ e a uma distância $\sqrt{3}d/3$ de $q_1$. A carga $q_4$ encontrar-se-á por cima do ponto P. A figura seguinte mostra o ponto P e as cargas $q_1$ e $q_4$, com uma distância $d$ entre elas.

A altura desse triângulo retângulo é

$$\sqrt{d^2-\frac{3}{9}{d}^2}=\frac{\sqrt{6}}{3}d$$

Como tal, o vetor posição da carga $q_4$ é

$${\overrightarrow{r}}_4=d\left(\frac{\sqrt{3}}{6}\hat{ı}+\frac{1}{2}\hat{ȷ}+\frac{\sqrt{6}}{3}\hat{k}\right)$$

Os três versores que determinam a direção de $q_4$ relativa a cada uma das outras três cargas são:

${\hat{r}}_{4/1}$ $=-{\displaystyle \frac{\sqrt{3}}{3}}\hat{ı}+{\displaystyle \frac{\sqrt{6}}{3}}\hat{k}$

${\hat{r}}_{4/2}$ $={\displaystyle \frac{\sqrt{3}}{6}}\hat{ı}-{\displaystyle \frac{1}{2}}\hat{ȷ}+{\displaystyle \frac{\sqrt{6}}{3}}\hat{k}$

${\hat{r}}_{4/3}$ $={\displaystyle \frac{\sqrt{3}}{6}}\hat{ı}+{\displaystyle \frac{1}{2}}\hat{ȷ}+{\displaystyle \frac{\sqrt{6}}{3}}\hat{k}$

As 3 forças elétricas sobre a partícula 4 calculam-se a partir da lei de Coulomb e a força resultante é a soma dessas 3 forças

$${\overrightarrow{F}}_4=\frac{k{q}_4}{d^2}(q_1{\hat{r}}_{4/1}+q_2{\hat{r}}_{4/2}+q_3{\hat{r}}_{4/3})$$

Como a aresta do tetraedro é dada em centímetros, convém usar a constante $k$ nas unidades seguintes:

$$k=89.88\frac{\mu \mathrm{N}\cdot {\mathrm{cm}}^2}{{\mathrm{nC}}^2}$$

O resultado obtido para a força sobre a partícula 4 é

$${\overrightarrow{F}}_4=5.5029\left(\frac{14\sqrt{3}}{3}\hat{ı}+7\hat{ȷ}-\frac{8\sqrt{6}}{3}\hat{k}\right)\mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}{F}_4=69.0\mu \mathrm{N}.$$

Problema 1.8

Um eletrão desloca-se no sentido positivo do eixo dos $x$ sob a ação de um campo elétrico. A expressão da sua velocidade é $1300{\mathrm{e}}^{-3x}$, onde a coordenada $x$ é dada em metros e a velocidade em m/s. Determine a expressão do campo elétrico $E_x$, ao longo do eixo dos $x$, em N/C (a massa dum eletrão é $9.109\times {10}^{-31}$ kg).

Resolução. A partir da expressão da velocidade encontra-se a expressão para a aceleração em função de $x$

$a$ $={\displaystyle \frac{\mathrm{d}v}{\mathrm{d}t}}={\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}=v{\displaystyle \frac{\mathrm{d}v}{\mathrm{d}x}}=1300{\mathrm{e}}^{-3x}\left(-3900{\mathrm{e}}^{-3x}\right)$

$=-507\times {10}^4{\mathrm{e}}^{-6x}$

E a expressão do campo elétrico é:

$E$ $={\displaystyle \frac{F}{q}}=-{\displaystyle \frac{ma}{e}}={\displaystyle \frac{9.109\times {10}^{-31}\times 507\times {10}^4}{1.602\times {10}^{-19}}}{\mathrm{e}}^{-6x}$

$=28.8\times {10}^{-6}{\mathrm{e}}^{-6x}\left({\displaystyle \frac{\mathrm{N}}{\mathrm{C}}}\right)$

Observe-se que o eletrão desloca-se no sentido positivo do eixo dos $x$ e o campo também aponta nesse sentido. A carga negativa do eletrão implica força no sentido oposto (aceleração no sentido negativo do eixo dos $x$), que faz abrandar o eletrão de forma que a sua velocidade aproxima-se assimptoticamente de 0.