5. Força eletromotriz, corrente e resistência

Problema 5.1

Determine o trabalho realizado por uma pilha de 9 V, que fornece uma corrente de 235 mA durante 5 minutos.

Resolução. A potência fornecida pela pilha é:

$$P=\epsilon I=9\times 235\times {10}^{-3}=2.115\mathrm{W}$$

e o trabalho realizado é igual à energia fornecida durante os 5 minutos:

$$W=\mathrm{\Delta }U=P\mathrm{\Delta }t=2.115\times 5\times 60=634.5\mathrm{J}$$

Problema 5.2

Uma certa bateria de automóvel tem carga máxima de 250 Ah, que corresponde à carga disponível quando está carregada a 100%.
(a) Depois de algum uso, a bateria descarrega até 60% da sua carga máxima. Qual é a carga, em coulomb, com que fica a bateria?
(b) A seguir, a bateria liga-se a um carregador de 12 V para a recarregar e observa-se que inicialmente a corrente do carregador tem intensidade de 7 A, mas 6 horas depois diminui a 3 A. Admitindo diminuição linear da corrente em ordem ao tempo, com que percentagem da sua carga máxima fica a bateria no fim das 6 horas?

Resolução. (a) Após ter descarregado pelo uso, a carga restante na bateria é 60% da sua carga máxima inicial de 250 A·h, a qual em coulomb é igual a:

$$Q=0.6\times 250\times 3600=5.4\times {10}^5\mathrm{C}$$

(b) Como a corrente diminui linearmente, a corrente média durante as 6 horas é a média entre a corrente inicial e final:

$$\overline{I}=\frac{7+3}{2}=5\mathrm{A}$$

A carga transferida para a bateria pelo carregador, durante as 6 horas, é igual à corrente média vezes o tempo:

$$\mathrm{\Delta }Q=(5\mathrm{A})\times (6\mathrm{h})=30\mathrm{A}\cdot \mathrm{h}$$

e como a bateria descarregada tinha carga de $0.6\times 250$ A·h $=150$ A·h, a carga final dividida pela inicial será:

$$\frac{Q_{\mathrm{f}}}{Q_{\mathrm{i}}}=\frac{150+30}{250}=0.72$$

Ou seja, a bateria fica com 72% da sua carga inicial.

Comentário: Também podíamos ter determinado a carga transferida para a bateria encontrando a equação da reta correspondente a 7 A em $t=0$ e 3 A em $t=6$ (tempo medido em horas), a qual é dada por:

$$I(t)=7-\frac{2}{3}t$$

E a carga transferida é o integral dessa expressão, entre 0 e 6 horas:

$$\mathrm{\Delta }Q={\int }_0^6\left(7-\frac{2}{3}t\right)dt=30\mathrm{A}\cdot \mathrm{h}$$

Note também que o valor médio da corrente elétrica é o integral da equação da reta, de 0 a 6, dividido pelo comprimento do intervalo de integração (6 horas).

$$\overline{I}=\frac{1}{6}{\int }_0^6\left(7-\frac{2}{3}t\right)dt=5\mathrm{A}$$

Problema 5.3

A corrente num cabo varia de acordo com a função $I=20+3t^2$, onde $I$ mede-se em miliampere e $t$ em segundos.
(a) Que carga transporta o cabo desde $t=0$ até $t=10$ s?
(b) Qual o valor da corrente constante que transporta a mesma quantidade de carga no mesmo intervalo de tempo?

(a) A carga transferida é igual ao integral da corrente, em ordem ao tempo, no intervalo de tempo em questão:

$$\mathrm{\Delta }Q={\int }_0^{10}\left(20+3t^2\right)dt=1200$$

As unidades de $I$ eram mA e as unidades de $\mathrm{d}t$ segundos. Como tal, o resultado está em mA·s que são mC. A carga transferida é então $\mathrm{\Delta }Q=1.2$ C.

(b) A corrente média nesse intervalo é $\mathrm{\Delta }Q/10$, ou seja, seria necessária uma corrente constante de 120 mA para transferir a mesma carga nos mesmos 10 segundos.

Problema 5.4

Num condutor ligado a uma pilha com f.e.m. de 1.5 V, circulam $9.6\times {10}^{21}$ eletrões de condução durante 2 horas. Determine:
(a) A intensidade da corrente média.
(b) A energia fornecida pela pilha durante esse intervalo.
(c) A potência média fornecida pela pilha.
(d) Se a carga inical da pilha era de 3 A·h, com que carga fica após as 2 horas?

Resolução. (a) O valor absoluto da carga transferida é o número de eletrões transferidos vezes a carga elementar. A corrente média, em ampere, é a carga transferida, em Coulomb, dividida pelo tempo, em segundos:

$$\overline{I}=\frac{9.6\times {10}^{21}\times 1.602\times {10}^{-19}}{7200}=214\mathrm{mA}$$

(b) A energia fornecida é igual à carga transferida, vezes a força eletromotriz:

$$E_{\mathrm{p}}=9.6\times {10}^{21}\times 1.602\times {10}^{-19}\times 1.5=2307\mathrm{J}$$

(c) A potência média fornecida é igual ao produto entre força eletromotriz (constante) e a corrente média (ou, também, energia fornecida dividida pelo intervalo de tempo):

$$\overline{P}=1.5\overline{I}=0.320\mathrm{W}$$

(d) A carga final é igual à carga inicial, menos a carga transferida durante as 2 horas. Em unidades de A·h, a carga transferida é igual à corrente média, em ampere, vezes o intervalo de tempo, em horas:

$$Q_{\mathrm{f}}=3-2\overline{I}=2.573\mathrm{A}\mathrm{·}\mathrm{h}$$

Problema 5.5

No circuito da figura, determine a resistência equivalente:
(a) entre B e D,
(b) entre A e B,
(c) entre A e D

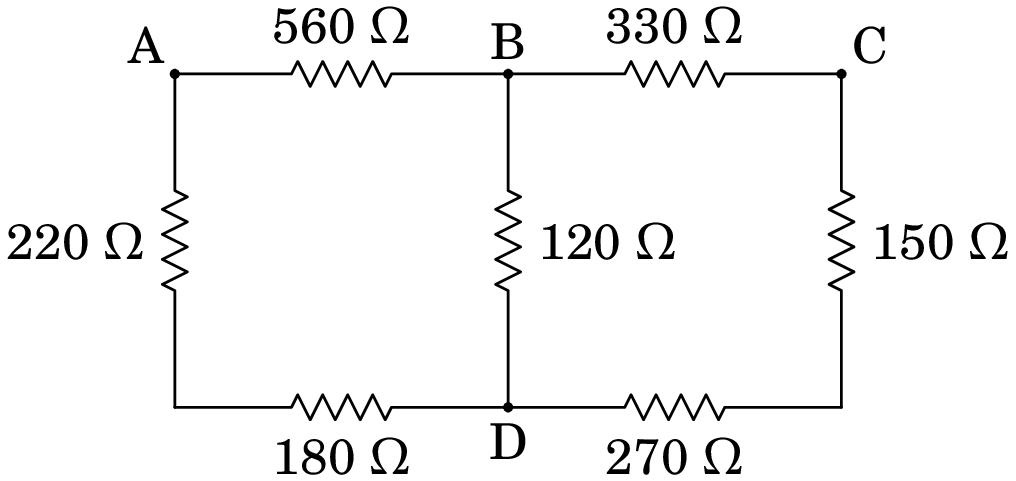
Resolução.(a) Para determinar a resistência entre B e D, admitimos que há um medidor de resistências ligado nesses pontos, mas não há nada ligado nos pontos A e C. Como tal, as correntes nas resistências de 560 $\mathrm{\Omega }$, 220 $\mathrm{\Omega }$ e 180 $\mathrm{\Omega }$ são iguais e, como tal, essas 3 resistências estão em série, podendo ser substituídas por uma única resistência de 960 $\mathrm{\Omega }$. De forma análoga, as correntes nas resistências de 330 $\mathrm{\Omega }$, 150 $\mathrm{\Omega }$ e 270 $\mathrm{\Omega }$ são iguais e, podendo ser substituídas por uma única resistência de 750 $\mathrm{\Omega }$. Com essas duas substituições obtém-se o seguinte circuito equivalente:

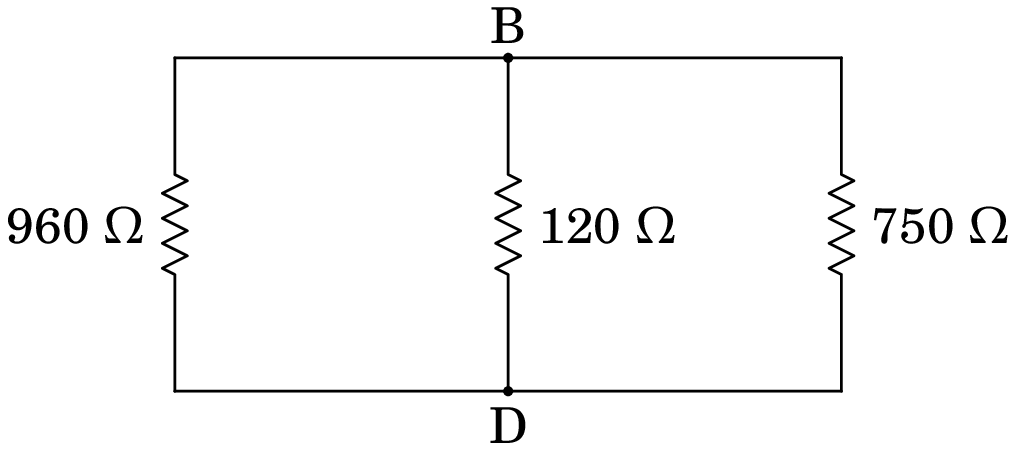
Cada uma das três resistências nesse circuito está ligada entre os pontos B e D. Como tal, as três resistências estão em paralelo e a resistência equivalente entre B e D é:

$$R={\left(\frac{1}{960}+\frac{1}{120}+\frac{1}{750}\right)}^{-1}=93.39\mathrm{\Omega }$$

(b) Para determinar a resistência entre A e B, as resistências de 220 $\mathrm{\Omega }$ e 180 $\mathrm{\Omega }$ estão em série (equivalente a 400 $\mathrm{\Omega }$), mas não estão em série com a de 560 $\mathrm{\Omega }$, porque em A entra ou sai corrente para o medidor de resistência. As resistências de 330 $\mathrm{\Omega }$, 150 $\mathrm{\Omega }$ e 270 $\mathrm{\Omega }$ também estão em série, porque não há nada ligado em C, sendo equivalentes a uma única resistência de 750 $\mathrm{\Omega }$:

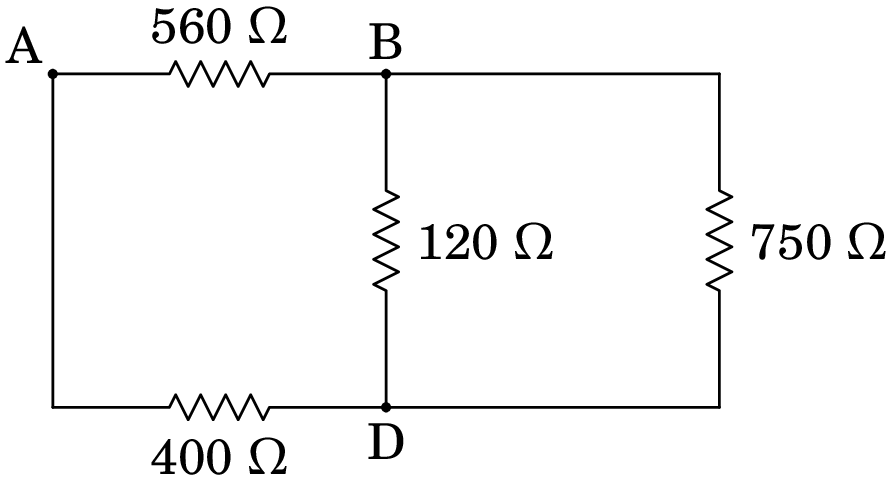
As resistências de 120 $\mathrm{\Omega }$ e 750 $\mathrm{\Omega }$, que estão em paralelo, podem ser substituídas pela resistência equivalente,

$${\left(\frac{1}{120}+\frac{1}{750}\right)}^{-1}=\frac{120\times 750}{120+750}=\frac{3000}{29}\mathrm{\Omega }$$

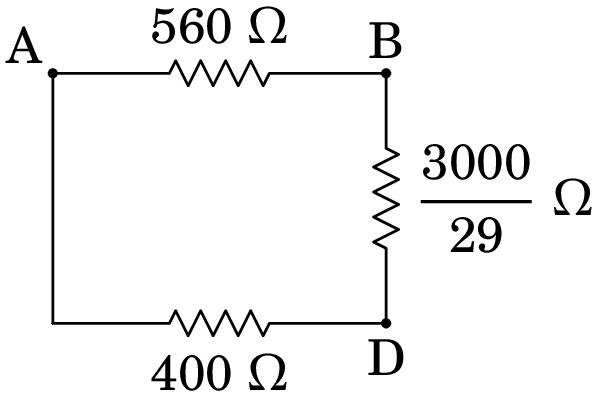
As resistências de 400 $\mathrm{\Omega }$ e 3000/29 $\mathrm{\Omega }$, em série porque não há nada ligado em D, são equivalentes a 14600/29 $\mathrm{\Omega }$

E essas duas resistências estão em paralelo, sendo a resistência equivalente entre A e B igual a:

$$R={\left(\frac{1}{560}+\frac{29}{14600}\right)}^{-1}=265.1\mathrm{\Omega }$$

(c) Para determinar a resistência equivalente entre A e D, podem-se usar os mesmos dois primeiros passos da alínea anterior, conduzindo ao circuito equivalente:

As resistências de 560 $\mathrm{\Omega }$ e 3000/29 $\mathrm{\Omega }$, em série porque não há nada ligado em B, são equivalentes a 19240/29 $\mathrm{\Omega }$

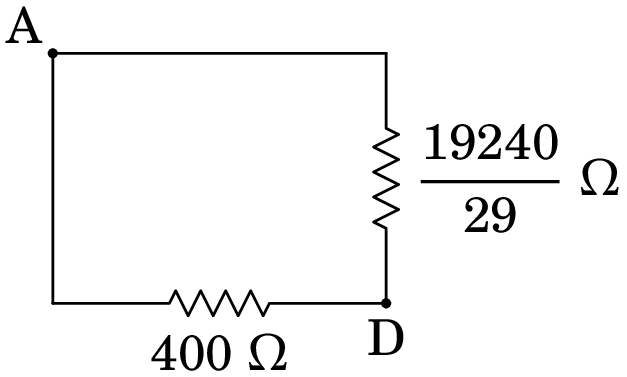
Finalmente, essas duas resistências estão em paralelo e a resistência equivalente entre A e D é:

$$R={\left(\frac{1}{400}+\frac{29}{19240}\right)}^{-1}=249.5\mathrm{\Omega }$$

Comentário: O método usado aqui não poderia ser usado para encontrar a resistência equivalente entre A e C. O único que poderíamos fazer seria combinar as resistências de 220 $\mathrm{\Omega }$ e 180 $\mathrm{\Omega }$ em série, e as resistências de 150 $\mathrm{\Omega }$ e 270 $\mathrm{\Omega }$ em série. Mas a seguir fica-se com um circuito em que nenhumas das resistências estão ou em série ou em paralelo. Nesse caso pode usar-se uma transformação delta-estrela, que será explicada no capítulo 6.

Problema 5.6

Determine a corrente e a diferença de potencial em cada resistência:

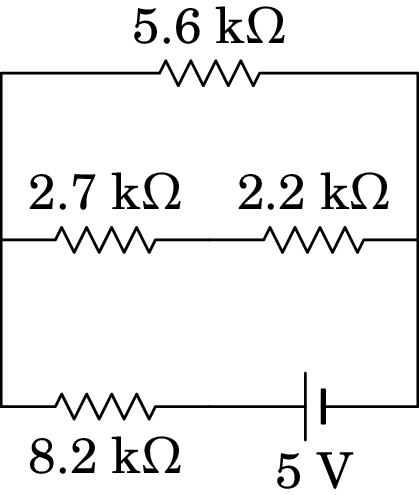
Resolução. As quatro resistências podem ser combinadas numa só, usando os três passos indicados na figura seguinte. Primeiro combinam-se as resistências de 2.7 k$\mathrm{\Omega }$ e 2.2 k$\mathrm{\Omega }$, em série, a seguir a resultante combina-se, em paralelo, com a resistência de 5.6 k$\mathrm{\Omega }$ e a resultante combina-se em série com a resistência de 8.2 k$\mathrm{\Omega }$.

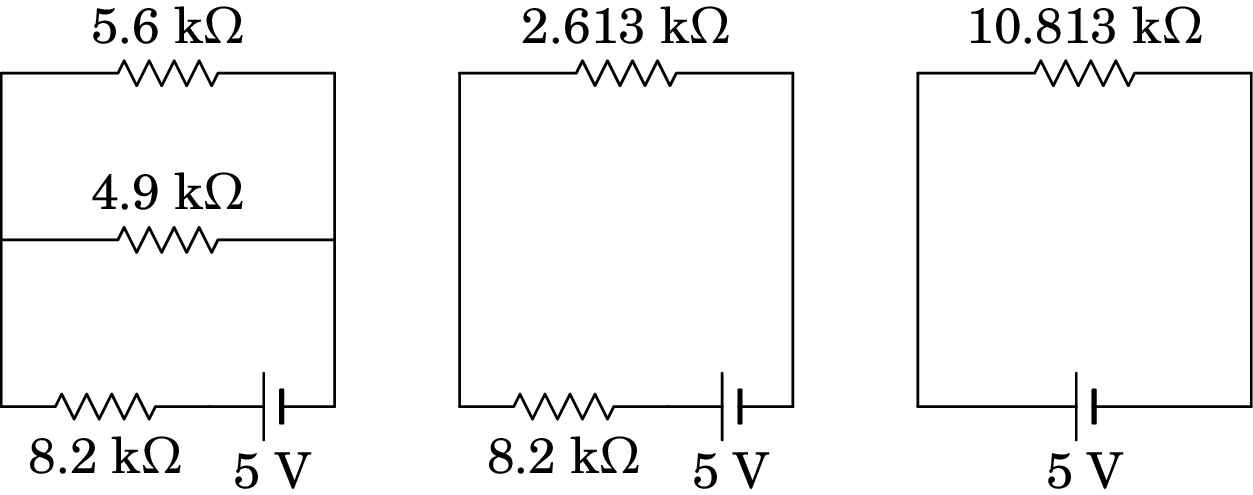
Com uma única resistência ligada à f.e.m. de 5 V, a diferença de potencial nessa resistência são 5 V e a corrente é:

$$I=\frac{\mathrm{\Delta }V}{R}=\frac{5}{10813}=462\mu \mathrm{A}$$

Substituindo a resistência de 10.813 k$\mathrm{\Omega }$ pelas resistências de 2.613 k$\mathrm{\Omega }$ e 8.2 k$\mathrm{\Omega }$ em série, como mostra a figura seguinte, a corrente de 462 µA será igual nas duas e as diferenças de potencial serão essa corrente multiplicada pelas duas resistências.

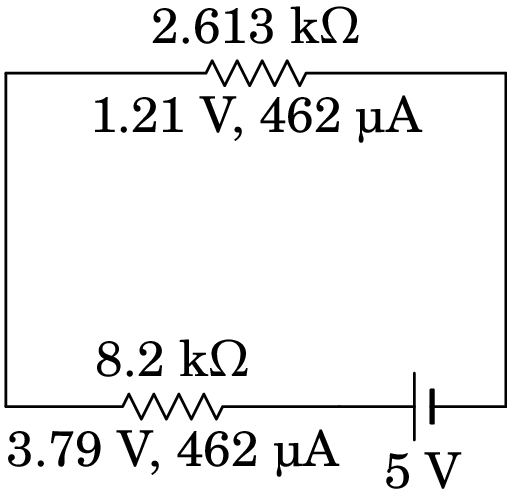
Observe-se que os resultados das diferenças de potencial foram ambos arredondados a duas casas decimais e de forma a que a soma deles seja igual aos 5 V da f.e.m.

Substituindo a resistência de 2.613 k$\mathrm{\Omega }$ pelas resistências de 5.6 k$\mathrm{\Omega }$ e 4.9 k$\mathrm{\Omega }$ em paralelo, a diferença de potencial nessas duas resistências em paralelo será a mesma, 1.21 V, e as correntes nas duas resistências obtêm-se usando a lei de Ohm:

$I_1={\displaystyle \frac{1.21}{5600}}=216.07\mu \mathrm{A}$

$I_2={\displaystyle \frac{1.21}{4900}}=246.94\mu \mathrm{A}$

Arredondando as correntes para números inteiros, de forma consistente com o circuito anterior, usaremos 216 e 246 como mostra a figura seguinte (a soma deverá ser 462 e 246.94 está mais próximo de 246 do que 216.07 em relação a 215).

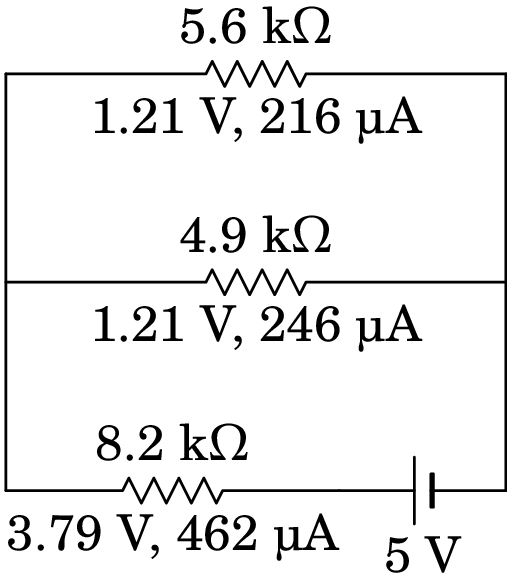
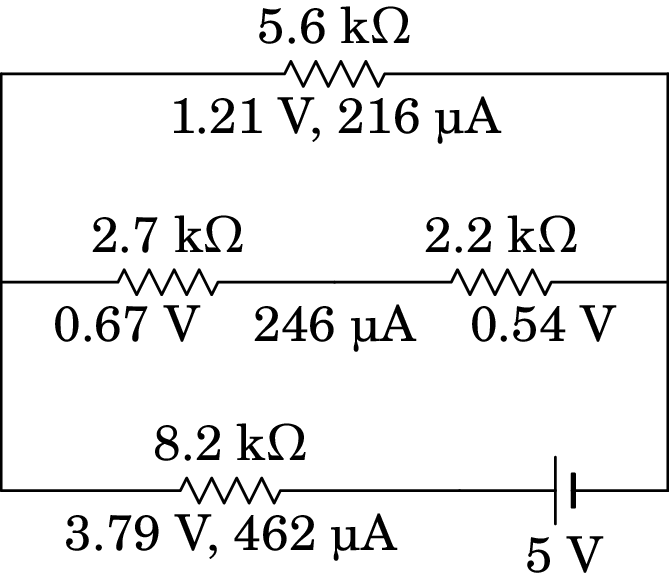
Finalmente, substitui-se a resistência de 4.9 k$\mathrm{\Omega }$ pelas resistências de 2.7 k$\mathrm{\Omega }$ e 2.2 k$\mathrm{\Omega }$, recuperando-se o circuito original. Nessas duas resistências em série a corrente de 246 µA será a mesma, e as diferenças de potencial obtêm-se multiplicando essa corrente pelos valores das duas resistências. A figura seguinte mostra a diferença de potencial e a corrente em todas as resistências do circuito original.

Problema 5.7

A temperatura num dado momento é 12 °C. Quanto deve aumentar a temperatura para que a resistência de um fio de cobre aumente 10%?

Resolução. Se $R_{12}$ for a resistência a 12 °C, a resistência à temperatura $T$ procurada será $R=1.1R_{12}$ ($R_{12}$ mais 10% de $R_{12}$). Estas duas resistências podem ser relacionadas com a resistência $R_{20}$, a 20 °C, através do valor do coeficiente de temperatura do cobre a 20 °C, $4.036\times {10}^{-3}$ ${}^{\circ }\mathrm{C}^{-1}$ (tabela 5.2 do livro de texto). Usando a equação (5.32) do livro de texto, temos então que:

$$\{\begin{array}{cc}{R}_{12}=R_{20}\left[1+4.036\times {10}^{-3}(12-20)\right]\hfill & \\ 1.1R_{12}=R_{20}\left[1+4.036\times {10}^{-3}(T-20)\right]\hfill & \end{array}$$

Dividindo a segunda equação pela primeira, eliminam-se $R_{12}$ e $R_{20}$ ficando uma equação com uma única variável, $T$:

$1.1={\displaystyle \frac{1+4.036\times {10}^3(T-20)}{0.9677}}$

$\iff \mathit{\hspace{1em}}T=20+{\displaystyle \frac{1.1\times 0.9677-1}{4.036\times {10}^3}}={36.0}^{\circ }\mathrm{C}$

Como tal, a temperatura deverá aumentar 24.0${}^{\circ }\mathrm{C}$ (de 12${}^{\circ }\mathrm{C}$ para 36.0${}^{\circ }\mathrm{C}$).

Problema 5.8

A resistência de uma lâmpada incandescente de 60 W e 230 V, cujo filamento é feito de tungsténio, medida à temperatura ambiente de 20 ${}^{\circ }\mathrm{C}$ é $R=65\mathrm{\Omega }$. No entanto, as especificações do fabricante (60 W e 230 V) conduzem a um valor muito mais elevado para a sua resistência. Justifique esta diferença, e calcule a temperatura do filamento de tungsténio quando a lâmpada se encontra acesa, assumindo que a resistividade elétrica do tungsténio varia linearmente com a temperatura.

Resolução. A potência e voltagem nominais, indicadas pelo fabricante, permitem determinar o valor da resistência nominal, usando a expressão da potência numa resistência, $P=\mathrm{\Delta }{V}^2/R$,

$$R=\frac{\mathrm{\Delta }{V}^2}{P}=\frac{{230}^2}{60}=881.7\mathrm{\Omega }$$

Esta é a resistência do filamento de tungsténio com a lâmpada acesa quando esta for ligada à voltagem de 230 V. O filamento, devido à sua temperatura elevada, emite radiação na região do visível (luz) e portanto a lâmpada ilumina.

A resistência a 20${}^{\circ }\mathrm{C}$, $R_{20}=65\mathrm{\Omega }$, quando a lâmpada está apagada, é muito menor e a esta temperatura o filamento de tungsténio não aquece o suficiente para poder iluminar. A temperatura do filamento de tungsténio com a lâmpada acesa obtém-se a partir da relação entre a resistência e a temperatura, usando o coeficiente de temperatura do tungsténio a 20 °C, o qual é igual a $4.484\times {10}^{-3}$ °C${}^{-1}$:

$$881.7=65\left[1+4.484\times {10}^{-3}(T-20)\right]\mathit{\hspace{1em}}\to \mathit{\hspace{1em}}T={2822}^{\circ }\mathrm{C}$$

Quando a diferença de potencial na lâmpada for de 230 V, o filamento aquecerá até 2822 ${}^{\circ }\mathrm{C}$, produzindo luz.

Comentários: O resultado anterior é apenas uma aproximação, já que a relação entre resistência e temperatura provavelmente já não será linear à temperatura elevada da lâmpada. De qualquer forma, a temperatura deve ser da ordem dos milhares de graus Celsius para que o filamento produza luz visível. A lâmpada não queima porque dentro dela não há oxigénio. O mecanismo de produção de luz usado nas lâmpadas incandescentes (aquecer um filamento) é muito ineficiente, pois grande parte da energia elétrica é dissipada sob a forma de calor; as lâmpadas fluorescentes são muito mais eficientes. Hoje em dia as lâmpadas de LEDs são ainda mais eficientes, aproveitando quase toda a energia elétrica para produzir luz.