7. Força magnética

Problema 7.1

Um protão (massa $1.673\times {10}^{-27}$ kg) encontra-se na origem, em $t=0$, com velocidade $\overrightarrow{v}=184\hat{ı}$ (km/s), dentro de uma região onde há vácuo e campo magnético uniforme: $\overrightarrow{B}=-0.062\hat{ȷ}$ (T). Determine a posição do protão em $t=0.85$ µs.

Resolução. Em $t=0$, a força magnética sobre o protão é (unidades SI):

$${\overrightarrow{F}}_0=1.602\times {10}^{-19}\left[184\times {10}^3\hat{ı}\times (-0.062\hat{ȷ})\right]=-1.8276\times {10}^{-15}\hat{k}$$

Observe-se que o peso do protão, $1.637\times {10}^{-26}$ N, é 11 ordens de grandeza inferior e, como tal, pode ser ignorado e não é necessário saber a direção da vertical.

Em $t=0$, o protão será desviado na direção negativa do eixo dos $z$; mais tarde, a força terá outra direção diferente, mas sempre no plano $xz$ (plano perpendicular a $\overrightarrow{B}$). Como tal, a trajetória do protão estará no plano $xz$. Como a força magnética é sempre perpendicular à velocidade, o módulo desta não muda e o módulo da força normal (magnética) permanece constante. O resultado é um movimento circular uniforme, no plano $xz$, com centro no semieixo negativo dos $z$, tal como mostra a figura seguinte.

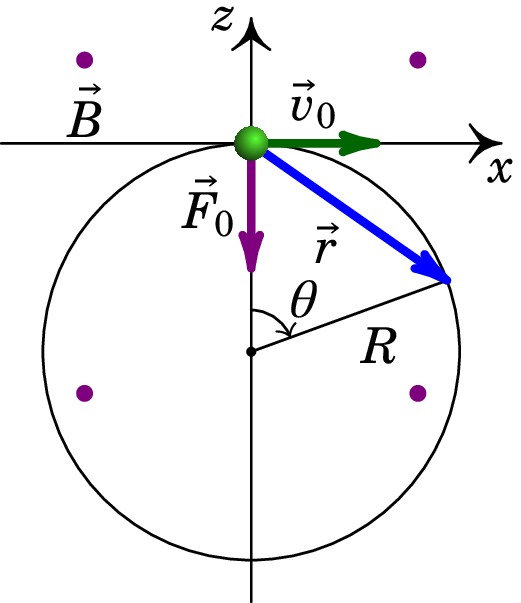
Basta uma variável para descrever a posição do protão, que pode ser o ângulo $\theta (t)$ indicado na figura, com $\theta =0$ em $t=0$. O vetor posição em qualquer instante $t\ge 0$ é:

$$\overrightarrow{r}(\theta )=R\left(\sin \theta \hat{ı}+\cos \theta \hat{k}\right)-R\hat{k}$$

O raio da trajetória determina-se igualando o módulo da força magnética à massa vezes a aceleração normal:

$1.8276\times {10}^{-15}=1.673\times {10}^{-27}\left({\displaystyle \frac{{184000}^2}{R}}\right)$

$R={\displaystyle \frac{5.654\times {10}^{-17}}{1.8276\times {10}^{-15}}}=0.03094\mathrm{m}$

E a velocidade angular (constante) é igual a,

$$\omega =\frac{v}{R}=\frac{184000}{0.03094}=5.947\times {10}^6{\mathrm{s}}^{-1}$$

Como a velocidade angular é constante e $\theta =0$ em $t=0$, a expressão do ângulo em função do tempo é:

$$\theta (t)=\omega t=5.947\times {10}^{6}t$$

e substituindo $t=0.85$ µs obtém-se o ângulo nesse instante (em radianos):

$$\theta =5.055$$

Finalmente, o vetor posição encontra-se substituindo $R$ e $\theta$ na expressão de $\overrightarrow{r}(\theta )$:

$$\overrightarrow{r}=\left(-2.91\hat{ı}-2.06\hat{k}\right)\mathrm{cm}$$

Problema 7.2

Um protão "navega"na atmosfera solar, a uma velocidade de $0.15c$, onde $c$ é a velocidade da luz no vazio ($2.998\times {10}^8$ m/s). O protão atravessa um campo magnético uniforme de 0.12 T, formando um ângulo de 25° com a sua velocidade. Calcule o raio do cilindro que envolve a órbita helicoidal do protão (a massa de um protão é $1.673\times {10}^{-27}$ kg e admita que com a velocidade $0.15c$ os efeitos relativistas são desprezáveis).

Resolução. A componente da velocidade no plano perpendicular ao plano é (unidades SI):

$$v_{⟂}=0.15\times 2.998\times {10}^8\sin {25}^{\circ }=1.901\times {10}^7$$

A projeção do movimento no plano perpendicular ao campo é movimento circular uniforme com raio igual a:

$$r=\frac{m{v}_{⟂}}{eB}=\frac{1.673\times {10}^{-27}\times 1.901}{1.602\times {10}^{-19}\times 0.12}=1.65\mathrm{m}$$

Problema 7.3

Um protão desloca-se no vácuo, com velocidade de $1.0\times {10}^6$ m/s, entrando numa região retangular onde existe campo magnético constante $\overrightarrow{B}$, perpendicular à sua velocidade, como mostra a figura. No ponto onde o protão penetra o campo magnético, a sua velocidade faz um ângulo de 28° com a fronteira do retângulo. Após a trajetória circular dentro do campo magnético, o protão sai do retângulo com velocidade que faz novamente um ângulo de 28° com a fronteira do retângulo. Sabendo que o módulo do campo magnético é 0.64 T, e a massa do protão é $1.673\times {10}^{-27}$ kg, determine a distância $d$ entre os pontos onde o protão entra e sai do retângulo onde existe campo magnético.

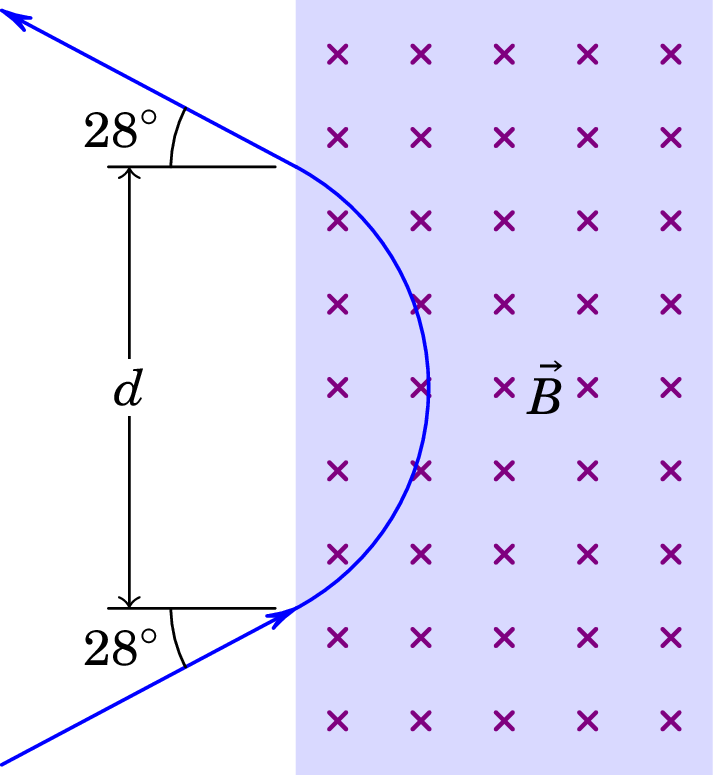
Resolução. Dentro do retângulo com campo magnético constante o movimento é circular uniforme com raio:

$$R=\frac{mv}{|q|B}$$

Nos pontos onde o protão entra e sai dessa região (A e B na figura seguinte), a velocidade é tangente ao arco de círculo dentro do retângulo. Como tal, o triângulo ABC, onde C é o centro do arco, tem dois lados de comprimento $R$ e dois ângulos de ${28}^{\circ }$:

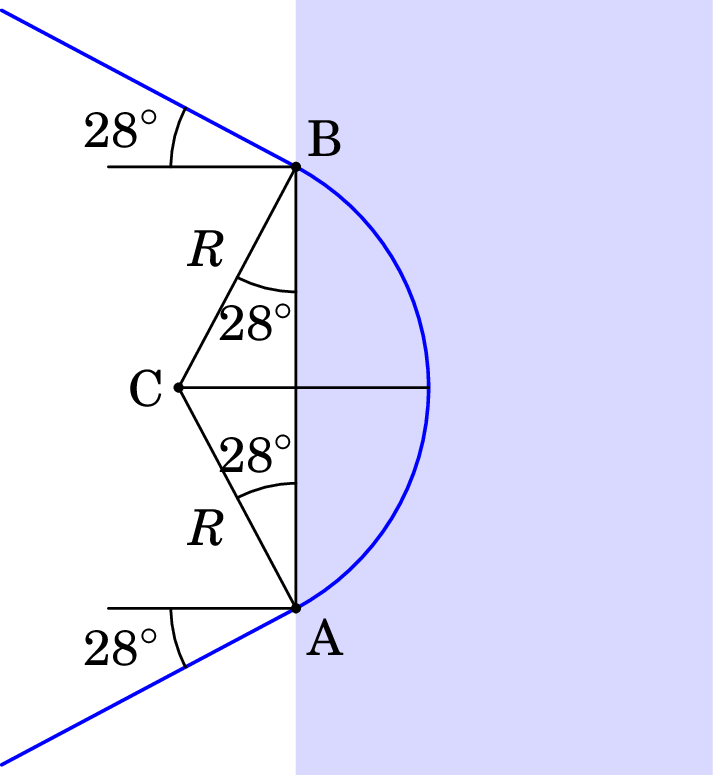
A partir da figura conclui-se que:

$d$ $=\overline{AB}=2R\cos {28}^{\circ }={\displaystyle \frac{2mv\cos {28}^{\circ }}{|q|B}}$

$={\displaystyle \frac{2\times 1.673\times {10}^{-27}\times {10}^6\times 0.8829}{1.602\times {10}^{-19}\times 0.64}}=28.85\mathrm{mm}$

Problema 7.4

Uma partícula com carga de $2.5$ nC encontra-se numa região onde existe campo magnético uniforme $\overrightarrow{B}$. Quando se move com velocidade ${\overrightarrow{v}}_1$, no plano $yz$ e fazendo um ângulo $\theta ={10}^{\circ }$ com o eixo dos $y$, tal como mostra a figura, a força magnética sobre ela é ${\overrightarrow{F}}_1$, na direção e sentido do eixo dos $x$. Quando a velocidade da partícula é ${\overrightarrow{v}}_2=\left(2.5\times {10}^4\hat{ı}+3.2\times {10}^4\hat{ȷ}\right)$ m/s, a força magnética sobre ela é ${\overrightarrow{F}}_2=\left(32\hat{ı}-25\hat{ȷ}+37.5\hat{k}\right)$ µN. Determine o campo $\overrightarrow{B}$.

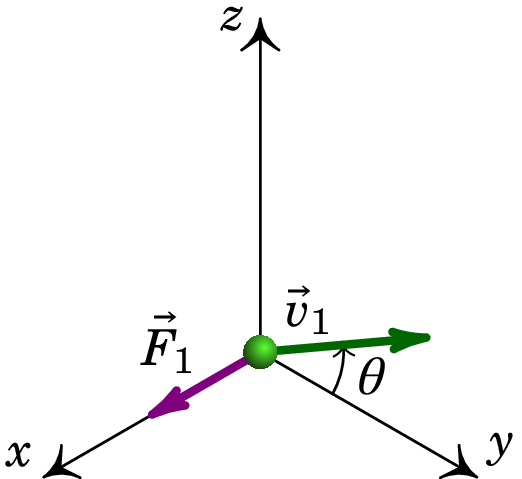
Resolução. Como o campo magnético deve ser perpendicular a ${\overrightarrow{F}}_1$, a sua componente $x$ será nula e terá a forma geral:

$$\overrightarrow{B}=B_y\hat{ȷ}+B_z\hat{k}$$

Quando a velocidade da partícula for ${\overrightarrow{v}}_2$, a força magnética sobre a partícula será igual à carga vezes o produto vetorial entre ${\overrightarrow{v}}_2$ e $\overrightarrow{B}$ que dá

${\overrightarrow{F}}_2$ $=2.5\times {10}^{-9}\left(2.5\times {10}^4\hat{ı}+3.2\times {10}^4\hat{ȷ}\right)\times \left(B_y\hat{ȷ}+B_z\hat{k}\right)$

$=\left(80B_z\hat{ı}-62.5B_z\hat{ȷ}+62.5B_y\hat{k}\right)\times {10}^{-6}$

Igualando as três componentes desse vetor às 3 componentes dadas de ${\overrightarrow{F}}_2$, obtém-se um sistema de três equações,

que conduz às componentes do campo magnético:

$$\overrightarrow{B}=\left(0.6\hat{ȷ}+0.4\hat{k}\right)\mathrm{T}$$

Problema 7.5

A espira triangular na figura tem um vértice na origem, o vértice P no eixo dos $z$, a 30 cm da origem, e o vértice Q no eixo dos $y$, a 40 cm da origem. Existe um campo magnético uniforme $\overrightarrow{B}=0.05\hat{ı}+0.03\hat{ȷ}-0.08\hat{k}$ (em teslas) e na espira circula corrente de intensidade $I=23.4$ mA, no sentido indicado na figura.
(a) Determine a força magnética sobre cada um dos três lados da espira.
(b) Determine a força magnética total sobre a espira.
(c) Determine o momento do binário magnético sobre a bobina.

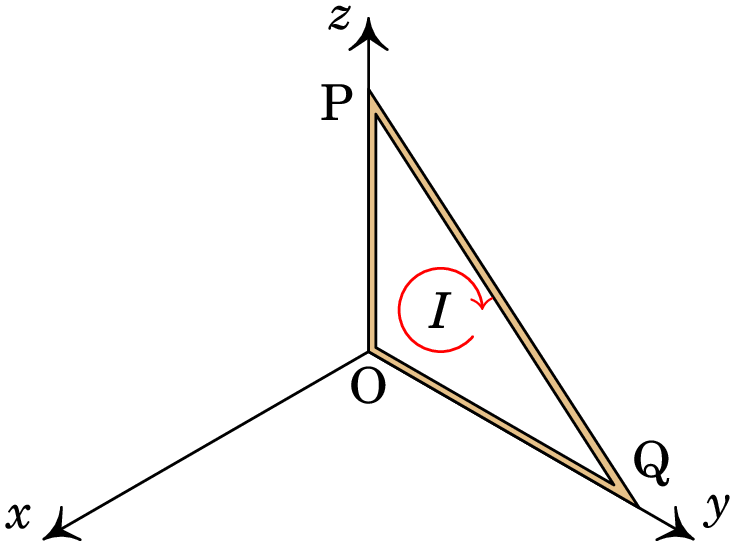
Resolução. (b) É conveniente começar por resolver a alínea b, que ajudará no cálculo da alínea a. Como o campo magnético é constante, a expressão da força magnética sobre o fio retilíneo entre os pontos P e Q é

$${\overrightarrow{F}}_{\mathrm{PQ}}=\overline{\mathrm{PQ}}\left(\overrightarrow{I}\times \overrightarrow{B}\right)=I\left(\overrightarrow{\mathrm{PQ}}\times \overrightarrow{B}\right)$$

Onde $\overline{\mathrm{PQ}}$ é a distância entre os pontos P e Q e $\overrightarrow{\mathrm{PQ}}$ é o vetor com origem em P e fim em Q. Como tal, a força total sobre a espira é:

$$\overrightarrow{F}=I\left(\overrightarrow{\mathrm{PQ}}\times \overrightarrow{B}\right)+I\left(\overrightarrow{\mathrm{QO}}\times \overrightarrow{B}\right)+I\left(\overrightarrow{\mathrm{OP}}\times \overrightarrow{B}\right)=I\left(\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{QO}}+\overrightarrow{\mathrm{OP}}\right)\times \overrightarrow{B}=\overrightarrow{0}$$

já que a soma dos três vetores entre os parêntesis é igual a zero.

(a) Usando unidades de mA para a corrente, mm para as distâncias e T para o campo, as forças calculadas estarão todas em µN. A força sobre o segmento entre O e P é:

$${\overrightarrow{F}}_{\mathrm{OP}}=23.4\left(300\hat{k}\right)\times \left(0.05\hat{ı}+0.03\hat{ȷ}-0.08\hat{k}\right)=-210.6\hat{ı}+351\hat{ȷ}$$

No segmento entre Q e O é:

$${\overrightarrow{F}}_{\mathrm{QO}}=23.4\left(-400\hat{ȷ}\right)\times \left(0.05\hat{ı}+0.03\hat{ȷ}-0.08\hat{k}\right)=748.8\hat{ı}+468\hat{k}$$

E como a soma das três forças é nula, a força sobre o segmento entre P e Q é (em µN):

$${\overrightarrow{F}}_{\mathrm{PQ}}=-{\overrightarrow{F}}_{\mathrm{OP}}-{\overrightarrow{F}}_{\mathrm{QO}}=-538.2\hat{ı}-351\hat{ȷ}-468\hat{k}$$

(c) O versor normal à espira, no sentido da regra da mão direita segundo a corrente, é o versor $-\hat{ı}$ e o momento magnético da espira, em unidades SI, é igual a:

$$\overrightarrow{m}=-\left(\frac{0.3\times 0.4}{2}\right)23.4\times {10}^{-3}\hat{ı}=-1.404\times {10}^{-3}\hat{ı}$$

O momento do binário magnético é:

$\overrightarrow{M}$ $=-1.404\times {10}^{-3}\hat{ı}\times \left(0.05\hat{ı}+0.03\hat{ȷ}-0.08\hat{k}\right)$

$=-\left(112.32\hat{ȷ}+42.12\hat{k}\right)\times {10}^{-6}\mathrm{N}\cdot \mathrm{m}$

Problema 7.6

Num filtro de velocidades há campos elétrico e magnético uniformes e perpendiculares, e as partículas entram com velocidade perpendicular aos dois campos. O módulo do campo magnético é 0.1 T e o do campo elétrico 0.2 MV/m.
(a) Qual a velocidade das partículas à saída do filtro? (partículas que não são desviadas na sua passagem pelo filtro.)
(b) Qual a energia dum protão à saída do filtro?
(c) Qual a energia de um eletrão à saída do filtro?

Resolução. (a) A velocidade das partículas que atravessam o filtro é igual à relação entre os módulos dos campos elétrico e magnético:

$$v=\frac{0.2\times {10}^6}{0.1}=2\times {10}^6\frac{\mathrm{m}}{\mathrm{s}}$$

(b) Como a velocidade das partículas é muito menor do que a velocidade da luz, usa-se a expressão não relativista para determinar a energia cinética dum protão:

$$E=\frac{1}{2}1.673\times {10}^{-27}{\left(2\times {10}^6\right)}^2=3.35\times {10}^{-15}\mathrm{J}$$

(c) No caso dum eletrão, a energia cinética é igual a:

$$E=\frac{1}{2}9.109\times {10}^{-31}{\left(2\times {10}^6\right)}^2=1.82\times {10}^{-18}\mathrm{J}$$

Problema 7.7

Calcule a intensidade máxima do momento do binário magnético que atua sobre uma bobina circular de 400 espiras de raio 0.1 cm, percorrida por uma corrente de 92 mA, num campo magnético uniforme de 0.3 T.

Resolução. O módulo do momento magnético da bobina é igual a (unidades SI):

$$m=400\times \pi {0.001}^2\times 92\times {10}^{-3}=1.156\times {10}^{-4}$$

E o momento do binário magnético máximo é igual ao produto do módulo do momento magnético vezes o módulo do campo magnético:

$$M_{\text{máx}}=1.156\times {10}^{-4}\times 0.3=3.47\times {10}^{-5}\mathrm{N}\cdot \mathrm{m}$$

Problema 7.8

Um feixe de protões desloca-se com velocidade constante $\overrightarrow{v}$, segundo o eixo dos $x$, atravessando duas regiões, I e II, caraterizadas do seguinte modo: em I, existe um campo magnético, ${\overrightarrow{B}}_1$ e em II, coexistem um campo magnético, ${\overrightarrow{B}}_2$, e um campo elétrico, $\overrightarrow{E}=E\hat{ȷ}$. Todos os campos são uniformes nas regiões em que foram definidos e anulam-se fora delas. O peso dos protões não é significativo. Quais as condições a que devem obedecer os campos ${\overrightarrow{B}}_1$ e ${\overrightarrow{B}}_2$ para que o feixe não sofra qualquer perturbação no seu movimento, enquanto atravessa duas regiões? Se em vez de protões, fosse um feixe de eletrões, as condições estabelecidas manter-se-iam?

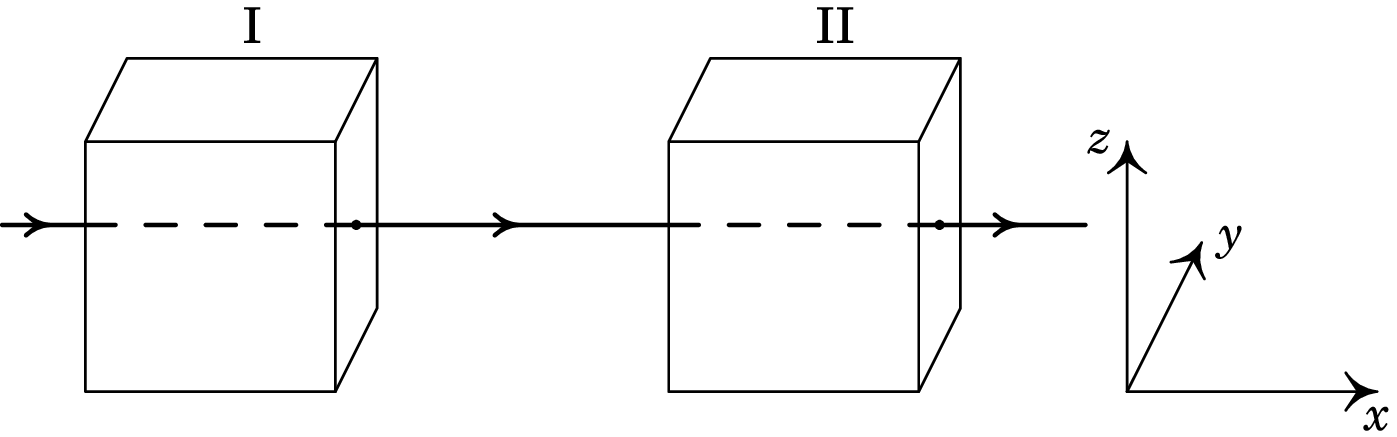
Resolução. A velocidade de cada protão é igual a,

$$\overrightarrow{v}=v\hat{ı}$$

Na região I, a força magnética que atua sobre cada protão é,

${\overrightarrow{F}}_1$ $=q\overrightarrow{v}\times {\overrightarrow{B}}_1=qv\hat{ı}\times \left(B_x\hat{ı}+B_y\hat{ȷ}+B_z\hat{k}\right)$

$=qv\left(B_y\hat{k}-B_z\hat{ȷ}\right)$

Para que o feixe não seja desviado, a duas componentes $\hat{ȷ}$ e $\hat{k}$ da força devem ser nulas, ou seja, $B_y=B_z=0$. O campo na região I tem então a forma geral ${\overrightarrow{B}}_1=B_1\hat{ı}$, onde $B_1$ pode ter qualquer valor, positivo ou negativo. Como tal, basta com que o campo magnético na região I seja na mesma direção da velocidade dos protões para que estes não sejam desviados.

Na região II é necessário acrescentar a força elétrica:

$${\overrightarrow{F}}_2=q\overrightarrow{E}+q\overrightarrow{v}\times {\overrightarrow{B}}_2=q\left(E\hat{ȷ}+v{B}_y\hat{k}-v{B}_z\hat{ȷ}\right)$$

Para que a componente $\hat{k}$ seja nula, é necessário $B_y=0$, e para que a componente $\hat{ȷ}$ seja nula, é necessário $E=v{B}_z$. Como tal, a forma geral do campo magnético na região II é a seguinte

$${\overrightarrow{B}}_2=B_x\hat{ı}+\frac{E}{v}\hat{k}$$

onde $B_x$ pode ter qualquer valor, positivo ou negativo. Ou seja, o campo magnético na região II deverá ter uma componente perpendicular à velocidade e ao campo elétrico, com módulo igual ao módulo do campo elétrico dividido pela velocidade, e pode ter também uma componente paralela à velocidade.

Se o feixe fosse composto por eletrões, ou qualquer outro tipo de partículas com carga, as condições obtidas seriam as mesmas, já que os resultados não dependem do valor de $q$ nem da massa das partículas.

Comentários: Observe-se que na região II o campo magnético necessário para que as partículas não sejam desviadas depende da velocidade $v$ das partículas. Como tal, na região II há um filtro de velocidades, em que as partículas com velocidade $v=B_z/E$ passam sem serem desviadas, mas as partículas com velocidades diferentes desse valor serão desviadas.