9. Indução eletromagnética

Problema 9.1

O comprimento total entre as pontas das asas de um avião Boeing 747 é 60 m . O avião voa a 800 km/h e com altura constante, na direção sul-norte, numa região onde o campo magnético terrestre faz um ângulo de 60${}^{\circ }$ com a vertical e a sua intensidade é 0.5 G. Calcule a diferença de potencial induzida entre as pontas da asas.

Resolução. Escolhendo o eixo $x$ na direção de oeste para leste, o eixo $y$ na direção de sul para norte e o eixo $z$ na vertical, de baixo para cima, a velocidade do avião e o campo magnético são (unidades SI):

$$\overrightarrow{v}=\frac{800}{3.6}\hat{ȷ}\mathit{\hspace{1em}\hspace{1em}}\overrightarrow{B}=5\times {10}^{-5}\left(\frac{\sqrt{3}}{2}\hat{ȷ}+\frac{\hat{k}}{2}\right)$$

O campo elétrico induzido é igual a

$${\overrightarrow{E}}_{\mathrm{i}}=\overrightarrow{v}\times \overrightarrow{B}=\frac{800\times 5\times {10}^{-5}}{3.6}\hat{ȷ}\times \left(\frac{\sqrt{3}}{2}\hat{ȷ}+\frac{\hat{k}}{2}\right)=5.556\times {10}^{-3}\hat{ı}$$

O deslocamento infinitesimal ao longo das assas do avião é:

$$\mathrm{d}\overrightarrow{r}=\hat{ı}\mathrm{d}x$$

E a f.e.m. induzida nas assas é o integral de linha do campo elétrico induzido, ao longo das assas:

$${\epsilon }_{\mathrm{i}}=\int {\overrightarrow{E}}_{\mathrm{i}}\cdot d\overrightarrow{r}={\int }_0^{60}5.556\times {10}^{-3}\left(\hat{ı}\cdot \hat{ı}\right)dx=5.556\times {10}^{-3}{\int }_0^{60}dx=0.333\mathrm{V}$$

Problema 9.2

A figura mostra uma barra condutora de comprimento $d$ e massa $m$ que desliza sobre dois trilhos metálicos verticais, dentro de um campo magnético $\overrightarrow{B}$ uniforme. A resistência elétrica dos trilhos e da barra são desprezáveis comparadas com $R$. A barra mantém sempre o contato com os trilhos, permitindo que circule corrente pela resistência $R$, mas o atrito é desprezável, assim como o efeito da resistência do ar na barra. Quando a barra começa a cair livremente, o seu movimento é inicialmente acelerado mas rapidamente atinge uma velocidade constante $v$. Calcule o valor dessa velocidade limite $v$.

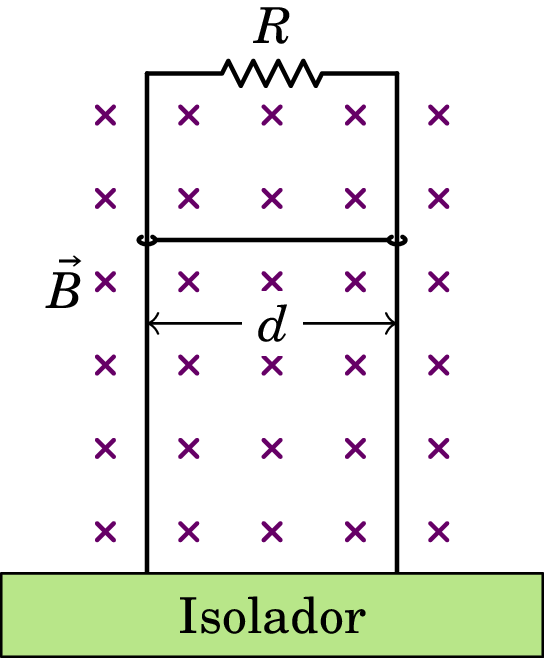
Resolução. Quando a barra já desceu uma distância $y$ em relação à resistência $R$, a área da espira retangular formada pela barra, os trilhos e a resistência é $A=yd$ e o fluxo magnético através dela é $\mathrm{\Phi }=Byd$.

A f.e.m. e a corrente induzidas na espira são:

$${\epsilon }_{\mathrm{i}}=-Bd\frac{\mathrm{d}y}{\mathrm{d}t}=-Bvd\mathit{\hspace{1em}\hspace{1em}}{I}_{\mathrm{i}}=\frac{|{\epsilon }_{\mathrm{i}}|}{R}=\frac{Bvd}{R}$$

A variação do fluxo aponta para dentro da folha e, pela lei de Lenz, a corrente induzida passa pela barra de esquerda para direita, dando origem a força magnética para cima, com módulo:

$$F_{\mathrm{m}}=I_{\mathrm{i}}Bd=\frac{B^{2}v{d}^2}{R}$$

Inicialmente (no repouso) essa força é nula e a barra desce com a aceleração da gravidade. Enquanto a velocidade $v$ aumenta, a força magnética também aumenta, fazendo diminuir a força resultante. No instante em que a força resultante é nula, a velocidade atinge o valor limite e os módulos da força magnética e do peso são iguais:

$$mg=\frac{B^{2}v{d}^2}{R}\mathit{\hspace{1em}\hspace{1em}}⟹\mathit{\hspace{1em}\hspace{1em}}v=\frac{mgR}{B^2{d}^2}$$

Problema 9.3

Uma bobina retangular com 400 espiras, todas com arestas de 1.5 cm e 3 cm, é atravessada por um campo magnético externo $\overrightarrow{B}$ de módulo 0.2 T, perpendicular aos planos das espiras. A resistência total da bobina é 42 $\mathrm{\Omega }$. Ligam-se entre si os dois extremos, inicial e final, da bobina e o campo externo é reduzido até 0, durante um intervalo de 4 segundos. Determine a carga total transferida através da bobina durante esse intervalo.

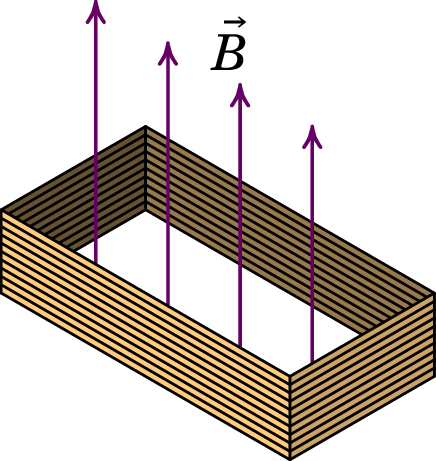
Resolução. O fluxo magnético inicial, através da bobina, é igual a

$${\mathrm{\Phi }}_0=NBA$$

onde $N$ é o número de espiras, $B$ o módulo do campo magnético e $A$ a área de cada espira. O fluxo final ${\mathrm{\Psi }}_f$ é nulo e a f.e.m. induzida média é:

$${\overline{\epsilon }}_{\mathrm{i}}=-\frac{\mathrm{\Delta }\mathrm{\Phi }}{\mathrm{\Delta }t}=\frac{NBA}{\mathrm{\Delta }t}$$

A corrente média é:

$$\overline{I}=\frac{{\overline{\epsilon }}_{\mathrm{i}}}{R}=\frac{NBA}{R\mathrm{\Delta }t}$$

E a carga transferida é igual a:

$$\mathrm{\Delta }Q=\overline{I}\mathrm{\Delta }t=\frac{NBA}{R}$$

Substituindo os valores dados obtém-se:

$$\mathrm{\Delta }Q=\frac{400\times 0.2\times 0.015\times 0.03}{42}=8.57\times {10}^{-4}\mathrm{C}=0.857\mathrm{mC}$$

Problema 9.4

A bobina cilíndrica na figura tem 23 espiras de raio 1.6 cm. O eixo da bobina coincide com o eixo dos $x$, em $t=0$, mas em $t>0$ roda no plano $xy$ com velocidade angular constante $\omega =40{\mathrm{s}}^{-1}$, no sentido indicado na figura. Na região onde a bobina roda existe campo magnético variável:

$$\overrightarrow{B}=2.2{\mathrm{e}}^{-14t}\hat{ȷ}\mathit{\hspace{1em}\hspace{1em}}\text{(unidades SI)}$$

Determine a expressão da f.e.m. induzida na bobina, em função do tempo $t$, para $t>0$.

Resolução. A velocidade angular é igual à derivada do ângulo entre o eixo da bobina e o eixo dos $x$: $\mathrm{d}\theta /\mathrm{d}t=\omega =40$. Como esse ângulo é igual a zero no instante $t=0$, a expressão do ângulo em função do tempo é (unidades SI):

$$\theta =40t$$

e a expressão do versor normal à bobina, em função do tempo, é:

$$\hat{n}=\cos (40t)\hat{ı}+\sin (40t)\hat{ȷ}$$

O fluxo magnético através da bobina é a soma dos fluxos em todas as espiras (unidades SI):

$\mathrm{\Phi }$ $=N{\displaystyle {\iint }_{\text{espira}}}\overrightarrow{B}\cdot d\overrightarrow{A}=\pi N{r}^2\left(\overrightarrow{B}\cdot \hat{n}\right)$

$=23\pi {(0.016)}^2\left(2.2{\mathrm{e}}^{-14t}\right)\sin (40t)=0.04069{\mathrm{e}}^{-14t}\sin (40t)$

A f.e.m. induzida é igual a menos a derivada do fluxo magnético em ordem ao tempo:

$$\epsilon =-\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}={\mathrm{e}}^{-14t}\left[0.5697\sin (40t)-1.628\cos (40t)\right]$$

Problema 9.5

A espira retangular na figura tem arestas $a=30$ cm e $b=63$ cm. No mesmo plano da espira encontra-se um fio condutor retilíneo e muito comprido, paralelo a uma das arestas de lado $b$ e a uma distância $d=34$ cm dela. Determine a expressão da f.e.m. induzida na espira, em função do tempo $t$, quando o fio retilíneo é percorrido por corrente com intensidade $I=0.42\sin (168t)$ (unidades SI).

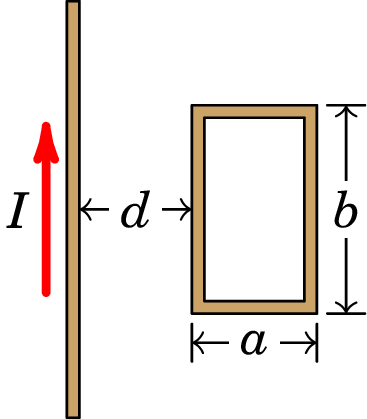
Resolução O campo magnético que o fio produz através da espira é perpendicular à espira e com módulo (SI):

$$B=\frac{2k_{\mathrm{m}}I}{\varrho }=\frac{0.84\times {10}^{-7}\sin (168t)}{\varrho }$$

onde $\varrho$ é a distância desde o fio, que varia entre $d$ e $d+a$ na espira.

O fluxo magnético na espira é o integral de superfície, na espira, da componente perpendicular do campo magnético:

$\mathrm{\Phi }$ $={\displaystyle {\int }_0^{0.63}}{\displaystyle {\int }_{0.34}^{0.64}}Bd\varrho dy$

$=0.63\times 0.84\times {10}^{-7}\sin (168t)\left[\ln (0.64)-\ln (0.34)\right]$

$=33.473\times {10}^{-9}\sin (168t)$

E a f.e.m. induzida é igual a menos a derivada desse fluxo, em ordem ao tempo:

$$\epsilon =-\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}=-5.62\times {10}^{-6}\cos (168t)$$

Problema 9.6

Uma espira condutora retangular, paralela ao plano O$yz$, desloca-se com velocidade constante $\overrightarrow{v}=3\hat{ȷ}$ (m/s) dentro de uma região onde existe um campo magnético com componentes: $B_x=(6-y)$ (SI) e $B_y=B_z=0$. Calcule a f.e.m. induzida na espira, em função do tempo $t$, a partir do instante $t=0$ em que a espira se encontra na posição da figura, com um lado ao longo do eixo dos $z$.

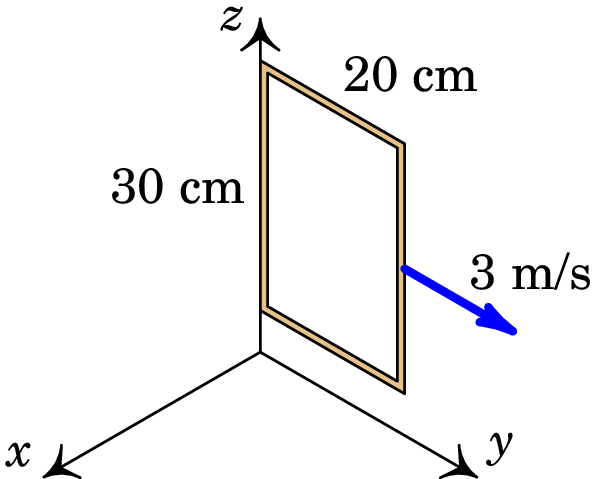
Resolução. A componente do campo perpendicular à espira é (unidades SI):

$$\overrightarrow{B}\cdot \hat{n}=\overrightarrow{B}\cdot \hat{ı}=B_x=6-y$$

A aresta que se encontra no eixo dos $z$ em $t=0$, estará na posição $3t$ num instante $t$, e a outra aresta, paralela ao eixo dos $z$, estará em $3t+0.2$. As duas arestas paralelas ao eixo dos $y$ estão sempre nas posições $z_0$ e $z_0+0.3$.

O fluxo magnético através da espira é então:

$$\mathrm{\Phi }={\int }_{3t}^{3t+0.2}{\int }_{z_0}^{z_0+0.3}(6-y)dzdy=0.354-0.18t$$

E a f.e.m. induzida é igual a:

$${\epsilon }_{\mathrm{i}}=-\frac{\mathrm{d}\mathrm{\Phi }}{\mathrm{d}t}=0.18\mathrm{V}$$

O sinal positivo indica que é no sentido da regra da mão direita em relação ao versor $\hat{n}$ usado, ou seja, $\hat{ı}$. Como tal, a f.e.m. induzida produz corrente induzida no sentido da rotação do eixo dos $y$ para o eixo dos $z$.

Problema 9.7

No circuito da figura, calcule as correntes iniciais no indutor e no condensador, a corrente final no indutor e a carga final no condensador.

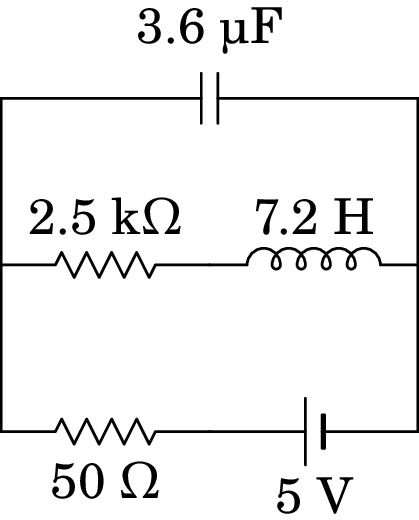
Resolução. Os circuitos equivalentes inicial e final são os seguintes:

No instante inicial, a corrente no indutor é nula e a corrente no condensador é:

$$I_0=\frac{5}{50}=0.1\mathrm{A}$$

No instante final, a corrente no indutor é:

$$I_{\mathrm{\infty }}=\frac{5}{50+2500}=1.961\mathrm{mA}$$

A diferença de potencial no condensador é:

$$\mathrm{\Delta }V=2500I_{\mathrm{\infty }}=4.902\mathrm{V}$$

e a carga nele é:

$$Q=3.6\times {10}^{-6}\times 4.902=17.65\mu \mathrm{C}$$

Problema 9.8

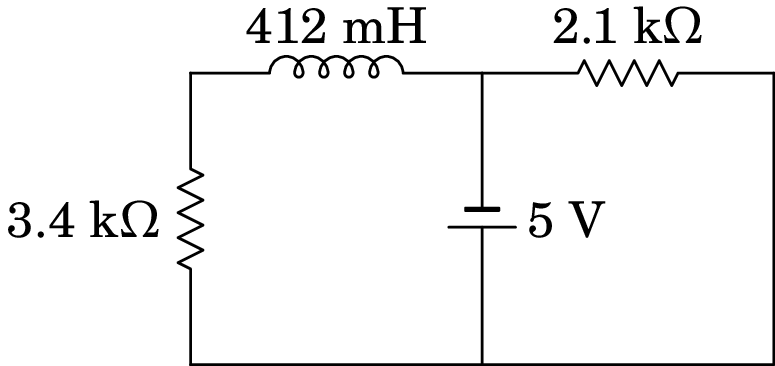
No circuito representado no diagrama, a fonte foi ligada no instante $t=0$, quando não havia corrente no indutor.
(a) Determine a voltagem na resistência de 3.4 k$\mathrm{\Omega }$ em $t=0$.
(b) Determine o valor da derivada da voltagem na resistência de 3.4 k$\mathrm{\Omega }$, em $t=0$.
(c) Determine a voltagem na resistência de 3.4 k$\mathrm{\Omega }$, quando o circuito atingir o estado estacionário.

Resolução. (a) O circuito equivalente em $t=0$ é o seguinte:

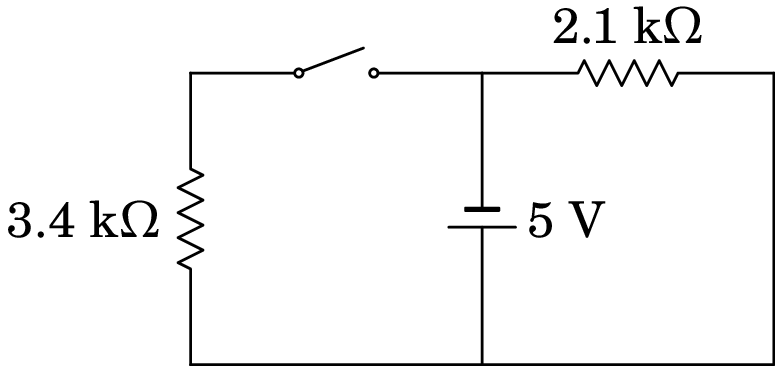
Como a corrente na resistência de 3.4 k$\mathrm{\Omega }$ é nula, a voltagem nela também é igual a zero.

(b) Se $V(t)$ e $I(t)$ são a voltagem e a intensidade da corrente na resistência de 3.4 k$\mathrm{\Omega }$, em função do tempo, a lei de Ohm implica (unidades SI):

$$\frac{\mathrm{d}V}{\mathrm{d}t}=3400\frac{\mathrm{d}I}{\mathrm{d}t}$$

E como em qualquer instante a corrente na resistência de 3.4 k$\mathrm{\Omega }$ é igual à corrente no indutor, usando a relação entre voltagem no indutor, $V_L$, e a corrente nele, obtém-se:

$$\frac{\mathrm{d}I}{\mathrm{d}t}=\frac{V_L}{L}=\frac{V_L}{0.412}$$

Em $t=0$, o circuito equivalente da alínea a mostra que a voltagem no indutor é $V_L=5$ V. Como tal, a derivada da voltagem na resistência, em $t=0$, é:

$${\frac{\mathrm{d}V}{\mathrm{d}t}|}_0=3400\left(\frac{5}{0.412}\right)=41.26\frac{\mathrm{kV}}{\mathrm{s}}$$

É positiva, porque a corrente no indutor, nula em $t=0$, está a aumentar e, portanto, a corrente e voltagem na resistência também estão a aumentar.

(c) O circuito equivalente em $t\to \mathrm{\infty }$ é o seguinte:

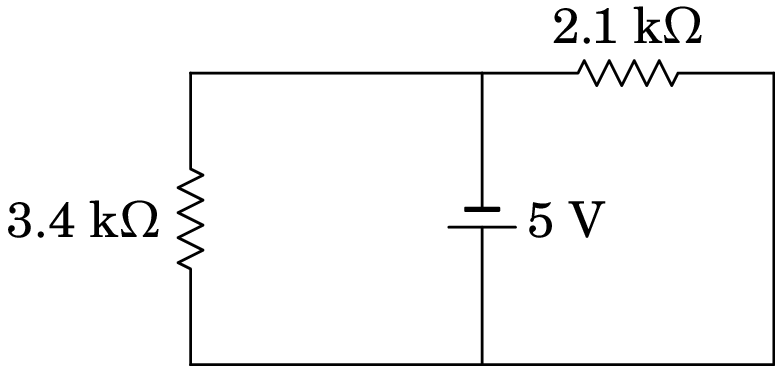
Ou seja, a voltagem na resistência de 3.4 k$\mathrm{\Omega }$ é igual a 5 V.