3. Potencial eletrostático

Jaime E. Villate e Luís Miguel Martelo

(15 de novembro de 2024)

Problema 3.1

Demonstre a identidade:

\vec{\nabla}\Bigl{(}\dfrac{1}{r}\Bigr{)}=-\dfrac{\vec{r}}{r^{3}}=-\dfrac{\hat{% r}}{r^{2}}

Resolução. Em coordenadas cartesianas,

r^{-1}=\bigl{(}x^{2}+y^{2}+z^{2}\bigr{)}^{-1/2}

e o gradiente é,

	$\displaystyle\vec{\nabla}\Bigl{(}\dfrac{1}{r}\Bigr{)}$	$\displaystyle=-\dfrac{2x\,\hat{\imath}}{2\bigl{(}x^{2}+y^{2}+z^{2}\bigr{)}^{3/% 2}}-\dfrac{2y\,\hat{\jmath}}{2\bigl{(}x^{2}+y^{2}+z^{2}\bigr{)}^{3/2}}-\dfrac{% 2z\,\hat{k}}{2\bigl{(}x^{2}+y^{2}+z^{2}\bigr{)}^{3/2}}$
		$\displaystyle=-\dfrac{\vec{r}}{r^{3}}=-\dfrac{\hat{r}}{r^{2}}$

Problema 3.2

Uma esfera metálica encontra-se próxima de outra peça metálica formada por um cilindro e duas semiesferas, como mostra a figura. Ambos objetos estão isolados de qualquer outro condutor. A esfera tem carga positiva ( $Q_{1}>0$ ) e a peça cilíndrica está completamente descarregada ( $Q_{2}=0$ ). Arbitrando que o potencial da peça cilíndrica é zero, então o potencial da esfera é 80 V. Faça um desenho mostrando as duas peças, a distribuição de cargas, as linhas de campo nas duas peças e à sua volta, e as superfícies equipotenciais de -5 V, 5 V e 75 V.

Resolução. Há que ter em conta várias coisas:

•

As cargas distribuem-se nas superfícies dos dois condutores. No cilindro são induzidas cargas negativas no extremo mais próximo da esfera e o mesmo número de cargas positivas no extremo mais afastado. Na superfície da esfera há cargas positivas, mais concentradas no extremo próximo do cilindro.
•

Não há linhas de campo dentro da esfera nem dentro do cilindro. Há linhas de campo a começar na superfície da esfera e na superfície do cilindro, no extremo onde há carga positiva, e linhas de campo a terminar na superfície do cilindro, no extremo onde há carga negativa.
•

Todas as linhas de campo são perpendiculares à superfície do objeto onde começam ou terminam.
•

Nenhuma linha de campo pode começar num extremo do cilindro e terminar no outro, porque o potencial é constante no cilindro, enquanto que o potencial onde começa uma linha é sempre maior do que o potencial onde esta termina.
•

A equipotencial de $75$ V estará próxima da esfera, onde o potencial é $80$ V, e as equipotenciais de $5$ V e $-5$ V estarão próximas do cilindro, onde o potencial é $0$ . No entanto, nenhuma dessas equipotenciais pode tocar nenhum dos objetos, porque estes têm valores de potencial diferentes de $75$ V, $5$ V e $-5$ V.
•

Essas 3 equipotenciais não se podem cruzar entre si, por terem valores de potencial diferentes, e devem ser perpendiculares às linhas de campo elétrico, em todos os pontos onde se cruzam com elas.

O gráfico é aproximadamente o seguinte:

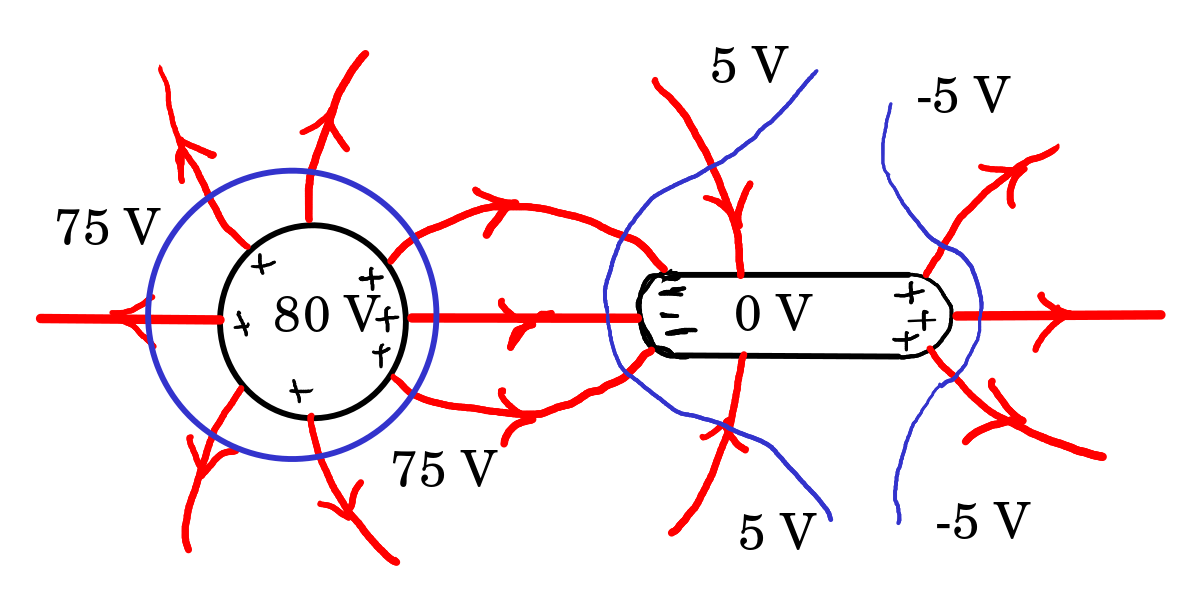
Também pode ser representado visto de longe:

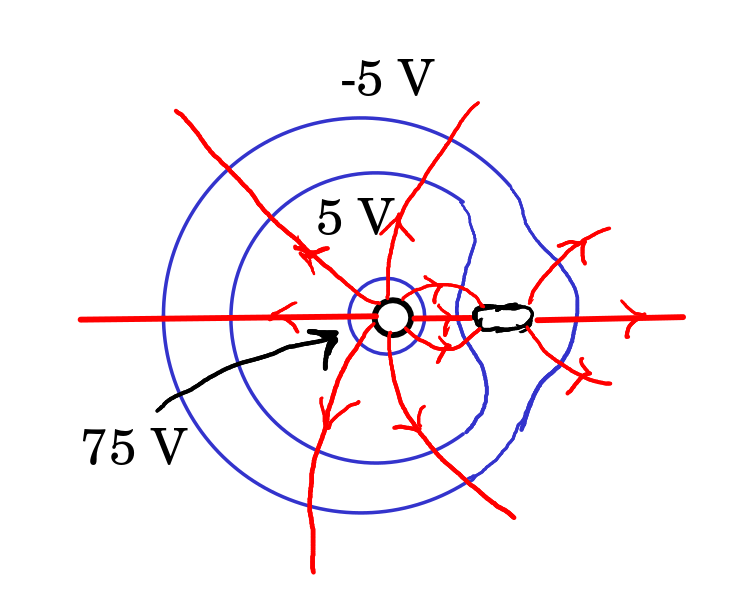
Problema 3.3

O potencial elétrico a uma certa distância de uma carga pontual é 600 V (arbitrando potencial nulo no infinito) e o valor do campo elétrico é 200 N/C. Calcule a distância e o valor da carga.

Resolução. Usando as expressões do potencial e do módulo do campo eléctrico de uma carga pontual, em unidades SI,

600=\dfrac{kq}{d}\qquad 200=\dfrac{kq}{d^{2}}

onde $d$ é a distância atá à carga. Dividindo uma equação pela outra temos:

d=3

e substituindo na equação do potencial,

kq=600\times 3\qquad\Longrightarrow\qquad q=2.00\times 10^{-7}

o valor da carga é 200 nC e encontra-se a 3 m.

Problema 3.4

A figura representa as linhas de campo eletrostático de duas partículas carregadas e separadas por uma distância de 7 cm. A razão entre os valores das duas cargas é 4/9.
(a) Calcule a distância do ponto P às partículas.
(b) Sabendo que a carga da partícula no lado direito é de $-8$ nC, calcule o potencial no ponto P (arbitre $V=0$ no infinito).

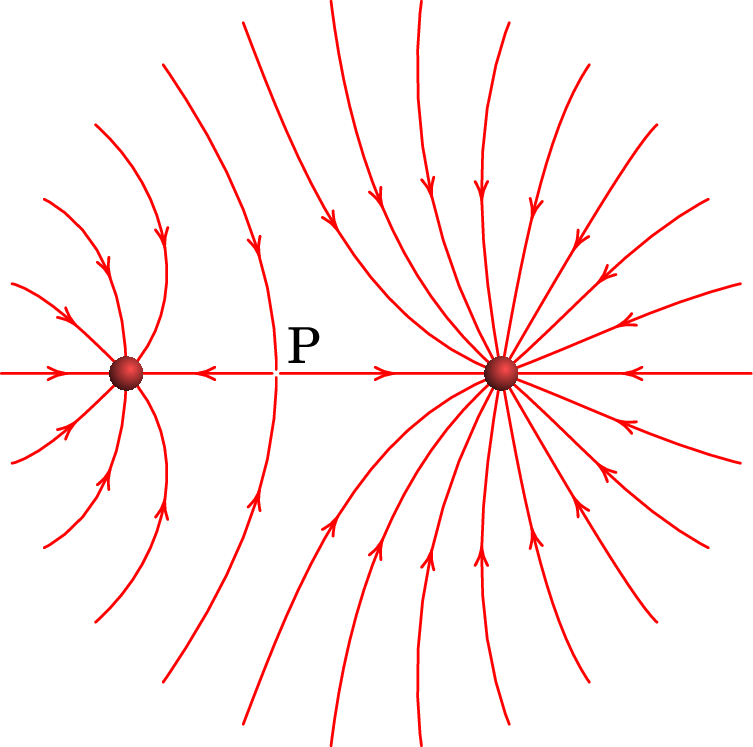
Resolução. (a) No ponto P o campo total é nulo, ou seja, os campos das duas cargas são vetores opostos e com o mesmo módulo. Se $d_{1}$ e $d_{2}$ são as distâncias desde cada uma das cargas até P, a condição para que os módulos dos dois campos sejam iguais é:

\dfrac{k\,|q_{1}|}{d_{1}^{2}}=\dfrac{k\,|q_{2}|}{d_{2}^{2}}\quad% \Longrightarrow\quad\dfrac{d_{1}}{d_{2}}=\sqrt{\dfrac{q_{1}}{q_{2}}}=\dfrac{2}% {3}

e como $d_{1}+d_{2}=7$ cm, então, com as distâncias em cm:

\dfrac{d_{1}}{7-d_{1}}=\dfrac{2}{3}\quad\Longrightarrow\quad d_{1}=\dfrac{14}{% 5}=2.8\;\mathrm{cm}

e $d_{2}=4.2$ cm. A carga mais próxima de P ( $q_{1}$ à esquerda) é menor que a outra ( $q_{2}$ à direita).

(b) A carga $q_{1}$ da partícula no lado esquerdo obtém-se a partir da outra carga $q_{2}=-8$ nC, usando a relação entre as cargas dada no enunciado:

\dfrac{q_{1}}{q_{2}}=\dfrac{4}{9}\quad\Longrightarrow\quad q_{1}=\dfrac{4\,q_{% 2}}{9}=\dfrac{32}{9}\;\mathrm{nC}

e o potencial total no ponto P é (unidades SI):

V=\dfrac{k\,q_{1}}{d_{1}}+\dfrac{k\,q_{2}}{d_{2}}=-\dfrac{8.988\times(32/9)}{0% .028}-\dfrac{8.988\times 8}{0.042}=-2853\,\mathrm{V}

Problema 3.5

Duas superfícies condutoras esféricas e concêntricas têm raios de 5 cm e 7 cm. A superfície menor tem carga total de 3 nC e a carga total na superfície maior é $-2$ nC. Qual é a diferença de potencial entre as duas superfícies?

Resolução. O potencial produzido por uma esfera condutora, de raio $R$ e carga total $Q$ , num ponto a uma distância $r$ do centro da esfera, é:

V(r)=\begin{cases}\dfrac{kQ}{r}&r\geq R\quad(\mbox{fora da esfera})\\[5.0pt] \dfrac{kQ}{R}&r<R\quad(\mbox{constante dentro})\end{cases}

Nos pontos na superfície com $R_{1}=5$ cm o potencial é a soma dos potenciais produzidos pelas duas esferas. Pontos esses que estão fora da esfera de raio $R_{1}$ e dentro da esfera de raio $R_{2}=7$ cm. Como tal,

V(R_{1})=\dfrac{kQ_{1}}{R_{1}}+\dfrac{kQ_{2}}{R_{2}}

Nos pontos na superfície com $R_{2}=7$ cm, fora das duas esferas, o potencial total é:

V(R_{2})=\dfrac{k\,Q_{1}}{R_{2}}+\dfrac{k\,Q_{2}}{R_{2}}

Como tal, em unidades SI, a diferença de potencial é

	$\displaystyle V(R_{1})-V(R_{2})$	$\displaystyle=\dfrac{kQ_{1}}{R_{1}}-\dfrac{kQ_{1}}{R_{2}}$
		$\displaystyle=3\times 10^{-9}\times 8.988\times 10^{-9}\left(\dfrac{1}{0.05}-% \dfrac{1}{0.07}\right)=154\,\mathrm{V}$

Comentários: A diferença de potencial é também o integral do campo elétrico desde uma esfera até a outra, em qualquer percurso, por exemplo, na direção radial $r$ . Na região de integração o campo é devido unicamente à esfera menor, porque essa região está dentro da esfera maior. Como tal,

V(R_{1})-V(R_{2})=\int_{R_{1}}^{R_{2}}\dfrac{kQ_{1}}{r^{2}}\,\mathrm{d}r=% \dfrac{kQ_{1}}{R_{1}}-\dfrac{kQ_{1}}{R_{2}}=154\,\mathrm{V}

Problema 3.6

A figura na capa deste livro é a representação gráfica das linhas de campo e superfícies equipotenciais do seguinte potencial sobre o plano $x y$ :

V(x,y)=\frac{a\,x}{(x^{2}+y^{2})^{3/2}}+\frac{b}{(x^{2}+y^{2})^{1/2}}

Explique a que tipo de sistema corresponde esse potencial e encontre a expressão do campo elétrico em qualquer ponto do plano $x y$ .

Resolução. O termo $(x^{2}+y^{2})^{1/2}$ é a distância até à origem, $r$ . Como o potencial de um dipolo na origem é

V(\vec{r})=\frac{k\,\vec{p}\cdot\vec{r}}{r^{3}}

então o primeiro termo é no potencial corresponde a um dipolo, com momento dipolar,

\vec{p}=(a/k)\,\hat{\imath}

O segundo termo no potencial, uma constante sobre a distância até à origem, corresponde ao potencial de uma carga pontual $b/k$ na origem. Como tal, o sistema é composto por um dipolo e uma carga pontual na origem.

O campo elétrico é menos o gradiente do potencial:

	$\displaystyle\vec{E}=$	$\displaystyle\biggl{(}-\dfrac{a}{(x^{2}+y^{2})^{3/2}}+\dfrac{3ax(2x)}{2(x^{2}+% y^{2})^{5/2}}+\dfrac{b(2x)}{2(x^{2}+y^{2})^{3/2}}\biggr{)}\,\hat{\imath}$
		$\displaystyle+\biggl{(}\dfrac{3ax(2y)}{2(x^{2}+y^{2})^{5/2}}+\dfrac{b(2y)}{2(x% ^{2}+y^{2})^{3/2}}\biggr{)}\,\hat{\jmath}$
	$\displaystyle=$	$\displaystyle\ \dfrac{bx^{3}+bxy^{2}-ay^{2}+2ax^{2}}{(x^{2}+y^{2})^{5/2}}\,% \hat{\imath}+\dfrac{by^{3}+bx^{2}y+3axy}{(x^{2}+y^{2})^{5/2}}\,\hat{\jmath}$

Problema 3.7

A figura mostra as superfícies equipotenciais de uma carga pontual no interior de um campo elétrico uniforme $\vec{E}_{\mathrm{ext}}$ . A grandes distâncias da carga pontual as superfícies são planos paralelos distanciados 8 cm.
(a) Calcule o módulo e a direção do campo externo $\vec{E}_{\mathrm{ext}}$ .
(b) Diga se a carga pontual é positiva ou negativa. Justifique.
(c) Qual é a direção da força sobre a carga pontual?
(d) Sabendo que a distância entre a carga pontual e o ponto P é 9 cm, calcule o valor da carga pontual.

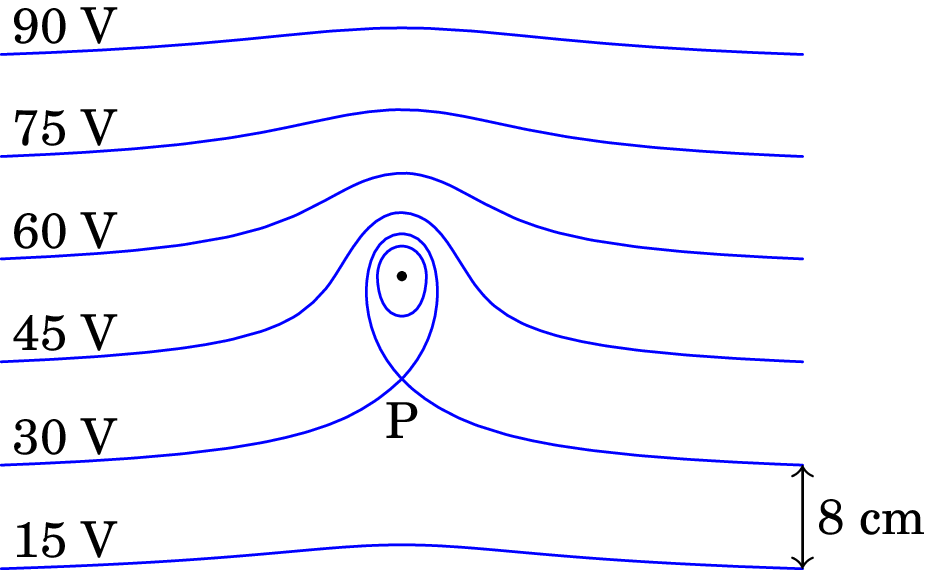
Resolução. (a) O campo externo aponta para baixo (direção em que diminui o potencial) e tem módulo:

E_{\text{ext}}=\dfrac{15}{0.08}=187.5\;\dfrac{\mathrm{V}}{\mathrm{m}}

(b) A carga é negativa, porque há uma linha de campo que atravessa as superfícies equipotenciais de 90 V, 75 V, 60 V, 45 V e 30 V entrando logo na carga. Também, se não existisse a carga pontual, o potencial no ponto onde se encontra teria um valor entre 45 V e 60 V, mas com a carga pontual o potencial nesse ponto passa a ser menor que 30 V, ou seja, o potencial da carga pontual é negativo e a carga também.

(d) No ponto P o campo total é nulo e, como tal, o módulo do campo produzido pela carga pontual deverá ser igual ao módulo do campo externo:

	$\displaystyle E$	$\displaystyle=\dfrac{k\,\|q\|}{d^{2}}=E_{\text{ext}}=187.5$
		$\displaystyle\Longrightarrow\quad\|q\|=\dfrac{187.5\times 0.09^{2}}{8.988\times 1% 0^{9}}=1.69\times 10^{-10}$

O valor da carga pontual é $q=-0.169$ nC.

Problema 3.8

Demonstre que o campo elétrico $\vec{E}=A\vec{r}$ , em que $A$ é uma constante e $\vec{r}$ o vetor posição, é conservativo. Calcule o potencial correspondente a esse campo.

Resolução. As componentes cartesianas do campo são:

E_{x}=Ax\qquad E_{y}=Ay\qquad E_{z}=Az

Todas as derivadas cruzadas são nulas e, portanto, iguais entre si:

\dfrac{\partial E_{x}}{\partial y}=\dfrac{\partial E_{y}}{\partial x}=\dfrac{% \partial E_{x}}{\partial z}=\dfrac{\partial E_{z}}{\partial x}=\dfrac{\partial E% _{y}}{\partial z}=\dfrac{\partial E_{z}}{\partial y}=0

a igualdade das derivadas cruzadas mostra que o campo é conservativo.

As três derivadas parciais do gradiente do potencial são:

\dfrac{\partial V}{\partial x}=-Ax\qquad\dfrac{\partial V}{\partial y}=-Ay% \qquad\dfrac{\partial V}{\partial z}=-Az

Como tal o potencial é,

V(x,y,z)=-\dfrac{A}{2}\bigl{(}x^{2}+y^{2}+z^{2}\bigr{)}=-\dfrac{Ar^{2}}{2}

(mais uma constante arbitrária que foi escolhida igual a zero, fazendo com que o potencial seja nulo na origem).