1. Introdução

1.1. Breve história da física quântica

1.1.1. Natureza da luz

A velocidade de um raio de luz tem sido medida com precisão, e o seu valor, no vácuo é,

c = 2.99792458 \times 10^{8} \frac{m}{s}

(1.1)

Num meio diferente do vácuo, a luz propaga-se com velocidade menor do que a sua velocidade $c$ no vácuo. Define-se o índice de refração de um material:

n = \frac{c}{v}

(1.2)

onde $v$ é a velocidade da luz nesse material. Como tal, $n$ será sempre maior que 1. O índice de refração do ar é aproximadamente 1.0003 e, como estamos a usar quatro algarismos significativos para as constantes, admitiremos que o índice de refração do ar é 1 (velocidade da luz no ar igual à velocidade da luz no vácuo).

Quando um raio de luz passa de um meio 1 para outro meio 2 como na figura 1.1, parte da luz é refletida no meio 1 e outra parte é refratada, passando para meio 2. O ângulo que o raio refratado faz com a perpendicular, $θ_{2}$ , é diferente do ângulo que o raio incidente faz com a perpendicular à superfície de separação entre os dois meios, $θ_{1}$ .

**Figure 1.1:** Refração de um raio de luz que passa de um meio para outro.

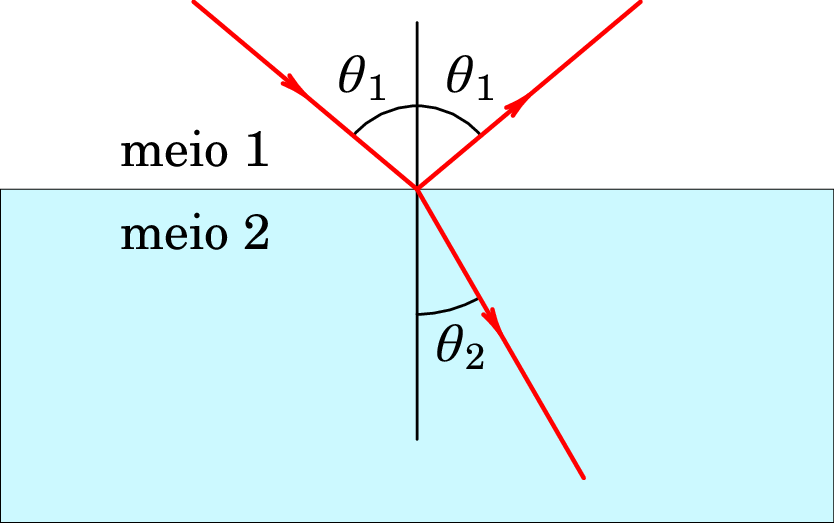
Mudando o ângulo $θ_{1}$ , observa-se que a relação,

n_{1} \sin θ_{1} = n_{2} \sin θ_{2}

(1.3)

designada por Lei de Snell.

A reflexão e refração da luz foram explicadas por Newton, admitindo que a luz é composta por pequenas partículas que se deslocam todas à velocidade da luz (teoria corpuscular da luz). O raio refletido corresponde às partículas que batem com a interface entre os dois meios; se a colisão é elástica, a as partículas são refletidas com o mesmo ângulo de incidência. O raio refratado são as partículas que conseguiram penetrar no meio 2, onde a velocidade da luz é diferente. Admitindo que as partículas que penetram mantêm a mesma componente da velocidade paralela à interface dos meios, mas a velocidade total é diferente, explica-se a lei de Snell e o índice de refração é a relação entre a velocidade da luz no vácuo e no meio. Como tal, no caso da figura1.1 em que $θ_{2} < θ_{1}$ , a velocidade da luz seria maior no meio 2 do que no meio 1, mas na prática acontece exatamente o oposto.

Huygens, contemporâneo de Newton, acreditava que a luz era uma onda, tal como o som, que corresponde a vibrações de um meio invisível, o éter. Nessa teoria ondulatória da luz consegue-se explicar também as leis da reflexão e da refração da luz, e o índice de refração resulta ser a relação entre a velocidade da luz no meio e a velocidade da luz no vácuo. Na época de Newton e Huygens (século XVIII), não era possível medir a diferença da velocidade da luz no vácuo e em outros meios, tais como a água ou o ar, e o grande sucesso da mecânica de Newton fez com que fosse dada maior credibilidade á teoria corpuscular da luz, em favor da teoria ondulatória.

No início do século XIX Thomas Young (1773–1829) deu o golpe de graça à teoria corpuscular da luz, com a sua experiência de interferência da luz que passa através de duas fendas muito próximas (figura 1.2).

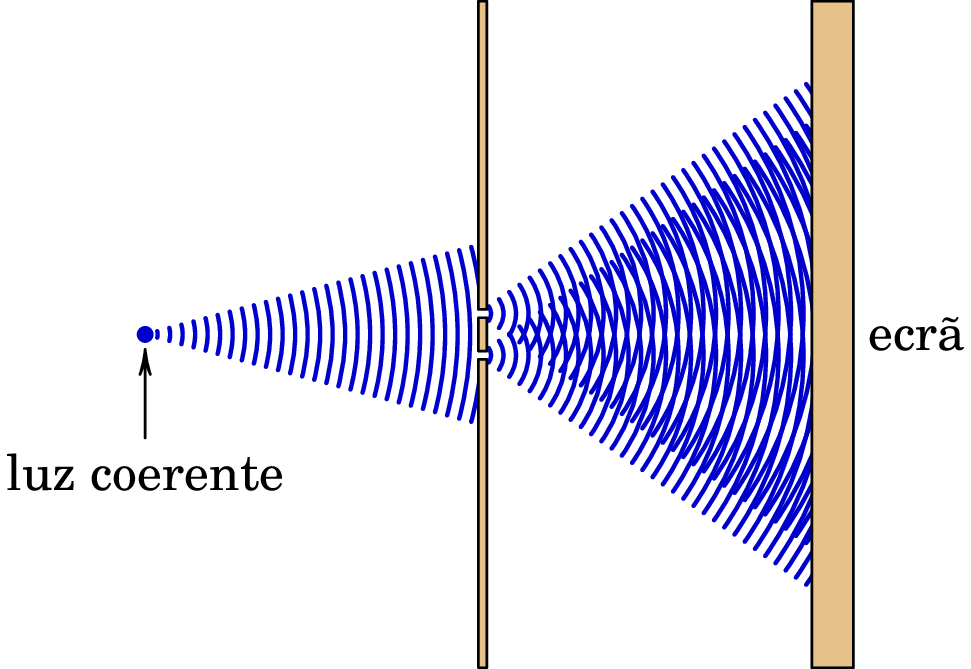
**Figure 1.2:** Interferência da luz após a passagem por duas fendas.

Se a luz fossem partículas, esperava-se que após a passagem pelas duas fendas, a maior parte delas chegassem ao ecrã próximas dos dois pontos exatamente em frente das duas fendas. No entanto, o que se observa são várias franjas claras e escuras no ecrã, que é um padrão de interferência caraterístico das ondas. Na figura 1.2 são visíveis essas zonas claras e escuras no ecrã. Nas zonas claras encontram-se as frentes de onda das duas ondas provenientes das duas fendas, produzindo interferência construtiva. Nas zonas escuras, uma frente de onda de uma das duas ondas (máximo) encontra-se com um ponto meio entre duas frentes de onda da segunda (mínimo), produzindo interferência destrutiva. O mesmo padrão de interferência é observado entre ondas de outros tipos, por exemplo, as ondas na superfície de um líquido, e a medição da distância entre as zonas claras e escuras permite determinar o comprimento de onda.

Ficou estabelecido que a luz era uma onda, e não composta por partículas como pensava Newton. Mas tarde, a meados do século XIX, James Maxwell demostrou que as equações do eletromagnetismo conduzem à possibilidade da existência de ondas eletromagnéticas: campos elétrico e magnético que se propagam em alguns materiais ou até no vácuo. A velocidade dessas ondas era dada em função das constantes elétrica e magnética, e o valor obtido coincide exatamente com a velocidade da luz no vácuo. Maxwell acreditava que a luz seria então uma onda eletromagnética; mas faltava mostrar que de facto era possível produzir ondas a partir dum sistema elétrico.

**Figure 1.3:** Espetro eletromagnético.

A primeira pessoa a conseguir produzir ondas eletromagnéticas no laboratório foi Heinrich Hertz, em 1877, oito anos após a morte de Maxwell. A partir de então foi possível realizar experiências com ondas eletromagnéticas e corroborar que têm as mesmas propriedades da luz. O espetro de ondas eletromagnéticas (figura 1.3) inclui vários tipos de ondas, e luz visível é a parte do espetro com comprimentos de onda entre 430 THz e 750 THz (comprimentos de onda entre 697 nm e 400 nm).

No fim do século XIX parecia ter sido resolvido o problema da natureza da luz, em favor da teoria ondulatória. No entanto a teoria ondulatória não conseguia explicar dois fenômenos: a radiação do corpo negro e o efeito fotoelétrico

1.1.2. Radiação do corpo negro

Um objeto aquecido produz luz. Se a temperatura não for muito elevada, a luz produzida não é visível mas está na região do infravermelho. Quando a temperatura aumenta, a luz passa a ser vermelha, e a temperaturas ainda maiores é praticamente branca. A luz que o objeto produz é realmente uma sobreposição de diferentes frequências que variam de forma contínua numa região do espetro eletromagnético.

Esse tipo de radiação é designado por radiação do corpo negro. A combinação da termodinâmica, que explica a relação entre a temperatura e a vibração das moléculas, junto com a teoria eletromagnética, que explica a produção de ondas eletromagnéticas por partículas com carga elétrica quando vibram, prevê que quase todo a luz produzida estaria na região do ultravioleta. Na prática o que se observa experimentalmente (figura 1.4) é que o espetro tem um máximo num comprimento de onda que depende da temperatura do corpo, e decresce na região do violeta. O fracasso da explicação teórica ficou conhecido como catástrofe do violeta.

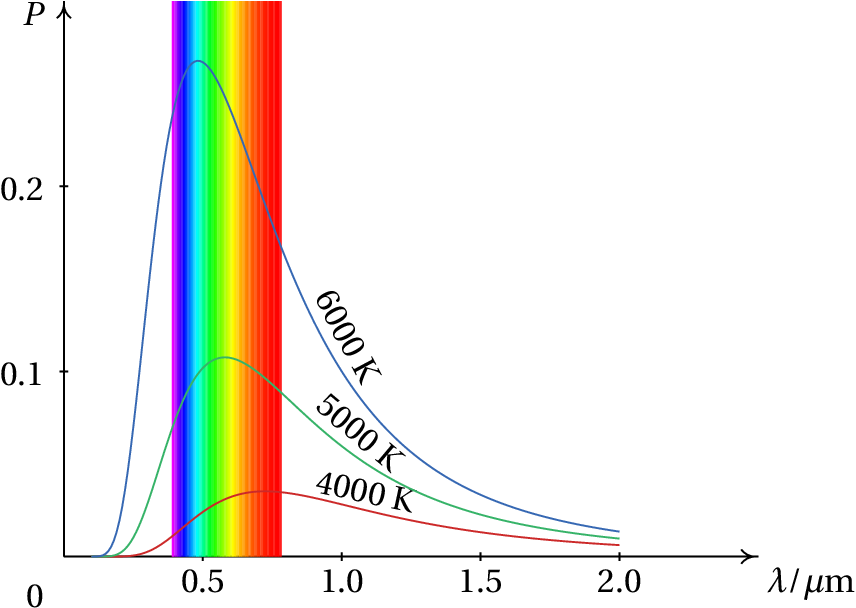
**Figure 1.4:** Potência emitida por um corpo negro, em função do comprimento de onda.

Max Planck trabalhou intensamente nesse problema, que implicava realizar alguns integrais em função da energia de oscilação das moléculas. Observou que quando aproximava esses integrais por somas em intervalos finitos de energia, o resultado era mais parecido ao espetro observado experimentalmente. Mas quando diminuía o tamanho dos intervalos, aparecia a catástrofe do violeta.

Em 1900 Planck postulou que a energia que as moléculas dum corpo podem libertar, devido à sua oscilação térmica, varia em múltiplos de um quantum de energia:

E = h f

(1.4)

onde $h$ é a constante de Planck, com valor,

h = 6.626 \times 10^{- 34} J \cdot s

(1.5)

e $f$ é a frequência de oscilação. Com esse postulado, Planck conseguia reproduzir de forma precisa o espectro observado experimentalmente.

1.1.3. Teoria dos fotões

Em 1905 Albert Einstein publicou um artigo em que argumenta que assim como um gás e outros tipos de matéria são considerados como um número finito de partículas, embora em número muito elevado, o campo eletromagnético, e em particular a luz, deveriam ser consideradas como um sistema discreto de partículas.

Einstein reconhece o grande sucesso da teoria ondulatória da luz para explicar os fenómenos da ótica, e não pensa que essa teoria deva ser abandonada, mas reconhece que as experiências de ótica têm a ver com valores médios no tempo e não com valores instantâneos, onde o caráter discreto da luz é mais importante e a teoria ondulatória falha.

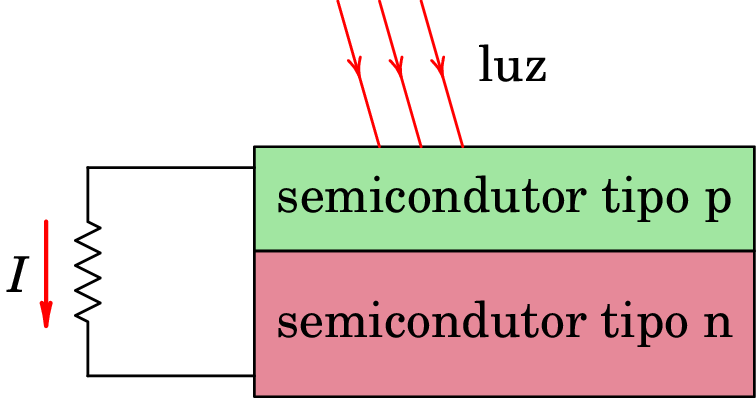
Um desses experimentos que não pode ser explicado pela teoria eletromagnética da luz é o efeito fotoelétrico, que consiste na emissão de eletrões em alguns metais quando são atingidos por luz, e que constitui a base das células fotovoltaicas em que a luz é usada para produzir energia (figura 1.5).

A velocidade dos eletrões libertados no efeito fotoelétrico não aumenta com o aumento da intensidade da luz, mas sim com o aumento da sua frequência; o aumento da intensidade da luz faz aumentar o número de eletrões mas não a sua velocidade. De facto, para cada material existe uma frequência por baixo da qual não se produz efeito fotoelétrico, independentemente da intensidade da luz. É como se tivéssemos um tsunami, com muita energia, que não produz nenhum dano num prédio, enquanto uma onda com amplitude e energia muito baixas, mas com frequência maior, destrói o mesmo prédio.

Einstein admite que a luz é formada por partículas, os fotões, e que a energia de cada fotão é igual à frequência vezes a constante de Planck: $h f$ . O quantum de energia $h f$ é o mesmo que foi considerado por Planck para explicar a radiação do corpo negro, mas agora não se trata apenas da energia libertada ou absorbida pelo corpo negro, mas a própria onda eletromagnética tem energia quantizada num número discreto de fotões.

A explicação dada por Einstein para o efeito fotoelétrico é que para libertar um eletrão no material, atingido por um fotão, a energia do fotão deverá ser superior à energia de ligação dos eletrões no material, $ϕ$ , designada por função de trabalho do material. O eletrão libertado terá energia cinética igual à diferença entre a energia do fotão absorvido, $h f$ , e a função de trabalho:

E = h f - ϕ

(se h f > ϕ)

(1.6)

isso explica porque existe uma frequência mínima para que ocorra o efeito fotoelétrico, e essa frequência mínima é igual à função de trabalho do material, dividida pela constante de Planck: $f_{mín} = ϕ / h$ .

Após o artigo revolucionário de Einstein foram realizadas mais experiências para estudar o efeito fotoelétrico. Numa dessas experiência mediu-se a energia com que são emitidos os eletrões, em função da frequência da luz, com resultados como os que mostra a figura 1.6.

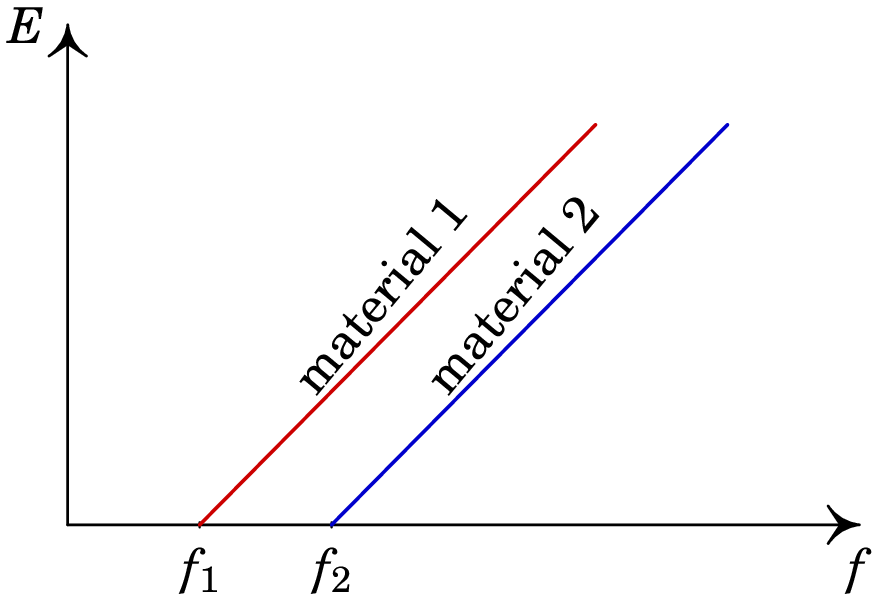
**Figure 1.6:** Energia dos eletrões libertados numa célula fotoelétrica, em função da frequência da luz incidente.

Com os resultados da figura 1.6 é possível corroborar que o declive da reta obtida para qualquer material fotoelétrico é exatamente igual à constante de Planck, tal como previa a equação (1.6). Hoje em dia, com uma célula fotoelétrica tal como a da figura 1.5 é possível reproduzir o gráfico 1.6, medindo a força eletromotriz da célula, usando luz com frequência que possa ser alterada, e multiplicando pela carga elementar para obter a energia dos eletrões emitidos.

Uma vez aceite, o conceito de fotão permitiu explicar muitos outros fenómenos bem conhecidos mas até então ignorados por não poder ser explicados pela teoria eletromagnética de Maxwell (fotoluminescência, calores específicos e até fotoquímica). A luz é assim caraterizada por uma dualidade onda-partícula: é produzida e absorvida em pacotes discretos de energia (fotões), mas o transporte dessa energia através do espaço é feito através de uma onda.

Mais tarde veio a descobrir-se que os eletrões, neutrões e outras partículas possuim também a dualidade onda-partícula. A pesar de serem consideradas partículas, exibem também fenómenos ondulatórios, tais como difração e interferência.

1.1.4. Estrutura atómica

Nos tubos de descarga elétrica, o gás dentro do tubo produz luz; a energia das colisões de eletrões e iões com o gás transferem energia para os átomos, que é logo libertada na forma de luz. De acordo com a teoria dos fotões, a energia é libertada pelos átomos do gás em fotões com energia $h f$ , proporcional à sua frequência $f$ . A análise espetral da luz produzida pelo tubo mostra que todos os fotões têm apenas umas poucas frequências discretas, caraterísticas de cada tipo de átomo. A parte superior da figura 1.7 mostra o espetro de emissão do hidrogénio, que é a decomposição espetral, nos diferentes comprimentos de onda, da luz produzida por um tubo de descarga com hidrogénio.

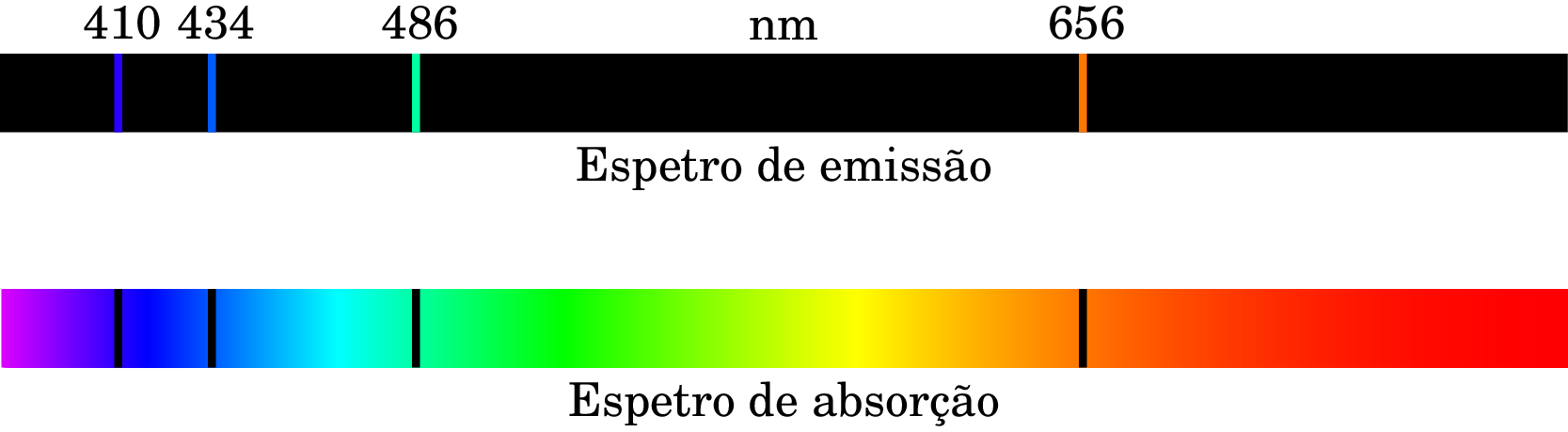
**Figure 1.7:** Espetros de emissão e de absorção do hidrogénio.

De forma análoga, quando luz branca, com todos os comprimentos de onda no espetro visível, atravessa um gás de hidrogénio, os átomos de hidrogénio absorvem os mesmos comprimentos de onda no espetro de emissão, como pode ver-se na parte inferior da figura 1.7 (espetro de absorção), que é a decomposição espetral da luz após a passagem pelo gás; as riscas pretas indicam os comprimentos de onda dos fotões que são absorvidos pelo hidrogénio.

As riscas nos espectros de emissão ou absorção são como a "impressão digital" dos diferentes átomos. Têm sido usadas para determinar os elementos que compõem as estrelas, através da análise espetral da luz que emitem. Os comprimentos de onda, $λ$ , no espetro do hidrogénio da figura 1.7 são obtidos por meios óticos, e permitem-nos determinar as energias dos respetivos fotões:

E = h f = \frac{h c}{λ}

(1.7)

Substituindo a constante de Planck e a velocidade da luz no vácuo, e dividindo a energia obtida pelo valor da carga elementar ( $1.602 \times 10^{- 19}$ C), para expressar essas energias em eletrão-volts, obtêm-se os valores: 3.02 eV, 2.86 eV, 2.55 eV, 1.89 eV. Valores esses que devem corresponder à diferença entre a energia inicial do átomo e a sua energia após absorver um fotão com o respetivo comprimento de onda. O lado esquerdo da figura 1.8 mostra a relação desses níveis de energia, arbitrando a energia inicial igual a 0.

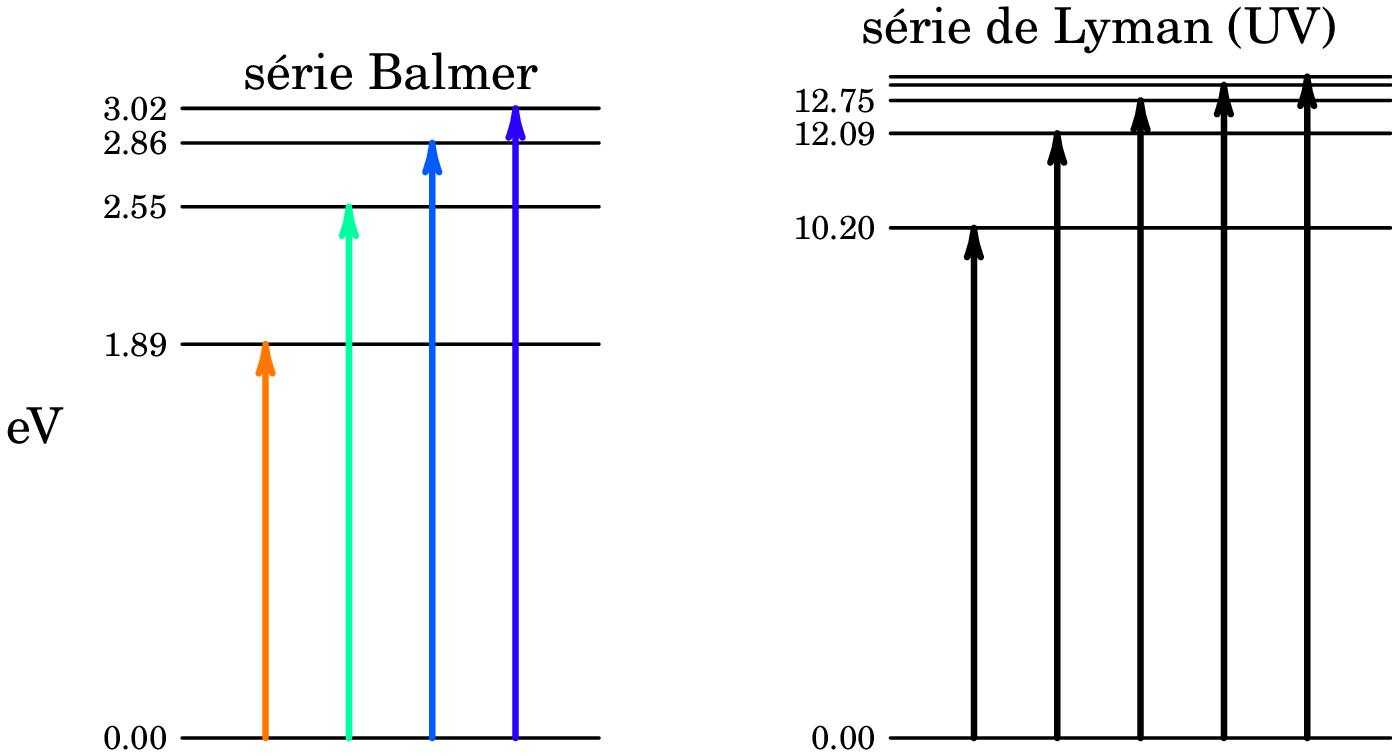
**Figure 1.8:** Séries espetrais do átomo de hidrogénio.

Outras series espectrais foram descobertas para o átomo de hidrogénio, nas regiões ultravioleta e infravermelha do espetro. A figura 1.8 mostra a série na região visível do espetro, designada por série de Balmer, e a série na região ultravioleta, designada por série de Lyman. Observe-se que a diferença entre o segundo e terceiro níveis de energia na série de Lyman é exatamente igual à diferença entre os dois primeiros níveis na série de Balmer, e as outras 3 diferenças entre níveis de energia consecutivos na série de Balmer também corresponde a diferenças de energia entre níveis consecutivos na série de Lyman. Podemos assim representar os níveis das duas séries no diagrama comum da figura 1.9, onde encaixa também a série espetral no infravermelho (série de Paschen).

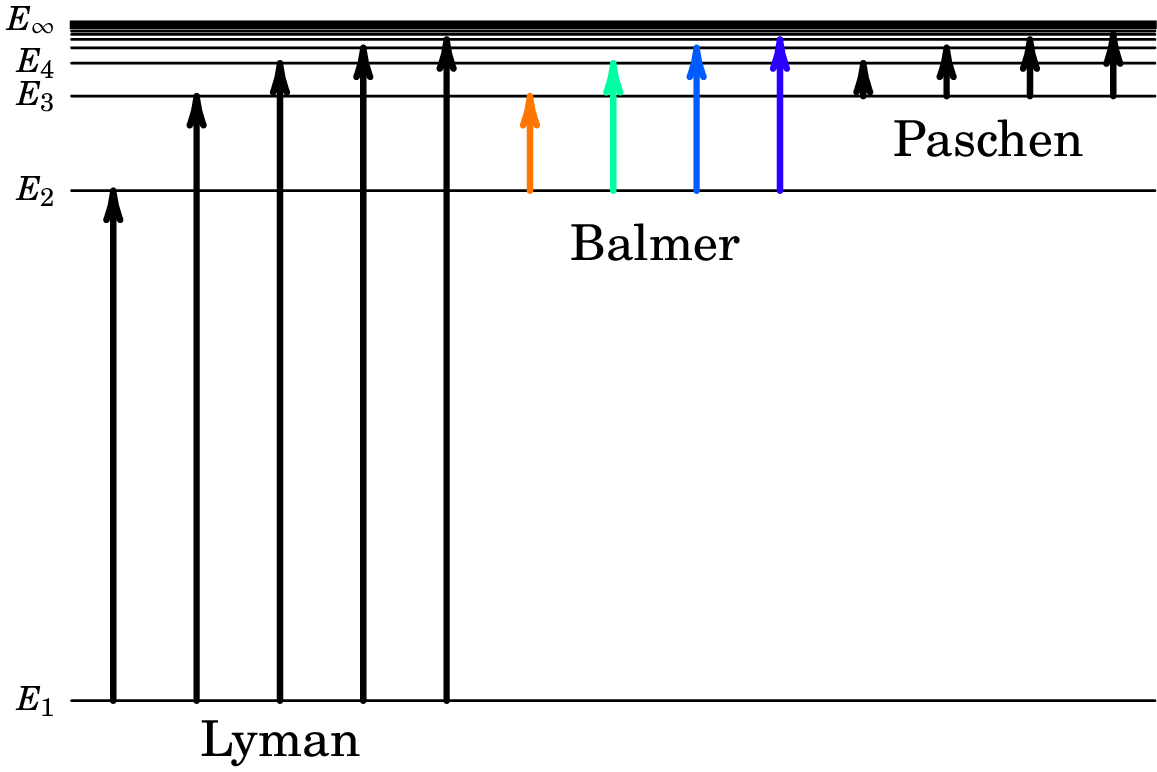
**Figure 1.9:** Níveis de energia do átomo de hidrogénio.

Conclui-se que as séries do espetro de absorção correspondem à passagem dos átomos de hidrogénio do seu nível mais baixo de energia, $E_{1}$ para niveis superiores, $E_{j}$ ( $j > 1$ ), após absorverem um fotão de energia igual $E_{j} - E_{1}$ . Os átomos podem primeiro absorver um fotão, passando do nível $E_{1}$ para o nível $E_{2}$ , e a seguir absorver outros fotões com energias $E_{j} - E_{2}$ ( $j = 3, 4, 5, 6$ ), dando origem à série de Balmer, na região visível do espetro.

Os níveis com energias superiores aproxima-se dum valor $E_{\infty}$ , que deverá ser a energia máxima que pode absorver o átomo até se desfazer. Como tal, $E_{\infty}$ corresponde ao estado em que a energia de ligação do átomo é nula, e arbitrando $E_{\infty} = 0$ , observa-se que nos outros níveis a energia de ligação do átomo segue a seguinte sucessão aritmética simples:

E_{n} = - \frac{R y}{n^{2}}

n = 1, 2, 3, \dots

(1.8)

onde $n$ é um número natural $n = 1, 2, 3$ , …, e $R y$ é a constante de Rydberg, com valor:

R y = 13.60 e V

(1.9)

Em 1913, Niels Bohr conseguiu explicar a sucessão dos níveis energéticos do átomo de hidrogénio, usando um modelo muito simples. Como o núcleo do átomo de hidrogénio (um protão) tem raio 5 ordens de grandeza menor do que o átomo, e massa aproximadamente 2000 vezes maior que a massa do eletrão, no modelo de Bohr admite-se que o núcleo é uma carga pontual fixa no centro do átomo, e o eletrão é outra carga pontual numa órbita circular à volta do núcleo, mas só pode estar em algumas possíveis órbitas. Cada nível de energia corresponde à energia do eletrão numa dessas órbitas. Bohr consegue reproduzir a expressão (1.8) admitindo apenas que o integral da quantidade de movimento do eletrão ao longo da órbita deverá ser um múltiplo inteiro da constante de Planck:

\oint_{órbita} m \vec{v} \cdot d \vec{r} = n h

(1.10)

A condição de quantização (1.10) conduz também aos raios das possíveis órbitas do eletrão:

r_{n} = a_{0} n^{2}

n = 1, 2, 3, \dots

(1.11)

em que $a_{0}$ , designado por raio de Bohr, é igual ao raio da órbita mais próxima do núcleo, com valor,

a_{0} = 0.5293 \times 10^{- 10} m

(1.12)

que coincide com o valor estimado experimentalmente para o raio de um átomo de hidrogénio. O átomo só absorve ou emite fotões com níveis discretos de comprimentos de onda, porque pode sofrer transições apenas entre as possíveis órbitas com níveis discretos de energia.

A conclusão dos fenómenos descritos nas secções anteriores é que a física clássica consegue explicar os casos em que a escala de energias é elevada, por exemplo, da ordem dos joule. Quando a transferência de energia é da ordem dos eletrão-volt, essa transferência só pode acontecer em níveis discretos, e estaremos no domínio de uma nova física, a física quântica. Vários modelos quânticos foram propostos para reproduzir os resultados de diferentes experiências, e uma teoria consistente que explica todos esses fenómenos foi proposta por Max Born e outros físicos, em 1925.

Antes de proceder a explicar os fundamentos dessa teoria, é conveniente fazer uma revisão da álgebra de números complexos, e da teoria das probabilidades, que são dois ingredientes importantes nessa teoria.

1.2. Números complexos

A forma retangular dum número complexo $z$ é

z = x + i y

(1.13)

onde $x$ (parte real) e $y$ (parte imaginária) são dois números reais, no campo dos números reais, $i = \sqrt{- 1}$ , e o produto $i y$ representa um número imaginário. A figura 1.10 mostra o chamado plano complexo, que é um plano onde cada ponto corresponde a um número complexo $z$ ; as suas partes real e imaginária são as projeções $x$ e $y$ em dois eixos perpendiculares, designados de Re (eixo real) e Im (eixo imaginário).

**Figure 1.10:** Número complexo $z = x + i y$ representado no plano complexo.

Definem-se o módulo $| z |$ e o argumento $φ$ do número complexo $z$ :

| z | = \sqrt{x^{2} + y^{2}} φ = A r c t a n (x, y)

(1.14)

onde $A r c t a n (x, y)$ é a função \concept{tangente inversa nos 4 quadrantes}, definida por,

A r c t a n (x, y) = {\begin{matrix} \arctan (\frac{y}{x}) + π & x < 0, y \geq 0 \\ \arctan (\frac{y}{x}) & x \geq 0 \\ \arctan (\frac{y}{x}) - π & x < 0, y < 0 \end{matrix}

(1.15)

onde $A r c t a n$ é a função definida em (1.15) e o argumento está no intervalo $- π < φ \leq π$ .

No plano complexo, $| z |$ é a distância desde o ponto onde se encontra $z$ , até à origem e $φ$ é o ângulo que o segmento desde $z$ até à origem faz com o semieixo Re positivo (ver figura 1.10).

O número complexo $z$ pode então ser escrito também na chamada forma polar,

z = | z | (\cos φ + i \sin φ)

(1.16)

A função complexa entre parêntesis na equação (1.16) costuma ser designada $c i s (φ)$ , ou ainda, $e^{i φ}$ , por ter propriedades semelhantes à função exponencial real $e^{x}$ . Para mostrar mais facilmente algumas operações entre números complexos, escreveremos a forma polar usando a função exponencial:\footnote{A expressão $e^{i φ} = (\cos φ + i \sin φ)$ é designada de fórmula de Euler.}

z = | z | e^{i φ}

(1.17)

A soma de dois números complexos, $z_{1} = x_{1} + i y_{1}$ e $z_{2} = x_{2} + i y_{2}$ , é outro número complexo, $z_{1} + z_{2}$ , com partes real e imaginária iguais à soma das respetivas partes dos dois números:

z_{1} + z_{2} = (x_{1} + x_{2}) + i (y_{1} + y_{2})

(1.18)

esta é a mesma forma da soma de dois vetores no plano $x y$ , em função das suas componentes. Como tal, a soma de números complexos segue a mesma regra do paralelogramo, no plano complexo, do que a soma de vetores, como mostra a figura 1.11. E a soma de números complexos tem as mesmas propriedades da soma de vetores.

**Figure 1.11:** Adição de números complexos no plano complexo.

Em contraste com os vetores, no caso dos números complexos é possível definir um produto que dá como resultado outro número complexo e tem as mesmas propriedades do produto entre números reais (comutatividade, associatividade, distributividade, etc.). O produto entre dois números complexos, $z_{1} = x_{1} + i y_{1}$ e $z_{2} = x_{2} + i y_{2}$ , é outro número complexo, $z_{1} z_{2}$ , que pode ser obtido usando a sua propriedade distributiva e o facto de que $i^{2} = - 1$ :

z_{1} z_{2} = (x_{1} + i y_{1}) (x_{2} + i y_{2})

= x_{1} x_{2} + i^{2} y_{1} y_{2} + i x_{1} y_{2} + i x_{2} y_{1}

= (x_{1} x_{2} - y_{1} y_{2}) + i (x_{1} y_{2} + x_{2} y_{1})

(1.19)

Produto este que tem uma expressão mais simples em termos das componentes polares dos números complexos:

z_{1} z_{2} = | z_{1} | | z_{2} | e^{i (φ_{1} + φ_{2})}

(1.20)

Ou seja, o produto $z_{1} z_{2}$ tem módulo igual ao produto dos módulos de $z_{1}$ e $z_{2}$ e argumento igual à soma dos argumentos de $z_{1}$ e $z_{2}$ . E a divisão é feita dividindo os módulos e subtraindo os argumentos:

\frac{z_{1}}{z_{2}} = \frac{| z_{1} |}{| z_{2} |} e^{i (φ_{1} - φ_{2})}

(1.21)

Define-se o conjugado, $z^{⋆}$ , do número $z$ , mantendo o módulo igual mas trocando o sinal do argumento:

z^{⋆} = | z | e^{- i φ} = x - i y

(1.22)

A conjugação de números complexos tem as seguintes propriedades:

O conjugado do conjugado é igual ao número inicial:
${(z^{⋆})}^{⋆} = z$
(1.23)
O produto de um número complexo com o seu conjugado é igual ao seu módulo ao quadrado:
$z z^{⋆} = z^{⋆} z = | z |^{2}$
(1.24)
Se o conjugado de um número complexo for igual a si próprio, é equivalente a dizer que o número é real (parte imaginária nula):
$z^{⋆} = z ⟺ z é real$
(1.25)
O conjugado da soma de dois números complexos é igual à soma dos conjugados dos números:
$(z_{1} + z_{2})^{⋆} = z_{1}^{⋆} + z_{2}^{⋆}$
(1.26)
O conjugado do produto de dois números complexos é igual ao produto dos conjugados dos números:
$(z_{1} z_{2})^{⋆} = z_{1}^{⋆} z_{2}^{⋆}$
(1.27)

1.3. Teoria das probabilidades

Uma experiência é dita aleatória, se não conseguirmos prever o valor obtido para certas variáveis, de forma que o resultado poderá ser diferente para várias repetições da mesma experiência. Um exemplo é o lançamento de uma moeda ou de um dado; a cada lançamento não conseguimos prever se o resultado da moeda será cara ou coroa, ou qual dos seis números ficará na fase superior do lado.

Tal vez se soubéssemos com precisão os valores de alguns parámetros, tais como posição e velocidade inicial do dado, velocidade, temperatura e pressão em todos os pontos do ar na trajetória do dado, etc., seria possível prever o resultado. Mas são muitas variáveis que podem afetar o resultado e um pequeno erro na medição de algumas dessas variáveis pode conduzir a uma previsão errada. No caso da mecânica quântica veremos que existem experiências realmente aleatórias, em que acreditamos que é impossível prever o resultado exato.

Se os possíveis resultados da experiência aleatória forem ${a_{1}, a_{2}, & h e l l i p;, a_{n}}$ . Se a experiência for repetida um número elevado de vezes, $N$ , a probabilidade $P (a_{i})$ de que o resultado $a_{i}$ seja obtido é igual ao número de vezes que o resultado foi $a_{i}$ , dividido pelo número de repetições $N$ . Como tal, a soma das probabilidades de todos os possíveis resultados é igual a 1:

\sum_{i = 1}^{n} P (a_{i}) = P (a_{1}) + P (a_{2}) + \dots + P (a_{n}) = 1

(1.28)

No caso do lançamento do dado, os possíveis resultados são ${1, 2, 3, 4, 5, 6}$ e a probabilidade de cada um desse resultados é $1 / 6$ .

O conjunto de possíveis resultados pode ser um conjunto contínuo; por exemplo, uma variável $x$ que pode ter qualquer valor entre $x_{1}$ e $x_{2}$ . Nesse caso há uma função contínua $P (x)$ tal que a probabilidade do resultado estar num pequeno intervalo entre $a$ e $b$ (com $a$ e $b$ entre $x_{1}$ e $x_{2}$ ) é igual a,

P (a < x < b) = \int_{a}^{b} P (x) d x

(1.29)

E o integral de $P (x)$ no intervalo de possíveis valores é igual a 1:

\int_{x_{1}}^{x_{2}} P (x) d x = 1

(1.30)

Se uma função $f$ associa um valor $f (a_{i})$ a cada possível resultado $a_{i}$ , a probabilidade da função ter o valor $f (a_{i})$ é igual a $P (a_{i})$ . O valor médio da função, ou valor esperado, é obtido somando os possíveis valores de $f$ vezes as respetivas probabilidades:

⟨ f ⟩ = \sum_{i = 1}^{n} f (a_{i}) P (a_{i})

(1.31)

Para determinar que tão dispersos estão os possíveis valores de $f (a_{i})$ e relação ao valor esperado $⟨ f ⟩$ , define-se a variança da função $f$ , igual ao valor esperado do desvio quadrático em relação ao valor esperado:

(Δ f)^{2} = ⟨ (f - ⟨ f ⟩)^{2} ⟩ = \sum_{i = 1}^{n} {(f (a_{i}) - ⟨ f ⟩)}^{2} P (a_{i})

(1.32)

e o desvio padrão é a raiz quadrada da variança:

Δ f = \sqrt{⟨ (f - ⟨ f ⟩)^{2} ⟩}

(1.33)

Exercícios

1.1. Usando a condição de quantização de Bohr, equação (1.10), encontre as expressões dos raios e energias das órbitas circulares do eletrão no átomo de hidrogénio, e determine os valores do raio de Bohr e da constante de Rydberg.

Resolução. A força centrípeta responsável pelo movimento circular do eletrão é a força elétrica entre o protão e o núcleo, dada pela lei de Coulomb:

F = \frac{k e^{2}}{r^{2}}

em que $e$ é a carga elementar e $k$ a constante de Coulomb. Igualando essa expressão à massa do eletrão, $m$ , vezes a sua aceleração centrípeta, encontra-se a seguinte relação entre a velocidade e o raio do eletrão:

\frac{k e^{2}}{r^{2}} = m \frac{v^{2}}{r} ⟹ m v^{2} = \frac{k e^{2}}{r}

(1.34)

O produto escalar $\vec{v} \cdot d \vec{r}$ no integral (1.10) é igual ao módulo da velocidade, $v$ , que é constante na órbita circular, vezes o comprimento de arco, $d s$ , da órbita circular. A condição de quantização (1.10) conduz a uma relação entre os valores discretos de $v$ e $r$ :

\oint_{órbita} m \vec{v} \cdot d \vec{r} = m v \oint_{órbita} d s = 2 π r m v = n h

⟹ v = \frac{n ℏ}{m r}

onde $ℏ$ é igual à constante de Planck dividida por $2 π$ , com valor:

ℏ = 1.055 \times 10^{- 34} \frac{k g \cdot m^{2}}{s}

(1.35)

Substituindo na equação (1.34), obtém-se a expressão dos raios da possíveis órbitas:

r_{n} = \frac{ℏ^{2}}{m k e^{2}} n^{2}

(1.36)

e, como tal, a expressão do raio de Bohr é:

a_{0} = \frac{ℏ^{2}}{m k e^{2}}

(1.37)

e com os valores da constante de Planck, massa do eletrão, constante de Coulomb e carga elementar, obtém-se o valor dado na expressão(1.12).

A energia mecânica do eletrão é a sua energia cinética mais energia potencial elétrica:

E = \frac{1}{2} m v^{2} - \frac{k e^{2}}{r} = - \frac{k e^{2}}{2 r}

onde foi usada a relação (1.34). Substituindo a expressão (1.36) do raio no nivel $n$ , obtém-se a energia do nível $n$ :

E_{n} = - \frac{k e^{2}}{2 a_{o} n^{2}}

e usando a expressão (1.37) do raio de Bohr, obtém-se a expressão da constante de Rydberg:

R y = \frac{m k^{2} e^{4}}{2 ℏ^{2}}

(1.38)

que, em unidades de eletrão-volt, é igual a $13.60$ eV.

1.2. Determine o resultado da seguinte expressão:

\frac{[(2 - i 3) + (- 1 + i 7)] (3 - i 2)}{2 + i 3}

Resolução. Começamos por realizar a soma entre os parênteses retos, e a seguir o produto no numerador:

(2 - i 3) + (- 1 + i 7) = 1 + i 4

(1 + i 4) (3 - i 2) = 11 + i 10

Para dividir o numerador pelo denominador, podemos multiplicar o numerador e denominador pelo conjugado complexo do denominador, para ficarmos com um número real no denominador:

\frac{11 + i 10}{2 + i 3} = \frac{(11 + i 10) (2 - i 3)}{(2 + i 3) (2 - i 3)} = \frac{52 - i 13}{4 + 9} = 4 - i

1.3. Num jogo de cartas, o jogador A baralha as 52 cartas e o jogador B escolhe uma carta qualquer. Se a carta escolhida for um número par, o jogador B paga 3 euros ao jogador A, se for um número ímpar, o jogador A paga 1 euro ao jogador B, e se a carta for um ás o jogador A paga 10 euros ao jogador B. A carta escolhida é reposta no baralho e o jogo repete-se. Qual dos dois jogadores tem maior probabilidade de ganhar mais dinheiro após várias repetições do jogo e qual o valor médio que ganhará após várias jogadas?

Resolução. Em cada grupo de 13 cartas há um ás, 5 cartas com número par (2, 4, 6, 8 e 10), e 4 cartas com número ímpar (3, 5, 7 e 9). Como tal, as probabilidades de o jogador B retirar um ás, um número par ou um número ímpar são:

P (a) = \frac{1}{13} P (p) = \frac{5}{13} P (i) = \frac{4}{13}

e o que o jogador B ganha/perde se a carta escolhida for um ás, número par, ou número ímpar é:

G (a) = 10 G (p) = - 3 G (i) = 1

O valor esperado do ganho do jogador B, cada vez que escolhe uma carta, é então:

⟨ G ⟩ = G (a) P (a) + G (p) P (p) + G (i) P (i)

= \frac{10}{13} - \frac{15}{13} + \frac{4}{13} = - \frac{1}{13}

Ou seja, quem tem maior probabilidade de ganhar é o jogador A, e em média ganha 1/13 euros a cada jogada. Após várias jogadas, terá ganho em média o número de jogadas divididas por 13, em euros.

1.4. Num teste com 20 perguntas de escolha múltipla, cada pergunta tem 5 possíveis respostas. A cotação é de um valor por cada resposta correta e zero valores se a pergunta não for respondida ou respondida de forma errada. Se os estudantes respondem todas as perguntas, selecionando de forma aleatória a resposta das perguntas que não sabem responder: (a) Entre que valores espera-se que esteja a nota dos estudantes? (b) Quantos valores deveriam ser descontados por cada resposta errada, para que a nota esperada estivesse compreendida entre 0 e 20?

Resolução. (a) A nota máxima, de um estudante que sabe responder a todas as perguntas, é 20. A nota mínima, de um estudante que responde todas as perguntas de forma aleatória, sera o número de respostas corretas, que em média será 1/5 do número total de perguntas. Como tal, a nota esperada dos estudantes estará entre 4 e 20 valores.

(b) Para que a nota esperada esteja entre 0 e 20 valores, há que garantir que o valor esperado da cotação de cada pergunta seja igual a zero, para que as perguntas respondidas de forma aleatória tenham um valor total nulo. Como nas 5 possíveis respostas há uma correta, com cotação de 1 valor, as restantes 4 respostas erradas deverão ter uma cotação total de $- 1$ valor. Cada resposta errada deverá descontar $0.25$ valores.