O sistema de Rössler é definido pelas seguintes equações de evolução, com 3 parâmetros positivos , e :
Investigue a solução do sistema com
e
fixos e com os
seguintes valores de
: (a)
(b)
(c)
(d)
.
Em cada caso use o programa rk para obter a solução, com
incrementos de tempo
e de forma a que sejam feitas
6000 iterações. Pode usar como valores iniciais
. Trace os
gráficos da curva projetada no plano
e de
em função de
. Volte a executar 6000 iterações do programa rk, mas agora
usando como valores iniciais os valores finais obtidos na primeira
execução do programa (o comando rest (last
(lista )) extrai o último vetor na lista
anterior, excluindo o tempo). Trace novamente os mesmos gráficos e
repita o procedimento até conseguir concluir qual é o conjunto limite
positivo da curva considerada e se for um ciclo, determine o seu
período. Em cada alínea diga qual é o conjunto limite, o seu
período (se for um ciclo) e mostre um gráfico que justifique a sua
conclusão.
(a) Os quatro comandos seguintes do Maxima definem uma lista com as expressões nos três lados direitos das equações de evolução, com os parâmetros , e . A seguir, usa-se o programa rk usando a lista anterior para definir a velocidade de fase, com variáveis de estado ( , , ), valores iniciais (2, 2, 2) e incrementos de tempo iguais a 0.01. Como o sistema é autónomo, o valor inicial de pode ser qualquer, por exemplo, 0; com esse valor inicial, o valor final de deverá ser 60, para que sejam executadas 6000 iterações. A solução, na lista sol, usa-se para traçar os gráficos da sua projeção no plano e de em função de . A seguir aos comandos mostram-se os gráficos obtidos.
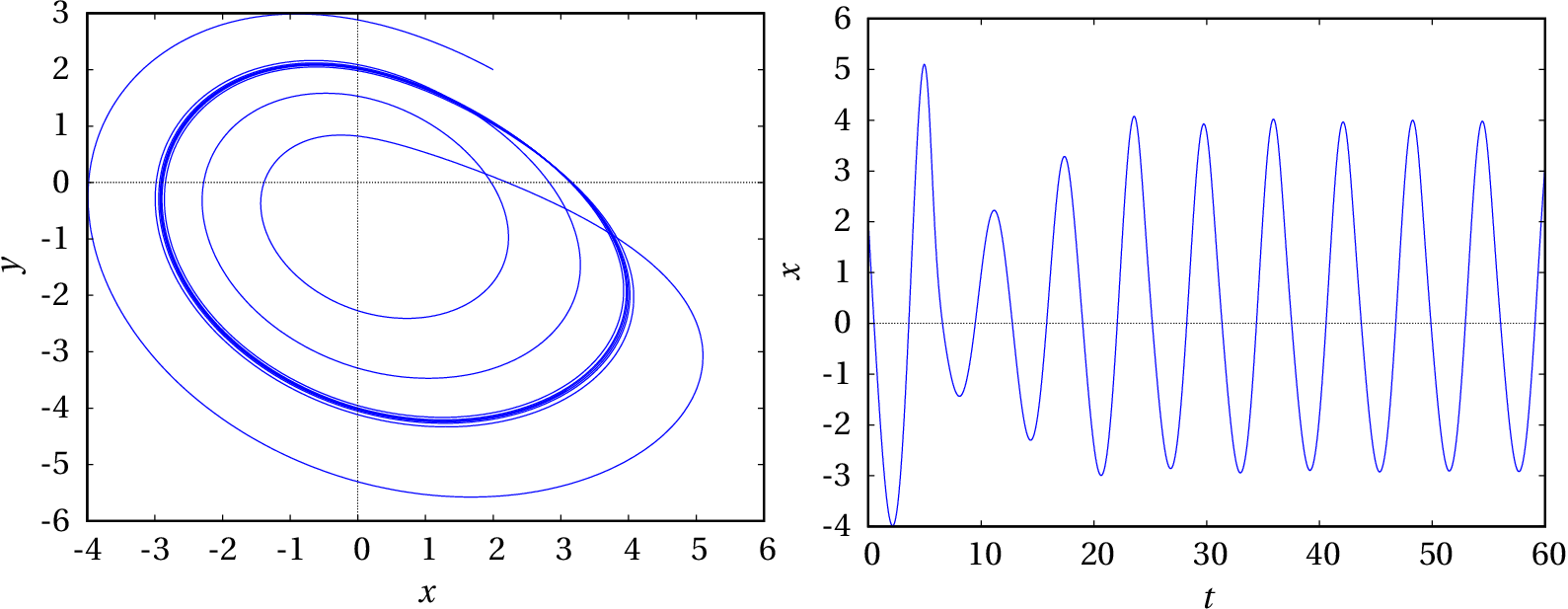
Para saber se a curva de evolução já está próxima do seu conjunto limite positivo, convém executar os mesmos comandos anteriores, usando agora como valores iniciais os valores finais da última iteração, para observar a continuação da curva no próximo intervalo .
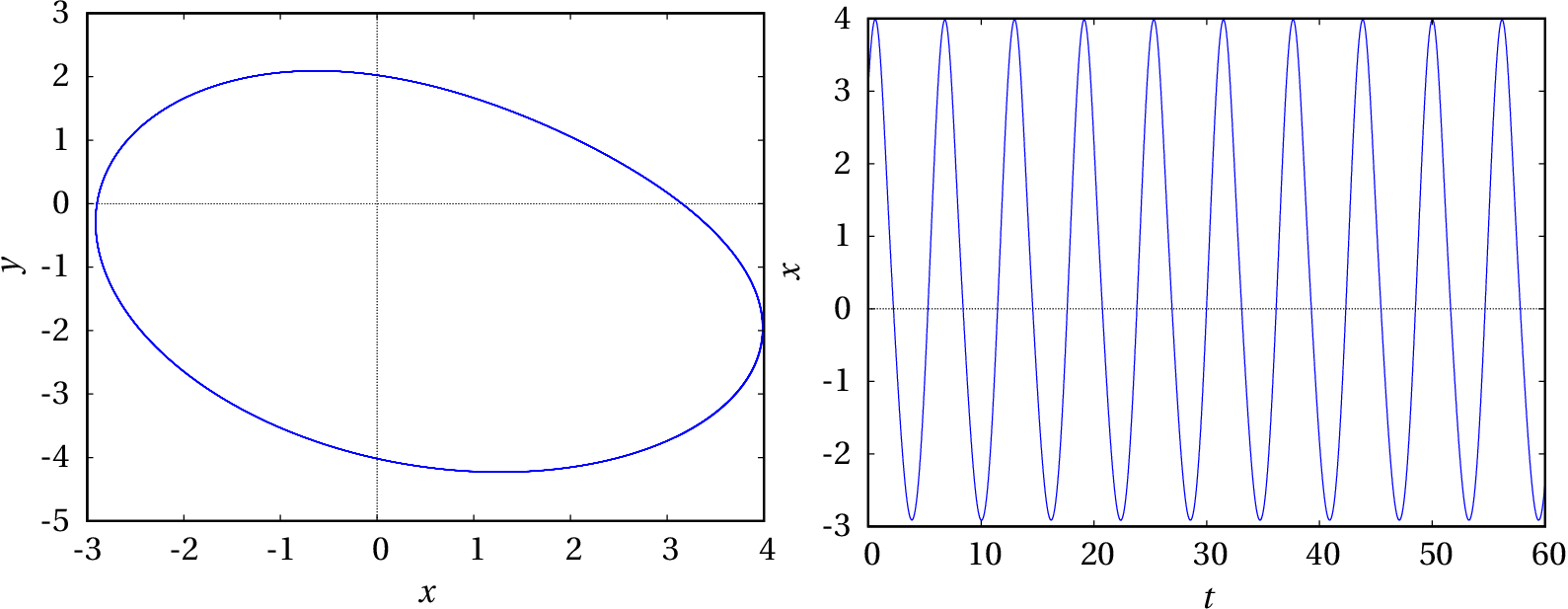
Estes últimos gráficos mostram que o sistema entrou num ciclo limite atrativo (conjunto limite positivo). O período desse ciclo pode obter-se, de forma aproximada, colocando o cursor por cima de dois dos valores máximos no gráfico de e registando os valores de indicados pelo Maxima. Convém usar dois máximos que estejam o mais afastados possível no gráfico e dividir pelo número de oscilações entre esses dois máximos. No gráfico acima, com 9 oscilações, o valor medido para o período é:
(b) Com , repete-se o mesmo procedimento da alínea anterior.
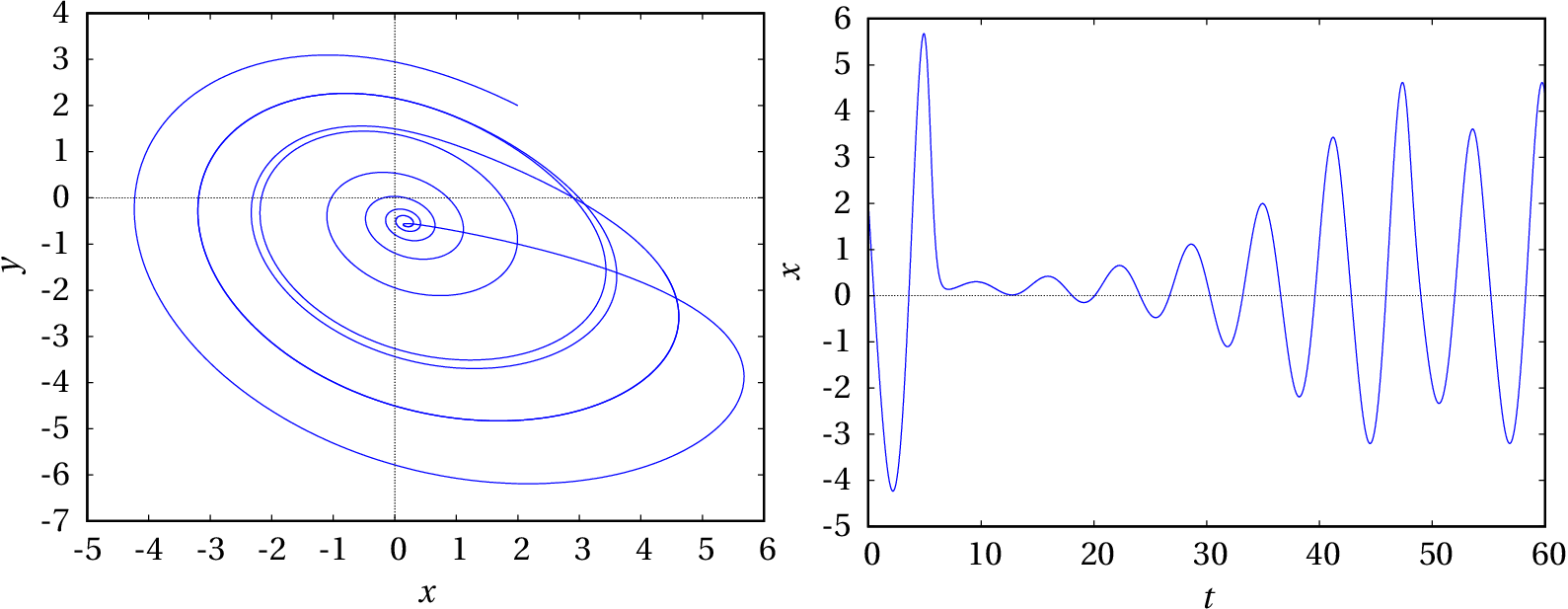
E mais 6000 iterações a partir dos valores finais das variáveis de estado após as primeiras 6000 iterações.
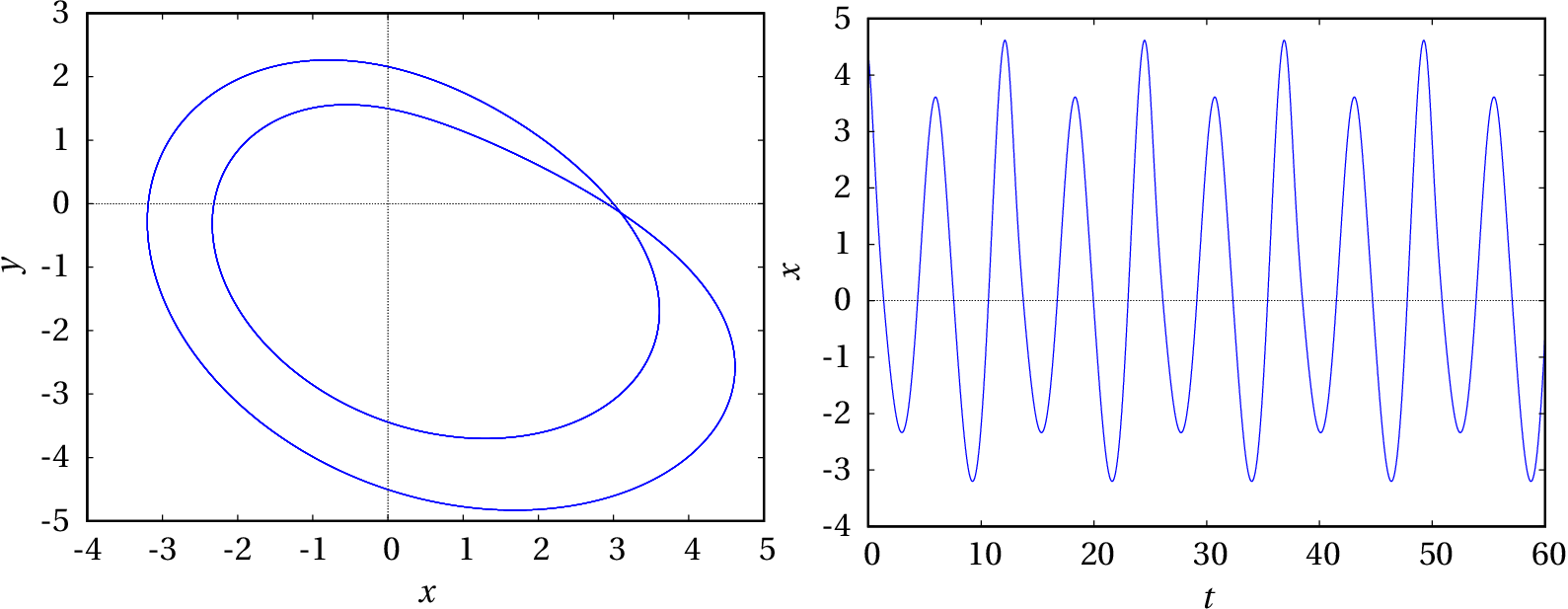
O sistema entrou novamente num ciclo limite atrativo (conjunto limite positivo), que dá duas voltas no espaço de fase antes de se repetir. No gráfico de observam-se 4 oscilações completas, cada uma com dois máximos locais e dois mínimos locais. O valor medido para o período é:
que é aproximadamente o dobro do período no ciclo simples obtido com . Diz-se que existe uma bifurcação do sistema entre e , que se manifesta por uma duplicação do período de oscilação.
(c) Repetem-se novamente os comandos das alíneas anteriores, agora com .
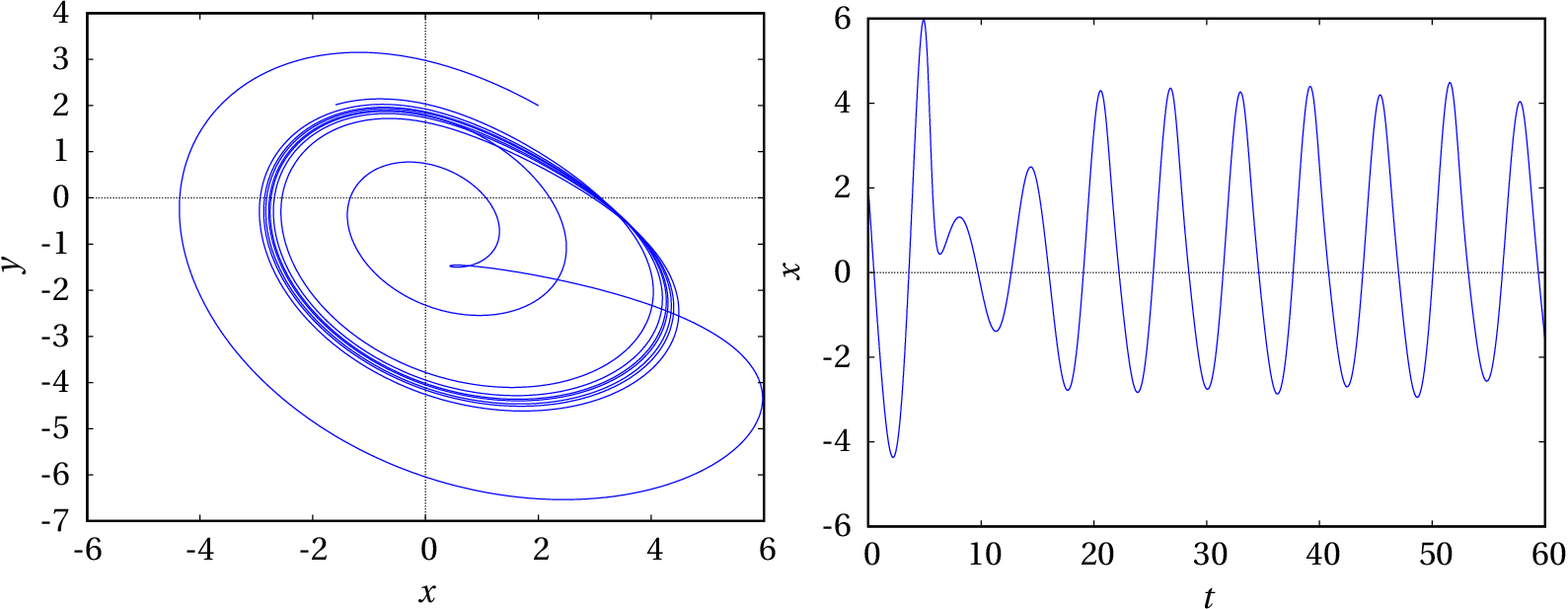
E deixa-se evoluir a solução durante outro intervalo .
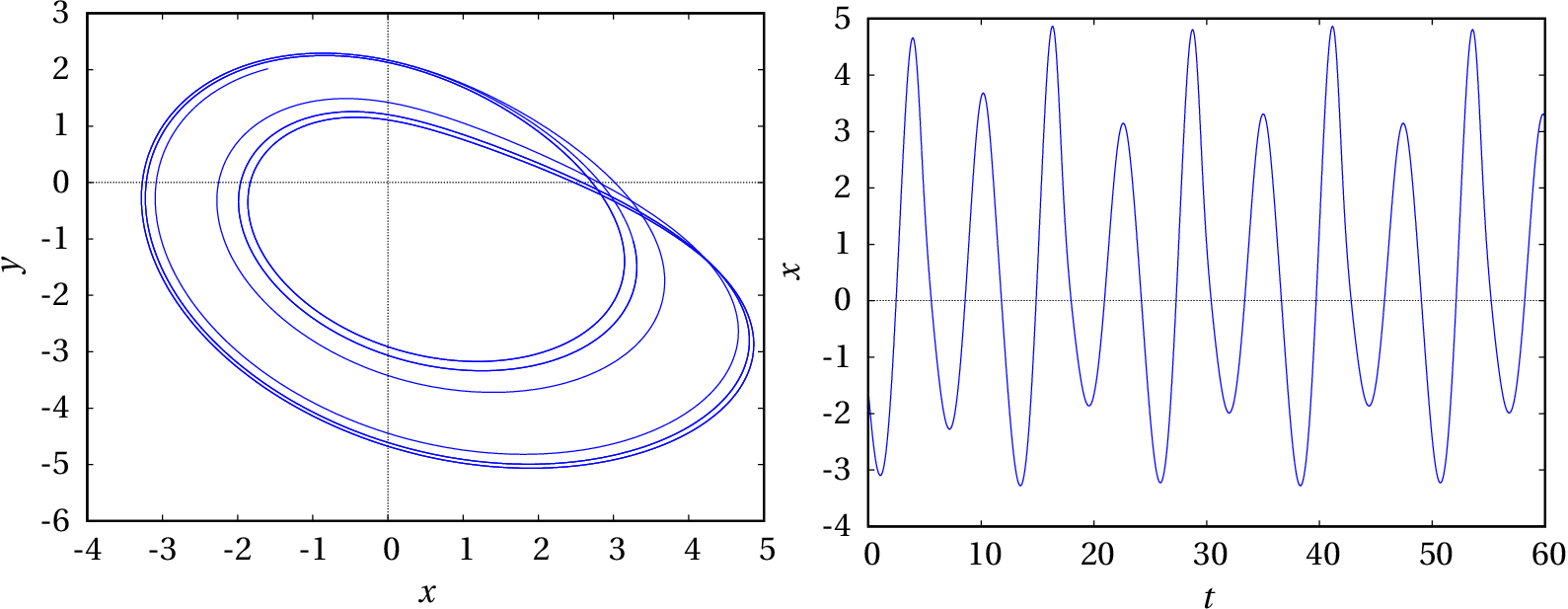
O gráfico no plano mostra que o sistema ainda não entrou no ciclo limite, porque a curva não é fechada. Deixaremos evoluir a solução durante mais um intervalo .
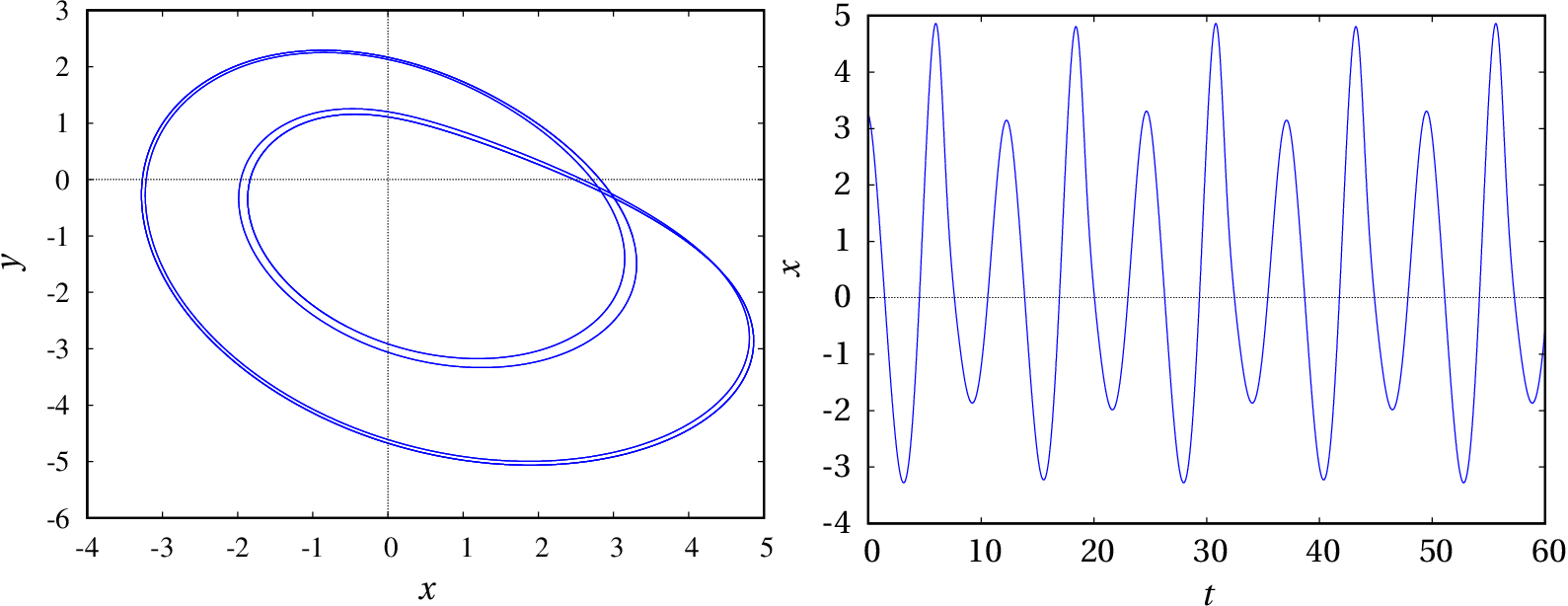
O sistema já entrou no ciclo limite atrativo que é agora de quarta ordem: há 4 máximos locais e 4 mínimos locais em cada oscilação e o ciclo dá quatro voltas no espaço de fase antes de se repetir. No gráfico de observam-se apenas 2 oscilações completas e o valor medido para o período é:
que é aproximadamente o dobro do período no ciclo de segunda ordem obtido com . Existe uma segunda bifurcação do sistema entre e que conduz a uma nova duplicação do período de oscilação.
(d) Repetem-se novamente os comandos das alíneas anteriores, agora com .
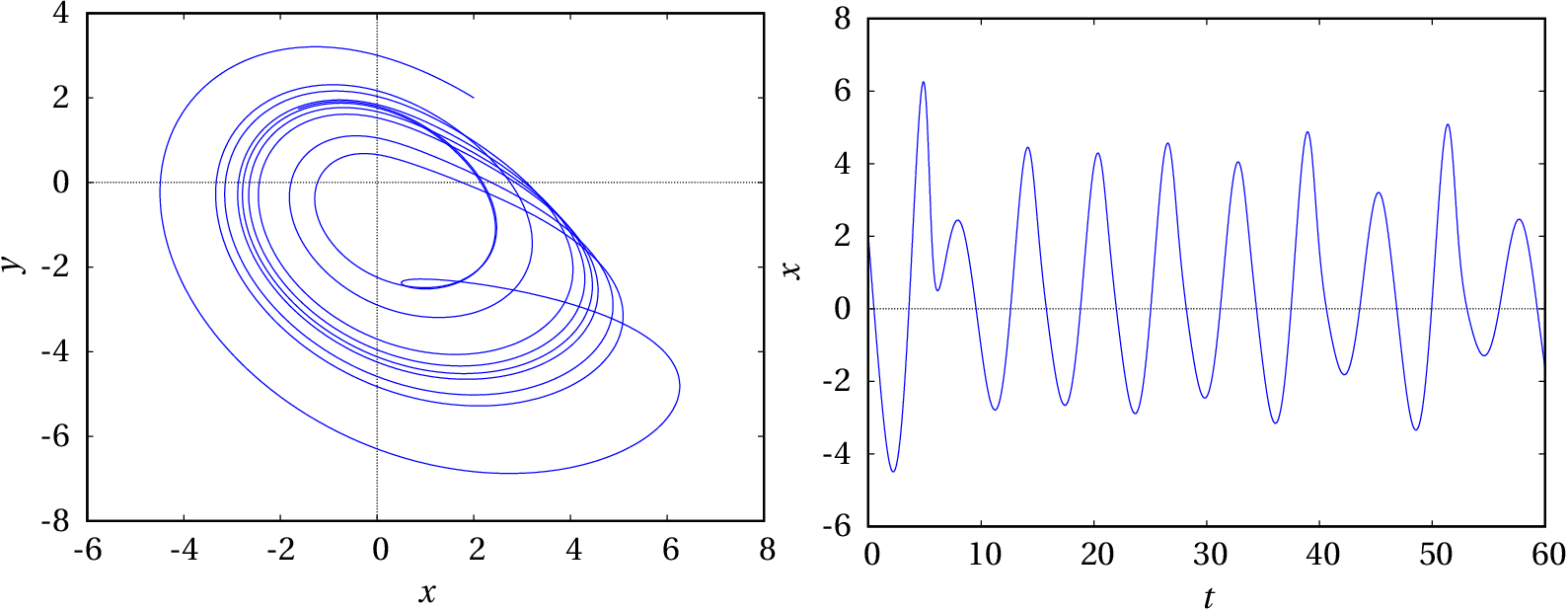
E deixa-se evoluir a solução durante outro intervalo .
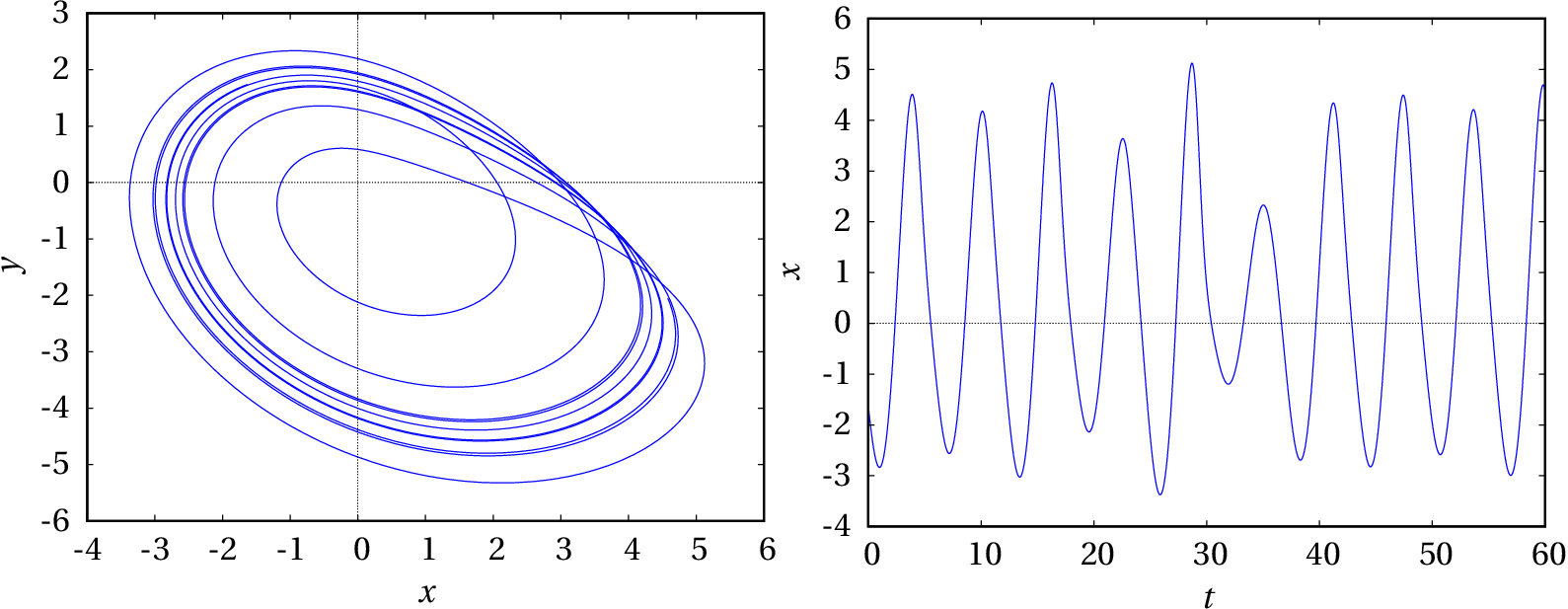
Continuando com mais intervalos observa-se que nunca se consegue reproduzir o mesmo resultado do intervalo anterior:
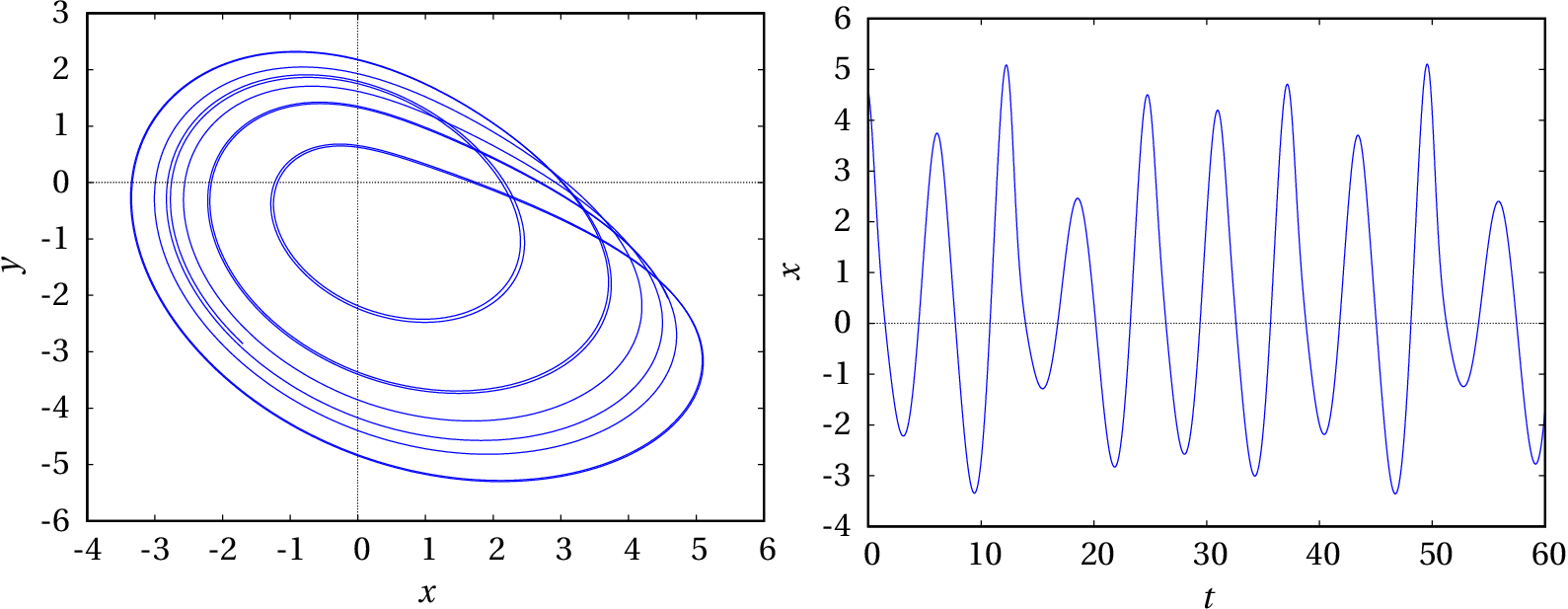
No aumento de de 0.375 para 0.398 houve infinitas bifurcações. O intervalo entre os valores de onde há novas bifurcações é cada vez menor, de forma que o período de oscilação aproxima-se de infinito. O sistema é caótico quando e os últimos dois gráficos mostram duas partes do ciclo limite, que é um atrator estranho.