A. Análise vetorial

A.1 Vetores e escalares

É importante distinguir entre escalares, por exemplo, energia, massa, carga, e vetores, por exemplo, velocidade, força, campo elétrico. Os escalares são representados apenas por um número, enquanto que para caraterizar um vetor é preciso saber o seu módulo (também chamado norma, intensidade ou magnitude), a sua direção e o seu sentido.

Para distinguir os vetores dos escalares usaremos uma seta por cima da variável que identifica o vetor, por exemplo, o vetor $\overrightarrow{a}$. O módulo (ou norma) desse vetor é um escalar positivo e será representado pela mesma letra, sem seta: $a$. Também é usada a notação $\left|\overrightarrow{a}\right|$ para o módulo de um vetor. A direção e o sentido do vetor $\overrightarrow{a}$ são definidos por um versor (vetor com módulo igual a 1), que representaremos colocando acento circunflexo por cima da letra, neste caso, $\hat{a}$. Um versor também é designado por vetor unitário. O vetor $\overrightarrow{a}$ pode então ser escrito da seguinte forma:

$$\overrightarrow{a}=a\hat{a}$$ (A.1)

Um versor não possui unidades (é uma grandeza adimensional), pelo que as unidades de $\overrightarrow{a}$ e de $a$ devem de ser as mesmas. Dado um vetor $\overrightarrow{a}$ não nulo, o seu versor pode ser obtido facilmente invertendo a expressão (A.1): $\hat{a}=\overrightarrow{a}/a$.

A soma de dois vetores, $\overrightarrow{a}+\overrightarrow{b}$, pode ser definida geometricamente pela lei do paralelogramo, a qual consiste em deslocar um dos vetores de forma a fazer coincidir o seu ponto inicial com o ponto final do primeiro, obtendo-se como resultado o vetor que vai desde o ponto inicial do primeiro vetor até o ponto final do segundo (figura A.1).

Figura A.1: Soma (esquerda) e subtração (direita) de dois vetores.

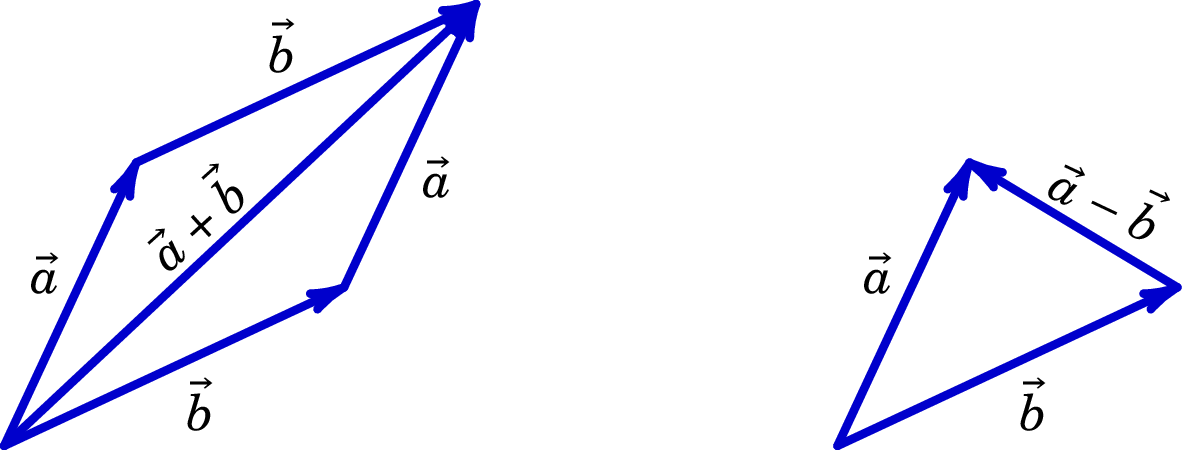
A soma de vetores satisfaz as propriedades comutativa e associativa:

$\overrightarrow{a}+\overrightarrow{b}$ $=\overrightarrow{b}+\overrightarrow{a}$

$(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}$ $=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})$

O vetor zero, $\overrightarrow{0}$, é o vetor em que o ponto inicial e final são o mesmo (módulo igual a zero). Todo vetor $\overrightarrow{a}$ tem um vetor simétrico, $-\overrightarrow{a}$, que somado a vetor $\overrightarrow{a}$ dá como resultado o vetor zero. O simétrico de um vetor $\overrightarrow{a}$ obtém-se trocando os pontos inicial e final, o que faz mudar o sentido mantendo o mesmo módulo e a mesma direção.

A subtração de dois vetores, $\overrightarrow{a}-\overrightarrow{b}$, é o vetor que vai desde o ponto final de $\overrightarrow{b}$ até o ponto final de $\overrightarrow{a}$, quando os dois vetores são colocados num ponto inicial comum, tal como mostra a figura A.1. Note que a subtração de dois vetores é igual à soma do primeiro vetor com o simétrico do segundo: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})$.

O produto $k\overrightarrow{a}$, entre um escalar $k$ e um vetor $\overrightarrow{a}$, é igual a outro vetor com a mesma direção de $\overrightarrow{a}$ mas com módulo igual a $|k|a$. O sentido de $k\overrightarrow{a}$ é o mesmo de $\overrightarrow{a}$, se $k$ for positivo, ou oposto se $k$ for negativo.

O ângulo entre dois vetores é definido como sendo o menor ângulo formado pelos vetores quando estes são colocados de modo a possuirem a mesma origem (ou ponto inicial), conforme a figura A.2.

Figura A.2: Ângulo entre dois vetores.

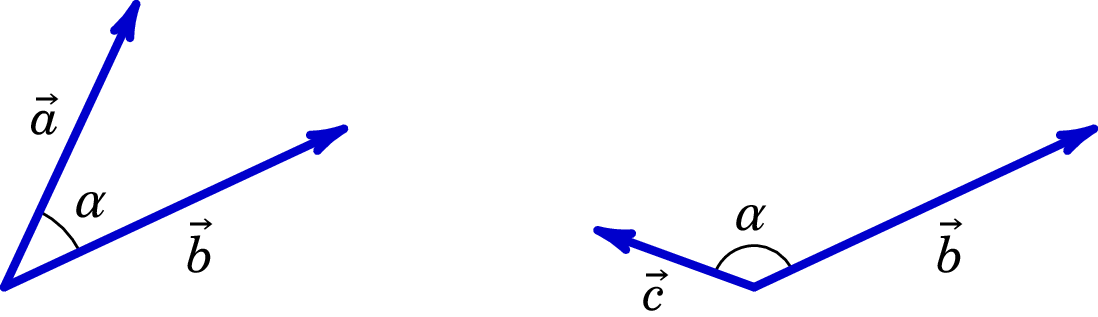
O ângulo $\alpha$ entre vetores encontra-se entre 0 e $\pi$. Quando os vetores possuem a mesma direção e o mesmo sentido (vetores paralelos) então $\alpha =0$, quando são perpendiculares $\alpha =\pi /2$ e para $\alpha =\pi$ os vetores possuem a mesma direção mas sentidos opostos (vetores anti-paralelos).

O produto escalar entre dois vetores é um escalar, o qual é igual ao produto dos seus módulos pelo cosseno do ângulo formado por eles.

$$\overrightarrow{a}\cdot \overrightarrow{b}=ab\cos \alpha$$ (A.2)

onde $\alpha$ é o ângulo formado pelos vetores. Por outras palavras, o produto escalar é igual ao produto da projeção de um dos vetores sobre o outro pelo módulo do segundo vetor, conforme a figura A.3.

Figura A.3: Produto escalar entre dois vetores.

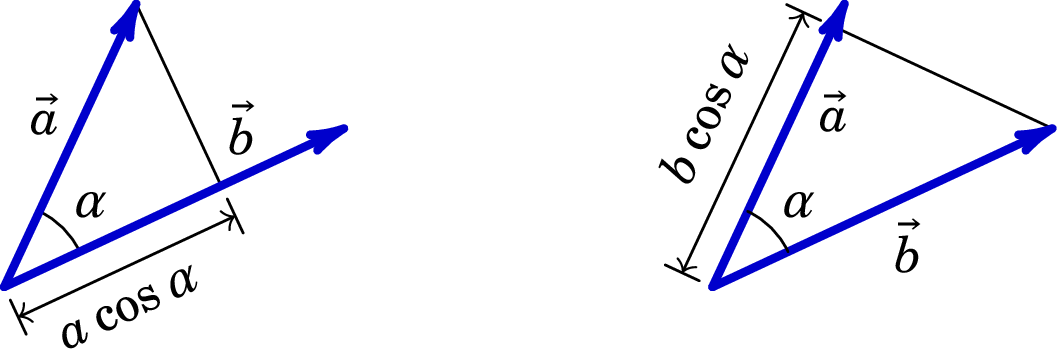
O produto escalar é máximo, nulo e mínimo quando os vetores são paralelos, perpendiculares e anti-paralelos, respetivamente.

O produto escalar satisfaz as propriedades comutativa e distributiva em relação à soma:

$\overrightarrow{a}\cdot \overrightarrow{b}$ $=\overrightarrow{b}\cdot \overrightarrow{a}$ (A.3)

$\overrightarrow{a}\cdot (\overrightarrow{b}+\overrightarrow{c})$ $=\overrightarrow{a}\cdot \overrightarrow{b}+\overrightarrow{a}\cdot \overrightarrow{c}$ (A.4)

O módulo de um vetor $\overrightarrow{a}$ pode ser obtido a partir do produto escalar do vetor com ele próprio:

$$a=\sqrt{\overrightarrow{a}\cdot \overrightarrow{a}}$$ (A.5)

O produto escalar é particularmente útil para se obter o ângulo $\alpha$ entre dois vetores $\overrightarrow{a}$ e $\overrightarrow{b}$ conhecidos. Através da expressão (A.2), temos então que:

$$\alpha =\arccos \left(\frac{\overrightarrow{a}\cdot \overrightarrow{b}}{ab}\right)$$ (A.6)

Um outro resultado útil é o obtido para o módulo da diferença entre dois vetores:

$${|\overrightarrow{a}-\overrightarrow{b}|}^2=(\overrightarrow{a}-\overrightarrow{b})\cdot (\overrightarrow{a}-\overrightarrow{b})=a^2+b^2-2ab\cos \alpha$$ (A.7)

onde $\alpha$ é o ângulo entre os dois vetores. Considerando o vector $\overrightarrow{c}=\overrightarrow{a}-\overrightarrow{b}$ (ver figura A.1), temos que:

$$c^2=a^2+b^2-2ab\cos \alpha$$ (A.8)

O resultado acima é conhecido como o teorema do cosseno, o qual é uma generalização do teorema de Pitágoras para qualquer tipo de triângulo. O teorema do cosseno afirma pois que o quadrado de um dos lados de um qualquer triângulo é igual à soma dos quadrados dos outros dois lados subtraída do dobro do produto desses dois lados pelo cosseno do ângulo formado por estes. Quando $\alpha =\pi /2$, obtemos o teorema de Pitágoras válido apenas para triângulos retângulos.

O produto vetorial entre dois vetores é um vetor com direção perpendicular a ambos, cujo sentido é dado pela regra da mão direita e de módulo igual ao produto dos módulos dos dois vetores pelo seno do ângulo entre eles. Do ponto de vista geométrico, o módulo do produto vetorial é igual à área do paralelogramo formado pelos vetores (ver figura A.4):

$$|\overrightarrow{a}\times \overrightarrow{b}|=ab\sin \alpha$$ (A.9)

O módulo do produto vetorial é nulo, máximo e nulo quando os vetores são paralelos, perpendiculares e anti-paralelos, respetivamente.

Figura A.4: Produto vetorial entre dois vetores.

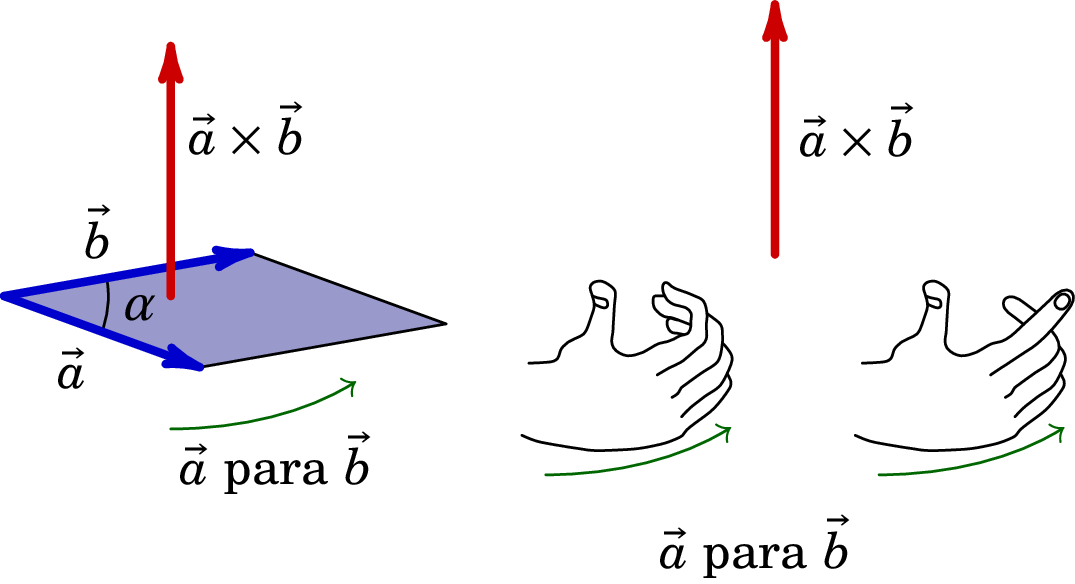
O produto vetorial é anti-comutativo e satisfaz a propriedade distributiva em relação à soma:

$\overrightarrow{a}\times \overrightarrow{b}$ $=-\overrightarrow{b}\times \overrightarrow{a}$ (A.10)

$\overrightarrow{a}\times (\overrightarrow{b}+\overrightarrow{c})$ $=\overrightarrow{a}\times \overrightarrow{b}+\overrightarrow{a}\times \overrightarrow{c}$ (A.11)

O produto escalar triplo entre três vetores é um escalar definido por:

$$(\overrightarrow{a}\times \overrightarrow{b})\cdot \overrightarrow{c}$$ (A.12)

e o seu módulo corresponde, do ponto de vista geométrico, ao volume do paralelepípedo gerado pelos três vetores conforme mostra a figura A.5.

Figura A.5: Produto escalar triplo entre três vetores.

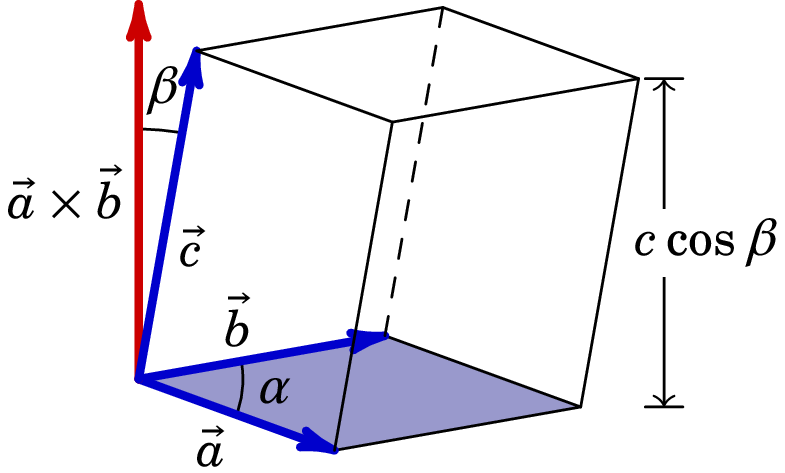
O produto escalar triplo satizfaz a seguinte propriedade:

$$(\overrightarrow{a}\times \overrightarrow{b})\cdot \overrightarrow{c}=(\overrightarrow{b}\times \overrightarrow{c})\cdot \overrightarrow{a}=(\overrightarrow{c}\times \overrightarrow{a})\cdot \overrightarrow{b}$$ (A.13)

O produto vetorial triplo entre três vetores é um vetor definido por $\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})$e satisfaz a seguinte propriedade:

$\overrightarrow{a}\times (\overrightarrow{b}\times \overrightarrow{c})$ $=(\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b}-(\overrightarrow{a}\cdot \overrightarrow{b})\overrightarrow{c}$ (A.14)

O produto escalar quádruplo, o qual envolve quatro vetores, é um escalar definido por $(\overrightarrow{a}\times \overrightarrow{b})\cdot (\overrightarrow{c}\times \overrightarrow{d})$ e obedece à seguinte propriedade:

$(\overrightarrow{a}\times \overrightarrow{b})\cdot (\overrightarrow{c}\times \overrightarrow{d})$ $=(\overrightarrow{a}\cdot \overrightarrow{c})(\overrightarrow{b}\cdot \overrightarrow{d})-(\overrightarrow{a}\cdot \overrightarrow{d})(\overrightarrow{b}\cdot \overrightarrow{c})$ (A.15)

A.2 Sistemas de coordenadas

Um sistema de coordenadas no espaço tridimensional consiste, em termos simples, em definir três coordenadas mutuamente independentes. Seja um sistema de coordenadas $e_1$, $e_2$ e $e_3$, as quais podem ser comprimentos, ângulos, ou outras grandezas geométricas. Um qualquer ponto P deste espaço é identificado pelas suas coordenadas, a saber, $\text{P}\equiv (e_1,e_2,e_3)$.

Em cada ponto do espaço, existem três versores ${\hat{e}}_1$, ${\hat{e}}_2$ e ${\hat{e}}_3$, os quais são tangentes à respetiva coordenada $e_1$, $e_2$ ou $e_3$ e que possuem o sentido segundo o qual a coordenada aumenta.

Vamos considerar apenas sistemas de coordenadas ortonormados dextrógiros. Isto significa que os versores de cada uma das coordenadas em cada ponto do espaço são sempre ortogonais (perpendiculares) entre si, possuem norma (módulo) igual à unidade e satisfazem a regra da mão direita.

A.2.1 Coordenadas cartesianas

O sistema de coordenadas cartesianas (também ditas retangulares) consiste em definir três eixos retilíneos $x$, $y$ e $z$ mutuamente perpendiculares. De modo a que todos os pontos do espaço estejam identificados pelas três coordenadas cartesianas, $\text{P}\equiv (x,y,z)$, e a que haja uma correspondência biunívoca (também dita bijetiva) entre pontos e coordenadas, as três coordenadas podem ter quaisquer valores reais.

Figura A.6: Sistema de coordenadas cartesianas e componentes de um vetor $\overrightarrow{a}$.

Os três versores cartesianos $\hat{ı}$, $\hat{ȷ}$ e $\hat{k}$ apontam nas direções desses três eixos, possuem o sentido do aumento da respetiva coordenada e são ortonormados, isto é, o produto escalar entre dois versores diferentes é zero e o produto escalar de cada versor consigo próprio é igual a 1. Os versores cartesianos satisfazem também a regra da mão direita, propriedade expressa pelos seguintes produtos vetoriais:

$$\hat{ı}\times \hat{ȷ}=\hat{k}\mathit{\hspace{1em}\hspace{1em}}\hat{ȷ}\times \hat{k}=\hat{ı}\mathit{\hspace{1em}\hspace{1em}}\hat{k}\times \hat{ı}=\hat{ȷ}$$ (A.16)

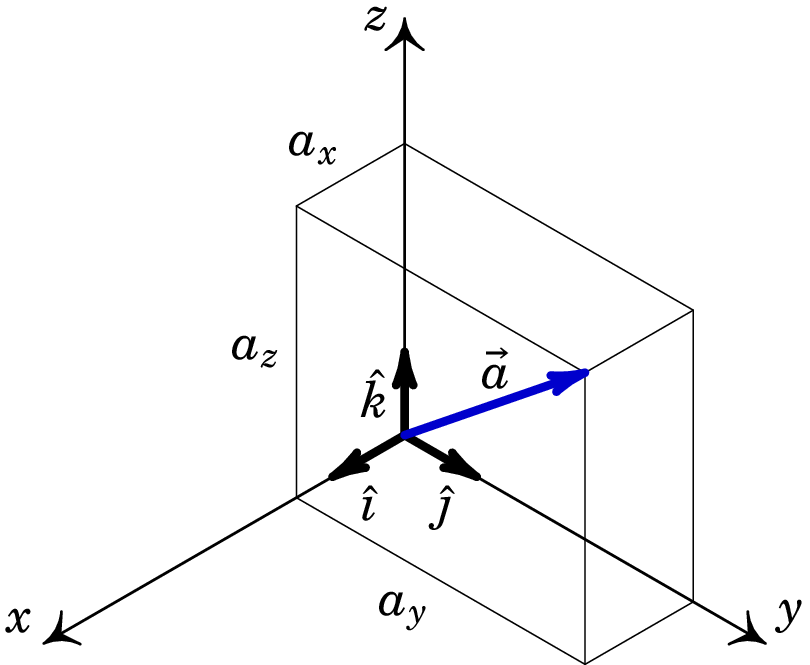
Os versores cartesianos são vetores constantes, i.e., são sempre iguais em qualquer ponto do espaço (ver figura A.6) e formam o que se denomina por base vetorial completa. Isto significa que qualquer vetor $\overrightarrow{a}$ deste espaço pode ser escrito como uma combinação linear dos versores da base, a saber,

$$\overrightarrow{a}=a_x\hat{ı}+a_y\hat{ȷ}+a_z\hat{k}$$ (A.17)

As três componentes cartesianas $a_x$, $a_y$ e $a_z$ de um vetor $\overrightarrow{a}$ são as três arestas do paralelepípedo obtido colocando os três versores $\hat{ı}$, $\hat{ȷ}$ e $\hat{k}$ no ponto inicial do vetor e projetando o ponto final até aos três planos $xy$, $xz$ e $yz$, tal como mostra a figura A.6. As componentes cartesianas do vetor $\overrightarrow{a}$ são dadas pois pelas suas projeções nos versores cartesianos, no ponto onde se encontra o vetor:

$$a_x=\overrightarrow{a}\cdot \hat{ı}\mathit{\hspace{1em}\hspace{1em}}{a}_y=\overrightarrow{a}\cdot \hat{ȷ}\mathit{\hspace{1em}\hspace{1em}}{a}_z=\overrightarrow{a}\cdot \hat{k}$$ (A.18)

É importante referir que, apesar de serem números, as componentes de um vetor não são grandezas escalares, uma vez que em geral são diferentes em diferentes sistemas de coordenadas, enquanto que uma grandeza escalar é sempre igual em todos eles — considera-se que é usado o mesmo sistema de unidades nos diferentes sistemas de coordenadas e que estes não possuem movimento relativo uns em relação aos outros.

Em coordenadas cartesianas, a soma ou subtração de dois vetores é feita somando ou subtraindo respetivamente as coordenadas dos vetores:

$$\overrightarrow{a}\pm \overrightarrow{b}=(a_x\pm b_x)\hat{ı}+(a_y\pm b_y)\hat{ȷ}+(a_z\pm b_z)\hat{k}$$ (A.19)

O produto escalar de vetores em coordenadas cartesianas é dado por:

$\overrightarrow{a}\cdot \overrightarrow{b}$ $=(a_x\hat{ı}+a_y\hat{ȷ}+a_z\hat{k})\cdot (b_x\hat{ı}+b_y\hat{ȷ}+b_z\hat{k})$

$=a_x{b}_x+a_y{b}_y+a_z{b}_z$ (A.20)

onde foram usadas as propriedades do produto escalar e a ortonormalização dos versores. Deste modo, o produto escalar obtém-se analiticamente multiplicando ordenadamente as componentes dos vetores e somando os resultados.

A equação (A.5) conduz à expressão do módulo de um vetor:

$$a=\sqrt{a_x^2+a_y^2+a_z^2}$$ (A.21)

a qual pode ser considerada uma extensão do teorema de Pitágoras a três dimensões.

O produto vetorial de dois vetores em coordenadas cartesianas tem a seguinte expressão em coordenadas cartesianas:

$\overrightarrow{a}\times \overrightarrow{b}$ $=(a_x\hat{ı}+a_y\hat{ȷ}+a_z\hat{k})\times (b_x\hat{ı}+b_y\hat{ȷ}+b_z\hat{k})$

$=(a_y{b}_z-a_z{b}_y)\hat{ı}+(a_z{b}_x-a_x{b}_z)\hat{ȷ}+(a_x{b}_y-a_y{b}_x)\hat{k}$ (A.22)

onde foram usadas as propriedades do produto vetorial e a propriedade dos versores obedecerem à regra da mão direita (expressão (A.16). O resultado da expressão (A.2.1) costuma ser escrito na forma de um determinante:

(A.23)

Define-se o vetor posição $\overrightarrow{r}$ de um ponto P no espaço como sendo o vetor que começa na origem do sistema de coordenadas e termina no ponto P. Em coordenadas cartesianas, o vetor posição é dado por:

$$\overrightarrow{r}=x\hat{ı}+y\hat{ȷ}+z\hat{k}$$ (A.24)

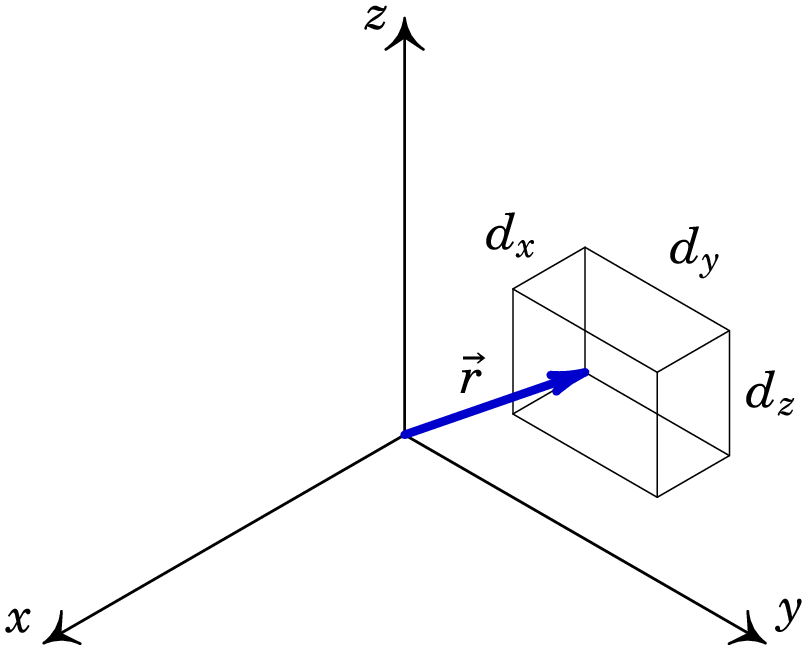
No cálculo de integrais de linha é necessário usar o denominado vetor deslocamento infinitesimal $\mathrm{d}\overrightarrow{r}$. Este vetor corresponde ao deslocamento infinitesimal vetorial de um ponto de vetor posição $\overrightarrow{r}$ para um ponto infinitesimalmente próximo cujo vetor de posição é $\overrightarrow{r}+\mathrm{d}\overrightarrow{r}$. O vetor posição depende das três coordenadas cartesianas: $\overrightarrow{r}(x,y,z)$, expressão (A.24). Usando a regra de diferenciação para uma função de várias variáveis aplicada à expressão (A.24), temos que:

$$\mathrm{d}\overrightarrow{r}=\frac{\partial \overrightarrow{r}}{\partial x}\mathrm{d}x+\frac{\partial \overrightarrow{r}}{\partial y}\mathrm{d}y+\frac{\partial \overrightarrow{r}}{\partial z}\mathrm{d}z$$ (A.25)

A partir da expressão (A.24) vemos que as três derivadas parciais de $\overrightarrow{r}$ são os três versores cartesianos e, como tal, o vetor deslocamento infinitesimal é:

$$\mathrm{d}\overrightarrow{r}=\mathrm{d}x\hat{ı}+\mathrm{d}y\hat{ȷ}+\mathrm{d}z\hat{k}$$ (A.26)

Os três termos na expressão (A.26) são designados por deslocamentos infinitesimais de arco (ou “elemento infinitesimal de linha” e ainda “elemento infinitesimal de percurso”). A figura A.7. mostra os três deslocamentos infinitesimais.

Figura A.7: Deslocamentos infinitesimais segundo as coordenadas cartesianas.

No cálculo de integrais de superfície é necessário usar o denominado vetor infinitesimal de área $\mathrm{d}\overrightarrow{A}$ correspondente à superfície em causa. O módulo deste vetor é o elemento infinitesimal de área $\mathrm{d}A$ e a sua direção é a direção normal à superfície:

$$\mathrm{d}\overrightarrow{A}=\mathrm{d}A\hat{n}$$ (A.27)

onde $\hat{n}$ é o versor normal (perpendicular) à superfície.

Em particular os três vetores infinitesimais de área paralelos aos três eixos coordenados têm a direção dos três versores cartesianos e módulo igual à área do retângulo definido pelos dois deslocamentos infinitesimais perpendiculares ao respetivo versor (faces do paralelepípedo na figura A.7):

$$\mathrm{d}{\overrightarrow{A}}_x=\mathrm{d}y\mathrm{d}z\hat{ı}\mathit{\hspace{1em}\hspace{1em}}\mathrm{d}{\overrightarrow{A}}_y=\mathrm{d}z\mathrm{d}x\hat{ȷ}\mathit{\hspace{1em}\hspace{1em}}\mathrm{d}{\overrightarrow{A}}_z=\mathrm{d}x\mathrm{d}y\hat{k}$$ (A.28)

onde os índices indicam a direção perpendicular à superfície.

Num integral de volume, o elemento infinitesimal de volume $\mathrm{d}v$ é o volume do paralelepípedo definido pelos deslocamentos infinitesimais segundo as três coordenadas (ver figura A.7):

$$\mathrm{d}v=\mathrm{d}x\mathrm{d}y\mathrm{d}z$$ (A.29)

Os deslocamentos infinitesimais $\mathrm{d}x$, $\mathrm{d}y$ e $\mathrm{d}z$ possuem unidades de comprimento e os versores não possuem unidades. Assim, os elementos infinitesimais $\mathrm{d}\overrightarrow{r}$, $\mathrm{d}A$ e $\mathrm{d}v$ possuem undidades de comprimento, de comprimento ao quadrado e comprimento ao cubo, respetivamente, como deve ser.

A.2.2 Coordenadas polares

Quando os vetores considerados estão todos no mesmo plano, basta usar dois eixos coordenados, habitualmente $x$ e $y$. O vetor posição de cada ponto do plano em coordenadas cartesianas terá então apenas duas componentes segundo $x$ e $y$:

$$\overrightarrow{r}=x\hat{ı}+y\hat{ȷ}$$ (A.30)

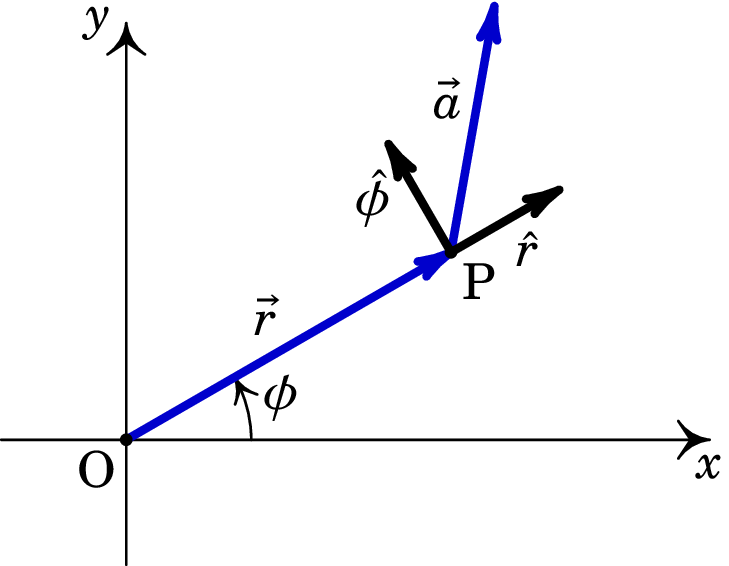
As coordenadas polares do ponto são ($r$, $\varphi$), onde a coordenada radial $r$ é o módulo do vetor posição $\overrightarrow{r}$ e a coordenada angular $\varphi$ é o ângulo que esse vetor faz com o semieixo positivo $x$ (figura A.8). De modo a que todos os pontos do espaço estejam identificados pelas duas coordenadas polares e que estas sejam únicas, a coordenada radial $r$ poderá ter qualquer valor real positivo ou zero e a coordenada angular $\varphi$ estará entre 0 e $2\pi$.

Figura A.8: Coordenadas polares.

As coordenadas cartesianas ($x$, $y$) de um ponto permitem calcular as suas coordenadas polares ($r$, $\varphi$) e vice versa, a partir das expressões:

$$\{\begin{array}{cc}r=\sqrt{x^2+y^2}\hfill & \\ \varphi ={\tan }^{-1}\left(\frac{y}{x}\right)\hfill & \end{array}\mathit{\hspace{1em}}\{\begin{array}{cc}x=r\cos \varphi \hfill & \\ y=r\sin \varphi \hfill & \end{array}$$ (A.31)

Os dois versores do sistema de coordenadas polares são o versor radial $\hat{r}$, que aponta na direção em que $r$ aumenta, e o versor angular $\hat{\varphi }$, também na direção em que $\varphi$ aumenta (ver figura A.8). Estes versores são ortonormados: o produto escalar entre eles é nulo e o produto escalar de cada um deles consigo próprio é igual a 1.

Ao contrário do que acontece com os versores cartesianos, estes versores são em geral diferentes em diferentes pontos do espaço. Nomeadamente, os versores radial e angular dependem da coordenada angular $\varphi$:

$$\{\begin{array}{cc}\hat{r}=\cos \varphi \hat{ı}+\sin \varphi \hat{ȷ}\hfill & \\ \hat{\varphi }=-\sin \varphi \hat{ı}+\cos \varphi \hat{ȷ}\hfill & \end{array}$$ (A.32)

Um vetor genérico $\overrightarrow{a}$ em coordenadas polares escreve-se como:

$$\overrightarrow{a}=a_r\hat{r}+a_{\varphi }\hat{\varphi }$$ (A.33)

onde as componentes polares $a_r$ e $a_{\varphi }$ são as projeções de $\overrightarrow{a}$ nos versores $\hat{r}$ e $\hat{\theta }$, no ponto onde se encontra o vetor (figura A.8):

$$a_r=\overrightarrow{a}\cdot \hat{r}\mathit{\hspace{1em}\hspace{1em}}{a}_{\varphi }=\overrightarrow{a}\cdot \hat{\varphi }$$ (A.34)

Observe-se que quando se desloca um dado vetor de um ponto para um outro ponto no espaço, o vetor permance o mesmo. Assim, enquanto que as componentes cartesianas desse vetor permanecem inalteradas, as suas componentes polares são, em geral, diferentes em diferentes pontos do espaço.

O vetor posição em coordenadas polares é dado por:

$\overrightarrow{r}$ $=r\hat{r}$ (A.35)

$=r\cos \varphi \hat{ı}+r\sin \varphi \hat{ȷ}$ (A.36)

Note que o vetor posição em coordenadas polares não possui componente angular, i.e., não possui componente segundo o versor $\hat{\varphi }$. O vetor deslocamento infinitesimal em coordenadas polares do ponto de vetor posição $\overrightarrow{r}$ é dado por:

$\mathrm{d}\overrightarrow{r}$ $={\displaystyle \frac{\partial \overrightarrow{r}}{\partial r}}\mathrm{d}r+{\displaystyle \frac{\partial \overrightarrow{r}}{\partial \varphi }}\mathrm{d}\varphi$

$=\mathrm{d}r\hat{r}+r\mathrm{d}\varphi \hat{\varphi }$ (A.37)

Tal como se procedeu em coordenadas cartesianas, o vetor deslocamento infinitesimal em coordenadas polares, expressão (A.2.2), pode ser obtido intuitivamente considerando os deslocamentos infinitesimais segundo as coordenadas polares: $\mathrm{d}r$ e $r\mathrm{d}\varphi$, conforme a figura A.9. Note que o comprimento de arco de uma circunferência é dado pelo produto do seu raio $r$ pelo ângulo $\mathrm{d}\varphi$ percorrido sobre a circunferência. O vetor deslocamento infinitesimal $\mathrm{d}\overrightarrow{r}$ é dado pela soma dos deslocamentos infinitesimais segundo os versores polares, e obtemos a expressão (A.2.2).

Figura A.9: Deslocamentos infinitesimais segundo as coordenadas polares.

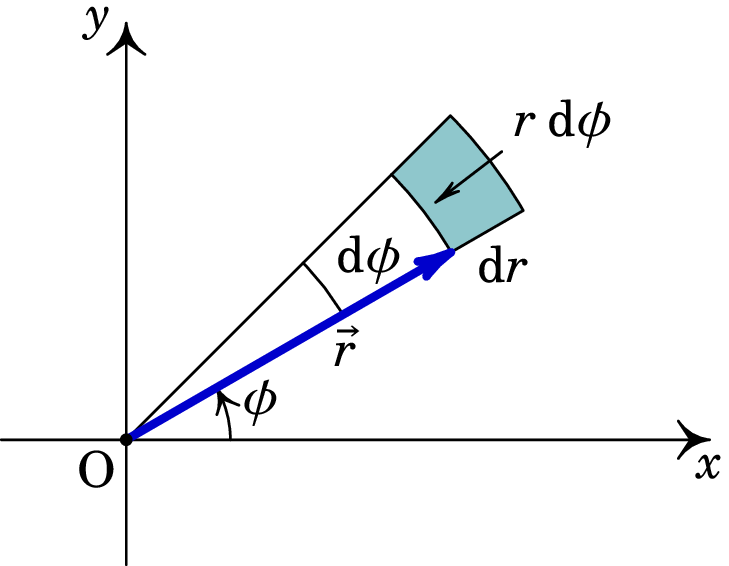
No limite de deslocamentos infinitesimais, o segmento de coroa circular representado na figura A.9, tende para um retângulo. Assim, o elemento infinitesimal de área é igual à área do retângulo definido pelos dois deslocamentos infinitesimais nas direções $\hat{r}$ e $\hat{\varphi }$:

$$\mathrm{d}A=r\mathrm{d}\varphi \mathrm{d}r$$ (A.38)

Os deslocamentos infinitesimais $\mathrm{d}r$ e $r\mathrm{d}\varphi$ possuem unidades de comprimento (os ângulos não possuem dimensão) e os versores não possuem unidades. Assim, os elementos infinitesimais $\mathrm{d}\overrightarrow{r}$ e $\mathrm{d}A$ possuem unidades de comprimento e de comprimento ao quadrado, respetivamente, como deve ser.

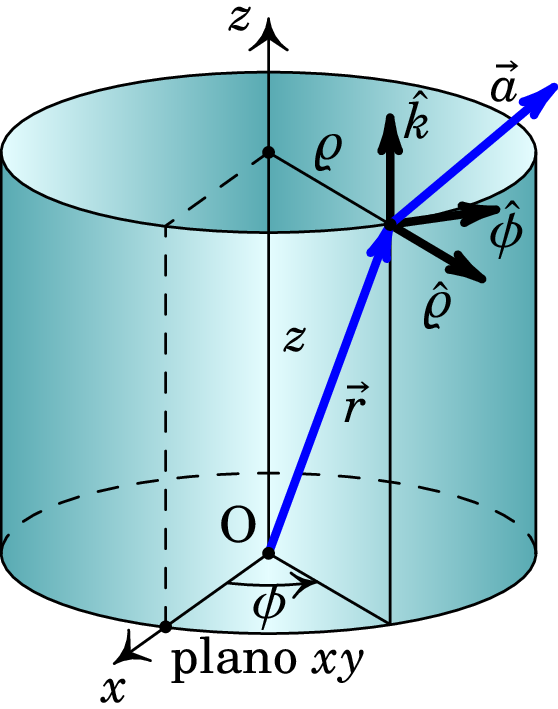
A.2.3 Coordenadas cilíndricas

As coordenadas cilíndricas de um ponto são ($\varrho$, $\varphi$, $z$), em que $\varrho$ é a distância até o eixo $z$ (coordenada radial cilíndrica), $\varphi$ o ângulo que a projeção dessa distância no plano $xy$ faz com o semieixo positivo $x$ (coordenada azimutal) e $z$ a coordenada cartesiana (ver figura A.10). De modo a que todos os pontos do espaço estejam identificados pelas três coordenadas cilíndricas e que estas sejam únicas, a coordenada $z$ deverá ser qualquer número real, a coordenada radial $\varrho$ qualquer número real positivo ou nulo e a coordenada azimutal $\varphi$ um número real entre 0 e $2\pi$.

Figura A.10: Coordenadas cilíndricas.

A relação entre as coordenadas cartesianas ($x$, $y$, $z$) e cilíndricas ($\varrho$, $\varphi$, $z$) de um ponto é a seguinte (a coordenada $z$ é igual nos dois sistemas):

$$\{\begin{array}{cc}\varrho =\sqrt{x^2+y^2}\hfill & \\ \varphi ={\tan }^{-1}\left(\frac{y}{x}\right)\hfill & \end{array}\mathit{\hspace{1em}}\{\begin{array}{cc}x=\varrho \cos \varphi \hfill & \\ y=\varrho \sin \varphi \hfill & \end{array}$$ (A.39)

Os versores nas direções em que as três coordenadas aumentam são $\hat{\varrho }$, $\hat{\varphi }$ e $\hat{k}$ (ver figura A.10). Estes versores são ortonormados: o produto escalar entre dois versores diferentes é nulo e o produto escalar de cada versor consigo próprio é igual a 1, e satisfazem a regra da mão direita:

$$\hat{\varrho }\times \hat{\varphi }=\hat{k}\mathit{\hspace{1em}\hspace{1em}}\hat{\varphi }\times \hat{k}=\hat{\varrho }\mathit{\hspace{1em}\hspace{1em}}\hat{k}\times \hat{\varrho }=\hat{\varphi }$$ (A.40)

Ao contrário dos versores cartesianos, os versores cilíndricos são em geral diferentes em diferentes pontos do espaço. Enquanto que o versor $\hat{k}$ é constante, os versores radial e azimutal dependem da coordenada azimutal $\varphi$:

$$\{\begin{array}{cc}\hat{\varrho }=\cos \varphi \hat{ı}+\sin \varphi \hat{ȷ}\hfill & \\ \hat{\varphi }=-\sin \varphi \hat{ı}+\cos \varphi \hat{ȷ}\hfill & \end{array}$$ (A.41)

Um vetor genérico $\overrightarrow{a}$ em coordenadas cilíndricas escreve-se como:

$$\overrightarrow{a}=a_{\varrho }\hat{\varrho }+a_{\varphi }\hat{\varphi }+a_z\hat{k}$$ (A.42)

onde as componentes cilíndricas $a_{\varrho }$, $a_{\varphi }$ e $a_z$ são as suas projeções de $\overrightarrow{a}$ nos correspondentes versores no ponto onde se encontra o vetor (figura A.10):

$$a_{\varrho }=\overrightarrow{a}\cdot \hat{\varrho }\mathit{\hspace{1em}\hspace{1em}}{a}_{\varphi }=\overrightarrow{a}\cdot \hat{\varphi }\mathit{\hspace{1em}\hspace{1em}}{a}_z=\overrightarrow{a}\cdot \hat{k}$$ (A.43)

Observe-se que quando se desloca um dado vetor de um ponto para um outro ponto no espaço, o vetor permanece o mesmo. Assim, enquanto que as componentes cartesianas desse vetor permanecem inalteradas, as suas componentes cilíndricas são, em geral, diferentes em diferentes pontos do espaço.

O vetor posição em coordenadas cilíndricas é:

$\overrightarrow{r}$ $=\varrho \hat{\varrho }+z\hat{k}$ (A.44)

$=\varrho \cos \varphi \hat{ı}+\varrho \sin \varphi \hat{ȷ}+z\hat{k}$ (A.45)

Note que o vetor posição em coordenadas cilíndricas não possui componente azimutal, i.e., não possui componente segundo o versor $\hat{\varphi }$. O vetor deslocamento infinitesimal do ponto de vetor posição $\overrightarrow{r}$ é dado por:

$\mathrm{d}\overrightarrow{r}$ $={\displaystyle \frac{\partial \overrightarrow{r}}{\partial \varrho }}\mathrm{d}\varrho +{\displaystyle \frac{\partial \overrightarrow{r}}{\partial \varphi }}\mathrm{d}\varphi +{\displaystyle \frac{\partial \overrightarrow{r}}{\partial z}}\mathrm{d}z$

$=\mathrm{d}\varrho \hat{\varrho }+\varrho \mathrm{d}\varphi \hat{\varphi }+\mathrm{d}z\hat{k}$ (A.46)

O vetor deslocamento infinitesimal em coordenadas cilíndricas, expressão (A.2.3), pode ser obtido intuitivamente considerando os deslocamentos infinitesimais segundo as coordenadas cilíndricas: $\mathrm{d}\varrho$, $\varrho \mathrm{d}\varphi$ e $\mathrm{d}z$, conforme a figura A.11. Note que o comprimento de arco de uma circunferência é dado pelo produto do seu raio $\varrho$ pelo ângulo $\mathrm{d}\varphi$ percorrido sobre a circunferência. O vetor deslocamento infinitesimal $\mathrm{d}\overrightarrow{r}$ é então igual à soma dos deslocamentos infinitesimais segundo os versores cilíndricos, e obtemos a expressão (A.2.3).

Figura A.11: Deslocamentos infinitesimais segundo as coordenadas cilíndricas.

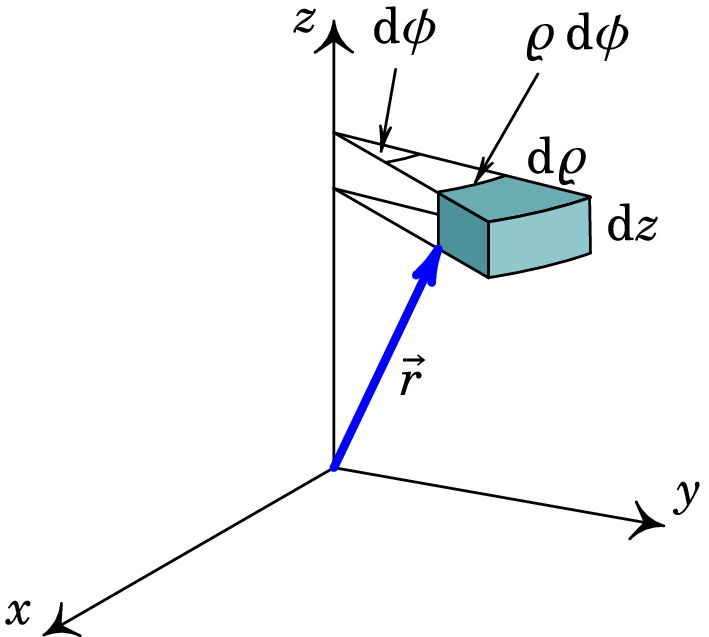
O elemento infinitesimal de área, numa superfície perpendicular ao versor $\hat{\varrho }$, i.e., numa superfície com $\varrho$ constante, é igual à área do retângulo definido pelos dois deslocamentos infinitesimais nas direções perpendiculares a $\hat{\varrho }$, ou seja, nas direções $\hat{\varphi }$ e $\hat{k}$. Seguindo este procedimento, os elementos infinitesimais de área em superfícies com $\varrho$, $\varphi$ e $z$ constantes são, respetivamente, dados por:

$$\mathrm{d}{\overrightarrow{A}}_{\varrho }=\varrho \mathrm{d}\varphi \mathrm{d}z\hat{\varrho }\mathit{\hspace{1em}\hspace{1em}}\mathrm{d}{\overrightarrow{A}}_{\varphi }=\mathrm{d}\varrho \mathrm{d}z\hat{\varphi }\mathit{\hspace{1em}\hspace{1em}}\mathrm{d}{\overrightarrow{A}}_z=\varrho \mathrm{d}\varrho \mathrm{d}\varphi \hat{k}$$ (A.47)

No limite de deslocamentos infinitesimais, o volume infinitesimal representado na figura A.11 tende para um paralelepípedo. Assim, o elemento infinitesimal de volume é o volume do paralelepípedo definido pelos deslocamentos infinitesimais segundo as três coordenadas:

$$\mathrm{d}v=\varrho \mathrm{d}\varrho \mathrm{d}\varphi \mathrm{d}z$$ (A.48)

Os deslocamentos infinitesimais $\mathrm{d}\varrho$, $\varrho \mathrm{d}\varphi$ e $dz$, possuem unidades de comprimento (os ângulos não possuem dimensão) e os versores não possuem unidades. Assim, os elementos infinitesimais $\mathrm{d}\overrightarrow{r}$, $\mathrm{d}A$ e $\mathrm{d}v$ possuem undidades de comprimento, de comprimento ao quadrado e comprimento ao cubo, respetivamente, como deve ser.

As coordenadas polares são um caso particular das coordenadas cilíndricas quando $z=0$, sendo que neste caso $\varrho \equiv r$.

A.2.4 Coordenadas esféricas

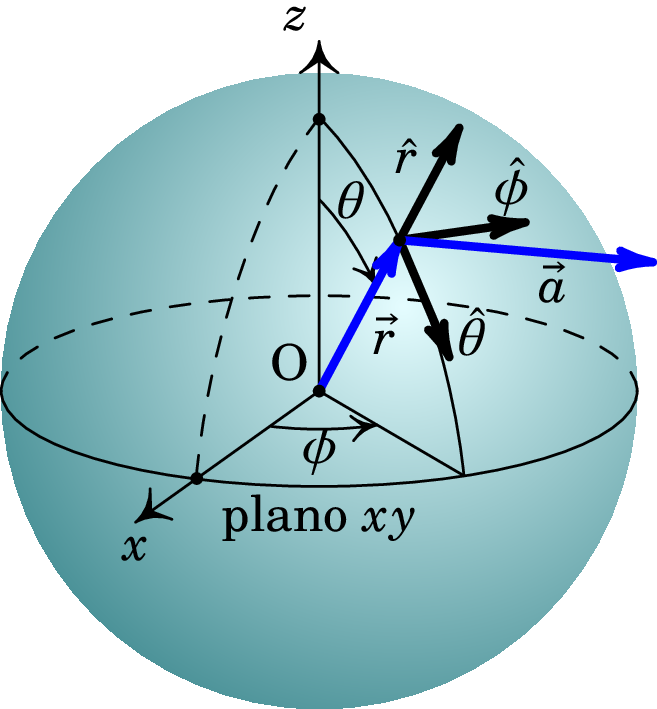
As coordenadas esféricas de um ponto são ($r$, $\theta$, $\varphi$), em que a coordenada radial $r$ é a distância até a origem, a coordenada zenital $\theta$ é o ângulo que o segmento entre a origem e o ponto faz com o semieixo positivo $z$ e a coordenada azimutal $\varphi$ é o ângulo que a projeção desse segmento no plano $xy$ faz com o semieixo positivo $x$ (ver figura A.12). De modo a que todos os pontos do espaço estejam identificados pelas três coordenadas esféricas e que estas sejam únicas, a coordenada radial $r$ deverá ser um número real positivo ou zero, a coordenada zenital $\theta$ deverá ser um número real entre 0 e $\pi$ e a coordenada azimutal $\varphi$ deverá ser um número real entre 0 e $2\pi$.

Figura A.12: Coordenadas esféricas.

A relação entre as coordenadas cartesianas ($x$, $y$, $z$) e esféricas ($r$, $\theta$, $\varphi$) de um ponto é a seguinte:

$$\{\begin{array}{cc}r=\sqrt{x^2+y^2+z^2}\hfill & \\ \theta ={\tan }^{-1}\left(\sqrt{x^2+y^2}/z\right)\hfill & \\ \varphi ={\tan }^{-1}\left(y/x\right)\hfill & \end{array}\mathit{\hspace{1em}}\{\begin{array}{cc}x=r\sin \theta \cos \varphi \hfill & \\ y=r\sin \theta \sin \varphi \hfill & \\ z=r\cos \theta \hfill & \end{array}$$ (A.49)

Os versores nas direções em que as três coordenadas aumentam, são $\hat{r}$, $\hat{\theta }$ e $\hat{\varphi }$ (figura A.12). Estes versores são ortonormados: o produto escalar entre dois versores diferentes é nulo e o produto escalar de cada versor consigo próprio é igual a 1, e satisfazem a regra da mão direita:

$$\hat{r}\times \hat{\theta }=\hat{\varphi }\mathit{\hspace{1em}\hspace{1em}}\hat{\theta }\times \hat{k}=\hat{r}\mathit{\hspace{1em}\hspace{1em}}\hat{\varphi }\times \hat{r}=\hat{\theta }$$ (A.50)

Os versores esféricos são em geral diferentes em diferentes pontos do espaço, nomeadamente, o versor $\hat{\varphi }$ depende do ângulo $\varphi$ e os versores $\hat{r}$ e $\hat{\theta }$ dependem dos ângulos $\varphi$ e $\theta$:

$$\{\begin{array}{cc}\hat{r}=\sin \theta \cos \varphi \hat{ı}+\sin \theta \sin \varphi \hat{ȷ}+\cos \theta \hat{k}\hfill & \\ \hat{\theta }=\cos \theta \cos \varphi \hat{ı}+\cos \theta \sin \varphi \hat{ȷ}-\sin \theta \hat{k}\hfill & \\ \hat{\varphi }=-\sin \varphi \hat{ı}+\cos \varphi \hat{ȷ}\hfill & \end{array}$$ (A.51)

Um vetor genérico $\overrightarrow{a}$ em coordenadas esféricas escreve-se como:

$$\overrightarrow{a}=a_r\hat{r}+a_{\theta }\hat{\theta }+a_{\varphi }\hat{\varphi }$$ (A.52)

onde as componentes esféricas $a_r$, $a_{\theta }$ e $a_{\varphi }$ são as projeções do vetor $\overrightarrow{a}$ nos correspondentes versores no ponto onde se encontra o vetor (figura A.12):

$$a_r=\overrightarrow{a}\cdot \hat{r}\mathit{\hspace{1em}\hspace{1em}}{a}_{\theta }=\overrightarrow{a}\cdot \hat{\theta }\mathit{\hspace{1em}\hspace{1em}}{a}_{\varphi }=\overrightarrow{a}\cdot \hat{\varphi }$$ (A.53)

Observe-se que quando se desloca um dado vetor de um ponto para um outro ponto no espaço, o vetor permance o mesmo. Assim, enquanto que as componentes cartesianas desse vetor permanecem inalteradas, as suas componentes esféricas são, em geral, diferentes em diferentes pontos do espaço.

O vetor posição em coordenadas esféricas é:

$\overrightarrow{r}$ $=r\hat{r}$ (A.54)

$=r\sin \theta \cos \varphi \hat{ı}+r\sin \theta \sin \varphi \hat{ȷ}+r\cos \theta \hat{k}$ (A.55)

Note que o vetor posição em coordenadas esféricas possui apenas componente radial esférica, i.e., não possui componentes segundo os versores zential $\hat{\theta }$ e azimutal $\hat{\varphi }$. O vetor deslocamento infinitesimal do ponto de vetor posição $\overrightarrow{r}$ é dado por:

$\mathrm{d}\overrightarrow{r}$ $={\displaystyle \frac{\partial \overrightarrow{r}}{\partial r}}\mathrm{d}r+{\displaystyle \frac{\partial \overrightarrow{r}}{\partial \theta }}\mathrm{d}\theta +{\displaystyle \frac{\partial \overrightarrow{r}}{\partial \varphi }}\mathrm{d}\varphi$

$=\mathrm{d}r\hat{r}+r\mathrm{d}\theta \hat{\theta }+r\sin \theta \mathrm{d}\varphi \hat{\varphi }$ (A.56)

A expressão (A.2.4) do vetor deslocamento infinitesimal em coordenadas esféricas pode ser obtida intuitivamente considerando os deslocamentos infinitesimais segundo as coordenadas esféricas: $\mathrm{d}r$, $r\mathrm{d}\theta$ e $r\sin \theta \mathrm{d}\varphi$, conforme a figura A.13, sendo que o lado esquerdo da figura mostra apenas os dois arcos devidos aos aumentos infinitesimais dos dois ângulos $\theta$ e $\varphi$, e o lado direito mostra o volume delimitado pelos três deslocamentos infinitesimais. Note que o comprimento de arco ao longo da coordenada $\theta$ é dado pelo produto do seu raio $r$ pelo ângulo $\mathrm{d}\theta$ percorrido e o comprimento de arco ao longo da coordenada $\varphi$ é dado pelo produto do seu raio $r\sin \theta$ pelo ângulo $\mathrm{d}\varphi$ percorrido. O vetor deslocamento infinitesimal $\mathrm{d}\overrightarrow{r}$ é igual à soma dos deslocamentos infinitesimais segundo os versores esféricos, e obtemos a expressão (A.2.4).

Figura A.13: Deslocamentos infinitesimais segundo as coordenadas esféricas.

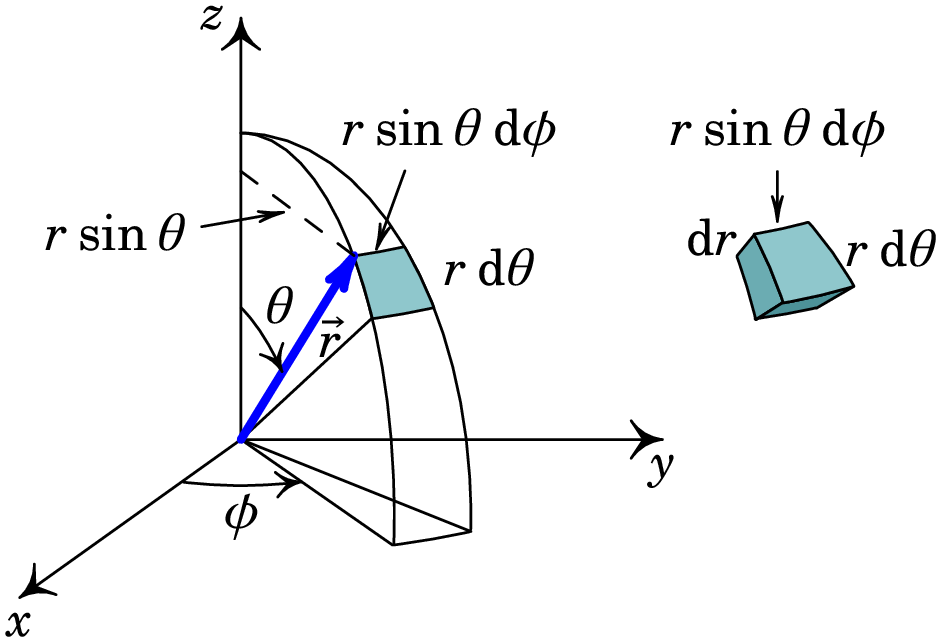
O elemento infinitesimal de área, numa superfície perpendicular ao versor $\hat{r}$, i.e., numa superfície com $r$ constante, é igual à área do retângulo definido pelos dois deslocamentos infinitesimais nas direções perpendiculares a $\hat{r}$, ou seja, nas direções $\hat{\theta }$ e $\hat{\varphi }$. Seguindo este procedimento, os elementos infinitesimais de área, em superfícies com $r$, $\theta$ ou $\varphi$ constantes, são, respetivamente, dados por:

$\mathrm{d}{\overrightarrow{A}}_r$ $=r^2\sin \theta \mathrm{d}\theta \mathrm{d}\varphi \hat{r}$ (A.57)

$\mathrm{d}{\overrightarrow{A}}_{\theta }$ $=r\sin \theta \mathrm{d}r\mathrm{d}\varphi \hat{\theta }$ (A.58)

$\mathrm{d}{\overrightarrow{A}}_{\varphi }$ $=r\mathrm{d}r\mathrm{d}\theta \hat{\varphi }$ (A.59)

No limite de deslocamentos infinitesimais, o volume infinitesimal representado na figura A.13 tende para um paralelepípedo. Assim, o elemento infinitesimal de volume é o volume do paralelepípedo definido pelos deslocamentos infinitesimais segundo as três coordenadas:

$$\mathrm{d}v=r^2\sin \theta \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi$$ (A.60)

Os deslocamentos infinitesimais esféricos $\mathrm{d}r$, $r\mathrm{d}\theta$ e $r\sin \theta \mathrm{d}\varphi$ possuem unidades de comprimento (os ângulos não possuem dimensão) e os versores não possuem unidades. Assim, os elementos infinitesimais $\mathrm{d}\overrightarrow{r}$, $\mathrm{d}A$ e $\mathrm{d}v$ possuem undidades de comprimento, de comprimento ao quadrado e comprimento ao cubo, respetivamente, como deve ser.

As coordenadas polares são um caso particular das coordenadas esféricas quando $\theta =\pi /2$.

A.3 Campos vetoriais e escalares

Um campo escalar é uma função $f(\overrightarrow{r})$ que associa um escalar a cada ponto do espaço; por exemplo, a temperatura ou a pressão em diferentes pontos da atmosfera. Em coordenadas cartesianas, o campo escalar $f$ é dado explicitamente por: $f(\overrightarrow{r})=f(x,y,z)$.

Um campo vetorial $\overrightarrow{u}(\overrightarrow{r})$ associa um vetor a cada ponto do espaço; por exemplo, a velocidade do ar em diferentes pontos da atmosfera. O campo vetorial $\overrightarrow{u}(\overrightarrow{r})$ são realmente três funções (componentes) do espaço, contudo cada uma destas funções não é um campo escalar, já que estas são, em geral, diferentes em diferentes sistemas de coordenadas. Por exemplo, em coordenadas cartesianas, o campo vetorial $\overrightarrow{u}(\overrightarrow{r})$ é dado explicitamente por:

$$\overrightarrow{u}(\overrightarrow{r})=u_x(x,y,z)\hat{ı}+u_y(x,y,z)\hat{ȷ}+u_z(x,y,z)\hat{k}$$ (A.61)

onde as funções $u_x$, $u_y$ e $u_z$ são as componentes do campo $\overrightarrow{u}$. Já em coordenadas esféricas as componentes do mesmo campo vetorial $\overrightarrow{u}$ são outras três funções diferentes:

$$\overrightarrow{u}(\overrightarrow{r})=u_r(r,\theta ,\varphi )\hat{r}+u_{\theta }(r,\theta ,\varphi )\hat{\theta }+u_{\varphi }(r,\theta ,\varphi )\hat{\varphi }$$ (A.62)

Em coordenadas cartesianas, derivar um campo vetorial em função de uma variável consiste em derivar cada uma das componentes. Em outros sistemas de coordenadas, os próprios versores do sistema de coordenadas dependem das coordenadas e, como tal, é preciso derivar cada produto de uma das componentes vezes um versor, tendo em conta que o versor também é uma função.

A.3.1 Gradiente

O operador vetorial nabla em coordenadas cartesianas é definido por:

$$\overrightarrow{\nabla }=\frac{\partial }{\partial x}\hat{ı}+\frac{\partial }{\partial y}\hat{ȷ}+\frac{\partial }{\partial z}\hat{k}$$ (A.63)

A aplicação do operador nabla a um campo escalar $f(\overrightarrow{r})=f(x,y,z)$ tem como resultado um campo vetorial designado por gradiente de $f$. Em coordenadas cartesianas, o gradiente é dado por:

$$\overrightarrow{\nabla }f=\frac{\partial f}{\partial x}\hat{ı}+\frac{\partial f}{\partial y}\hat{ȷ}+\frac{\partial f}{\partial z}\hat{k}$$ (A.64)

Note que o campo vetorial obtido pela expressão (A.64) é, como qualquer campo vetorial, um vetor cujas componentes e versores são função de cada ponto $(x,y,z)$ do espaço.

A derivada direcional de um campo escalar $f(x,y,z)$ na direção de um versor $\hat{e}$ é definida como o seguinte limite:

$${\mathrm{D}}_{\hat{e}}f(\overrightarrow{r})=\underset{\mathrm{\Delta }s\to 0}{lim}\frac{f(\overrightarrow{r}+\mathrm{\Delta }s\hat{e})-f(\overrightarrow{r})}{\mathrm{\Delta }s}=\overrightarrow{\nabla }f\cdot \hat{e}$$ (A.65)

isto é, a derivada de $f$ na direção dum versor $\hat{e}$ é igual à projeção do gradiente de $f$ na direção de $\hat{e}$. Como tal, o gradiente $\overrightarrow{\nabla }f$ aponta sempre na direção de maior variação de $f$ (ver figura A.14). As superfícies de nível de um campo escalar $f$ no espaço tridimensional são as superfícies onde o campo é constante. No caso do campo existir no espaço bidimensional as superfícies de nível são denominadas por curvas de nível. Nas direções perpendiculares ao gradiente $\overrightarrow{\nabla }f$, o valor do campo $f$ não muda, pelo que as curvas/superfícies de nível de um campo escalar são sempre perpendiculares ao seu gradiente.

Figura A.14: A função $f(x,y)=\sin x\sin y$, à esquerda, e o seu gradiente que é um campo vetorial no plano $xy$, representado à direita.

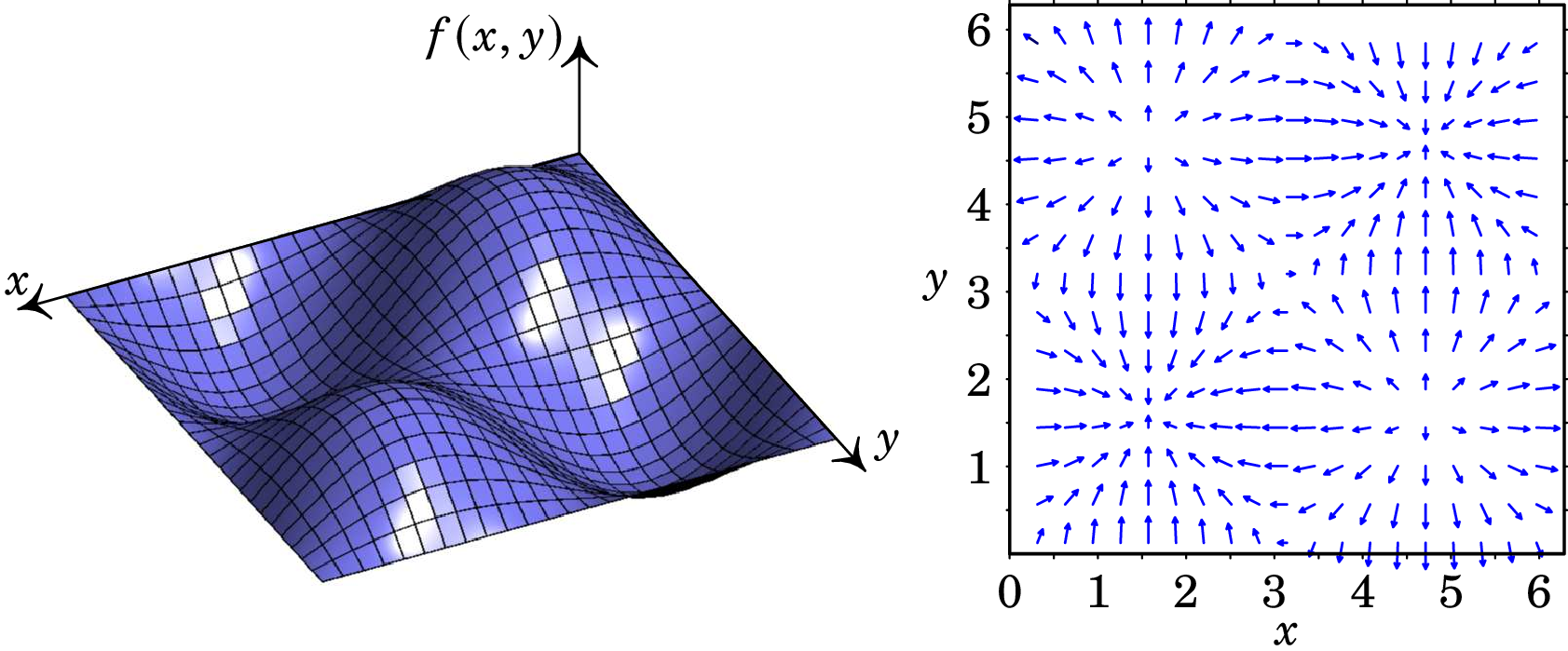
Em particular, as três derivadas parciais

$$\frac{\partial f}{\partial x}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}\frac{\partial f}{\partial y}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}\frac{\partial f}{\partial z}$$

são as derivadas de $f$ nas direções dos três eixos cartesianos, iguais às componentes do gradiente nas direções dos três versores cartesianos. Generalizando este resultado para outros sistemas de coordenadas, a componente do gradiente na direção de cada um dos versores desse sistema é o aumento da função $f$ dividido pelo comprimento do vetor deslocamento infinitesimal nessa direção.

Em coordenadas cilíndricas, usando os deslocamentos infinitesimais na equação (A.2.3), conclui-se que o gradiente é

$$\overrightarrow{\nabla }f=\frac{\partial f}{\partial \varrho }\hat{\varrho }+\frac{1}{\varrho }\frac{\partial f}{\partial \varphi }\hat{\varphi }+\frac{\partial f}{\partial z}\hat{k}$$ (A.66)

Em coordenadas esféricas, os deslocamentos infinitesimais na equação (A.2.4) conduzem à expressão

$$\overrightarrow{\nabla }f=\frac{\partial f}{\partial r}\hat{r}+\frac{1}{r}\frac{\partial f}{\partial \theta }\hat{\theta }+\frac{1}{r\sin \theta }\frac{\partial f}{\partial \varphi }\hat{\varphi }$$ (A.67)

A.3.2 Divergência

Em coordenadas cartesianas, a divergência de um campo vetorial $\overrightarrow{u}(x,y,z)$ é um campo escalar dado pela seguinte expressão:

$$\overrightarrow{\nabla }\cdot \overrightarrow{u}=\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}+\frac{\partial u_z}{\partial z}$$ (A.68)

Note que o campo escalar obtido pela expressão (A.68) é, como qualquer campo escalar, uma função de cada ponto $(x,y,z)$ do espaço.

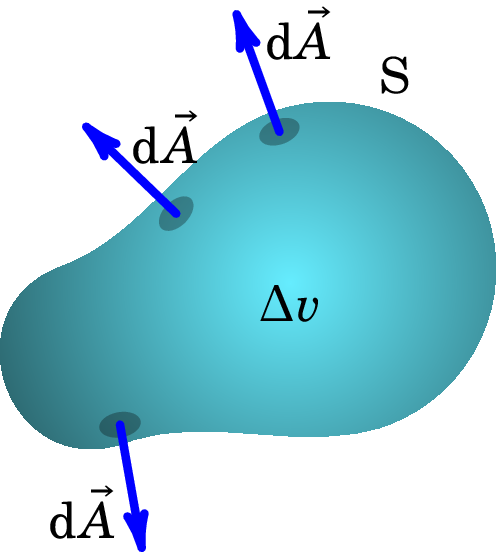
A definição geral da divergência, independente do sistema de coordenadas, é dada através do integral de superfície do campo vetorial $\overrightarrow{u}$ sobre a superfície S (fechada) que delimita um volume $\mathrm{\Delta }v$, englobando o ponto $(x,y,z)$ onde se calcula a divergência, dividida por esse volume e no limite em que o volume se aproxima de zero:

$$\overrightarrow{\nabla }\cdot \overrightarrow{u}=\underset{\mathrm{\Delta }v\to 0}{lim}\frac{1}{\mathrm{\Delta }v}{∯}_{\mathrm{S}}\overrightarrow{u}\cdot d\overrightarrow{A}$$ (A.69)

onde $\mathrm{d}\overrightarrow{A}$ é vetor infinitesimal de área, normal à superfície fechada S, o qual para uma superfície fechada aponta sempre para fora desta, conforme a figura A.15. A superfície S é denominada por fronteira do volume $\mathrm{\Delta }v$.

Figura A.15: Volume $\mathrm{\Delta }v$ com fronteira S e vetor infinitesimal de área $\mathrm{d}\overrightarrow{A}$ em várias partes de S.

A definição geral (A.69) da divergência usa-se para encontrar a expressão da divergência em outros sistemas de coordenadas. Em coordenadas cilíndricas:

$$\overrightarrow{\nabla }\cdot \overrightarrow{u}=\frac{1}{\varrho }\frac{\partial (\varrho u_{\varrho })}{\partial \varrho }+\frac{1}{\varrho }\frac{\partial u_{\varphi }}{\partial \varphi }+\frac{\partial u_z}{\partial z}$$ (A.70)

onde $u_{\varrho }=\overrightarrow{u}\cdot \hat{\varrho }$, $u_{\varphi }=\overrightarrow{u}\cdot \hat{\varphi }$ e $u_z=\overrightarrow{u}\cdot \hat{k}$ são as componentes cilíndricas do campo $\overrightarrow{u}$.

Em coordenadas esféricas, as três componentes do campo $\overrightarrow{u}$ são $u_r=\overrightarrow{u}\cdot \hat{r}$, $u_{\theta }=\overrightarrow{u}\cdot \hat{\theta }$ e $u_{\varphi }=\overrightarrow{u}\cdot \hat{\varphi }$ e a divergência é:

$$\overrightarrow{\nabla }\cdot \overrightarrow{u}=\frac{1}{r^2}\frac{\partial (r^2{u}_r)}{\partial r}+\frac{1}{r\sin \theta }\frac{\partial (u_{\theta }\sin \theta )}{\partial \theta }+\frac{1}{r\sin \theta }\frac{\partial u_{\varphi }}{\partial \varphi }$$ (A.71)

A expressão (A.69) conduz à seguinte equação, chamada teorema da divergência,

$${∯}_{\mathrm{S}}\overrightarrow{u}\cdot d\overrightarrow{A}={\iiint }_{\mathrm{R}}\overrightarrow{\nabla }\cdot \overrightarrow{u}dv$$ (A.72)

o qual é válido para qualquer campo vetorial $\overrightarrow{u}$ contínuo em qualquer região R do espaço (i.e., um volume finito) delimitada pela sua superfície S (fechada).

A.3.3 Rotacional

Em coordenadas cartesianas, o rotacional de um campo vetorial $\overrightarrow{u}(x,y,z)$ é um outro campo vetorial definido pela relação:

$$\overrightarrow{\nabla }\times \overrightarrow{u}=\left(\frac{\partial u_z}{\partial y}-\frac{\partial u_y}{\partial z}\right)\hat{ı}+\left(\frac{\partial u_x}{\partial z}-\frac{\partial u_z}{\partial x}\right)\hat{ȷ}+\left(\frac{\partial u_y}{\partial x}-\frac{\partial u_x}{\partial y}\right)\hat{k}$$ (A.73)

que costuma ser escrito também como o determinante:

(A.74)

Note que o campo vetorial obtido pela expressão (A.73) é, como qualquer campo vetorial, um vetor cujas componentes e versores são função de cada ponto $(x,y,z)$ do espaço.

Uma definição geral do rotacional, independente do sistema de coordenadas, é obtida considerando uma pequena superfície plana S, com área $\mathrm{\Delta }A$, contendo o ponto $(x,y,z)$ onde se calcula o rotacional, cuja fronteira é uma curva fechada C como a que aparece na figura A.16. Deve-se escolher um sentido de circulação para percorrer a curva C, fronteira da superfície S, e define-se o versor $\hat{n}$ normal à superfície S, segundo a regra da mão direita em relação ao sentido de circulação escolhido: rodando os dedos indicador, médio, anular e pequeno nesse sentido, o dedo polegar aponta no sentido do versor normal $\hat{n}$. Uma curva fechada com um sentido de circulação definido designa-se por curva fechada orientada. Ver figura A.16.

Figura A.16: Superfície plana S com fronteira orientada C, versor normal $\hat{n}$ no sentido da regra da mão direita e de área $\mathrm{\Delta }A$.

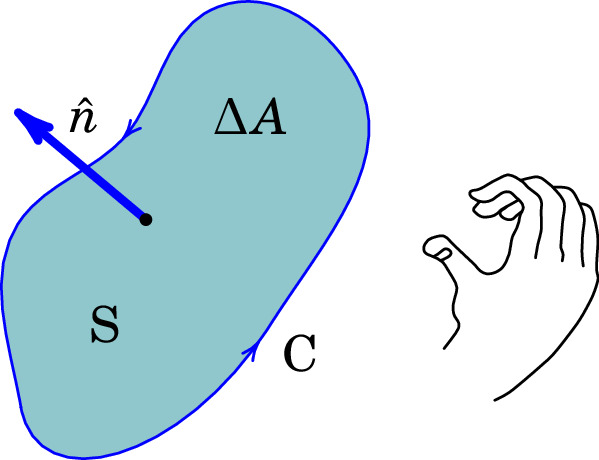
A componente do rotacional $\overrightarrow{\nabla }\times \overrightarrow{u}$ na direção de $\hat{n}$ é igual ao limite do integral de linha de $\overrightarrow{u}$ ao longo da curva fechada C e no sentido escolhido, dividido pela área $\mathrm{\Delta }A$ da superfície S, no limite quando essa área se aproxima de zero:

$$(\overrightarrow{\nabla }\times \overrightarrow{u})\cdot \hat{n}=\underset{\mathrm{\Delta }A\to 0}{lim}\frac{1}{\mathrm{\Delta }A}{\oint }_{\mathrm{C}}\overrightarrow{u}\cdot d\overrightarrow{r}$$ (A.75)

Em coordenadas cilíndricas, o rotacional do campo vetorial $\overrightarrow{u}$, de componentes cilíndricas $u_{\varrho }$, $u_{\varphi }$ e $u_z$ é igual a

$$\overrightarrow{\nabla }\times \overrightarrow{u}=\left(\frac{1}{\varrho }\frac{\partial u_z}{\partial \varphi }-\frac{\partial u_{\varphi }}{\partial z}\right)\hat{\varrho }+\left(\frac{\partial u_{\varrho }}{\partial z}-\frac{\partial u_z}{\partial \varrho }\right)\hat{\varphi }+\frac{1}{\varrho }\left(\frac{\partial (\varrho u_{\varphi })}{\partial \varrho }-\frac{\partial u_{\varrho }}{\partial \varphi }\right)\hat{k}$$ (A.76)

Em coordenadas esféricas, as componentes do campo vetorial $\overrightarrow{u}$ são $u_r$, $u_{\theta }$ e $u_{\varphi }$, e o seu rotacional é

$\overrightarrow{\nabla }\times \overrightarrow{u}$ $={\displaystyle \frac{1}{r\sin \theta }}\left({\displaystyle \frac{\partial (u_{\varphi }\sin \theta )}{\partial \theta }}-{\displaystyle \frac{\partial u_{\theta }}{\partial \varphi }}\right)\hat{r}+\left({\displaystyle \frac{1}{r\sin \theta }}{\displaystyle \frac{\partial u_r}{\partial \varphi }}-{\displaystyle \frac{1}{r}}{\displaystyle \frac{\partial (r{u}_{\varphi })}{\partial r}}\right)\hat{\theta }$

$+{\displaystyle \frac{1}{r}}\left({\displaystyle \frac{\partial (r{u}_{\theta })}{\partial r}}-{\displaystyle \frac{\partial u_r}{\partial \theta }}\right)\hat{\varphi }$ (A.77)

Qualquer campo vetorial $\overrightarrow{u}$ contínuo verifica o teorema de Stokes, em qualquer superfície simples S, com fronteira numa curva C:

$${\oint }_{\mathrm{C}}\overrightarrow{u}\cdot d\overrightarrow{r}={\iint }_{\mathrm{S}}(\overrightarrow{\nabla }\times \overrightarrow{u})\cdot d\overrightarrow{A}$$ (A.78)

onde o integral de linha é feito no sentido da regra da mão direita segundo a direção do vetor infinitesimal de área $\mathrm{d}\overrightarrow{A}$, dado pela expressão (A.27).

A.3.4 Laplaciano

O operador laplaciano em coordenadas cartesianas é definido por

$${\nabla }^2=\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}+\frac{{\partial }^2}{\partial z^2}$$ (A.79)

o qual que é um operador escalar. A aplicação de laplaciano a um campo escalar dá outro campo escalar definido pela expressão

$${\nabla }^{2}f=\frac{{\partial }^{2}f}{\partial x^2}+\frac{{\partial }^{2}f}{\partial y^2}+\frac{{\partial }^{2}f}{\partial z^2}$$ (A.80)

O laplaciano pode também ser aplicado a um campo vetorial $\overrightarrow{u}=u_x\hat{ı}+u_y\hat{ȷ}+u_z\hat{k}$, dando como resultado outro campo vetorial:

$${\nabla }^2\overrightarrow{u}=\frac{{\partial }^2{u}_x}{\partial x^2}\hat{ı}+\frac{{\partial }^2{u}_y}{\partial y^2}\hat{ȷ}+\frac{{\partial }^2{u}_z}{\partial z^2}\hat{k}$$ (A.81)

Em outros sistemas de coordenadas, o laplaciano pode ser obtido calculando o produto escalar do operador nabla consigo próprio. Em coordenadas cilíndricas o resultado é,

$${\nabla }^{2}f=\frac{1}{\varrho }\frac{\partial }{\partial \varrho }\left(\varrho \frac{\partial f}{\partial \varrho }\right)+\frac{1}{{\varrho }^2}\frac{{\partial }^{2}f}{\partial {\varphi }^2}+\frac{{\partial }^{2}f}{\partial z^2}$$ (A.82)

E em coordenadas esféricas,

$${\nabla }^{2}f=\frac{1}{r}\frac{{\partial }^2(rf)}{\partial r^2}+\frac{1}{r^2\sin \theta }\frac{\partial }{\partial \theta }\left(\sin \theta \frac{\partial f}{\partial \theta }\right)+\frac{1}{r^2{\sin }^2\theta }\frac{{\partial }^{2}f}{\partial {\varphi }^2}$$ (A.83)

Estas duas últimas expressões também são válidas para um campo vetorial $\overrightarrow{u}$ em vez do campo escalar $f$.

A.3.5 Propriedades dos operadores vetoriais

O gradiente, a divergência e o rotacional são operadores lineares. A seguir mostram-se algumas identidades importantes, válidas para quaisquer campos escalares contínuos $f$ e $g$, e quaisquer campos vetoriais contínuos $\overrightarrow{u}$ e $\overrightarrow{v}$.

$$\overrightarrow{\nabla }\times (\overrightarrow{\nabla }f)=\overrightarrow{0}$$ (A.84)

$$\overrightarrow{\nabla }\cdot (\overrightarrow{\nabla }\times \overrightarrow{u})=0$$ (A.85)

$${\nabla }^2(fg)=f{\nabla }^{2}g+2(\overrightarrow{\nabla }f\cdot \overrightarrow{\nabla }g)+g{\nabla }^{2}f$$ (A.86)

$$\overrightarrow{\nabla }\cdot (\overrightarrow{\nabla }f)={\nabla }^{2}f$$ (A.87)

$$\overrightarrow{\nabla }\cdot (f\overrightarrow{u})=\overrightarrow{\nabla }f\cdot \overrightarrow{u}+f\overrightarrow{\nabla }\cdot \overrightarrow{u}$$ (A.88)

$$\overrightarrow{\nabla }\cdot (f\overrightarrow{\nabla }g)=\overrightarrow{\nabla }f\cdot \overrightarrow{\nabla }g+f{\nabla }^{2}g$$ (A.89)

$$\overrightarrow{\nabla }\times (\overrightarrow{\nabla }\times \overrightarrow{u})=\overrightarrow{\nabla }(\overrightarrow{\nabla }\cdot \overrightarrow{u})-{\nabla }^2\overrightarrow{u}$$ (A.90)

$$\overrightarrow{\nabla }\cdot (\overrightarrow{u}\times \overrightarrow{v})=\overrightarrow{v}\cdot (\overrightarrow{\nabla }\times \overrightarrow{u})-\overrightarrow{u}\cdot (\overrightarrow{\nabla }\times \overrightarrow{v})$$ (A.91)

$$\overrightarrow{\nabla }\times (\overrightarrow{u}\times \overrightarrow{v})=\overrightarrow{u}(\overrightarrow{\nabla }\cdot \overrightarrow{v})-\overrightarrow{v}(\overrightarrow{\nabla }\cdot \overrightarrow{u})+(\overrightarrow{v}\cdot \overrightarrow{\nabla })\overrightarrow{u}-(\overrightarrow{u}\cdot \overrightarrow{\nabla })\overrightarrow{v}$$ (A.92)