12. Luz

Jaime E. Villate e Luís Miguel Martelo

(25 de janeiro de 2025)

Heinrich Rudolph Hertz (1857–1894)

A pesar de que o valor previsto por Maxwell para a velocidade das ondas eletromagnéticas concordava com o valor da velocidade da luz no vácuo, já conhecido na época, enquanto não fosse possível produzir e detetar ondas eletromagnéticas no laboratório as ondas eletromagnéticas eram apenas uma hipótese teórica. Em 1887 Hertz consegiu, pela primeira vez na história, produzir ondas eletromagnéticas a partir de um circuito elétrico; ficou assim estabelecida a existência das ondas eletromagnéticas, reforçando a ideia de que a luz é uma onda eletromagnética e não partículas, como na teoria corpuscular da luz. A ironia do destino é que na mesma experiência em que Hertz produz pela primeira vez uma onda eletromagnética, descobre acidentalmente o efeito fotoelétrico, que só poderá ser explicado corretamente por Einstein, 18 anos mais tarde, admitindo que a luz são partículas e não ondas.

12.1 História das teorias da luz

Terminaremos este livro falando sobre o papel importante que o eletromagnetismo teve na consolidação da física clássica e, ao mesmo tempo, expondo as suas fraquezas que levaram ao surgimento da física moderna. Desde a época de Newton, dois séculos antes de Maxwell, existiam duas teorias diferentes acerca da luz, propostas por Isaac Newton (1642–1727) e o seu contemporâneo Christian Huygens (1629–1695).

12.1.1 Teoria corpuscular da luz

Na teoria corpuscular de Newton, a luz é formada por partículas. A luz propaga-se em linha reta — raios de luz — o qual é compatível com as trajetórias retas das partículas em movimento livre. Newton explicou muitos outros fenómenos com a sua teoria corpuscular.

Quando um raio de luz passa de um meio 1 para outro meio 2 como no lado esquerdo da figura 12.1, parte da luz é refletida no meio 1 e outra parte é refratada, passando para meio 2. Observa-se que o ângulo que o raio incidente faz com a perpendicular à superfície de separação entre os dois meios, $\theta_{1}$ no lado esquerdo da figura 12.1, é igual ao ângulo que o raio refletido faz com essa perpendicular, enquanto que o ângulo que o raio refratado faz com a perpendicular, $\theta_{2}$ , é diferente.

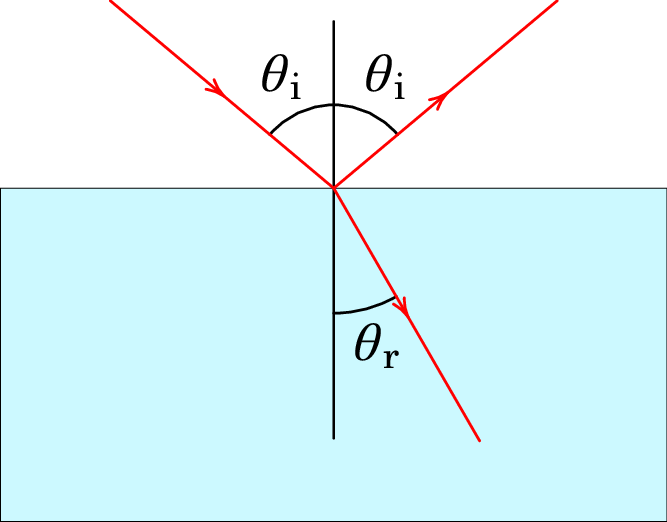
Reflexão e refração de um raio de luz que passa de um meio
para outro. — Figura 12.1: Reflexão e refração de um raio de luz que passa de um meio para outro.

Mudando o ângulo $\theta_{1}$ , observa-se que a relação,

\dfrac{\sin\theta_{1}}{\sin\theta_{2}}=n_{21}

(12.1)

permanece constante, e é designada de índice de refração relativo, neste caso do meio 2 relativo ao meio 1. O índice de refracção entre dois meios onde a luz pode propagar-se é uma constante caraterística desses meios.

Se um segundo raio de luz fosse enviado no meio 2 em direção da interface entre os meios (lado direito da figura 12.1), com ângulo de incidência $\theta_{2}$ igual ao ângulo de refração do primeiro raio, novamente observa-se a igualdade entre os ângulos de incidência e de reflexão e o ângulo de refração será o mesmo ângulo de incidência, $\theta_{1}$ , do primeiro raio. Isto é, o índice de refração do meio 1 relativo ao meio 2, $n_{12}$ , é o inverso do índice de refração do meio 2 relativo ao meio 1, $n_{21}$ .

A reflexão e a refração da luz explicam-se no modelo corpuscular admitindo que a velocidade da luz no meio 1, $v_{1}$ , é diferente da velocidade da luz no meio 2, $v_{2}$ , e que na interface entre os dois meios atuam sobre as partículas de luz forças perpendiculares à superfície de separação. No caso do raio que passa do meio 1 para o meio 2, escolhendo o eixo $x$ paralelo à superfície de separação e o eixo $y$ perpendicular a ela, as componentes $v_{1x}$ e $v_{2x}$ das velocidade dos raios refletido e refratado são iguais entre si e iguais à componente $v_{1x}$ da velocidade do raio incidente, por não existirem forças na direção $x$ . A componente perpendicular da velocidade do raio refletido muda de sinal, mas a velocidade dos raios incidente e refletido é a mesma, $v_{1}$ . Os senos dos ângulo entre os raios incidente e refletido com a perpendicular são ambos iguais a,

\sin\theta_{1}=\dfrac{v_{1x}}{v_{1}}

(12.2)

e, por isso, os ângulos de incidência e de reflexão são iguais.

Já no caso do raio refratado, com velocidade $v_{2}$ diferente da velocidade $v_{1}$ do raio incidente, enquanto que as componentes segundo $x$ são iguais, $v_{1x}=v_{2x}$ , o seno do ângulo de refração é,

\sin\theta_{2}=\dfrac{v_{1x}}{v_{2}}

(12.3)

e substituindo (12.2) e (12.3) na equação (12.1) conclui-se que o índice de refração do meio 2 relativo ao meio 1 será,

n_{21}=\dfrac{v_{2}}{v_{1}}

(12.4)

Se o meio 1 for ar e o meio 2 água, observa-se que $n_{21}>1$ , o que implica que, segundo a teoria corpuscular da luz, a velocidade da luz é maior na água do que no ar. A equação (12.4) explica também corretamente a relação observada entre índices de refração para diferentes substâncias; por exemplo, o índice de refração do vidro relativo à água é igual ao índice do vidro relativo ao ar, dividido pelo índice da água relativo ao ar.

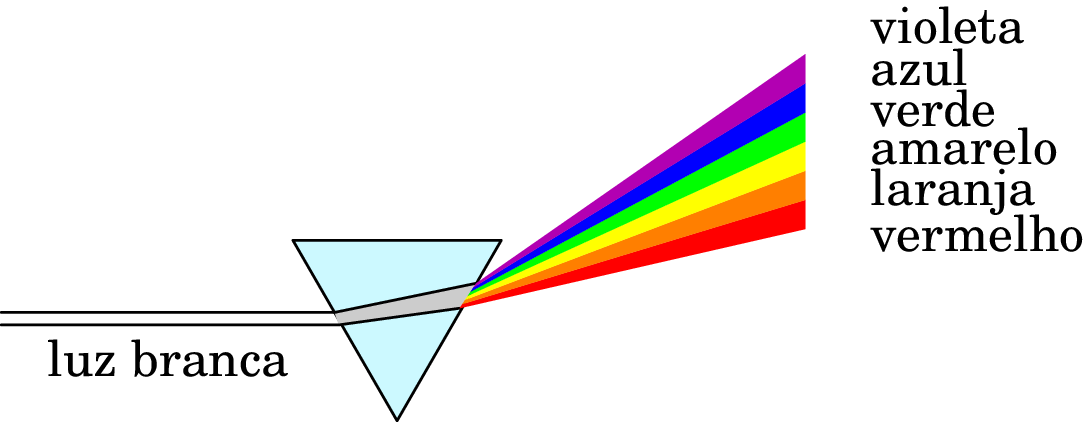
Newton explicou a separação da luz branca em diferentes cores, após a passagem por um prisma de vidro (figura 12.2), admitindo que a luz branca é composta por partículas de diferentes espécies (cores) que se deslocam com velocidades diferentes. As diferenças de velocidade faz com que partículas de diferentes cores sejam refratadas de forma diferente, na passagem do ar para o vidro do prisma e do vidro para o ar.

Figura 12.2: Dispersão da luz que atravessa um prisma.

12.1.2 Teoria ondulatória da luz

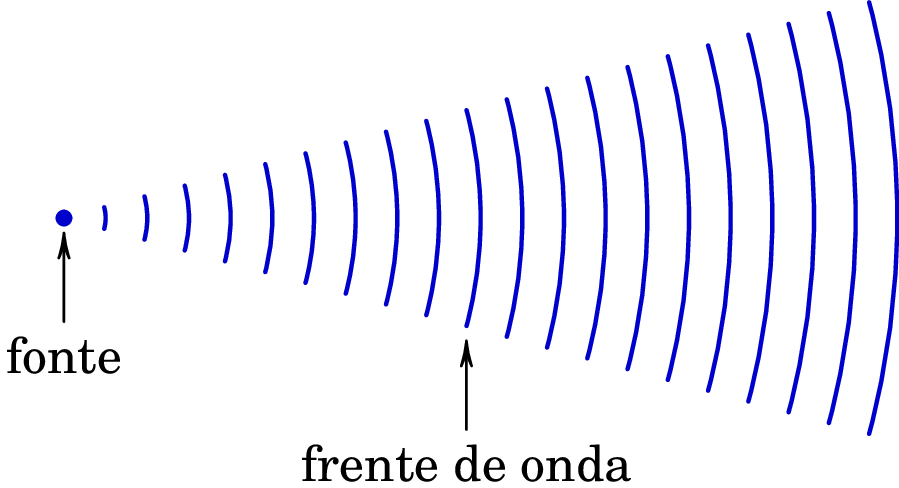
Na teoria ondulatória de Huygens um feixe de luz representa-se por uma parte de uma onda esférica, como na figura 12.3. Cada cor da luz corresponde a um comprimento de onda diferente e as frentes de onda (arcos paralelos na figura 12.3), que correspondem aos pontos onde a onda tem o seu valor máximo, deslocam-se com a velocidade da luz. A separação entre as frentes de onda é igual ao comprimento de onda.

Figura 12.3: Representação de um feixe de luz segundo a teoria ondulatória.

Usando lentes é possível focar a luz deformando as frentes de onda e um raio de luz é uma onda plana, em que as frentes de onda são planos paralelos entre si e perpendiculares à direção de propagação do raio. A figura 12.4 mostra a representação, segundo a teoria ondulatória, de um raio de luz que é refletido e refratado na interface entre dois meios diferentes. Os dois pontos A e B na figura fazem parte duma mesma frente de onda. O ponto B chega à superfície de interface no ponto C, um tempo $\Delta t$ após o ponto A ter chegado a ela, onde $\Delta t$ é o tempo que a luz demora a deslocar-se a distância $\overline{\mathrm{BC}}$ no meio 1:

\Delta t=\dfrac{\overline{\mathrm{BC}}}{v_{1}}

(12.5)

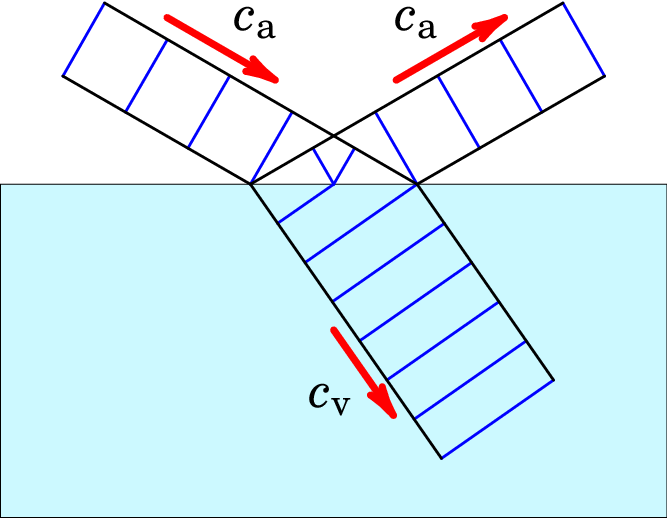
Reflexão e refração de uma onda de luz numa barra de vidro. — Figura 12.4: Reflexão e refração de uma onda de luz na passagem entre dois meios diferentes.

Quando o ponto C na onda é refletido no meio 1, o outro extremo dessa frente de onda já se deslocou a distância $\overline{\mathrm{AD}}$ , igual à velocidade da luz $v_{1}$ no meio 1 vezes $\Delta t$ , e a equação (12.5) mostra que $\overline{\mathrm{AD}}=\overline{\mathrm{BC}}$ . O ângulo de incidência na figura 12.4 é $\angle\mathrm{BAC}$ e o ângulo de reflexão é $\angle\mathrm{DCA}$ . A igualdade $\overline{\mathrm{AD}}=\overline{\mathrm{BC}}$ mostra que os ângulos de incidência e de reflexão são iguais.

O ângulo de refração é $\angle\mathrm{ECA}$ . Quando o ponto C entra no meio 2, o ponto A já se deslocou a distância $\overline{\mathrm{AE}}$ , igual ao tempo (12.5) vezes a velocidade $v_{2}$ da luz no meio 2:

\overline{\mathrm{AE}}=\dfrac{v_{2}}{v_{1}}\,\overline{\mathrm{BC}}

(12.6)

O índice de refração do meio 2 relativo ao meio 1 é,

n_{21}=\dfrac{\sin\angle\mathrm{BAC}}{\sin\angle\mathrm{ECA}}=\dfrac{\overline{\mathrm{BC}}}{\overline{\mathrm{AE}}}=\dfrac{v_{1}}{v_{2}}

(12.7)

que é a relação oposta da expressão (12.4) obtida no modelo corpuscular da luz. Alguma das duas equações (12.4) ou (12.7) deverá estar errada. Se a velocidade da luz for maior na água do que no ar, o modelo corpuscular estará correto e o modelo ondulatório errado; mas se a velocidade da luz for menor na água do que no ar, o modelo correto será o modelo ondulatório. Hoje em dia sabemos que a velocidade da luz é menor na água do que no ar, mas na época de Newton e Huygens não era possível medir essa diferença de velocidades e o prestígio de Newton fez com que fosse dada maior credibilidade à teoria corpuscular do que à teoria ondulatória.

Mais tarde foram descobertos novos fenómenos para os quais a teoria ondulatória tinha uma explicação mais simples do que a teoria corpuscular. Um desses fenómenos é a polarização quando a luz atravessa um certo tipo de cristal polarizador. Cada polarizador tem um eixo e se dois polarizadores forem colocados, um a seguir ao outro e com os seus eixos perpendiculares, não passará nenhuma luz através do sistema. Efeito esse que é aproveitado nos ecrãs de cristal líquido (LCD, siglas do termo inglês Liquid Crystal Display). Os pontos negros no ecrã correspondem a regiões onde o cristal está polarizado perpendicularmente a um filtro polarizador por cima do cristal.

No início do século XIX Thomas Young (1773–1829) deu o golpe de graça à teoria corpuscular da luz, com a sua experiência de interferência da luz que passa através de duas fendas muito próximas (figura 12.5).

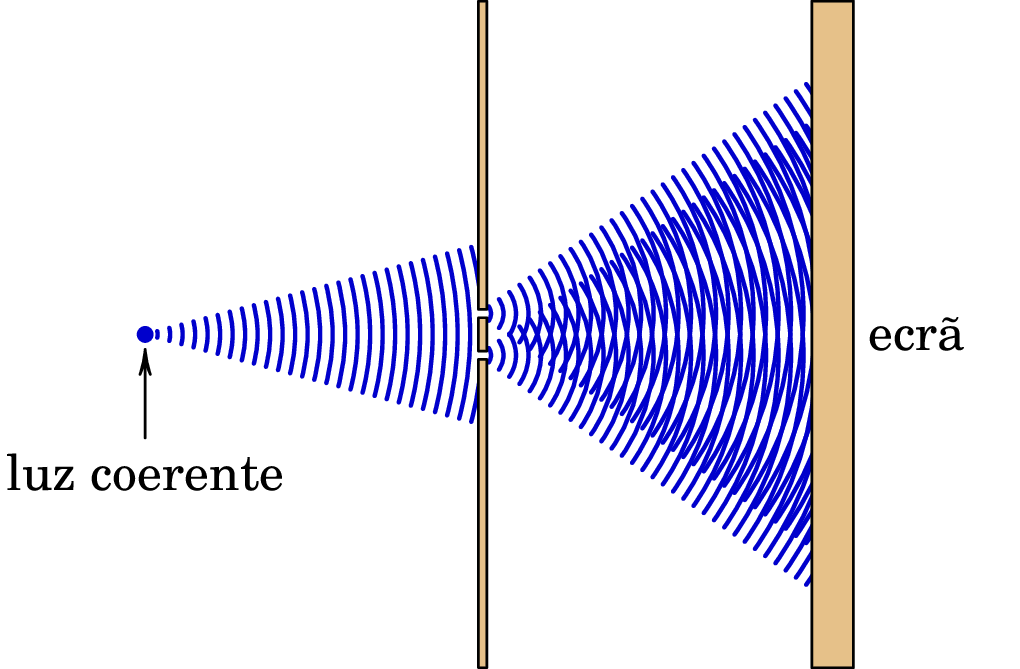
Figura 12.5: Interferência da luz após a passagem por duas fendas.

Se a luz fossem partículas, esperava-se que após a passagem pelas duas fendas, a maior parte delas chegassem ao ecrã próximas dos dois pontos exatamente em frente das duas fendas. No entanto, o que se observa são várias franjas claras e escuras no ecrã, que é um padrão de interferência caraterístico das ondas. Na figura 12.5 são visíveis essas zonas claras e escuras no ecrã. Nas zonas claras encontram-se as frentes de onda das duas ondas provenientes das duas fendas, produzindo interferência construtiva. Nas zonas escuras, uma frente de onda de uma das duas ondas (máximo) encontra-se com um ponto meio entre duas frentes de onda da segunda (mínimo), produzindo interferência destrutiva. O mesmo padrão de interferência é observado entre ondas de outros tipos, por exemplo, as ondas na superfície de um líquido, e a medição da distância entre as zonas claras e escuras permite determinar o comprimento de onda.

12.2 Espetro eletromagnético

As experiências de interferência da luz deixaram estabelecido que a luz é uma onda, mas o que é que está a oscilar nessas ondas? Como vimos no capítulo 11, Maxwell mostrou que o que oscila nessas ondas são campos elétrico e magnético, mas não conseguiu chegar a produzir ondas eletromagnéticas com dispositivos elétricos.

Hoje em dia grande parte das tecnologias que usamos dependem das ondas eletromagnéticas: ondas de rádio, micro-ondas, telemóveis, Bluetooth e GPS, entre muitas outras. A figura 12.6 mostra o princípio de produção e recepção de ondas eletromagnéticas; uma antena ligada a uma fonte de tensão alternada, com frequência $f$ da ordem de grandeza $c/\ell$ , onde $c$ é a velocidade da luz e $\ell$ o tamanho da antena, produz ondas eletromagnéticas de comprimento de onda $\lambda$ com a ordem de grandeza de $\ell$ . Ondas essas que podem ser detetadas por outra antena remota, com tamanho da ordem de grandeza do comprimento de onda $\lambda$ .

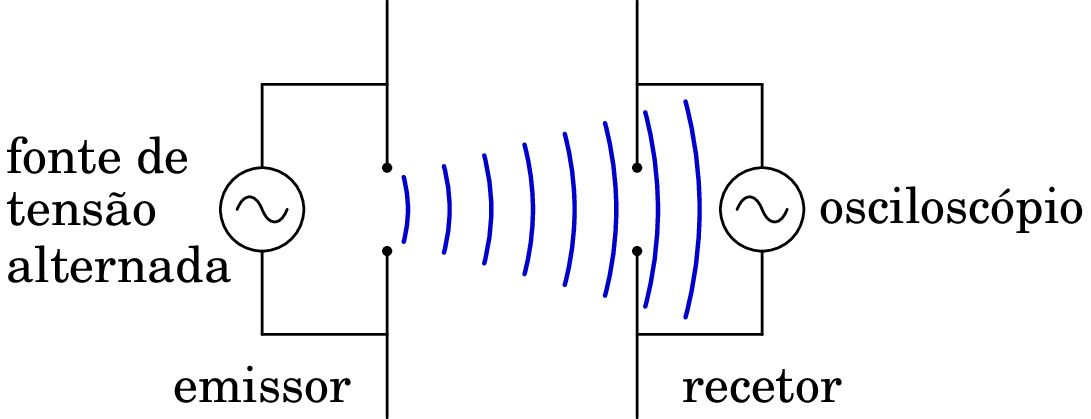
Figura 12.6: Produção e detecção de uma onda eletromagnética.

O comprimento de onda, $\lambda$ , e a frequência, $f$ , de uma onda eletromagnética harmónica não podem variar independentemente, pois estão relacionados por $\lambda f=c$ . Dada a frequência, ou o comprimento de onda, é possível classificar a onda dentro do espetro eletromagnético e determinar as suas propriedades. O valor máximo dos campos determina a intensidade da onda, mas não as suas propriedades.

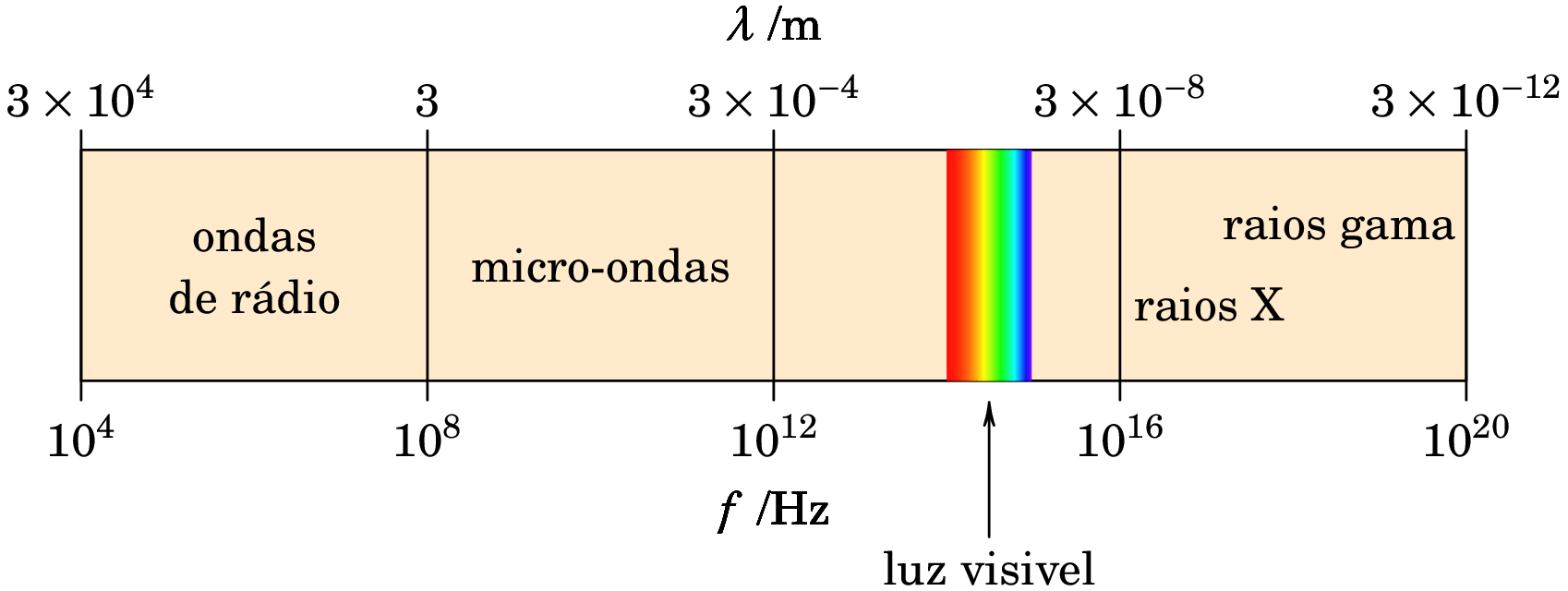
Em princípio, podem existir ondas eletromagnéticas com qualquer valor de $\lambda$ entre 0 e $\infty$ . Alguns exemplos de ondas eletromagnéticas são as ondas de rádio e de comunicações móveis, as ondas usadas num forno de micro-ondas para aquecer os alimentos e a luz visível. O que distingue essas ondas é a sua frequência, ou, de forma equivalente, o seu comprimento de onda. A figura 12.7 mostra o espetro eletromagnético conhecido e a posição de algumas ondas comuns nesse espetro.

Usualmente, a radiação eletromagnética produzida por um sistema não tem uma frequência única $f$ , como no caso das ondas harmónicas, mas é uma sobreposição de ondas harmónicas com uma distribuição de frequências. Por exemplo, a luz solar tem um espetro contínuo de frequências na banda visível, que pode ser observado usando um prisma, tal como na figura 12.2.

Vimos que a velocidade das ondas eletromagnéticas no vácuo é a velocidade $c$ da luz no vácuo, igual a:

c=\sqrt{\dfrac{k}{k_{\mathrm{m}}}}

(12.8)

onde $k$ é a constante de Coulomb e $k_{\mathrm{m}}$ a constante magnetostática. Os meios em que a luz pode propagar-se são não-condutores e não-magnéticos, onde a constante de Coulomb deverá ser dividida pela constante dielétrica $K$ e a constante magnetostática é praticamente igual à do vácuo. A velocidade da luz num meio é então,

v=\dfrac{c}{\sqrt{K}}

(12.9)

O índice de refração $n$ de um meio, definido em relação ao vácuo, é assim igual à raiz quadrada da sua constante dielétrica (equação (12.7)):

n=\dfrac{c}{v}=\sqrt{K}

(12.10)

relação essa que é corroborada experimentalmente.

A constante dielétrica que temos usado em capítulos anteriores é para campos eletrostáticos. No caso do campo elétrico variável das ondas eletromagnéticas, a constante dielétrica depende da frequência. Isso explica porque as diferentes cores num feixe de luz são desviadas de forma diferente na passagem através dum prisma de vidro. A figura 12.2 mostra que o índice de refração do vidro é maior para a luz violeta do que para a luz vermelha; como tal, no intervalo de frequências da luz visível, a constante dielétrica do vidro aumenta com a frequência da onda.

O arco-íris é outra manifestação desse mesmo fenômeno (dispersão da luz). A luz do Sol atravessa gotas de água nas nuvens e parte dessa luz é refletida de volta; se não houvesse dispersão, olhando para uma nuvem formada por pequenas gotas de água, veríamos um ponto de luz intensa, refletida, na direção oposta à nossa posição em relação ao Sol. A dispersão da luz dentro das gotas de água faz com que esse ponto de luz refletida se torne num anel, com um ângulo de aproximadamente 42 ${}^{\circ}$ , à volta desse ponto. Como a dispersão das diferentes cores é diferente, em vez de um único anel formam-se vários anéis das diferentes cores. A cor que sofre maior refração (violeta) acaba por ficar no anel mais próximo do centro, porque a reflexão na superfície interna da gota inverte a ordem das cores. Por vezes é possível observar o segundo arco íris, com raio maior do que o primeiro, que corresponde à reflexão da luz duas vezes dentro das gotas de água antes de sair refratada; as cores nesse segundo arco íris aparecem na ordem inversa do primeiro: o arco vermelho mais próximo do centro do que o arco violeta.

12.3 Efeito fotoelétrico

Na mesma experiência em que Hertz produziu no laboratório ondas eletromagnéticas pela primeira vez, descobriu também o efeito fotoelétrico. Quando a luz incide num condutor ou semicondutor alguns eletrões são extraídos do material. Esse é o princípio usado para produzir corrente elétrica a partir da luz nas células fotovoltaicas como a da figura 12.8. A luz que incide num semicondutor de tipo p faz com que alguns eletrões passem para o condutor de tipo n, podendo produzir corrente elétrica num dispositivo.

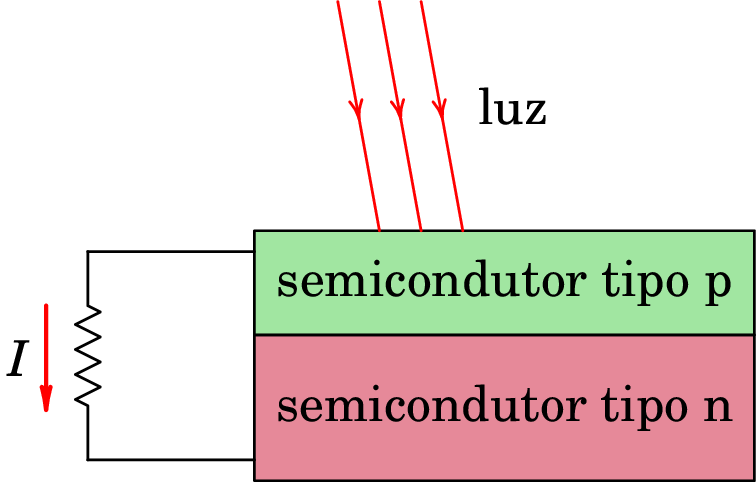
A célula fotovoltaica atua como uma fonte de f.e.m., com cátodo no semicondutor de tipo p e ânodo no semicondutor de tipo n. A intensidade da corrente aumenta com a intensidade da luz incidente, como era de esperar. No entanto o que é inesperado é que o valor da f.e.m. depende da frequência da luz e não da sua intensidade. Diferentes materiais possuem uma frequência limiar por baixo da qual não é produzido efeito fotoelétrico, qualquer que seja a intensidade da luz. E quanto maior for a frequência em relação à frequência limiar, maior será o valor da f.e.m.

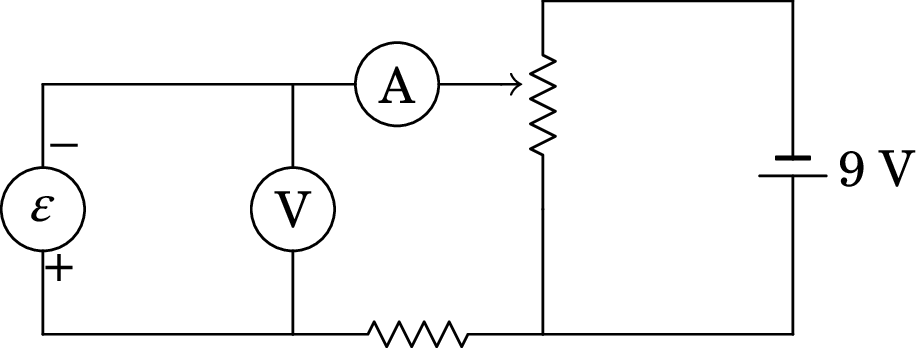
O valor da f.e.m. de uma célula fotovoltaica pode ser determinado com o circuito representado na figura 12.9. O círculo à esquerda representa a célula fotoelétrica, com f.e.m. $\varepsilon$ , que está a fornecer corrente a uma resistência $R$ . Um voltímetro, indicado com a letra V, está ligado em paralelo com a célula e um amperímetro, indicado pela letra A, está ligado em série com a resistência $R$ . A f.e.m. de 9 V junto com o potenciómetro de resistência $r$ constituem uma fonte variável, oposta à célula, com voltagem que pode ser ajustada mudando a posição do potenciómetro. Aumentando gradualmente a voltagem da fonte variável a partir de 0, a intensidade da corrente indicada no amperímetro diminui até que, quando ficar igual a zero, a diferença de potencial $\Delta V$ registada no voltímetro, será igual ao valor $\varepsilon$ da f.e.m. da célula.

Figura 12.9: Circuito usado para determinar a f.e.m. de uma célula fotovoltaica.

A figura 12.10 mostra o resultado obtido com um circuito como o da figura 12.9, variando a frequência $f$ da luz incidente e para dois materiais fotoelétricos diferentes. O primeiro material tem frequência mínima $f_{1}$ e o segundo tem frequência mínima $f_{2}$ . No eixo das ordenadas, a f.e.m. $\varepsilon$ foi multiplicada pela carga elementar $e$ para facilitar a interpretação que será feita a seguir. O produto $e\,\varepsilon$ é a energia que a célula fotoelétrica fornece a cada eletrão de condução. Não é óbvio porque existe uma frequência mínima para cada material nem porque os gráficos são retas e com o mesmo declive no caso de diferentes materiais. Deverá existir alguma grandeza fundamental que determina o valor do declive.

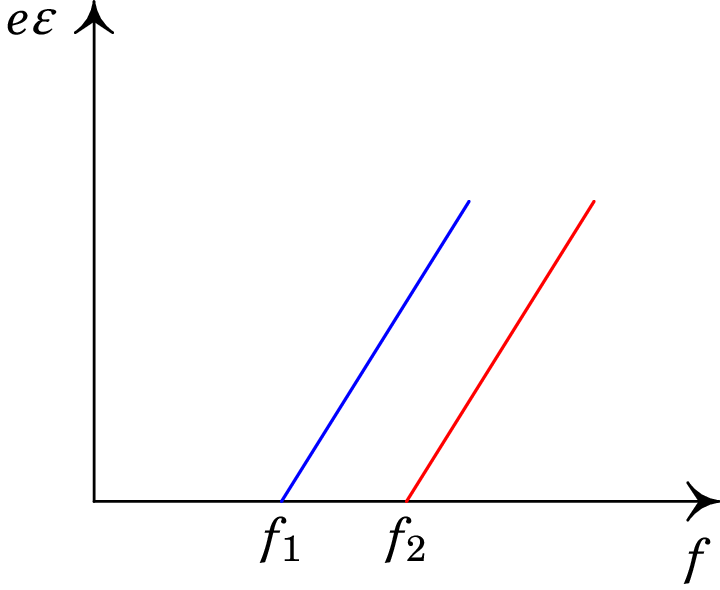
Energia dos eletrões emitidos por efeito fotoelétrico em
dois materiais diferentes, em função da frequência da luz. — Figura 12.10: Energia dos eletrões emitidos por efeito fotoelétrico em dois materiais diferentes, em função da frequência da luz.

O efeito fotoelétrico foi finalmente explicado por Albert Einstein (1879–1955), num artigo de 1905 que lhe valeu a atribuição do premio Nobel da Física. A explicação de Einstein é bastante simples, mas revolucionária. Começa pela constatação de que o declive no gráfico 12.10 é exatamente igual à constante de Planck:

h=6.626\times 10^{-34}\;\mathrm{J}\cdot\mathrm{s}

(12.11)

que alguns anos antes tinha sido postulada por Max Planck (1858–1947) para explicar o espetro de radiação do corpo negro, admitindo que as oscilações do objeto que produz radiação ocorrem com energias que são múltiplos inteiros dessa constante $h$ . Einstein defende que a luz está formada por partículas, chamadas fotões, cada uma com energia $h\,f$ , que depende apenas da sua frequência $f$ . A equação das retas na figura 12.10 é:

e\varepsilon=hf-\phi\qquad(\mbox{se:}\quad hf>\phi)

(12.12)

Em que $-\phi$ é a ordenada na origem (se as retas se estendessem até o lado negativo da energia $e\varepsilon$ ). Quando um fotão colide com um eletrão no material, a sua energia é absorvida pelo eletrão e se essa energia for maior que $\phi$ , o eletrão é libertado do material ficando com energia igual à energia do fotão absorbido menos a energia $\phi$ necessária para libertar o eletrão. A constante $\phi$ , caraterística de cada material , designa-se por função de trabalho.

12.4 Díodos emissores de luz (LED)

Os díodos emissores de luz (LED) são dispositivos com um cátodo e um ânodo, identificados como mostra a figura 12.11. Ligando uma diferença de potencial superior a um valor mínimo, com o ânodo a maior potencial que o cátodo, o LED produz luz monocromática. Quando o potencial do ânodo for menor que o potencial do cátodo, o LED não deixa passar corrente e não produz luz.

LED e diagrama de circuito correspondente. O cátodo costuma ser
um fio mais curto e estar perto de uma zona onde a cobertura plástica é
plana. — Figura 12.11: LED e diagrama de circuito correspondente. O cátodo costuma ser um fio mais curto e estar perto de uma zona onde a cobertura plástica é plana.

A energia elétrica que os portadores de carga perdem na passagem da interface entre os dois semicondutores é transformada em luz. Essa energia corresponde à diferença entre os níveis de energia dos semicondutores no LED e tem um valor específico próprio desses semicondutores. O efeito de produção de um fotão pela perda de energia de um eletrão de condução é o simétrico do efeito fotoelétrico em que um fotão é absorvido passando a sua energia para um eletrão de condução.

Como vimos, a energia que transporta cada fotão é igual a $h f$ . Como tal, os fotões emitidos no LED têm todos aproximadamente a mesma frequência, igual à diferença entre os níveis de energia dos eletrões nos dois elétrodos do LED, dividida pela constante de Planck; isso implica que a luz do LED é monocromática. Assim, a cor da luz emitida pelo LED depende do semicondutor usado. A tabela 12.1 mostra as cores próprias de alguns semicondutores.

Tabela 12.1: Cores de alguns LED.

Semicondutores	Cor da luz	$\lambda$ (nm)
GaAlAs/GaAs	Infravermelha	880
GaAlAs/GaAs	Vermelha	660
GaAsP/GaP	Amarela	585
GaP/GaP	Verde	555
GaN/SiC	Azul	470

(Fonte: https://zeiss-campus.magnet.fsu.edu/print/lightsources/leds-print.html.)

Quando circula corrente elétrica pelo LED, cada carga de condução que atravessa a interface no LED perde a energia correspondente à energia $h f$ de um fotão. Como tal, a curva caraterística tensão-corrente do LED é semelhante à caraterística de um recetor, com ordenada na origem positiva, e declive constante positivo (figura 12.12).

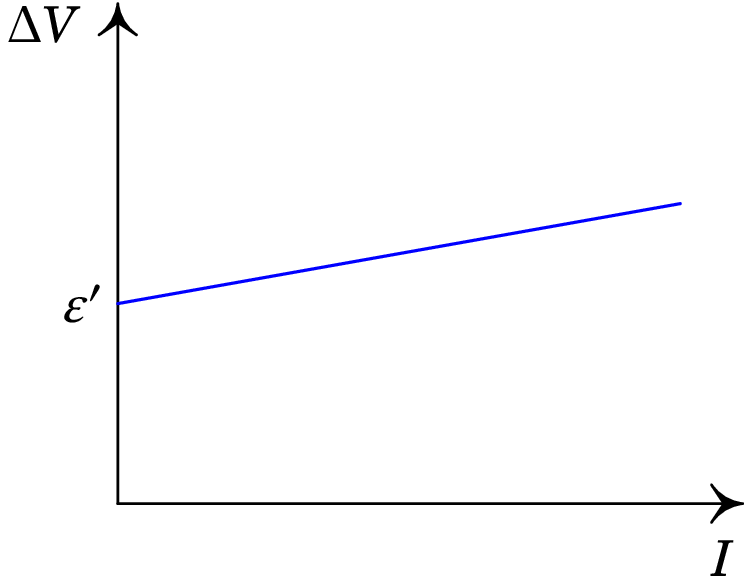
Figura 12.12: Caraterística tensão-corrente de um LED.

A força contra-eletromotriz do LED, $\varepsilon^{\prime}$ (ordenada na origem da curva caraterística tensão-corrente), é a energia por unidade de carga que as cargas de condução perdem na passagem pelo LED, sendo convertida em luz.

Assim, a energia que cada eletrão perde quando atravessa a interface entre os dois semicondutores é igual a: $e\,\varepsilon^{\prime}$ . Energia essa que é igual à energia do fotão emitido:

e\,\varepsilon^{\prime}=h\,f=\dfrac{h\,c}{\lambda}

(12.13)

onde $c$ é a velocidade da luz e $\lambda$ é o comprimento de onda da luz emitida.

Resolvendo a equação 12.13 em ordem a $h$ obtém-se:

h=\dfrac{e\varepsilon^{\prime}\lambda}{c}

(12.14)

Esta equação pode ser usada para medir experimentalmente o valor da constante de Planck, a partir da caraterística tensão-corrente de um LED usando um circuito como o da figura 12.13 (observe-se a semelhança com o circuito 12.9).

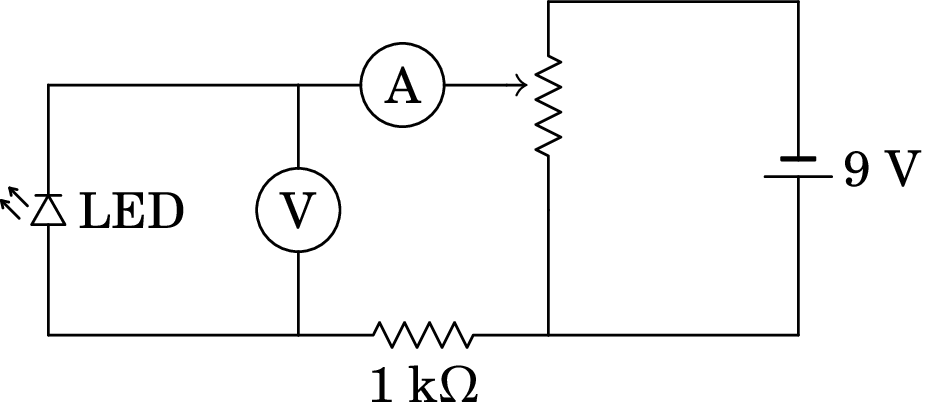
Circuito usado para determinar a caraterística de um
LED. — Figura 12.13: Circuito usado para determinar a caraterística de um LED.

A resistência de 1 k $\Omega$ é usada para evitar que a corrente no LED ultrapasse alguns miliampere, queimando o LED; se o LED estiver ligado no sentido correto, deverá produzir luz. Com os valores medidos da diferença de potencial em função da corrente traça-se a curva caraterística do LED, que pode ser ajustada por uma reta. A ordenada na origem dessa reta, $\varepsilon^{\prime}$ , e o valor do comprimento de onda próprio do LED (tabela 12.1) permitem obter o valor da constante de Planck a partir da equação 12.14.

Os LED são muito usados atualmente porque uma lâmpada de LED é muito mais eficiente que outros tipos de lâmpadas. A maior parte da energia elétrica fornecida a uma lâmpada de LED é transformada em energia dos fotões.

12.5 Dualidade onda-partícula

Não só a luz, que é claramente uma onda eletromagnética, comporta-se também como partículas (fotões), mas têm sido feitas experiências em que neutrões, que são claramente partículas, interferem entre si produzindo padrões de interferência de ondas.

Na física atual os fotões ou qualquer outra partícula têm também uma natureza ondulatória. A energia de um fotão e das outras partículas é produzida ou absorvida em quantidades discretas, mas é transportada de um ponto para outro na forma de uma onda. Todas as formas de matéria e energia apresentam propriedades de onda e de partícula. Essa dualidade onda-partícula é a base da física quântica.

Numa onda clássica, a energia pode ser absorvida de forma contínua; i.e., a onda pode transferir qualquer parte da sua energia a um sistema. No caso de uma onda quântica, como as ondas eletromagnéticas, a transferência de energia a um sistema só pode ser feita por absorção de alguns fotões; a energia transferida é a soma das energias desses fotões e, portanto, deve ser um múltiplo inteiro do quantum de energia $h f$ .