11. Ondas eletromagnéticas

James Clerk Maxwell (1831–1879)

Maxwell chegou à conclusão que a lei de Ampère só poderia ser válida em casos particulares, quando o campo elétrico fosse estático, e mostrou que acrescentando outro termo, a corrente de deslocamento, proporcional à variação temporal do fluxo elétrico, obtinha-se uma equação válida também no caso em que existe campo elétrico não-estático. Maxwell sintetizou toda a teoria eletromagnética em 4 equações, conhecidas como equações de Maxwell, e mostrou que é possível existirem campos elétrico e magnético, variáveis, inclusivamente quando não existem nem cargas nem correntes. Campos esses que são induzidos mutuamente pelas suas variações e que dão origem a uma onda eletromagnética que se desloca com velocidade constante que depende apenas das constantes $k$ e $k_{\mathrm{m}}$. Sendo o valor previsto dessa velocidade igual à velocidade da luz, Maxwell postulou que a própria luz deveria ser uma dessas ondas eletromagnéticas; mas teriam de passar oito anos após a morte de Maxwell antes que a existência das ondas eletromagnéticas fosse corroborada numa experiência no laboratório.

11.1 Corrente de deslocamento

Maxwell percebeu que a lei de Ampère (8.8) só podia ser válida no caso em que o campo elétrico é estático. Se assim não for, deve-se acrescentar à corrente $I_{\mathrm{C}}$ através da curva C outra corrente $I_{\mathrm{d}}$, denominada por corrente de deslocamento. A equação obtida é desginada de lei de Ampère-Maxwell:

$${\oint }_{\mathrm{C}}\overrightarrow{B}\cdot d\overrightarrow{r}=4\pi k_{\mathrm{m}}\left(I_{\mathrm{C}}+I_{\mathrm{d}}\right)$$ (11.1)

A lei de Ampère é válida unicamente nos casos em que o campo elétrico é estático ou nulo, fazendo com que a corrente de deslocamento seja nula. O integral de linha do campo $\overrightarrow{B}$, numa curva fechada C, pode ser diferente de zero inclusivamente quando não passa corrente $I_C$ através da curva, devido à corrente de deslocamento. Corrente essa que deverá depender da derivada temporal do fluxo elétrico através do interior da curva C, tal como na lei de Faraday (9.28) a derivada temporal do fluxo magnético produz integral de linha do campo $\overrightarrow{E}$ ao longo de uma curva fechada C.

Para mostra como é expressão da corrente de deslocamento em função do fluxo elétrico, consideremos o exemplo de um fio retilíneo sobre o semieixo negativo $z$, que se estende desde $-\mathrm{\infty }$ até a origem (figura 11.1).

Figura 11.1: Fio retilíneo no semieixo negativo $z$, com corrente $I$.

Se durante alguns instantes há corrente $I$ no fio, no sentido positivo do eixo $z$, haverá acumulação de cargas positivas na origem. A carga acumulada na origem, $q(t)$, é uma função do tempo e a intensidade da corrente no fio é igual à derivada dessa função em ordem ao tempo:

$$I=\frac{\mathrm{d}q}{\mathrm{d}t}$$ (11.2)

Como existe simetria cilíndrica, as linhas do campo magnético produzido pela corrente no fio são circunferências perpendiculares ao eixo $z$, com centro nele, orientadas no sentido da regra da mão direita segundo a direção positiva do eixo $z$. Seja C uma circunferência perpendicular ao eixo $z$, de raio $\varrho$ e com centro no ponto de coordenada $z$ no eixo $z$ (ver figura 11.1). A curva C coincide com uma curva de campo $\overrightarrow{B}$ e escolhendo o sentido de C no sentido do campo, o integral de linha de $\overrightarrow{B}$ ao longo de C é igual a $2\pi \varrho B$; usando a lei de Ampère-Maxwell (11.1), obtém-se o módulo do campo nos pontos com coordenada $z$ e a uma distância $\varrho$ do eixo do fio:

$$B=\frac{2k_{\mathrm{m}}\left(I_{\mathrm{C}}+I_{\mathrm{d}}\right)}{\varrho }$$ (11.3)

O gráfico 11.2 mostra o módulo do campo magnético esperado, a uma distância fixa $\varrho$ do eixo $z$ e variando a coordenada $z$ (centro das circunferências C). Longe da origem, com $|z|\to \mathrm{\infty }$, a corrente de deslocamento é nula (a acumulação de cargas na origem não interessa). No limite $z\to -\mathrm{\infty }$ a corrente através da curva é $I_{\mathrm{C}}=I$ e a equação (11.3) conduz a $B=2k_{\mathrm{m}}I/\varrho$. No limite $z\to \mathrm{\infty }$ a corrente através da curva é nula e o campo também é nulo.

Figura 11.2: Campo $B$ do fio retilíneo no semieixo negativo $z$, com corrente $I$, nos pontos a uma distância $\varrho$ do eixo $z$.

Em $z=0$ espera-se que $B$ tenha o valor intermédio $k_{\mathrm{m}}I/\varrho$ e próximo da origem a corrente de deslocamento será importante para produzir o resultado da figura 11.2. O gráfico da figura 11.3 mostra a corrente $I_{\mathrm{C}}$ através da circunferência C, em função da posição $z$ do seu centro (linha contínua a vermelho) e a corrente de deslocamento (linha azul a tracejado) necessária para produzir o resultado da figura 11.2.

Figura 11.3: Correntes $I_{\mathrm{C}}$ e $I_{\mathrm{d}}$ através da circunferência C no exemplo da figura 11.1.

A carga $q$ produz campo elétrico $\overrightarrow{E}$ e, portanto, fluxo elétrico ${\mathrm{\Psi }}_{\mathrm{S}}$ através da superfície S delimitada pela circunferência C. O fluxo é negativo se o centro da circunferência estiver em , positivo se o centro estiver em $z>0$ ou nulo se o centro estiver em $z=0$. Quando $z$ aproxima-se de zero, o fluxo através da circunferência aproxima-se de metade do fluxo total $4\pi kq$. Em o fluxo aproxima-se de $-2\pi kq$ na origem e em $z>0$ aproxima-se $2\pi kq$ na origem. Tendo em conta a relação (11.2) entre a carga $q$ e a corrente no fio, o gráfico da derivada do fluxo elétrico ${\mathrm{\Psi }}_{\mathrm{S}}$ é como mostra a figura 11.4, passando de $-2\pi kI$ para $2\pi kI$ na origem.

Figura 11.4: Derivada temporal do fluxo elétrico através das circunferências com centro em $z$.

Comparando o gráfico da figura 11.4 com a curva a tracejado na figura 11.3, conclui-se que a corrente de deslocamento deverá ser dada pela seguinte expressão:

$$I_{\mathrm{d}}=\frac{1}{4\pi k}\frac{\mathrm{d}{\mathrm{\Psi }}_{\mathrm{S}}}{\mathrm{d}t}=\frac{1}{4\pi k}{\iint }_{\mathrm{S}}\frac{\partial \overrightarrow{E}}{\partial t}\cdot d\overrightarrow{A}$$ (11.4)

Exemplo 11.1

Um fio retilíneo de comprimento $\mathrm{\ell }$ é percorrido por corrente de intensidade $I$. Usando a lei de Ampère-Maxwell, determine o módulo do campo magnético produzido a uma distância $\varrho$ do fio e mostre que o resultado é o mesmo que foi obtido no exemplo 8.1, usando a lei de Biot-Savart.

Resolução. Os pontos à mesma distância $\varrho$ do fio e equidistantes de um dos extremos são equivalentes e, portanto, as linhas de campo são circunferências C perpendiculares ao fio, com centro nele, e no sentido da regra da mão direita segundo a direção da corrente, tal como mostra a figura seguinte.

Aplicando a lei de Ampère-Maxwell, obtém-se mesma expressão (11.3) para o módulo do campo. A corrente no fio finito implica acumulação de cargas, $q_1$ e $q_2$, nos dois extremos, com derivadas:

$$\frac{\mathrm{d}{q}_1}{\mathrm{d}t}=-I\mathit{\hspace{1em}\hspace{1em}}\frac{\mathrm{d}{q}_2}{\mathrm{d}t}=I$$

Cargas essas que produzem fluxo elétrico variável e corrente de deslocamento $I_{\mathrm{d}}$ através do interior da circunferência C:

$$I_{\mathrm{d}}=\frac{1}{4\pi k}\left(\frac{\mathrm{d}{\mathrm{\Psi }}_1}{\mathrm{d}t}+\frac{\mathrm{d}{\mathrm{\Psi }}_2}{\mathrm{d}t}\right)$$

onde ${\mathrm{\Psi }}_1$ e ${\mathrm{\Psi }}_2$ são os fluxos elétricos produzidos por $q_1$ e $q_2$. Cada um desses fluxos é igual ao fluxo através da calota esférica que C delimita na esfera com centro em $q_i$ ($i$ igual a 1 ou 2), e raio $r_i$. Nessas esferas o campo elétrico é perpendicular e com valor $k{q}_i/r_i^2$; o fluxo ${\mathrm{\Psi }}_i$ é igual a esse valor do campo vezes área da calota, que pode ser calculada integrando o elemento diferencial de área da esfera,em coordenadas esféricas (equação (A.57)), com ângulo zenital entre 0 e ${\theta }_i$ (ver figura acima):

$$A_i=r_i^2{\int }_0^{2\pi }{\int }_0^{{\theta }_i}\sin \theta \mathrm{d}\theta \mathrm{d}\varphi =2\pi r_i^2(1-\cos {\theta }_i)$$

e multiplicando pelos valores dos campos elétricos, os fluxos elétricos são:

$${\mathrm{\Psi }}_i=2\pi kq(1-\cos {\theta }_i)$$

A derivada temporal de ${\mathrm{\Psi }}_i$ é a mesma expressão de ${\mathrm{\Psi }}_i$, substituindo $q$ por $\pm I$. Na figura acima observa-se que a variação de ambos fluxos é no sentido negativo da curva C e, como tal, a corrente de deslocamento é igual a:

$$I_{\mathrm{d}}=\frac{I}{2}(\cos {\theta }_1+\cos {\theta }_2-2)$$

A corrente $I_{\mathrm{C}}$ através de C é igual a $I$ (se o centro de C estiver sobre o fio, como na figura acima). A corrente total é,

$$I_{\mathrm{C}}+I_{\mathrm{d}}=\frac{I}{2}(\cos {\theta }_1+\cos {\theta }_2)$$

e substituindo na equação (11.3) obtém-se o mesmo resultado do exemplo 8.1:

$$B=\frac{k_{\mathrm{m}}I}{\varrho }(\cos {\theta }_1+\cos {\theta }_2)$$

No caso em que o centro da circunferência C estiver fora do fio, $I_C$ será nula, o fluxo produzido pela carga mais próxima de C, por exemplo $q_2$, mudará de sinal e a calota esférica com centro em $q_2$ terá ângulo $\pi -{\theta }_2$. Assim, a corrente total nesse caso será,

$I_{\mathrm{C}}+I_{\mathrm{d}}$ $=I_{\mathrm{d}}={\displaystyle \frac{I}{2}}\left(\cos {\theta }_1-1-\cos (\pi -{\theta }_2)+1\right)$

$={\displaystyle \frac{I}{2}}(\cos {\theta }_1+\cos {\theta }_2)$

e a expressão para $B$ é a mesma obtida quando o centro de C está sobre o fio.

Observe-se que a corrente de deslocamento garante a continuidade da corrente total através da circunferência C, quando o seu centro passa de do fio para fora dele.

11.2 Equações de Maxwell

As quatro equações de básicas do eletromagnetismo, conhecidas como equações de Maxwell, são as equações que permitem calcular os campos elétrico e magnético, em qualquer ponto de uma região onde as cargas e as correntes são conhecidas. A primeira equação de Maxwell é a lei de Gauss (2.20) que, como vimos é:

$${∯}_{\mathrm{S}}\overrightarrow{E}\cdot d\overrightarrow{A}=4\pi k{q}_{\text{int}}$$ (11.5)

A segunda equação de Maxwell é a lei de Faraday, que na forma (9.28), é:

$${\oint }_{\mathrm{C}}\overrightarrow{E}\cdot d\overrightarrow{r}=-{\iint }_{\mathrm{R}}\frac{\partial \overrightarrow{B}}{\partial t}\cdot d\overrightarrow{A}$$ (11.6)

A terceira equação é a equação (8.21), que expressa a impossibilidade da existência de monopolos magnéticos:

$${∯}_{\mathrm{S}}\overrightarrow{B}\cdot d\overrightarrow{A}=0$$ (11.7)

A quarta equação de Maxwell é a lei de Ampère-Maxwell (11.1), substituindo a expressão (11.4) da corrente de deslocamento em função do campo elétrico:

$${\oint }_{\mathrm{C}}\overrightarrow{B}\cdot d\overrightarrow{r}=4\pi k_{\mathrm{m}}{I}_{\mathrm{C}}+\frac{k_{\mathrm{m}}}{k}{\iint }_{\mathrm{R}}\frac{\partial \overrightarrow{E}}{\partial t}\cdot d\overrightarrow{A}$$ (11.8)

As quatro equações de Maxwell são válidas em qualquer curva fechada e orientada C, que delimita uma região R, e qualquer superfície fechada S (ver figura 11.5).

Figura 11.5: Curva e superfícies usadas nas equações de Maxwell.

As quatro equações de Maxwell podem ser escritas de forma diferencial. Na primeira e terceira equações, (11.5) e (11.7), o limite quando o volume dentro da superfície S aproxima-se de zero, dividido por esse volume, conduz à divergência do campo. Como tal, a forma diferencial da primeira e terceira equações é a seguinte:

$\overrightarrow{\nabla }\cdot \overrightarrow{E}=4\pi k\rho$ (11.9)

$\overrightarrow{\nabla }\cdot \overrightarrow{B}=0$ (11.10)

Onde $\rho$ é a densidade volúmica de carga, no ponto onde se calcula a divergência de $\overrightarrow{E}$. Na segunda e quarta equações, (11.6) e (11.8), o teorema de Stokes permite escrever os integrais de linha no lado esquerdo como integral de superfície, na região R, do rotacional do respetivo campo. E a corrente $I_{\mathrm{C}}$ através da curva C é igual ao integral de superfície da densidade de corrente, $\overrightarrow{J}$, na região R. Comparando os dois lados da equação, que deverão ser válidos para qualquer região R, obtém-se a forma diferencial da segunda e a quarta equações de Maxwell.

$\overrightarrow{\nabla }\times \overrightarrow{E}=-{\displaystyle \frac{\partial \overrightarrow{B}}{\partial t}}$ (11.11)

$\overrightarrow{\nabla }\times \overrightarrow{B}=4\pi k_{\mathrm{m}}\overrightarrow{J}+{\displaystyle \frac{k_{\mathrm{m}}}{k}}{\displaystyle \frac{\partial \overrightarrow{E}}{\partial t}}$ (11.12)

11.3 Ondas eletromagnéticas

No vácuo, onde não existem cargas nem correntes, as 4 equações de Maxwell (11.9), (11.11), (11.10), (11.12) ficam da forma seguinte:

$\overrightarrow{\nabla }\cdot \overrightarrow{E}$ $=0$ (11.13)

$\overrightarrow{\nabla }\times \overrightarrow{E}$ $=-{\displaystyle \frac{\partial \overrightarrow{B}}{\partial t}}$ (11.14)

$\overrightarrow{\nabla }\cdot \overrightarrow{B}$ $=0$ (11.15)

$\overrightarrow{\nabla }\times \overrightarrow{B}$ $={\displaystyle \frac{k_{\mathrm{m}}}{k}}{\displaystyle \frac{\partial \overrightarrow{E}}{\partial t}}$ (11.16)

Essas equações admitem muitas possíveis soluções. Antes de mostrarmos como resolver essas equações, observe-se que elas dependem de apenas um parámetro, a constante $k_{\mathrm{m}}/k$, que no sistema internacional de unidades tem o valor,

$$\frac{k_{\mathrm{m}}}{k}=\frac{{10}^{-7}\mathrm{T}\cdot \mathrm{m}\cdot {\mathrm{A}}^{-1}}{8.988\times {10}^9\mathrm{N}\cdot {\mathrm{m}}^2\cdot {\mathrm{C}}^{-2}}=\frac{1}{8.988\times {10}^{16}}\frac{{\mathrm{s}}^2}{{\mathrm{m}}^2}$$ (11.17)

que é exatamente igual ao inverso do quadrado da velocidade da luz no vácuo, $c=2.998\times {10}^8$ m/s

$$\frac{k_{\mathrm{m}}}{k}=\frac{1}{c^2}$$ (11.18)

Esta relação entre as constantes elétrica e magnética e a velocidade da luz, sugere que a luz deverá ser um fenómeno eletromagnético.

Admitindo que existam soluções em que o campo elétrico $\overrightarrow{E}$ aponta sempre na mesma direção, podemos definir o eixo $z$ nessa direção ficando assim $\overrightarrow{E}=E(x,y,z,t)\hat{k}$. Substituindo na primeira equação de Maxwell, (11.13), o resultado é,

$$\frac{\mathrm{d}E}{\mathrm{d}z}=0$$ (11.19)

i.e., $E$ não pode depender de $z$. A segunda equação de Maxwell, (11.14), conduz a,

$$\frac{\mathrm{d}E}{\mathrm{d}y}\hat{ı}-\frac{\mathrm{d}E}{\mathrm{d}x}\hat{ȷ}=-\frac{\mathrm{d}\overrightarrow{B}}{\mathrm{d}t}$$ (11.20)

A derivada de $\overrightarrow{B}$ deverá estar no plano $xy$, ou seja, o campo magnético deverá ser perpendicular ao campo elétrico. Se escolhermos o eixo $x$ na direção do campo magnético, teremos $\overrightarrow{B}=B(x,y,z,t)\hat{ı}$ e a equação (11.20) implica:

$$\frac{\mathrm{d}E}{\mathrm{d}y}=-\frac{\mathrm{d}B}{\mathrm{d}t}\mathit{\hspace{1em}\hspace{1em}}\frac{\mathrm{d}E}{\mathrm{d}x}=0$$ (11.21)

Como tal, $E$ também não pode depender de $x$; deverá ser função de $y$ e de $t$, e a sua derivada parcial em ordem a $y$ deverá ser igual à menos derivada parcial de $B$ em ordem a $t$.

Aplicando agora a terceira equação de Maxwell, (11.15), obtém-se,

$$\frac{\mathrm{d}B}{\mathrm{d}x}=0$$ (11.22)

E a quarta equação de Maxwell, (11.16), conduz as duas condições seguintes:

$$\frac{\mathrm{d}B}{\mathrm{d}y}=-\frac{1}{c^2}\frac{\mathrm{d}E}{\mathrm{d}t}\mathit{\hspace{1em}\hspace{1em}}\frac{\mathrm{d}B}{\mathrm{d}z}=0$$ (11.23)

As equações (11.22) e (11.23) implicam que $B$ depende apenas de $y$ e de $t$ e a sua derivada parcial em ordem a $y$ é igual a menos a derivada parcial de $E$ em ordem a $t$, dividida por $c^2$.

Derivando a primeira equação em (11.21) em ordem a $t$ e a primeira equação em (11.23) em ordem a $y$ e comparando os resultados, obtém-se a seguinte equação para $E$:

$$\frac{{\partial }^{2}E}{\partial t^2}=c^2\frac{{\partial }^{2}E}{\partial y^2}$$ (11.24)

E derivando a primeira equação em (11.21) em ordem a $y$ e a primeira equação em (11.23) em ordem a $t$ e comparando os resultados, obtém-se o mesmo tipo de equação para $B$:

$$\frac{{\partial }^{2}B}{\partial t^2}=c^2\frac{{\partial }^{2}B}{\partial y^2}$$ (11.25)

A equação diferencial (11.24) (ou (11.25)) é chamada equação de onda e as suas soluções são ondas progressivas que se propagam com velocidade constante, neste caso velocidade de valor $c$ na direção do eixo $z$.

Resumindo, existem soluções das equações de Maxwell no vácuo em que os campos elétrico e magnético apontam em direções fixas e perpendiculares entre si. Soluções essas que correspondem a ondas eletromagnéticas que se propagam na direção perpendicular aos campos $\overrightarrow{E}$ e $\overrightarrow{B}$. Escolhendo o eixo $z$ na direção de propagação da onda, os campos dependerão terão apenas de $z$ e de $t$ e podem ser quaisquer soluções das equações de onda (11.24) e (11.25).

Este tipo de ondas eletromagnéticas que temos descrito nesta secção é designada de onda plana polarizada. A direção de polarização de uma onda eletromagnética é definida como a direção do campo elétrico. O versor na direção do campo elétrico é o versor de polarização.

11.4 Soluções da equação de onda

A equação de onda já tinha sido amplamente estudada nos séculos anteriores à descoberta de Maxwell das ondas eletromagnéticas e têm sido usados vários métodos diferentes para obter as soluções. Explicaremos aqui o método das caraterísticas. Resolver a equação (11.24), para a componente do campo elétrico na direção de polarização, consiste em encontrar uma função $E(y,t)$ contínua, tal que a sua segunda derivada parcial em ordem a $y$ é igual à sua segunda derivada parcial em ordem a $t$ dividida por $c^2$, quaisquer que sejam os valores de $y$ e de $t$.

Substituem-se as duas variáveis $y$ e $t$ por duas novas variáveis $\zeta$ e $\eta$ definidas da forma seguinte:

$$\zeta =y+ct\mathit{\hspace{1em}\hspace{1em}}\eta =y-ct$$ (11.26)

A derivada parcial de $E$ em ordem a $t$ calculam-se usando a regra de derivação de funções compostas:

$$\frac{\partial E}{\partial t}=\frac{\partial E}{\partial \zeta }\frac{\partial \zeta }{\partial t}+\frac{\partial E}{\partial \eta }\frac{\partial \eta }{\partial t}=c\frac{\partial E}{\partial \zeta }-c\frac{\partial E}{\partial \eta }$$ (11.27)

e derivando uma segunda vez em ordem a $t$ obtém-se,

$$\frac{{\partial }^{2}E}{\partial t^2}=c^2\frac{{\partial }^{2}E}{\partial {\zeta }^2}-2c^2\frac{{\partial }^{2}E}{\partial \zeta \partial \eta }+c^2\frac{{\partial }^{2}E}{\partial {\eta }^2}$$ (11.28)

Usando o mesmo procedimento, encontra-se a segunda derivada parcial de $E$ em ordem a $y$:

$$\frac{{\partial }^{2}E}{\partial y^2}=\frac{{\partial }^{2}E}{\partial {\zeta }^2}-2\frac{{\partial }^{2}E}{\partial \zeta \partial \eta }+\frac{{\partial }^{2}E}{\partial {\eta }^2}$$ (11.29)

Substituindo as expressões (11.28) e (11.29) na equação de onda 11.24, obtém-se a seguinte equação:

$$\frac{{\partial }^{2}E}{\partial \zeta \partial \eta }=0$$ (11.30)

Para que a equação anterior seja válida, é necessário e suficiente que uma das duas derivadas parciais de $E$, em ordem a $\zeta$ ou $\eta$, seja nula. Ou seja, o campo $E$ deve ser uma função $f(\zeta )$ que depende apenas de $\zeta$, fazendo com que a sua derivada parcial em ordem a $\eta$ seja nula, ou uma função $g(\eta )$ que depende apenas de $\eta$, com derivada parcial em ordem a $\zeta$ nula. Em função das variáveis originais $y$ e $t$, os dois tipos de soluções são as seguintes:

$$E=f(y+ct)\mathit{\hspace{1em}\hspace{1em}}E=f(y-ct)$$ (11.31)

ou qualquer combinação linear desses dois tipos de soluções, porque a equação de onda é linear (ver problema 11.11.8). Uma função com alguma das formas em (11.31) denomina-se função de onda. Qualquer função contínua de uma variável conduz a uma função de onda, se a variável for substituída por $y\pm ct$.

Para cada valor de $t$, a função $f(y+ct)$ é idêntica à função $f(y)$, em $t=0$, mas deslocada no sentido negativo do eixo $y$ de uma distância igual a $ct$. Como tal, a função $E=f(y+ct)$ descreve uma onda que se propaga no sentido negativo do eixo $y$, com velocidade $c$. Uma análise semelhante mostra que $E=f(y-ct)$ descreve uma onda que se propaga no sentido positivo do eixo $y$ com velocidade $c$.

Já o campo magnético $B$, que também verifica a equação de onda, deve então ter uma forma semelhante às da equação (11.31), mas não pode ser independente da solução obtida para $E$, devido às relações (11.21) e (11.23). Substituindo as soluções (11.31) na equação (11.23), obtêm-se as respetivas soluções do campo magnético:

$$B=-\frac{1}{c}f(y+ct)\mathit{\hspace{1em}\hspace{1em}}B=\frac{1}{c}f(y-ct)$$ (11.32)

O fator $c$ no denominador implica que a intensidade do campo magnético numa onda eletromagnética é muito menor que a intensidade do campo elétrico. Os sinais obtidos nestas expressões para $B$ indicam que os campos $\overrightarrow{E}=E\hat{k}$ e $\overrightarrow{B}=B\hat{ı}$ correspondem a uma onda que se propaga no sentido positivo do eixo $y$, se em para quaisquer valores de $y$ e $t$ as duas funções $E$ e $B$ têm o mesmo sinal, ou no sentido negativo do eixo $y$ se $E$ e $B$ têm sinais opostos. O resultado anterior resume-se dizendo que a direção e o sentido de propagação da onda plana é sempre a direção e o sentido do produto vetorial $\overrightarrow{E}\times \overrightarrow{B}$, ou seja, o versor do campo elétrico $\hat{E}$ e o versor do campo magnético $\hat{B}$ satisfazem a seguinte relação:

$$\hat{E}\times \hat{B}=\hat{c}$$ (11.33)

onde $\hat{c}$ é o versor com a direção e o sentido de propagação da onda, sendo o vector velocidade da onda dado por $\overrightarrow{c}=c\hat{c}$.

Note-se que a relação dada pela expressão (11.33) pode também ser escrita como $\hat{c}\times \hat{E}=\hat{B}$ ou como $\hat{B}\times \hat{c}=\hat{E}$ (ver, por exemplo, a figura 11.6).

Conclui-se que existem duas famílias de soluções das equações de onda eletromagnética. A primeira família corresponde a ondas que se propagam no sentido positivo do eixo dos $y$ com campos elétrico e magnético dados pelas seguintes expressões:

$\overrightarrow{E}$ $=f(y-ct)\hat{k}$ (11.34)

$\overrightarrow{B}$ $={\displaystyle \frac{1}{c}}f(y-ct)\hat{ı}$ (11.35)

em que $g$ pode ser qualquer função contínua de uma variável. A figura 11.6 mostra uma dessas soluções.

Figura 11.6: Onda eletromagnética plana polarizada, com velocidade no sentido positivo do eixo $y$.

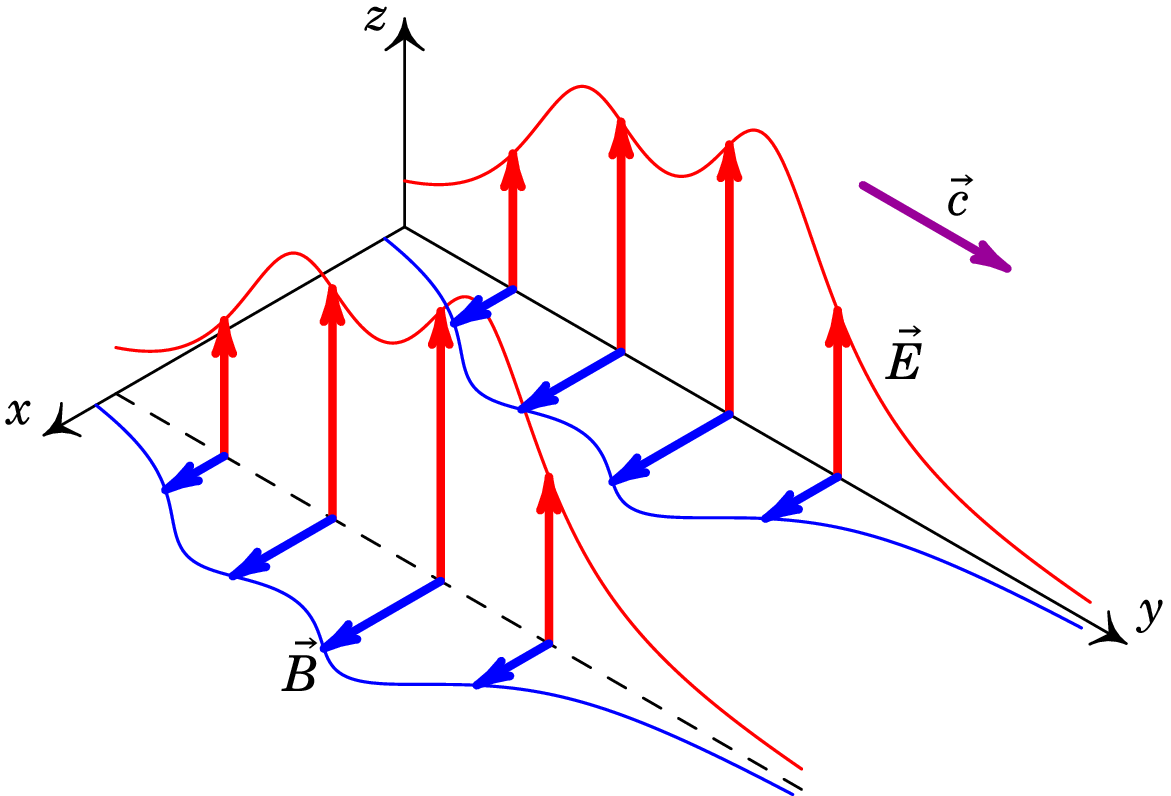
A segunda família de soluções são ondas eletromagnéticas que se propagam no sentido negativo do eixo dos $y$, e com campos que verificam as expressões:

$\overrightarrow{E}$ $=f(y+ct)\hat{k}$ (11.36)

$\overrightarrow{B}$ $=-{\displaystyle \frac{1}{c}}f(y+ct)\hat{ı}$ (11.37)

onde $f$ é qualquer função contínua de uma variável.

As ondas planas polarizadas, que se propagam na direção dos eixos $x$ ou $z$, têm formas semelhantes às equações 11.34 ou 11.36, com $y$ substituído pela coordenada correspondente à direção de propagação, o versor $\hat{k}$ substituído pelo versor na direção de polarização e $\hat{ı}$ substituído pelo versor perpendicular às direções de propagação e de polarização, seguindo a regra da mão direita do versor de propagação para o versor de polarização (equação (11.33)).

11.5 Ondas harmónicas

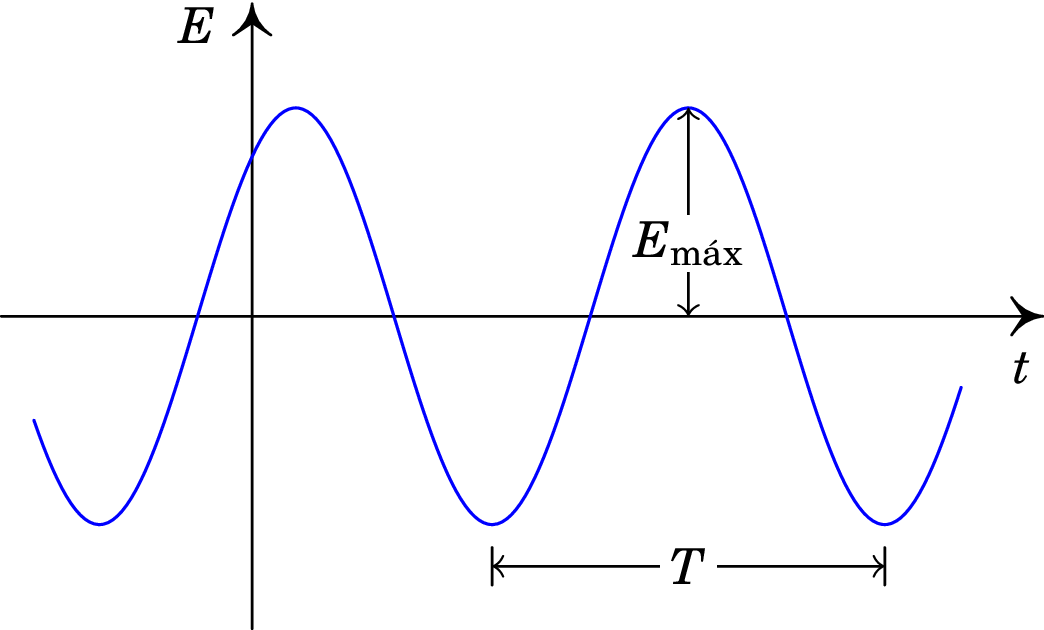
Um caso importante das ondas eletromagnéticas são as ondas periódicas que se repetem durante um intervalo de tempo. Qualquer função periódica pode ser representada como uma série de funções seno e cosseno com diferentes frequências. Quando a função de onda $f(x\pm ct)$ é uma função seno ou cosseno, a respetiva onda é chamada onda harmónica ou monocromática. Como vimos na secção LABEL:sec:sinusoidal, as funções sinusoidais são caraterizadas por três parámetros. No caso do campo elétrico de uma onda que se propaga na direção do eixo $x$, a função é da forma,

$$E(x,t)=E_{\text{máx}}\cos \left(k(x\pm ct)+\phi \right)$$ (11.38)

em que os 3 parámetros são a amplitude $E_{\text{máx}}$, o numero de onda angular, $k$, e o ângulo de fase, $\phi$. A mesma função pode escrever-se como função seno, subtraindo $\pi /2$ ao ângulo de fase. E mudando o instante em que arbitramos $t=0$, ou a posição $x$ da origem, é sempre possível fazer com que o ângulo de fase seja nulo; como tal, vamos admitir $\phi =0$.

Num instante $t$ dado a função de onda harmónica do campo eléctrico é $E_{\text{máx}}\cos (kx+\text{constante})$, que corresponde ao gráfico da figura 11.7.

Figura 11.7: Função de onda do campo elétrico em função da posição, num instante $t$ dado.

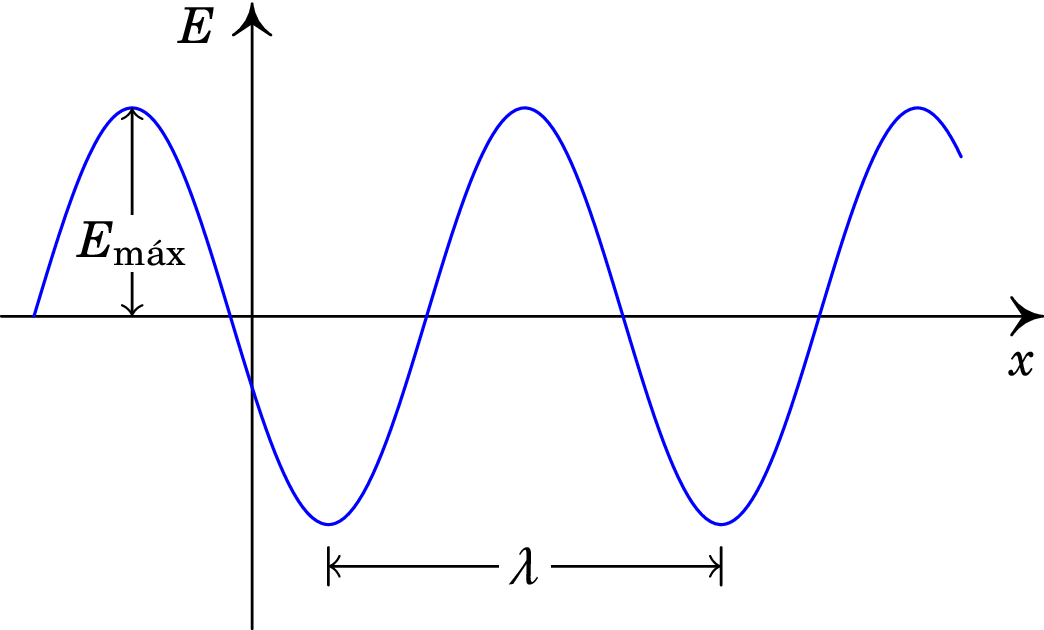
O comprimento de onda, $\lambda$, é a distância entre dois máximos ou mínimos consecutivos da onda. Ou seja, o argumento da função cosseno aumenta num fator $2\pi$ quando $x$ aumenta um comprimento de onda $\lambda$:

$$k\lambda =2\pi \mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}k=\frac{2\pi }{\lambda }$$ (11.39)

Numa posição $x$ fixa, a função de onda harmónica do campo elétrico é $E_{\text{máx}}\cos (kct+\text{constante})$, representada na figura 11.8 em função do tempo $t$.

Figura 11.8: Função de onda do campo elétrico em função do tempo, numa posição $x$ fixa.

O tempo que demora para $E$ variar entre dois valores máximos ou mínimos consecutivos é o período, $T$, da onda. Quando $t$ aumenta num período, o argumento da função cosseno varia em $2\pi$, o que conduz à seguinte relação:

$$kcT=2\pi \mathit{\hspace{1em}}⟹\mathit{\hspace{1em}}kc=\omega$$ (11.40)

onde a frequência angular, $\omega$ é igual a,

$$\omega =\frac{2\pi }{T}=2\pi f$$ (11.41)

e $f$ é a frequência igual ao inverso do período.

Como veremos, a amplitude $E_{\text{máx}}$ está relacionada com a intensidade da onda. A onda é caraterizada apenas por uma das quatro constantes, $f$, $\lambda$, $\omega$ e $k$. Dada uma dessas constantes, as outras três podem ser calculadas com as equações (11.39), (11.40) e (11.41).

Se a onda se propaga no sentido positivo do eixo $x$, a função de onda do campo elétrico é,

$$E(x,t)=E_{\text{máx}}\cos (kx-\omega t)$$ (11.42)

e se a propagação é no sentido negativo do eixo $x$, a função de onda é,

$$E(x,t)=E_{\text{máx}}\cos (kx+\omega t)$$ (11.43)

Podem existir ondas harmónicas planas propagando-se em qualquer outra direção diferente do eixo $x$. Nesses casos, nas equações (11.42) e (11.43) $x$ é substituída pela variável na direção em que a onda se propaga.

Numa onda plana com polarização linear, a direção do campo é constante em todo o espaço e o versor nessa direção designa-se versor de polarização. No caso das ondas propagando-se na direção do eixo $x$, o versor de polarização terá de ser perpendicular ao eixo $x$ e pode ser escrito como:

$$\cos \theta \hat{ȷ}+\sin \theta \hat{k}$$ (11.44)

A função de onda do campo magnético é a mesma função de onda do campo elétrico, dividida por $c$, e o versor na direção do campo magnético deverá estar também no plano perpendicular a versor na direção de propagação da onda, perpendicular ao vetor de polarização e de forma que o produto vetorial do vetor de polarização pelo versor do campo magnético seja o versor com a direção e sentido de propagação da onda.

Concluindo as expressões dos campos de uma onda harmónica com polarização linear, que se propaga no sentido positivo do eixo $x$ são as seguintes:

$\overrightarrow{E}$ $=E_{\text{máx}}\cos (kx-\omega t)(\cos \theta \hat{ȷ}+\sin \theta \hat{k})$ (11.45)

$\overrightarrow{B}$ $={\displaystyle \frac{E_{\text{máx}}}{c}}\cos (kx-\omega t)(-\sin \theta \hat{ȷ}+\cos \theta \hat{k})$ (11.46)

e se a onda se propaga na sentido negativo do eixo $x$, as expressões dos campos são as seguintes:

$\overrightarrow{E}$ $=E_{\text{máx}}\cos (kx+\omega t)(\cos \theta \hat{ȷ}+\sin \theta \hat{k})$ (11.47)

$\overrightarrow{B}$ $={\displaystyle \frac{E_{\text{máx}}}{c}}\cos (kx+\omega t)(\sin \theta \hat{ȷ}+-\cos \theta \hat{k})$ (11.48)

A sobreposição de duas ondas planas origina uma outra onda eletromagnética plana, já que a equação de onda é linear (ver problema 11.11.8). A sobreposição de ondas harmónicas planas, permite “construir” ondas planas mais complicadas, que não são necessariamente harmónicas. E qualquer onda periódica pode ser obtida como sobreposição de ondas harmónicas, por meio da série de Fourier.

Exemplo 11.2

A seguinte sobreposição de duas ondas harmónicas polarizadas linearmente, com a mesma frequência,

$$\overrightarrow{E}=E_{\text{máx}}\left[\cos (kx-\omega t)\hat{ȷ}+\sin (kx-\omega t)\hat{k}\right]$$

denomina-se onda com polarização circular. Mostre que em diferentes pontos do espaço e em diferentes instantes o módulo do campo $\overrightarrow{E}$ é sempre o mesmo, mas a direção de $\overrightarrow{E}$ num ponto dado roda em função do tempo e num instante dado roda também em função da posição $x$.

Resolução. O módulo do campo é,

$$|\overrightarrow{E}|=E_{\text{máx}}\sqrt{{\cos }^2(kx-\omega t)+{\sin }^2(kx-\omega t)}=E_{\text{máx}}$$

ou seja, em qualquer posição e em qualquer instante o módulo do campo elétrico é sempre o mesmo, $E_{\text{máx}}$.

E o ângulo que o campo $\overrightarrow{E}$ faz com o semieixo positivo $y$, no plano $yz$, é igual a,

$$\theta ={\tan }^{-1}\left(\frac{E_z}{E_y}\right)={\tan }^{-1}\left[\tan (kx-\omega t)\right]=kx-\omega t$$

As derivadas de $\theta$ são,

$$\frac{\partial \theta }{\partial x}=k\mathit{\hspace{1em}\hspace{1em}}\frac{\partial \theta }{\partial t}=-\omega$$

Isso implica que num instante $t$ dado, a direção do campo $\overrightarrow{E}$ roda no sentido positivo (de $y$ para $z$) quando $x$ aumenta (ver figura 11.9). E num ponto fixo, por exemplo, a origem no caso da figura 11.9, $\overrightarrow{E}$ roda no sentido negativo (de $z$ para $y$) em função do tempo.

Como neste caso a onda propaga-se no sentido positivo do eixo $x$, a rotação de $\overrightarrow{E}$ em função de $x$ é no sentido da regra da mão direita em relação ao sentido de propagação da onda e diz-se que a onda tem polarização circular direita ou positiva.

Figura 11.9: Onda eletromagnética com polarização circular direita.

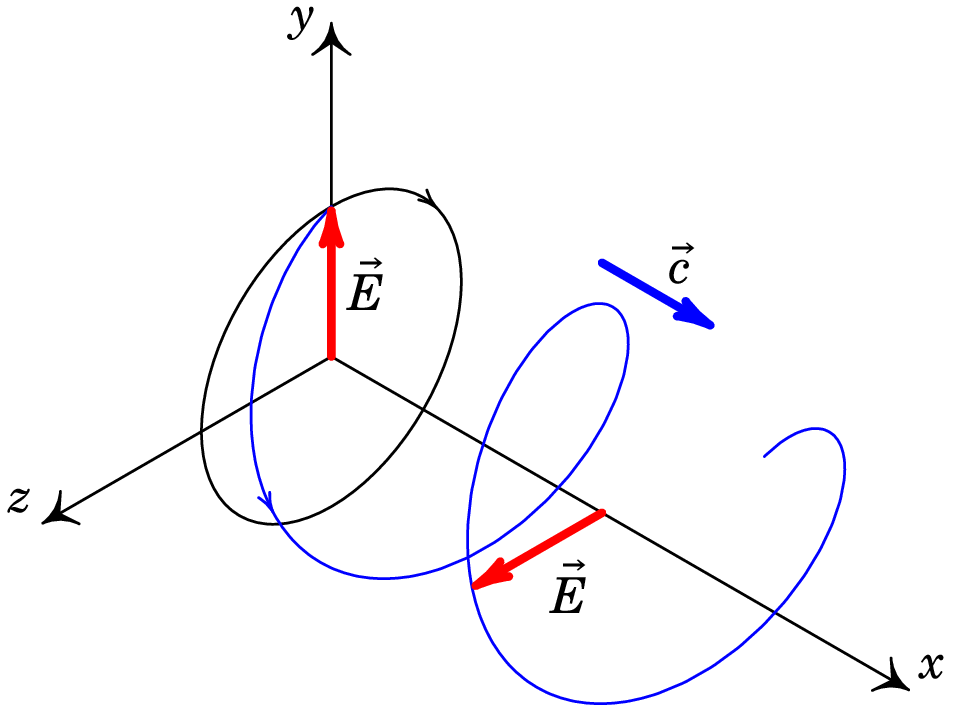
Como ilustra o exemplo anterior, a sobreposição de duas ondas planas da mesma frequência e amplitude, com diferença de fase de $\pm \pi /2$ e polarizadas em direções perpendiculares, produz ondas com polarização circular direita ou esquerda (positiva ou negativa) segundo o campo elétrico rode no sentido da regra da mão direita, em relação ao sentido de propagação, ou no sentido oposto.

Exemplo 11.3

O campo elétrico,

$$\overrightarrow{E}=E_{\text{máx}}\sin (kx)\cos (\omega t)\hat{ȷ}$$ (11.49)

onde $k/\omega =c$, descreve uma onda eletromagnética estacionária, na qual os pontos onde o campo é máximo, mínimo ou nulo permanecem fixos. Demonstre que a onda estacionária é solução da equação de onda e pode ser obtida a partir da sobreposição de duas ondas harmónicas planas, com a mesma frequência, propagando-se na mesma direção mas em sentidos opostos.

Resolução. As derivadas parciais da componente $y$ do campo são as seguintes:

${\displaystyle \frac{\partial E}{\partial x}}=E_{\text{máx}}k\cos (kx)\cos (\omega t)$

${\displaystyle \frac{{\partial }^{2}E}{\partial x^2}}=-E_{\text{máx}}{k}^2\sin (kx)\cos (\omega t)=-k^{2}E$

${\displaystyle \frac{\partial E}{\partial t}}=-E_{\text{máx}}\omega \sin (kx)\sin (\omega t)$

${\displaystyle \frac{{\partial }^{2}E}{\partial t^2}}=-E_{\text{máx}}{\omega }^2\sin (kx)\cos (\omega t)=-{\omega }^{2}E$

e como $k/\omega =c$, o campo $\overrightarrow{E}$ é solução da equação de onda plana:

$$\frac{{\partial }^{2}E}{\partial x^2}=\frac{1}{c^2}\frac{{\partial }^{2}E}{\partial t^2}$$

Para decompor a onda estacionária em ondas planas, usa-se a identidade trigonométrica

$$\sin (kx)\cos (\omega t)=\frac{1}{2}\left[\sin (kx+\omega t)+\sin (kx-\omega t)\right]$$

que conduz a,

$$\overrightarrow{E}=\frac{E_{\text{máx}}}{2}\sin (kx+\omega t)\hat{ȷ}+\frac{E_{\text{máx}}}{2}\sin (kx-\omega t)\hat{ȷ}$$

Os dois termos nesta última expressão correspondem a ondas harmónicas, polarizadas na direção $\hat{ȷ}$, com a mesma frequência $f=\omega /2\pi$, que se propagam em direções opostas.

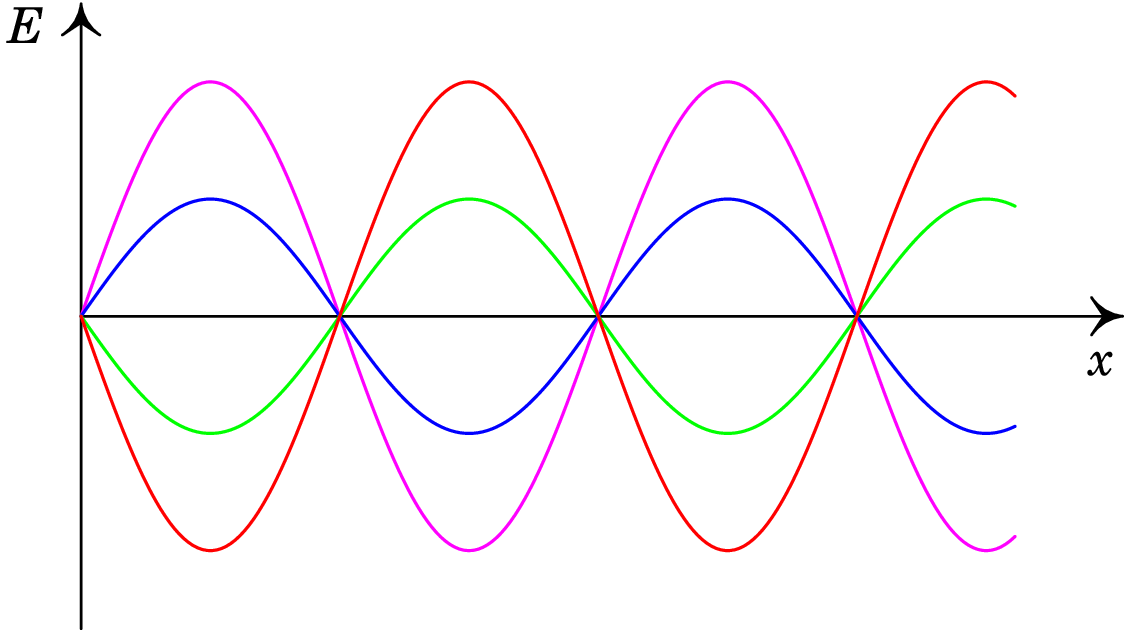
A figura 11.10 mostra a função de onda $E$ da onda estacionária do exemplo anterior, em diferentes instantes, em função de $x$. Há pontos, designados de nós, onde o campo é sempre nulo e nos outros pontos o campo oscila com diferentes amplitudes, $E_{\text{máx}}\sin (kx)$.

Figura 11.10: Onda eletromagnética estacionária.

11.6 Equação vetorial de onda eletromagnética

A equação de onda eletromagnética plana (11.24) foi obtida arbitrando uma direções constantes para os campos $\overrightarrow{E}$ e $\overrightarrow{B}$. Para obter uma forma mais geral da equação de onda, começaremos por calcular o rotacional nos dois lados da equação (11.14):

$$\overrightarrow{\nabla }\times (\overrightarrow{\nabla }\times \overrightarrow{E})=-\overrightarrow{\nabla }\times \frac{\partial \overrightarrow{B}}{\partial t}$$ (11.50)

Usando a propriedade (A.90) do rotacional no lado esquerdo da equação e trocando as derivadas em ordem ao tempo e à posição no lado direito da equação obtém-se,

$$\overrightarrow{\nabla }(\overrightarrow{\nabla }\cdot \overrightarrow{E})-{\nabla }^2\overrightarrow{E}=-\frac{\partial }{\partial t}\overrightarrow{\nabla }\times \overrightarrow{B}$$ (11.51)

E substituindo as expressões da divergência de $\overrightarrow{E}$, equação (11.13), e do rotacional de $\overrightarrow{B}$, equação (11.16), obtém-se a forma vetorial da equação de onda eletromagnética:

$${\nabla }^2\overrightarrow{E}=\frac{1}{c^2}\frac{{\partial }^2\overrightarrow{E}}{\partial t^2}$$ (11.52)

Se em vez de começar por calcular o rotacional do rotacional de $\overrightarrow{E}$ começamos por calcular o rotacional do rotacional de $\overrightarrow{B}$ obtém-se a mesma equação de onda para o campo $\overrightarrow{B}$.

11.7 Ondas esféricas

As ondas planas são uma aproximação válida dentro de uma região pequena quando comparada com a distância à fonte das ondas, já que uma onda eletromagnética real costuma propagar-se em várias direções, e não numa direção única.

Se a fonte que produz a onda puder ser considerada uma fonte pontual, a propagação da onda será nas direções radiais com origem na fonte; assim, o vetor de polarização estará sobre a superfície esférica definida pelos versores esféricos $\hat{\theta }$ e $\hat{\varphi }$. E se a fonte é isotrópica, i.e., produz a mesma radiação em qualquer direção, as funções de onda $E$ e $B$ poderão depender unicamente da coordenada radial esférica $r$ e não das coordenadas angulares; nesse caso a onda tem simetria esférica e é designada de onda esférica.

Consideremos o caso em que o vetor $\overrightarrow{E}$ duma onda esférica está sempre na direção azimutal esférica $\hat{\varphi }$:

$$\overrightarrow{E}=E(r,t)\hat{\varphi }$$ (11.53)

Usando a expressão (A.83) do Laplaciano em coordenadas esféricas obtém-se,

$${\nabla }^{2}E\hat{\varphi }=\frac{1}{r}\frac{{\partial }^2}{\partial r^2}(rE)\hat{\varphi }$$ (11.54)

onde os termos com derivadas em ordem aos ângulos foram anulados porque $E$ não depende dos ângulos.

A equação vetorial de onda eletromagnética (11.52) implica que,

$$\frac{{\partial }^2(rE)}{\partial r^2}=\frac{1}{c^2}\frac{{\partial }^2(rE)}{\partial t^2}$$ (11.55)

Esta é a mesma equação da onda plana (11.24) mas para a função $rE$. Como tal $rE$ deverá ser uma função de onda $f(r-ct)$ que se propaga na direção radial e a função de onda do campo elétrico será:

$$E(r,t)=\frac{1}{r}f(r-ct)$$ (11.56)

Note-se que neste caso não consideramos as soluções $f(r+ct)$ porque a onda esférica estará sempre a afastar-se da fonte em $r=0$.sinal positivo corresponde a ondas que se propagam em direção à origem. Também, a fonte pontual é uma aproximação e, por isso $r$ não chega a ser exatamente igual a 0 e $E(r,t)$ não fica infinita.

As funções da forma $f(r-ct)/r$ representam uma onda que se propaga na direção radial, afastando-se da origem com velocidade $c$, mas cuja forma não permanece constante, diminuindo à medida que a onda se afasta da origem. A função de onda do campo magnético pode obter-se a partir da segunda equação de Maxwell (11.14); como admitimos campo elétrico apenas com componente $E_{\varphi }$, usando a equação (A.77) o resultado é,

$$\overrightarrow{\nabla }\times \overrightarrow{E}=-\frac{1}{r}\frac{\partial (rE)}{\partial r}\hat{\theta }=-\frac{1}{r}{f}^{\prime }(r-ct)\hat{\theta }$$ (11.57)

e como a derivada temporal de $f(r-ct)$ é igual a:

$$\frac{\partial f(r-ct)}{\partial t}=-c{f}^{\prime }(r-ct)$$ (11.58)

comparando estas duas equações com a segunda equação de Maxwell (11.14), conclui-se que a expressão do campo magnético é:

$$\overrightarrow{B}=-\frac{1}{cr}f(r-ct)\hat{\theta }$$ (11.59)

Figura 11.11: Função de onda esférica, harmónica, num instante $t$ dado.

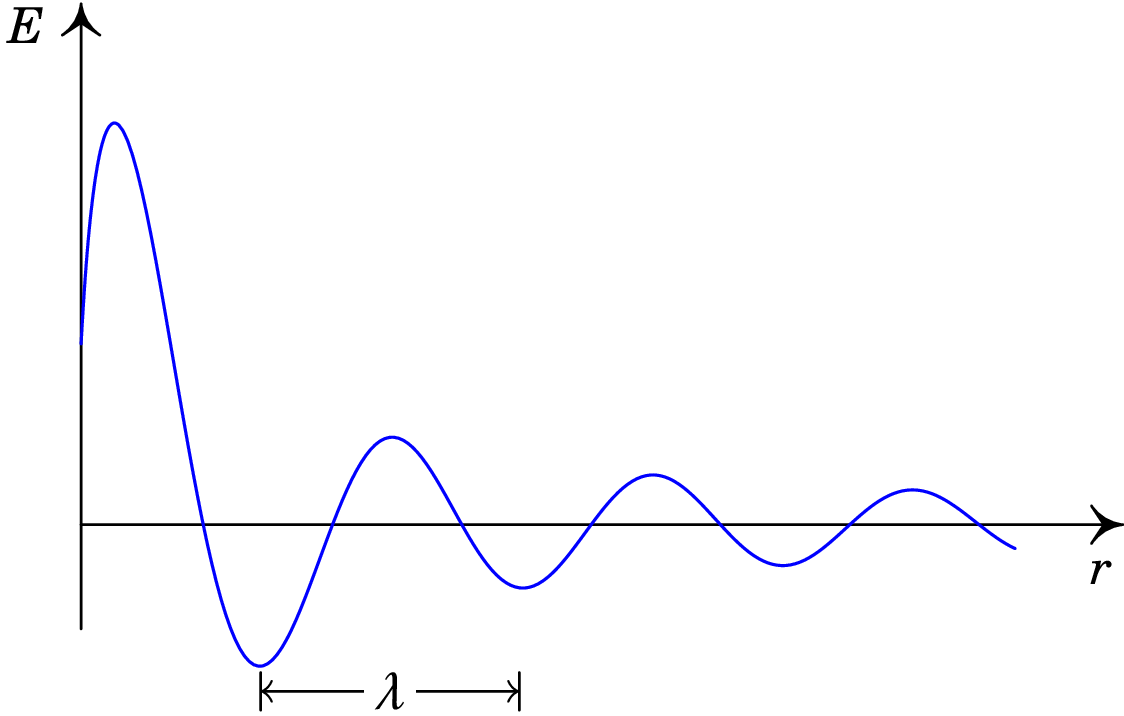
No caso de uma onda esférica monocromática (harmónica), a função de onda do campo elétrico pode ser escrita da forma (ver figura 11.11):

$$E(r,t)=\frac{{\epsilon }_0}{r}\cos (kr-\omega t)$$ (11.60)

em que a constante ${\epsilon }_0$ tem unidades de voltagem. Nos pontos à distância $r$ da fonte o campo elétrico $E$ oscila com amplitude ${\epsilon }_0/r$ e frequência $f=\omega /(2\pi )$. A pesar da diminuição da amplitude em função de $r$, as esferas onde o campo é máximo ou mínimo, chamadas frentes de onda, estão separadas por uma distância constante, igual ao comprimento de onda $\lambda =2\pi /k$ (ver figura 11.11).

11.8 Energia do campo eletromagnético

Em cada ponto do espaço onde existe campo eletromagnético e densidade de carga $\rho$, o campo produz deslocamento $\mathrm{d}\overrightarrow{r}$ dessa carga e o trabalho realizado pelo campo eletromagnético sobre a carga infinitesimal nesse ponto é,

$$\mathrm{d}W=\rho \overrightarrow{E}\cdot \mathrm{d}\overrightarrow{r}$$ (11.61)

O campo $\overrightarrow{B}$ não realiza trabalho porque a parte magnética da força é perpendicular ao deslocamento. A potência instantânea fornecida pelo campo, por unidade de volume, é igual a:

$$P=\frac{\mathrm{d}W}{\mathrm{d}t}=\rho \overrightarrow{E}\cdot \frac{\mathrm{d}\overrightarrow{r}}{\mathrm{d}t}=\overrightarrow{E}\cdot \overrightarrow{J}$$ (11.62)

E usando a quarta equação de Maxwell (11.12) para escrever a densidade de corrente em função do campo, essa potência é,

$$P=\overrightarrow{E}\cdot \left(\frac{\overrightarrow{\nabla }\times \overrightarrow{B}}{4\pi k_{\mathrm{m}}}-\frac{1}{4\pi k}\frac{\partial \overrightarrow{E}}{\partial t}\right)$$ (11.63)

A propriedade (A.91) e a segunda equação de Maxwell (11.11) conduzem a,

$\overrightarrow{E}\cdot (\overrightarrow{\nabla }\times \overrightarrow{B})$ $=\overrightarrow{B}\cdot (\overrightarrow{\nabla }\times \overrightarrow{E})-\overrightarrow{\nabla }\cdot (\overrightarrow{E}\times \overrightarrow{B})$

$=-\overrightarrow{B}\cdot {\displaystyle \frac{\partial \overrightarrow{B}}{\partial t}}-\overrightarrow{\nabla }\cdot (\overrightarrow{E}\times \overrightarrow{B})$ (11.64)

Substituindo na equação (11.63) e tendo em conta que para qualquer vetor $\overrightarrow{a}\cdot \mathrm{d}\overrightarrow{a}/\mathrm{d}t$ é igual a $(\mathrm{d}{a}^2/\mathrm{d}t)/2$, obtém-se:

$$\frac{1}{4\pi k_{\mathrm{m}}}\overrightarrow{\nabla }\cdot (\overrightarrow{E}\times \overrightarrow{B})=-\frac{\partial }{\partial t}\left(\frac{B^2}{8\pi k_{\mathrm{m}}}+\frac{E^2}{8\pi k}\right)-P$$ (11.65)

O vetor,

$$\overrightarrow{S}=\frac{1}{4\pi k_{\mathrm{m}}}\overrightarrow{E}\times \overrightarrow{B}$$ (11.66)

designa-se vetor de Poynting e o termo,

$$u=\frac{E^2}{8\pi k}+\frac{B^2}{8\pi k_{\mathrm{m}}}$$ (11.67)

é a densidade de energia do campo eletromagnético. A equação (11.65), conhecida como teorema de Poynting,

$$\overrightarrow{\nabla }\cdot \overrightarrow{S}=-\frac{\partial u}{\partial t}-P$$ (11.68)

mostra que o vetor de Poynting é a densidade direcional do fluxo de energia eletromagnética. A sua divergência num ponto é igual á diminuição de energia eletromagnética nesse ponto, por unidade de tempo, mais a energia eletromagnética convertida em energia mecânica, por unidade de tempo.

No caso das ondas eletromagnéticas no vácuo, não existem cargas e, como tal, não há potência $P$ fornecida às cargas. O fluxo de energia eletromagnética é na direção do vetor de Poynting, que é a direção de propagação da onda e o efeito desse fluxo é transferir energia eletromagnética $u$ associada ao campo eletromagnético.

Como os campos $\overrightarrow{E}$ e $\overrightarrow{B}$ numa onda eletromagnética são perpendiculares e o módulo de $\overrightarrow{B}$ é igual ao módulo de $\overrightarrow{E}$ dividido por $c$, o módulo do vetor de Poynting de uma onda eletromagnética é igual a,

$$S=\frac{c}{4\pi k}{E}^2$$ (11.69)

e costuma ser chamado também densidade do fluxo de energia da onda, porque é a energia transferida, por unidade de área e por unidade de tempo.

Se a onda for harmónica, o quadrado da função de onda $E$ é uma função do tempo e da posição; por exemplo, se a onda se propaga na direção $\hat{ı}$,

$$E^2=E_{\text{máx}}^2{\cos }^2\left(kx-\omega t\right)$$ (11.70)

que em cada posição $x$ oscila entre 0 e $E_{\text{máx}}^2$ e tem valor médio igual a $E_{\text{máx}}^2/2$. Como tal, o valor médio da densidade de fluxo de energia é:

$$S=\frac{c}{8\pi k}{E}_{\text{máx}}^2$$ (11.71)

Numa onda esférica, o fluxo total de energia fornecida pela fonte é igual à densidade do fluxo de energia, $S$, à distância $r$, multiplicado pela área da esfera de raio $r$:

$${\mathrm{\Phi }}_{\mathrm{e}}=\frac{c}{2k}{\epsilon }_0^2$$ (11.72)

As unidades de ${\mathrm{\Phi }}_{\mathrm{e}}$ são unidades de potência (energia fornecida pela fonte por unidade de tempo).

Problemas

1. Uma onda eletromagnética propaga-se no vácuo, no sentido positivo do eixo $x$. No instante $t=0$, o campo elétrico em função de $x$ é dado pela função (unidades SI)

   $$E=\frac{50}{x^2+2}$$

   Calcule o campo no ponto $x=50$ m, no instante $t=0.2$ µs.

2. Uma lâmina metálica muito extensa encontra-se sobre o plano $xy$. A lâmina é ligada a uma fonte variável que produz um campo elétrico uniforme no plano $xy$, mas variável no tempo segundo a expressão:

   $$\overrightarrow{E}=E_{\text{máx}}\sin (\omega t)\hat{ı}$$

   onde $E_{\text{máx}}$ e $\omega$ são constantes. O campo elétrico na lâmina origina uma onda eletromagnética plana. Escreva as funções que representam os campos elétrico e magnético da dita onda, em função do tempo e da posição.

3. Considere um condensador de armaduras circulares de raio $1\mathrm{cm}$, paralelas e planas, separadas por $1\mathrm{mm}$ de ar. Num determinado instante, a corrente no condensador é 5 A.
   (a) Calcule a derivada do campo elétrico entre as placas, em ordem ao tempo, nesse instante.
   (b) Mostre que a corrente de deslocamento entre as placas é igual à corrente de 5 A.
   (c) Porque razão as duas correntes são iguais?

4. Uma onda harmónica plana, polarizada, com $\lambda =3\mathrm{m}$, propaga-se na direção do versor $\hat{ȷ}$. Escreva as equações dos campos elétrico e magnético, nos seguintes casos:
   (a) A onda está polarizada linearmente, com versor de polarização $(\hat{ı}+\hat{k})/\sqrt{2}$.
   (b) A onda está polarizada linearmente, com versor de polarização $(\hat{ı}+\sqrt{3}\hat{k})/2$.
   ($c$) A onda tem polarização circular negativa.

5. Uma estação de rádio transmite na frequência de $90.8$ MHz. Calcule o comprimento de onda, frequência angular e número de onda angular dessas ondas de rádio com $90.8$ MHz.

6. O fluxo de energia de uma onda eletromagnética esférica e monocromática é 100 W.
   (a) Calcule a densidade do fluxo de energia a 2 m do centro da onda.
   (b) Determine os valores máximos dos campos $\overrightarrow{E}$ e $\overrightarrow{B}$ a 2 m do centro da onda.

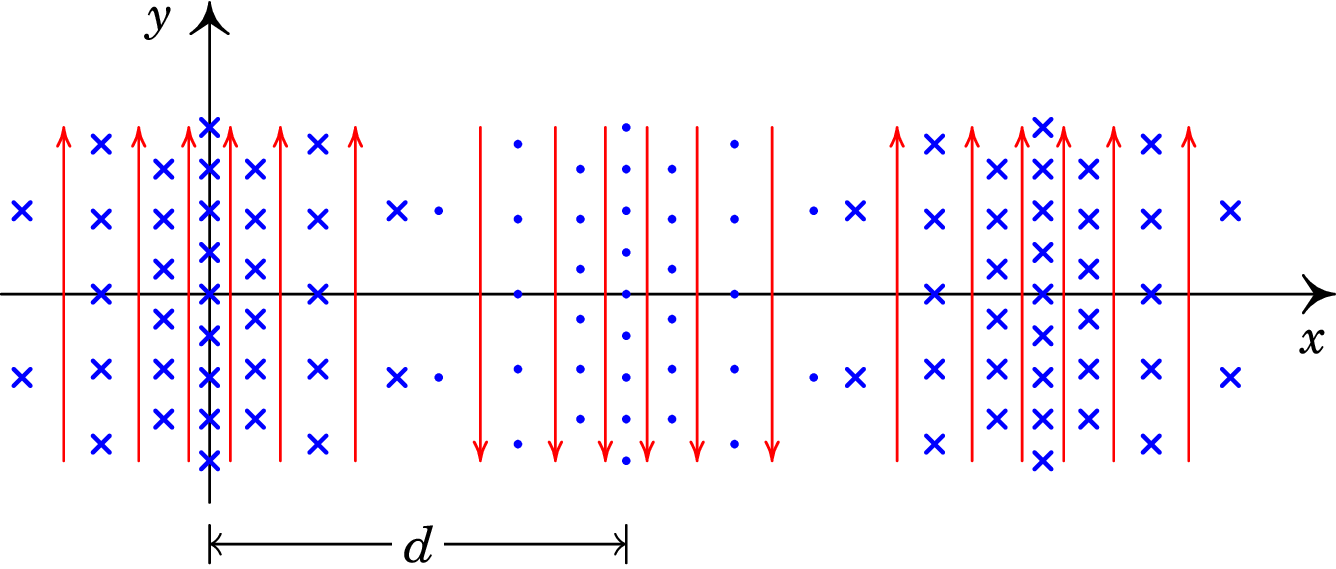
7. A figura seguinte representa o campo eletromagnético de uma onda plana de 420 MHz, no instante $t=0$. As linhas de campo verticais representam o campo elétrico e as linhas perpendiculares à folha de papel são as linhas de campo magnético. Calcule a distância $d$ e determine a expressão do vetor do campo magnético em função do tempo e da coordenada $x$.

   

8. Demonstre que a equação de onda é linear, ou seja, que qualquer combinação linear de duas soluções é também solução.

9. Considere uma onda eletromagnética plana, polarizada linearmente na direção do eixo $x$, que se propaga na direção positiva do eixo $y$. A sua frequência é de 12 MHz e a sua amplitude é $E_{\text{máx}}=\mathrm{0,008}$ V/m.
   (a) Calcule o período e o comprimento de onda.
   (b) Escreva as funções de onda dos campos $\overrightarrow{E}$ e $\overrightarrow{B}$.

10. As órbitas de Marte e da Terra estão, aproximadamente, sobre o mesmo plano. A distância média de Marte ao Sol é de 229 Gm e a distância média da Terra ao Sol é de 150 Gm. Suponha que está em comunicação com um astronauta em órbita à volta de Marte. Se o tempo médio de resposta do astronauta às suas mensagens for $t_1$, quando a Terra está entre o Sol e Marte e $t_2$ quando o Sol está entre a Terra e Marte, calcule $\mathrm{\Delta }t=t_2-t_1$.

11. Uma onda eletromagnética plana propaga-se no sentido negativo do eixo dos $y$. Num dado instante $t=0$ o campo elétrico é $\overrightarrow{E}=E_{\text{máx}}\sin (\mathrm{2,.25}\times {10}^{7}y)\hat{k}$, onde $y$ é medido em metros.
    (a) Calcule o comprimento de onda.
    (b) Calcule a frequência.
    (c) Diga qual é o versor de polarização.

12. O campo elétrico de uma onda estacionária no vácuo é dado pela função:

    $$\overrightarrow{E}=E_{\text{máx}}\cos (ky)\cos (\omega t)\hat{ı}$$

    
    

    (a) Calcule o campo magnético.
    (b) Encontre o vetor de Poynting em qualquer ponto e em qualquer instante.
    (c) Calcule a densidade média de fluxo energético, $\varphi$, em qualquer ponto.

13. Calcule o rotacional e a divergência dos campos (11.45) e (11.46) da onda plana com polarização linear e mostre que verificam as quatro equações de Maxwell no vácuo, (11.13), (11.14), (11.15) e (11.16).

Respostas

1. $0.4902$ V/m.

3. (a) ${\displaystyle \frac{\mathrm{d}E}{\mathrm{d}t}}={\displaystyle \frac{4kI}{r^2}}=1.8\times {10}^{15}$ V/(m·s). (b) $I_{\mathrm{d}}={\displaystyle \frac{r^2}{4k}}{\displaystyle \frac{\mathrm{d}E}{\mathrm{d}t}}$ e substituindo a expressão de ${\displaystyle \frac{\mathrm{d}E}{\mathrm{d}t}}$ da alínea anterior conclui-se que $I_{\mathrm{d}}=I$. (c) Considerando uma curva fechada C que envolve o condensador, paralela às armaduras, para que o integral de linha de $\overrightarrow{B}$ ao longo dessa curva seja contínuo fora das armaduras e entre elas, a som $I_{\mathrm{C}}+I_{\mathrm{d}}$ deve ser constante e, como fora das armaduras $I_{\mathrm{C}}=I$ e $I_{\mathrm{d}}=0$, entre as armaduras $I_{\mathrm{C}}=0$ e $I_{\mathrm{d}}$ deverá ser igual a $I$.

4. Arbitrando constante de fase inicial nula:
   (a) $\overrightarrow{E}={\displaystyle \frac{E_{\text{máx}}}{\sqrt{2}}}\cos (ky-\omega t)(\hat{ı}+\hat{k})$
        $\overrightarrow{B}={\displaystyle \frac{E_{\text{máx}}}{\sqrt{2}c}}cos(ky-\omega t)(\hat{ı}-\hat{k})$
   (b) $\overrightarrow{E}={\displaystyle \frac{E_{\text{máx}}}{2}}\cos (ky-\omega t)(\hat{ı}+\sqrt{3}\hat{k})$
        $\overrightarrow{B}={\displaystyle \frac{E_{\text{máx}}}{2c}}\cos (ky-\omega t)(\sqrt{3}\hat{ı}-\hat{k})$
   (c) $\overrightarrow{E}=E_{\text{máx}}\left[\cos (ky-\omega t)\hat{ı}+\sin (ky-\omega t)\hat{k}\right]$
        $\overrightarrow{B}={\displaystyle \frac{E_{\text{máx}}}{2c}}\left[\sin (ky-\omega t)\hat{ı}-\cos (ky-\omega t)\hat{k}\right]$
   onde $k=2.094$ rad/m e $\omega =6.279\times {10}^8$ rad/s.

5. 3.30 m, $5.71\times {10}^8$ rad/s, 1.90 rad/m.

6. (a) $1.989$ W/m${}^2$. (b) $E_{\text{máx}}=38.7$ N/C, $B_{\text{máx}}=1.29$ mG.

7. $d=35.71$ cm, $B=B_{\text{máx}}\cos \left(8.80x+2.64\times {10}^{9}t\right)$ ($t$ em segundos e $x$ em metros).

8. Calculam-se as derivadas parciais duma combinação linear $E=a_1{E}_1+a_2{E}_2$, onde $a_1$ e $a_2$ são constantes, e se $E_1$ e $E_2$ são soluções da equação de onda, obtém-se ${\partial }^{2}E/\partial x^2$ igual a ${\partial }^{2}E/\partial t^2$ dividida por $c^2$ e, como tal, a combinação linear $E$ também é solução.

9. (a) $T=83.33\mathrm{ns}$, $\lambda =25\mathrm{m}$.
   (b) $\overrightarrow{E}=0.008\cos (0.2513y-75.40\times {10}^{6}t+{\phi }_0)\hat{ı}$,
   (b) $\overrightarrow{B}=-2.67\times {10}^{-11}\cos (0.2513y-75.40\times {10}^{6}t)\hat{k}$ (unidades SI).

10. 2000 s (33.3 minutos).

11. (a) 279 nm. (b) $1.074\times {10}^{15}$ Hz. (c) O versor $\hat{k}$.

12. (a) $\overrightarrow{B}=-{\displaystyle \frac{E_{\text{máx}}}{c}}\sin (ky)\sin (\omega t)\hat{k}$.
    (b) $\overrightarrow{S}={\displaystyle \frac{c{ϵ}_0{E}_{\text{máx}}^2}{4}}\sin (2ky)\sin (2\omega t)\hat{ȷ}$.
    (c) 0.