9. Indução eletromagnética

Michael Faraday (1791–1867)
Em 1820, após a descoberta de Ørsted (1777–1851), que a corrente elétrica produz campo magnético, muitos investigadores tentaram produzir o efeito inverso: produzir corrente elétrica usando campos magnéticos. Joseph Henry (1797–1878) e, de forma independente, Michael Faraday, mostraram que era possível produzir corrente elétrica usando campo magnético variável ou condutores em movimento dentro dum campo magnético estático. Quando em 1831 Faraday publicou os seus resultados, o trabalho de Henry era ainda desconhecido. Como tal, a descoberta desse fenómeno (indução eletromagnética) é atribuída a Faraday.
9.1 Campo elétrico induzido
A força sobre uma partícula de carga numa região onde existem campos elétrico e magnético é dada pela força de Lorentz, expressão (7.5):
| (9.1) |
A força de Lorentz possui duas componentes, uma elétrica e outra magnética. Uma vez que a aceleração é igual em todos os referenciais inerciais, a força de Lorentz deverá conduzir ao mesmo resultado em qualquer referencial inercial. Isto é possível porque os campos elétrico e magnético têm diferentes valores em diferentes referenciais. É portanto mais correto considerar que existe um campo eletromagnético, igual em qualquer referencial, mas com componentes elétrica e magnética que podem ser diferentes em diferentes referenciais.
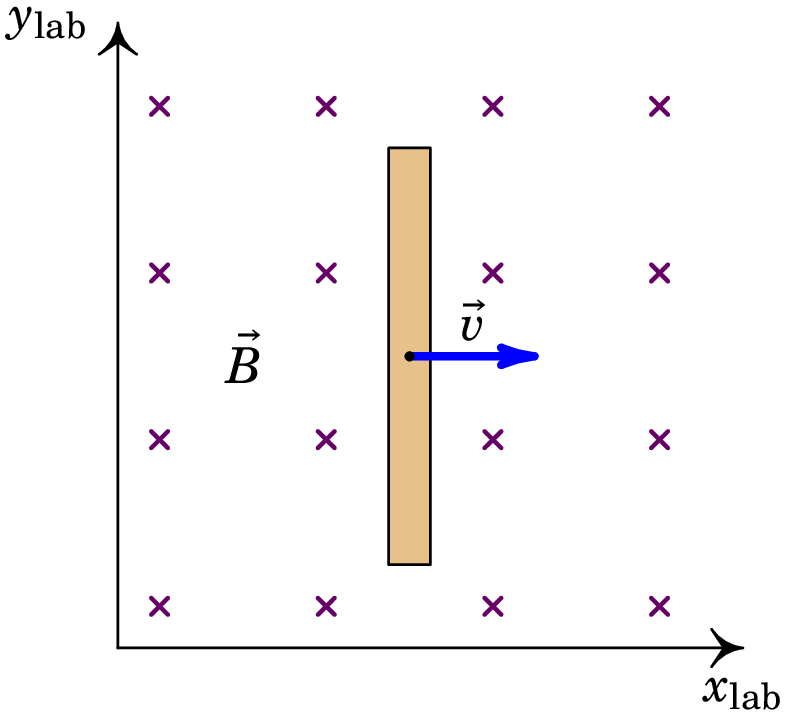
Consideremos uma barra condutora em movimento numa região onde existe campo magnético uniforme, , como na figura 9.1 e que não existe campo elétrico.
No referencial do laboratório, (, ), no qual o campo é estático e o condutor está em movimento, a força de Lorentz sobre cada partícula com carga no condutor é igual a:
| (9.2) |
sendo devida unicamente à sua componente magnética.
Já no referencial (, ) fixo ao condutor (ver figura 9.2), a velocidade do condutor é nula, mas o campo magnético não é estático, uma vez que o referencial do laboratório tem velocidade relativamente ao referencial fixo ao condutor.
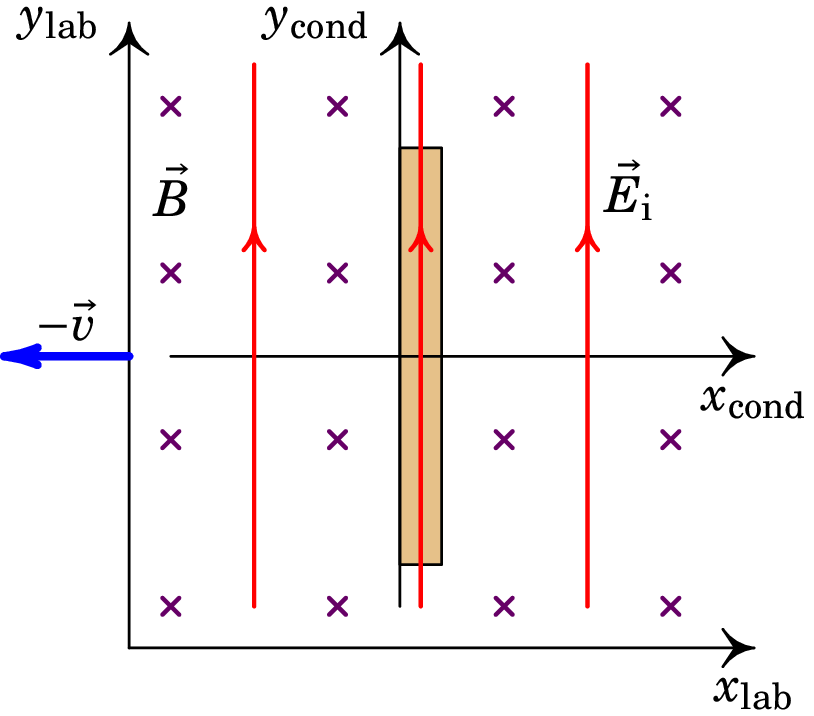
O movimento das linhas de campo magnético, no referencial do condutor, induz um campo elétrico neste referencial, dito campo elétrico induzido, dado pela expressão:
| (9.3) |
No referencial do condutor, a força de Lorentz conduz à mesma força que no referencial do laboratório (expressão (9.2)),
| (9.4) |
sendo agora devida exclusivamente à sua componente elétrica. Neste referencial, para além do campo elétrico induzido , existe também o campo magnético , uniforme mas não-estático. Contudo, a componente magnética da força de Lorentz é nula porque o condutor está em repouso.
Num terceiro referencial, com velocidade em relação ao referencial do laboratório ( é um parâmetro real diferente de zero e de 1), a velocidade do condutor relativamente a este referencial é agora igual a e a velocidade das linhas de campo magnético relativamente a este referencial é . Neste referencial existe campo magnético uniforme não-estático e também campo elétrico induzido dado por:
| (9.5) |
A força de Lorentz neste referencial tem pois componentes elétrica e magnética, e a soma delas é, como deve ser, igual à força de Lorentz nos outros dois referenciais:
| (9.6) |
O campo elétrico induzido num condutor produz corrente elétrica no sentido da sua componente tangencial ao condutor. É como se no condutor existisse uma f.e.m. induzida igual ao integral de linha do campo induzido ao longo do condutor:
| (9.7) |
ligada no sentido que produz corrente no sentido da componente tangente do campo induzido.
No caso da barra condutora da figura 9.2, o campo elétrico induzido aponta na direção da barra e o resultado do integral na equação (9.7) é:
| (9.8) |
em que é o comprimento da barra.
A grande diferença entre o campo elétrico induzido por campos magnéticos não-estáticos e o campo elétrico produzido por cargas (campo eletrostático), é que o primeiro não tem de ser conservativo como no caso do campo eletrostático. O integral (9.7) ao longo de um percurso fechado pode ser diferente de zero como veremos nas secções seguintes.
Exemplo 9.1
O dispositivo na figura seguinte é chamado gerador de Faraday. Um disco condutor, de raio , roda com velocidade angular dentro de um campo magnético uniforme e perpendicular ao disco.
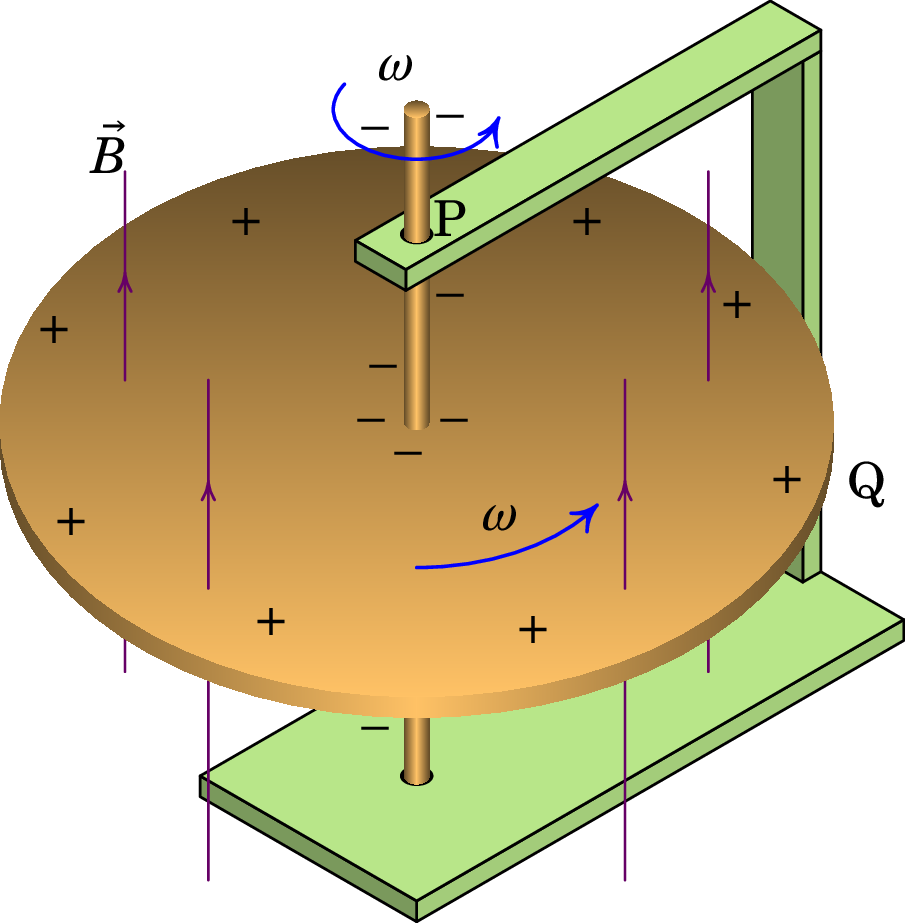
Determine a f.e.m. induzida entre o eixo do disco e um ponto na sua periferia.
Resolução. A velocidade dum ponto no disco, é tangencial, no plano do disco. O seu produto vetorial com o campo magnético é na direção radial e com módulo . Nos pontos que estão a uma distância do eixo, o módulo da velocidade é e o módulo do campo elétrico induzido é igual a:
| (9.9) |
A f.e.m. induzida entre o eixo do disco e um ponto na sua periferia é igual ao integral de linha do campo elétrico induzido entre esses pontos
| (9.10) |
9.2 Fluxo magnético
Define-se fluxo magnético através duma superfície S, igual ao integral de superfície do campo magnético:
| (9.11) |
A continuidade do campo magnético implica que o integral em (9.11) é igual a um valor médio da componente normal do campo na superfície, , vezes a área da superfície:
| (9.12) |
A f.e.m. induzida num condutor em movimento num campo magnético pode ser também obtida em função do fluxo magnético que atravessa o condutor, por unidade de tempo, como se mostra no seguinte exemplo.
Exemplo 9.2
Uma barra condutora, de comprimento , desliza sobre dois trilhos metálicos paralelos, com velocidade . Os extremos dos trilhos estão ligados a duas resistências e , como mostra a figura. Dentro do retângulo delimitado pelos trilhos e as resistências há campo magnético uniforme, perpendicular a ele e para dentro da figura. Determine a f.e.m. induzida na barra e mostre que é igual ao fluxo magnético que atravessa a barra, por unidade de tempo.
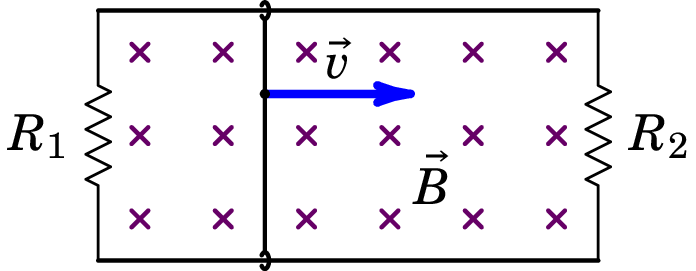
Resolução. O produto vetorial tem módulo igual a e aponta na direção tangente à barra. Como tal, usando a equação (9.8), a f.e.m. induzida na barra é igual a:
Num intervalo de tempo , as linhas de campo deslocam-se uma distância em relação à barra. O fluxo magnético que passa através da barra nesse intervalo é igual ao módulo do campo vezes a área, (o campo é normal a essa área):
e o fluxo por unidade de tempo é igual à f.e.m. induzida, .
9.2.1 Lei de Faraday
Em geral, quando o fluxo magnético através duma superfície varia em função do tempo, existe campo elétrico induzido. A lei de Faraday estabelece que:
Em qualquer curva fechada e orientada, se o fluxo magnético através da superfície delimitada pela curva varia, é induzida na curva uma força eletromotriz igual à menos a derivada do fluxo em ordem ao tempo.
Ou seja, a f.e.m. induzida ao longo de uma curva C orientada (ver figura 9.3) é dada pela expressão:
| (9.13) |
onde é o fluxo magnético através da superfície S delimitada por C, no sentido do versor normal , definido pela regra da mão direita seguindo a direção da curva C.
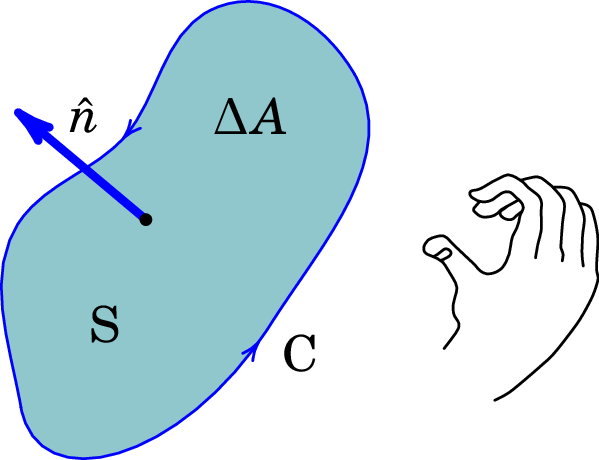
Como já foi referido, a f.e.m. induzida é também igual ao integral de linha do campo elétrico induzido, equação (9.7). Neste caso o percurso de integração é a curva fechada C e, como o integral de linha do campo eletrostático numa curva fechada é nulo, podemos escrever:
| (9.14) |
onde é o campo elétrico total, soma do campo eletrostático mais o campo elétrico induzido.
Na equação (9.13), o sinal de é o sinal do integral de linha do campo elétrico induzido ao longo da curva C. Se na curva C houver um fio condutor por onde pode circular corrente, a corrente induzida será no sentido de C se for positiva, ou no sentido oposto se for negativa.
Exemplo 9.3
A figura mostra um gerador de tensão alternada em que se faz rodar uma bobina dentro de um campo magnético uniforme; o fio onde começa a bobina está soldado a um anél condutor e o fim do fio, depois de ser enrolado na bobina, solda-se a outro anel condutor; enquanto a bobina roda, esses anéis mantêm-se em contato com duas escovas P e Q, que são os elétrodos do gerador.
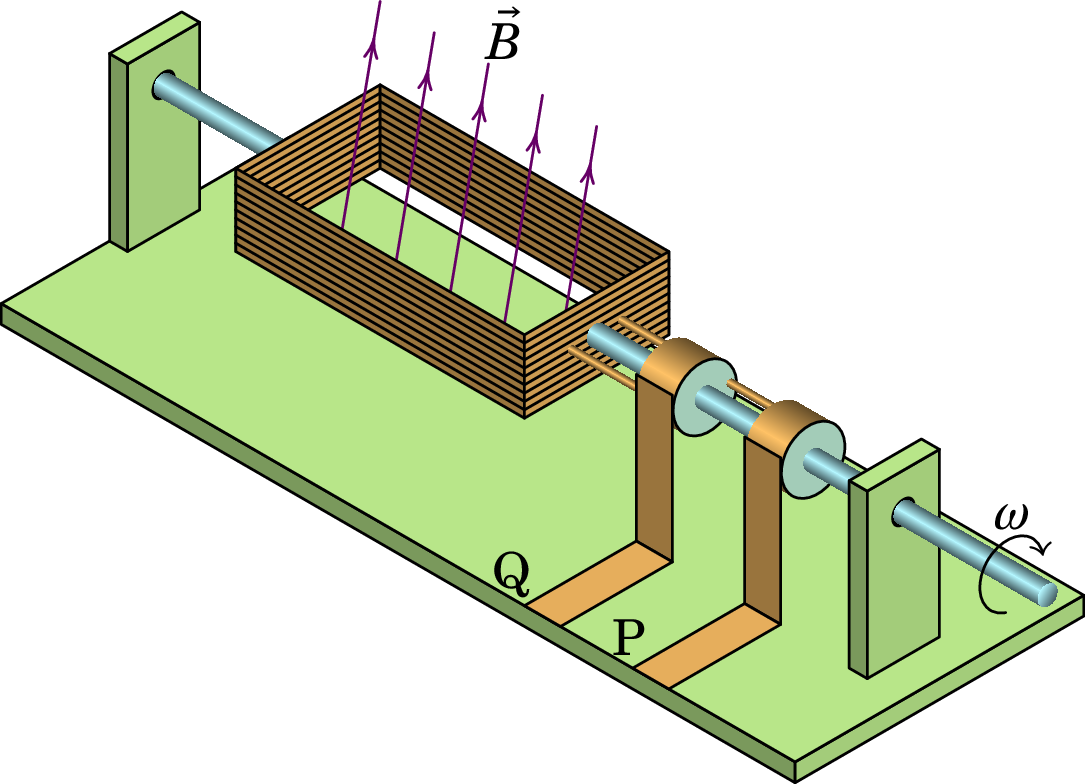
Resolução. O fluxo magnético através da bobina é:
onde é o número de espiras, o módulo do campo, a área de cada espira e o ângulo entre o campo e o versor normal à bobina.
A f.e.m. induzida entre os elétrodos do gerador é:
onde é a velocidade angular da bobina (derivada de em ordem ao tempo). Se for constante, o ângulo , em função do tempo, é dado por , e a f.e.m. induzida é uma função sinusoidal:
| (9.15) |
onde . Esse tipo de tensão denomina-se tensão alternada.
O gerador de tensão alternada, também chamado alternador, usa-se para gerar energia elétrica a partir de energia mecânica. A fonte da energia mecânica, que faz rodar a bobina, pode ser o vento, nas centrais de energia eólica, a corrente da água, nas centrais hidroelétricas, etc.
9.2.2 Lei de Lenz
O sinal da f.e.m. induzida pode também ser determinado pela lei de Lenz:
A força eletromotriz induzida é sempre no sentido que produz corrente induzida que contraria a variação do fluxo magnético.
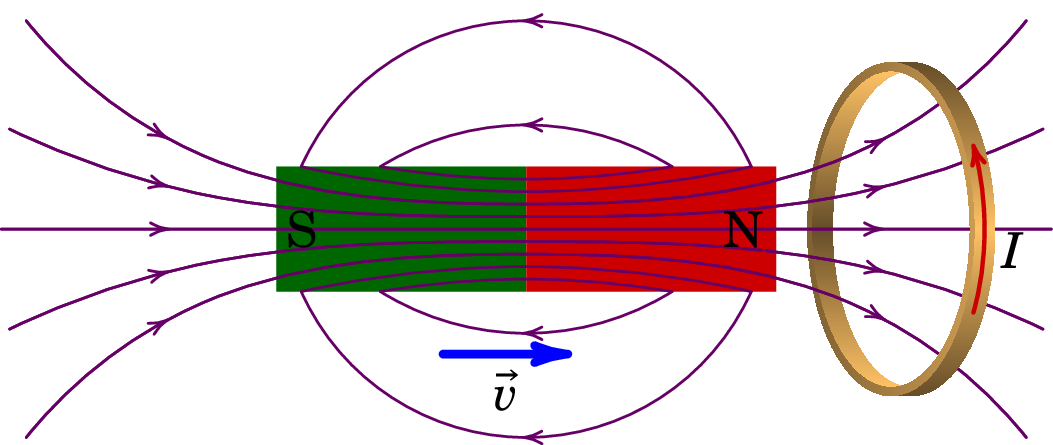
No exemplo apresentado na figura 9.4, em que um íman aproxima-se de uma espira condutora com velocidade (ver problema 9.9.9), o fluxo magnético no anel é no sentido da esquerda para a direita e está a aumentar. Aparece então corrente induzida no anel, dando origem a fluxo magnético da direita para a esquerda, que contraria o aumento do fluxo externo. A corrente é no sentido indicado na figura, que pela regra da mão direita produz campo magnético de direita para esquerda.
No exemplo 9.2, a f.e.m. induzida na barra produz corrente de baixo para cima. A figura 9.5 mostra o circuito equivalente ao dispositivo, com uma fonte ideal ligada a duas resistências em paralelo.
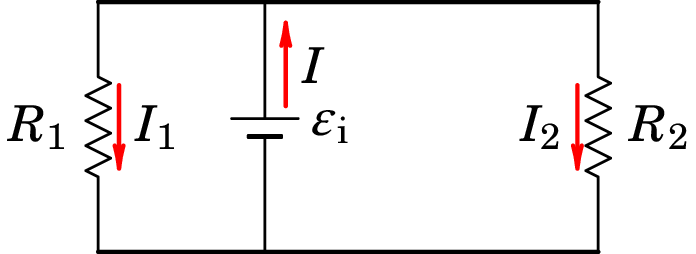
Na malha do lado esquerdo há fluxo magnético para dentro da folha, que está a aumentar. A corrente nessa malha produz campo magnético para fora da folha, que contraria o aumento desse fluxo. Na malha do lado direito o fluxo magnético é também para dentro da folha, mas está a diminuir. O sentido da corrente nessa malha implica campo magnético para dentro da folha, que reforça o fluxo magnético, contrariando a sua diminuição.
9.3 Auto-indução
A corrente numa bobina produz campo magnético que atravessa a área delimitada pela bobina, como mostra a figura 9.6. A bobina produz fluxo magnético através de si própria e qualquer alteração da corrente na bobina dá origem a variação desse fluxo, produzindo força eletromotriz induzida, a qual contraria a alteração da corrente.

O campo magnético produzido pela bobina é diretamente proporcional à corrente. Como tal, o fluxo magnético produzido pela bobina sobre si própria é proporcional à corrente:
| (9.16) |
e a constante chama-se indutância da bobina 11A indutância é também designada por coeficiente de auto-indução.. A f.e.m. auto-induzida na bobina é igual a menos a derivada do fluxo magnético através dela:
| (9.17) |
Quanto maior for a área das espiras na bobina, maior será a sua indutância. E quanto maior for o número de espiras, , na bobina, maior será também a área atravessada pelas linhas de campo e maior o módulo do campo magnético. A indutância de uma bobina com espiras é diretamente proporcional a (ver exemplo a seguir). A indutância da bobina é vezes a indutância de cada uma das suas espiras separadamente:
| (9.18) |
Todos os dispositivos têm indutância, mas geralmente o valor dessa indutância é muito baixo, podendo ser ignorado, exceto no caso das bobinas ou solenoides. Um dispositivo com indutância não-desprezável é chamado indutor. Usaremos algum dos diagramas de circuito na figura 9.7 para representar o indutor; no diagrama do lado esquerdo, o valor da f.e.m. auto-induzida é dada pela equação (9.17). No diagrama do lado direito, os sentidos da tensão e a corrente são definidos de forma consistente com o que temos feito em resistências e condensadores e a relação entre e é,
| (9.19) |
O sinal positivo, em contraste com o sinal negativo na equação (9.17), é porque no lado esquerdo a f.e.m. induzida é um elemento ativo, com sentido consistente com o sentido da corrente, enquanto que no lado direito o indutor é visto como elemento passivo, com os sinais de opostos aos sinais de .
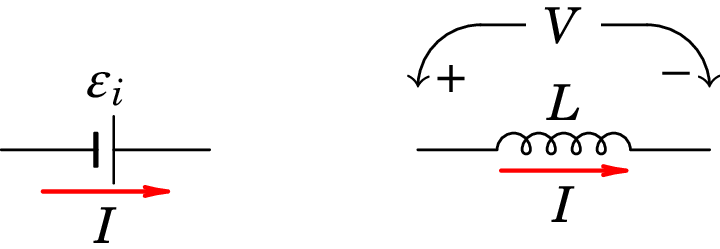
O diagrama de circuito de uma bobina ou solenoide é uma resistência em série com um indutor (figura 9.8), sendo a resistência elétrica da bobina ou solenoide. Admitindo positiva no sentido indicado na figura 9.8, a relação entre a diferença de potencial na bobina e a corrente através dela é a seguinte:
| (9.20) |
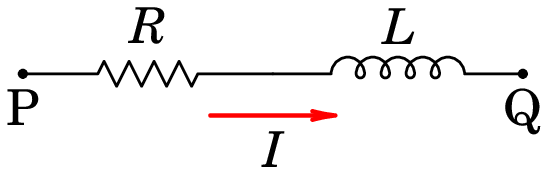
O primeiro termo na equação (9.20) é a lei de Ohm, consequência do efeito Joule na bobina (dissipação de energia elétrica em calor) e o segundo termo é a lei de Faraday, consequência da auto-indução na bobina.
No sistema internacional de unidades (SI), a unidade de indutância é o henry, representado pela letra H. A partir da equação (9.19) podemos concluir que:
| (9.21) |
Exemplo 9.4
Determine a indutância de um solenoide comprido, de comprimento , com espiras circulares de raio .
Resolução. O campo magnético dentro do solenoide é aproximadamente uniforme e com módulo (equação (8.13)):
Como o campo é perpendicular ao plano das espiras, o fluxo através de cada espira é igual à sua área vezes o módulo do campo; o fluxo através do solenoide é vezes o fluxo através de cada espira:
A indutância do solenoide é igual a:
9.3.1 Energia magnética e campo magnético
A potência associada a um indutor, usando a expressão (9.19), é dada por:
| (9.22) |
A energia magnética armazenada num indutor, caracterizado por uma indutância e percorrido por uma corrente eléctrica , é obtida integrando a potência em ordem ao tempo:
| (9.23) |
onde a constante de integração é nula, pois quando a corrente é nula a energia tem de ser nula. A indutância de um indutor dá-nos uma medida da capacidade deste armazenar energia magnética.
A energia magnética pode ser associada à energia armazenada no campo magnético. Como exemplo ilustrativo, consideremos um solenoide possuindo espiras circulares de raio de comprimento longitudinal no vácuo, o qual trataremos na aproximação de solenoide infinito. Usando as expressões (8.13), (8.9) e a expressão da indutância obtida no exemplo 9.4 na expressão (9.23) obtém-se que:
| (9.24) |
O valor corresponde ao volume interno do solenoide, onde existe campo magnético, pelo que o membro do lado direito da expressão acima corresponde à densidade volúmica de energia magnética, a qual num ponto de vetor posição é:
| (9.25) |
sendo J/m a sua unidade SI. A energia magnética total armazenada no campo magnético é obtida integrando a densidade volúmica de energia magnética em todo o espaço:
| (9.26) |
onde t.e. significa, “todo o espaço”.
9.4 Circuitos com indutores
Num circuito com fontes de tensão contínua, as correntes atingem o estado estacionário em que permanecem constantes. Nesse estado, a equação (9.19) implica tensão nula em todos os indutores, mas a corrente neles pode ter qualquer valor. Como tal, no estado estacionário os indutores são equivalentes curtos-circuitos (condutores com resistência nula).
Em qualquer instante em que se altera o estado estacionário, por ligar ou desligar alguma fonte, ou por abrir ou fechar algum interruptor, a corrente nos indutores não muda de forma instantânea porque, de acordo com a equação (9.19), a derivada da corrente deve existir em qualquer instante, i.e., é uma função contínua. Já nas resistências, condensadores e fontes de tensão pode ter descontinuidades nos instantes em que se altera o estado estacionário. Contudo, nestes instantes a voltagem nos indutores não tem de ser nula.
Conclui-se então que em qualquer instante em que é feita alguma mudança repentina no circuito, a voltagem num indutor pode ter qualquer valor, mas a corrente deverá ter o mesmo valor que tinha imediatamente antes da mudança ter acontecido. Se no instante em que se altera o estado estacionário do circuito a corrente no indutor é nula, o indutor é equivalente a um interruptor aberto, onde a corrente é nula, mas a sua voltagem pode ter um valor qualquer.
Após o instante em que há uma alteração repentina do circuito, as correntes nos indutores mudam gradualmente (resposta transitória). Mas como não podem mudar indefinidamente, o circuito atinge novamente o estado estacionário em que as correntes nos indutores se aproximam de valores constantes.
Exemplo 9.5
Uma bobina com 10 e 30 mH liga-se a duas resistências e a uma fonte de f.e.m. (ver figura). Determine a corrente na resistência de 2 k, no instante em que se fecha o interruptor e muito tempo após esse instante. Qual a relação entre essas duas correntes?
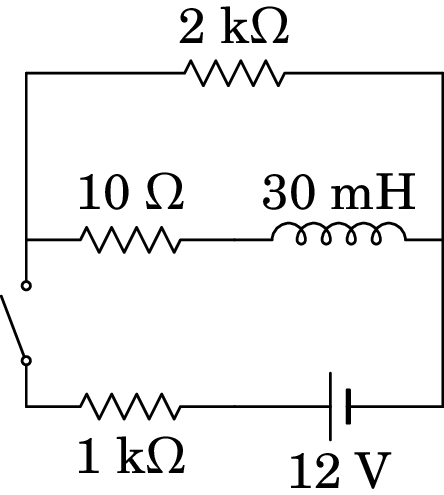
Resolução. Como antes de ser fechado o interruptor não passa corrente pelo indutor, no instante inicial o indutor é equivalente a um interruptor aberto, ou seja, não circula corrente pela resistência de 10 e é como se essa resistência e o indutor não existissem. Ignorando esses dois elementos, o circuito corresponde a uma única malha com a fonte e as duas resistências de 1 k e 2 k em série. Nesse instante, a corrente nessas duas resistências é:
Para calcular a corrente final, substitui-se o indutor por um curto-circuito:
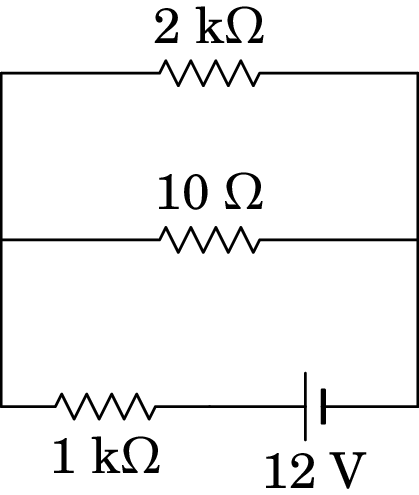
as resistências de 2 k e 10 estão em paralelo, podendo ser substituídas por uma única resistência com valor 200010 = 2/201 k, que fica em série com a resistência de 1 k e a resistência equivalente entre os terminais da fonte é
a corrente final que sai da fonte é mA e a diferença de potencial na resistência de 2 k é
a corrente final na resistência de 2 k é:
A razão entre as correntes inicial e final é:
O exemplo anterior mostra uma das propriedades importantes dos indutores que os torna muito úteis como balastros, dispositivos em que a corrente inicial é elevada mas a corrente final é muito menor. Os balastros são usados nas lâmpadas fluorescentes em que é necessária uma corrente elevada quando a lâmpada é ligada, para garantir a ionização do gás dentro do tubo tornando-se condutor; após a ionização do gás, se a corrente mantivesse o valor inicial elevado, a lâmpada queimar-se-ia.
9.4.1 Circuito RL
O circuito RL na figura 9.9 está inicialmente ligado a uma fonte de f.e.m. usada para fornecer corrente inicial no indutor. Num instante designado por abre-se o interruptor S para desligar a fonte do circuito RL e o diagrama do circuito passa a ser o que está representado no lado direito da figura.
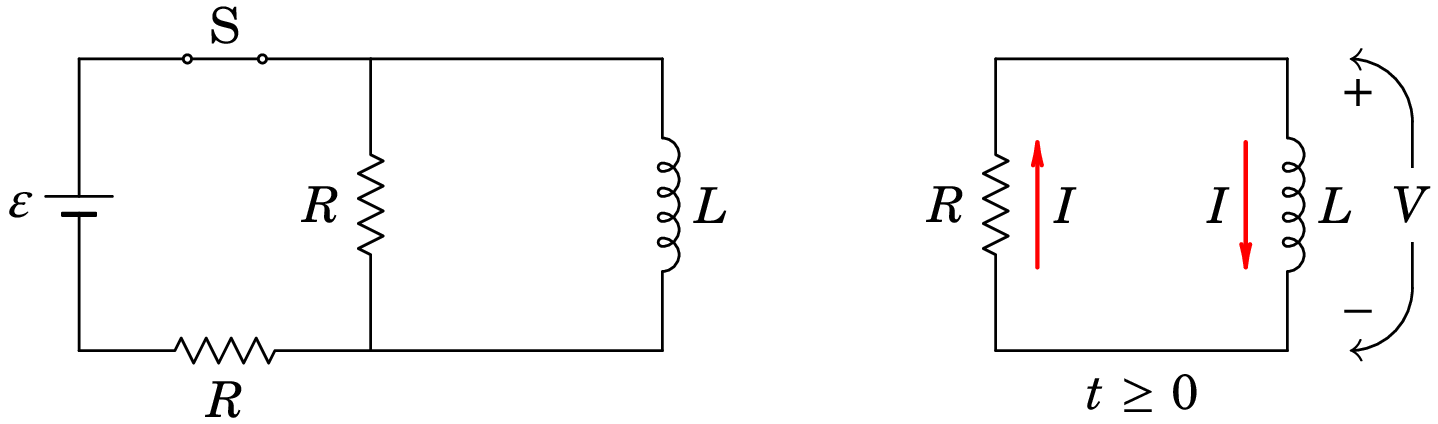
Se a fonte estiver ligada o tempo suficiente antes de o interruptor ser aberto, o indutor atinge o estado estacionário, em que a tensão nele é nula e a corrente igual a ; a corrente passa toda pela resistência de de baixo e na resistência do meio a corrente é nula. A resistência usa-se para evitar que a corrente se aproxime de infinito. No instante em que o interruptor acabou de se aberto, a corrente no indutor persiste, com valor inicial . Mas agora essa corrente circula pela resistência do meio.
Em , a tensão e a corrente , nos sentidos definidos na figura 9.9 estão relacionados pela equação (9.19):
| (9.27) |
Na resistência, a corrente e a tensão são as mesmas do que no indutor, mas o sentido positivo da corrente é oposto ao sentido positivo da tensão (corrente a passar de menor para maior potencial) e a lei de Ohm na resistência é,
| (9.28) |
Como no instante inicial a corrente é igual a , a equação anterior mostra que a tensão inicial é (se as duas resistências usadas não fossem iguais este valor inicial seria diferente, mas ainda negativo). A tensão no indutor muda abruptamente de 0 para em . O sinal negativo indica que o indutor atua como elemento ativo e não passivo, como foi admitido na figura 9.9.
Equação esta com a mesma forma da equação (6.30) do circuito RC analisado na secção 6.6.1 e, como vimos, a solução desta equação é a tensão inicial vezes a função exponencial de :
| (9.30) |
A constante chama-se constante de tempo do circuito, porque tem unidades de tempo. Em unidades SI, um henry dividido por um ohm é igual a um segundo:
| (9.31) |
A figura 9.10 mostra o gráfico da tensão no indutor, expressão (9.30), em função do tempo. A reta a tracejado é a tangente à curva em . O seu declive é pois igual à derivada da função em . Usando a expressão (9.29), esse declive é igual a (a tensão inicial é ) e a equação da reta é então:
| (9.32) |
a qual corta o eixo do tempo em .
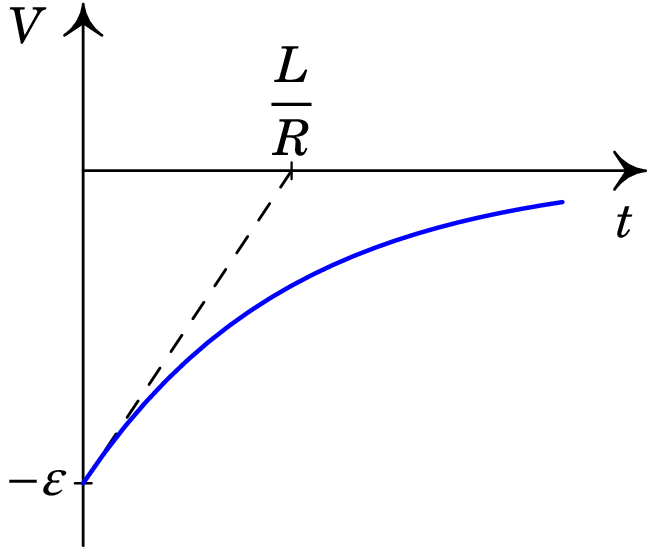
A tensão aumenta exponencialmente, desde até zero. Se continuasse a aumentar à mesma taxa inicial (i.e., linearmente), demorava um tempo igual à constante de tempo para ficar igual a zero. Quanto maior for a constante de tempo, mais lento será o aumento exponencial da tensão.
A corrente calcula-se a partir da tensão usando a equação (9.28)
| (9.33) |
que é uma função exponencial que diminui desde a corrente inicial até zero.
9.5 Forma integral e diferencial da lei de Faraday
Seja C uma curva fechada e orientada que delimita uma superfície S. Como a curva C é fixa, na derivada do fluxo magnético através de S (equação (9.11)) basta derivar o campo, já que S e permanecem constantes:
| (9.34) |
observe-se que a derivada temporal tornou-se derivada parcial, porque depende da posição e do tempo. Combinando as equações (9.13), (9.14) e (9.34) a lei de Faraday pode ser escrita da forma seguinte:
| (9.35) |
Que é uma relação fundamental entre os campos elétrico e magnético, válida em qualquer curva fechada e orientada, C, e respetiva superfície S delimitada por C.
Usando o teorema de Stokes (A.81) no integral do lado esquerdo, obtém-se
| (9.36) |
e no limite em que a área de S aproxima-se de zero, ficando apenas um ponto, nesse ponto verifica-se:
| (9.37) |
Se o campo magnético depende do tempo, o rotacional do campo elétrico é diferente de zero e, como tal, não é um campo conservativo. Quando o campo magnético é estático, não há campo elétrico induzido e o rotacional de é nulo; o campo elétrostático nesse caso é conservativo e é devido às cargas livres.
9.6 Corrente de deslocamento
Maxwell percebeu que a lei de Ampère (8.8) só podia ser válida no caso em que o campo elétrico é estático. Se assim não for, deve-se acrescentar à corrente através da curva C outra corrente , denominada por corrente de deslocamento. A equação obtida é desginada de lei de Ampère-Maxwell:
| (9.38) |
A lei de Ampère é válida unicamente nos casos em que o campo elétrico é estático ou nulo, fazendo com que a corrente de deslocamento seja nula. O integral de linha do campo , numa curva fechada C, pode ser diferente de zero inclusivamente quando não passa corrente através da curva, devido à corrente de deslocamento. Corrente essa que deverá depender da derivada temporal do fluxo elétrico através do interior da curva C, tal como na lei de Faraday (9.35) a derivada temporal do fluxo magnético produz integral de linha do campo ao longo de uma curva fechada C.
Para determinar a expressão da corrente de deslocamento em função do fluxo elétrico, consideremos o exemplo de um fio retilíneo sobre o semieixo negativo , que se estende desde até a origem (figura 9.11).
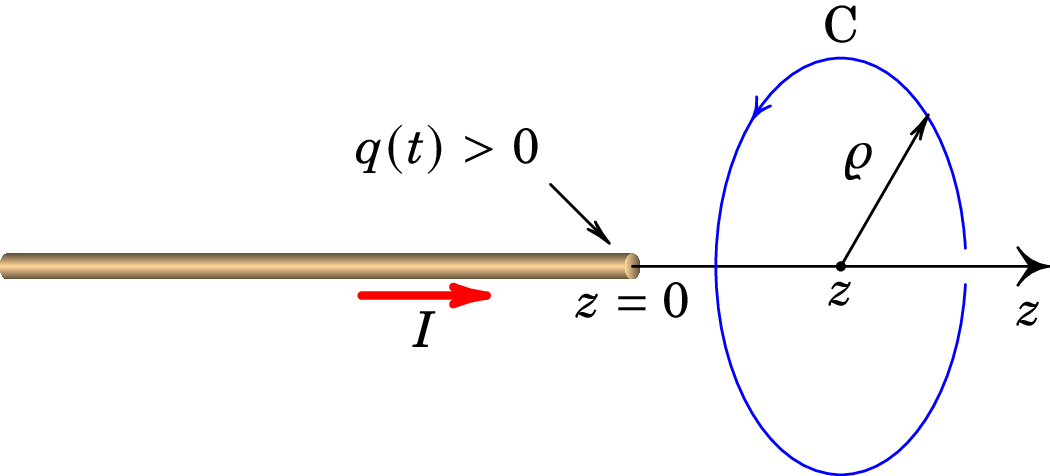
Se durante alguns instantes há corrente no fio, no sentido positivo do eixo , haverá acumulação de cargas positivas na origem. A carga acumulada na origem, é uma função do tempo, e a intensidade da corrente no fio é igual à derivada dessa função em ordem ao tempo:
| (9.39) |
Como existe simetria cilíndrica, as linhas do campo magnético produzido pela corrente no fio são circunferências perpendiculares ao eixo , com centro nele, orientadas no sentido da regra da mão direita segundo a direção positiva do eixo . Seja C uma circunferência perpendicular ao eixo , de raio e com centro no ponto de coordenada no eixo (ver figura 9.11). A curva C coincide com uma curva de campo , e escolhendo o sentido de C no sentido do campo, o integral de linha de ao longo de C é igual a ; usando a lei de Ampère-Maxwell (9.38), obtém-se o módulo do campo nos pontos com coordenada e a uma distância do eixo do fio:
| (9.40) |
O gráfico 9.12 mostra o módulo do campo magnético esperado, a uma distância fixa do eixo e variando a coordenada (centro das circunferências C). Longe da origem, com , a corrente de deslocamento é nula (a acumulação de cargas na origem não interessa). No limite a corrente através da curva é e a equação (9.40) conduz a . No limite a corrente através da curva é nula e o campo também é nulo.
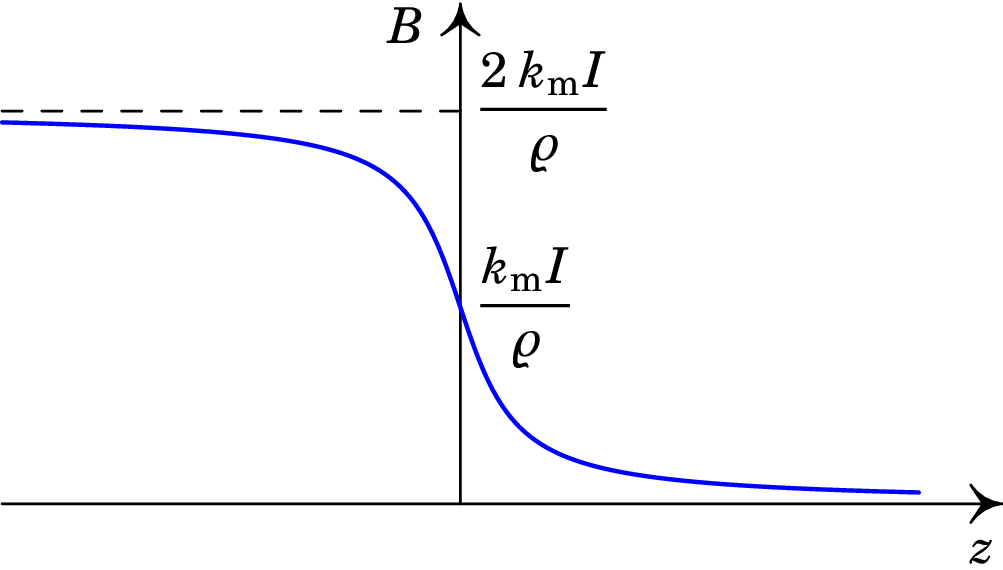
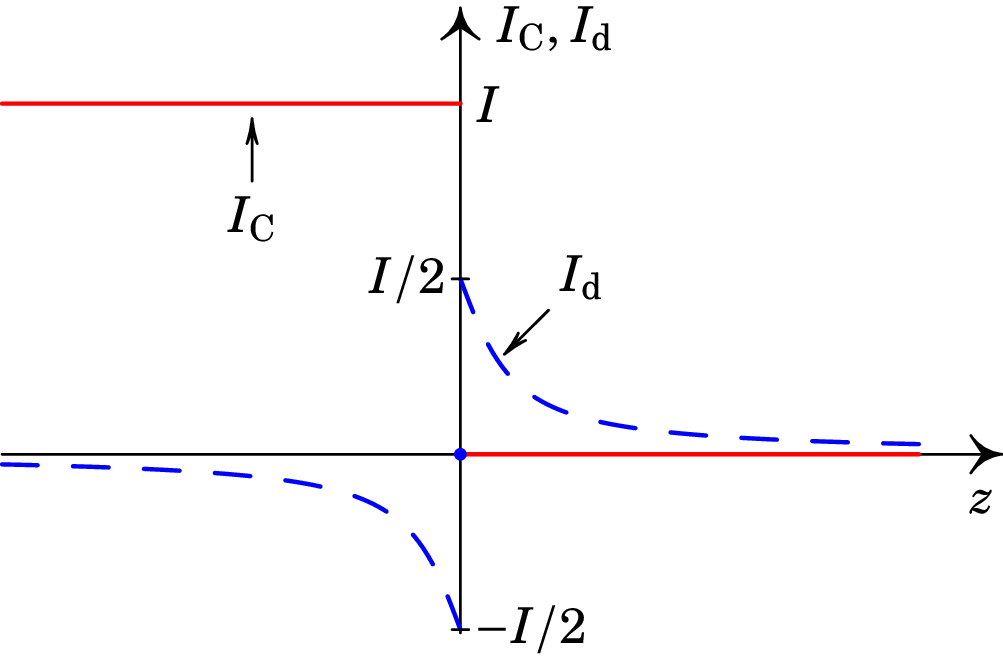
Em espera-se que tenha o valor intermédio e próximo da origem a corrente de deslocamento será importante para produzir o resultado da figura 9.12. O gráfico da figura 9.13 mostra a corrente através da circunferência C, em função da posição do seu centro (linha contínua a vermelho), e a corrente de deslocamento (linha azul a tracejado) necessária para produzir o resultado da figura 9.12.
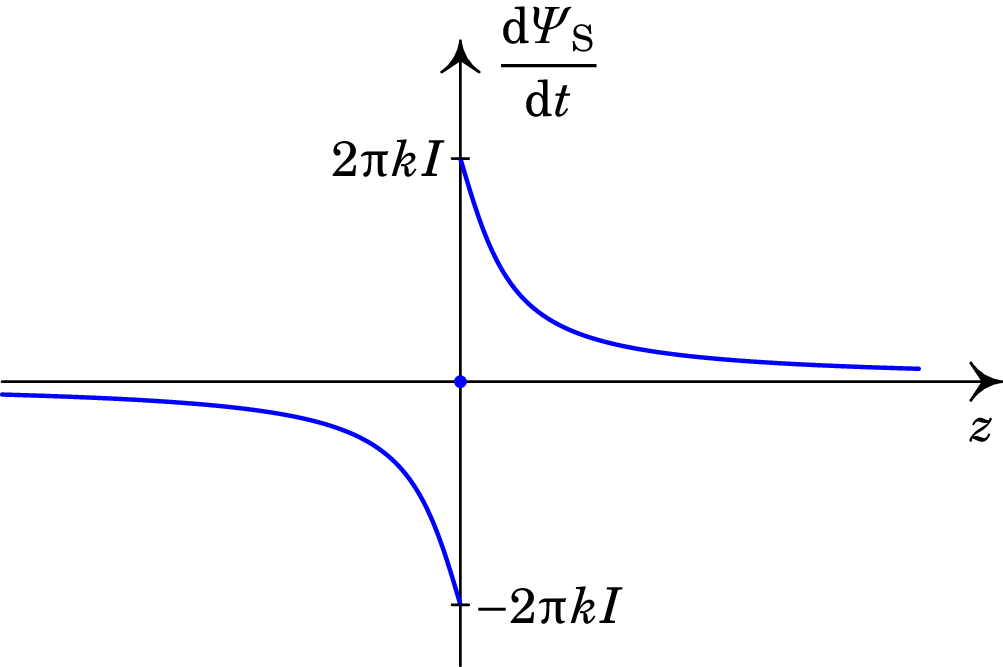
A carga produz campo elétrico e, portanto, fluxo elétrico através da superfície S delimitada pela circunferência C. O fluxo é negativo se o centro da circunferência estiver em , positivo se o centro estiver em ou nulo se o centro estiver em . Quando aproxima-se de zero, o fluxo através da circunferência aproxima-se de metade do fluxo total . Em o fluxo aproxima-se de na origem, e em aproxima-se de na origem. Tendo em conta a relação (9.39) entre a carga e a corrente no fio, o gráfico da derivada do fluxo elétrico é como mostra a figura 9.14, passando de para na origem.
Comparando o gráfico da figura 9.14 com a curva a tracejado na figura 9.13, conclui-se que a corrente de deslocamento deverá ser dada pela seguinte expressão:
| (9.41) |
Exemplo 9.6
Um fio retilíneo de comprimento é percorrido por corrente de intensidade . Usando a lei de Ampère-Maxwell, determine o módulo do campo magnético produzido a uma distância do fio e mostre que o resultado é o mesmo que foi obtido no exemplo 8.1, usando a lei de Biot-Savart.
Resolução. Os pontos à mesma distância do fio e equidistantes de um dos extremos são equivalentes e, portanto, as linhas de campo são circunferências C perpendiculares ao fio, com centro nele, e no sentido da regra da mão direita segundo a direção da corrente, tal como mostra a figura seguinte.
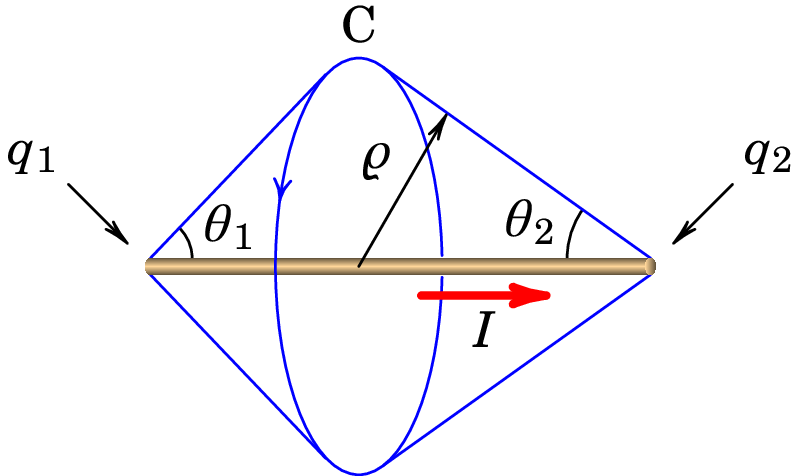
Aplicando a lei de Ampère-Maxwell, obtém-se mesma expressão (9.40) para o módulo do campo. A corrente no fio finito implica acumulação de cargas, e , nos dois extremos, com derivadas:
Cargas essas que produzem fluxo elétrico variável e corrente de deslocamento através do interior da circunferência C:
onde e são os fluxos elétricos produzidos por e . Cada um desses fluxos é igual ao fluxo através da calota esférica que C delimita na esfera com centro em ( igual a 1 ou 2), e raio . Nessas esferas o campo elétrico é perpendicular e com valor ; o fluxo é igual a esse valor do campo vezes área da calota, que pode ser calculada integrando o elemento diferencial de área da esfera,em coordenadas esféricas (equação (A.60)), com ângulo zenital entre 0 e (ver figura acima):
e multiplicando pelos valores dos campos elétricos, os fluxos elétricos são:
A derivada temporal de é a mesma expressão de , substituindo por . Na figura acima observa-se que a variação de ambos fluxos é no sentido negativo da curva C e, como tal, a corrente de deslocamento é igual a:
A corrente através de C é igual a (se o centro de C estiver sobre o fio, como na figura acima). A corrente total é,
e substituindo na equação (9.40) obtém-se o mesmo resultado do exemplo 8.1:
No caso em que o centro da circunferência C estiver fora do fio, será nula, o fluxo produzido pela carga mais próxima de C, por exemplo , mudará de sinal e a calota esférica com centro em terá ângulo . Assim, a corrente total nesse caso será,
e a expressão para é a mesma obtida quando o centro de C está sobre o fio.
Observe-se que a corrente de deslocamento garante a continuidade da corrente total através da circunferência C, quando o seu centro passa de do fio para fora dele.
Problemas
-
9.1.
O comprimento total entre as pontas das asas de um avião Boeing 747 é 60 m . O avião voa a 800 km/h e com altura constante, na direção sul-norte, numa região onde o campo magnético terrestre faz um ângulo de 60 com a vertical e a sua intensidade é 0.5 G. Calcule a diferença de potencial induzida entre as pontas da asas.
-
9.2.
A figura mostra uma barra condutora de comprimento e massa que desliza sobre dois trilhos metálicos verticais, dentro de um campo magnético uniforme. A resistência elétrica dos trilhos e da barra são desprezáveis comparadas com . A barra mantém sempre o contato com os trilhos, permitindo que circule corrente pela resistência , mas o atrito é desprezável, assim como o efeito da resistência do ar na barra. Quando a barra começa a cair livremente, o seu movimento é inicialmente acelerado mas rapidamente atinge uma velocidade constante . Calcule o valor dessa velocidade limite .
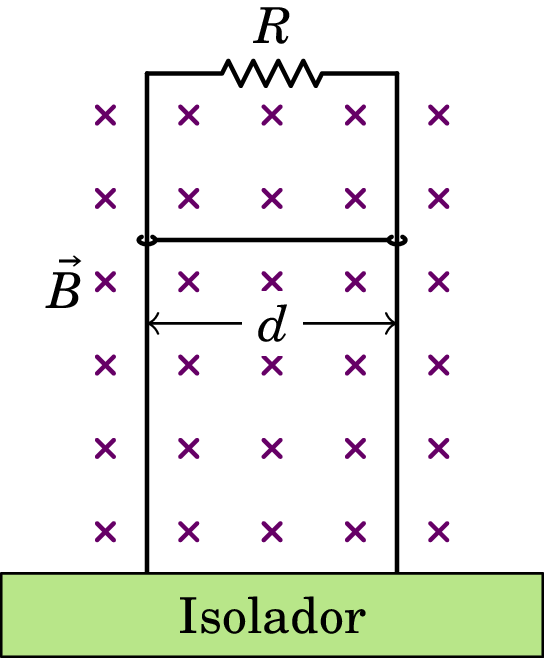
-
9.3.
Uma bobina retangular com 400 espiras, todas com arestas de 1.5 cm e 3 cm, é atravessada por um campo magnético externo de módulo 0.2 T, perpendicular aos planos das espiras. A resistência total da bobina é 42 . Ligam-se entre si os dois extremos, inicial e final, da bobina e o campo externo é reduzido até 0, durante um intervalo de 4 segundos. Determine a carga total transferida através da bobina durante esse intervalo.
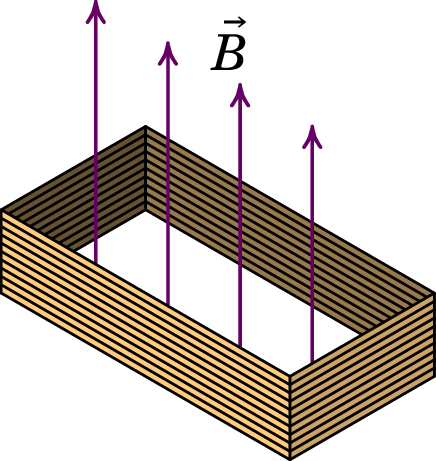
-
9.4.
A bobina cilíndrica na figura tem 23 espiras de raio 1.6 cm. O eixo da bobina coincide com o eixo dos , em , mas em roda no plano com velocidade angular constante , no sentido indicado na figura. Na região onde a bobina roda existe campo magnético variável:
Determine a expressão da f.e.m. induzida na bobina, em função do tempo , para .

-
9.5.
A espira retangular na figura tem arestas cm e cm. No mesmo plano da espira encontra-se um fio condutor retilíneo e muito comprido, paralelo a uma das arestas de lado e a uma distância cm dela. Determine a expressão da f.e.m. induzida na espira, em função do tempo , quando o fio retilíneo é percorrido por corrente com intensidade (unidades SI).
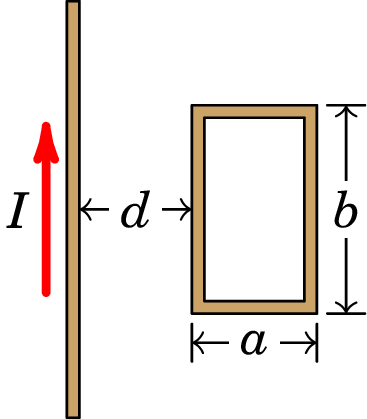
-
9.6.
Uma espira condutora retangular, paralela ao plano O, desloca-se com velocidade constante (m/s) dentro de uma região onde existe um campo magnético com componentes: (SI) e . Calcule a f.e.m. induzida na espira, em função do tempo , a partir do instante em que a espira se encontra na posição da figura, com um lado ao longo do eixo dos .
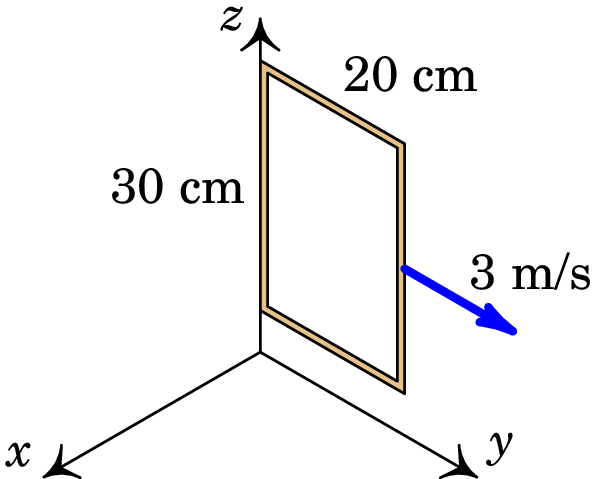
-
9.7.
No circuito da figura, calcule as correntes iniciais no indutor e no condensador, a corrente final no indutor e a carga final no condensador.
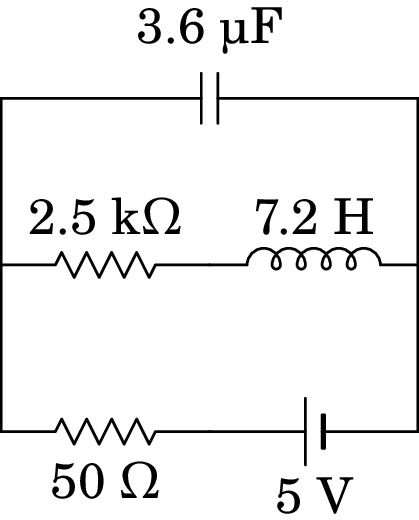
-
9.8.
No circuito representado no diagrama, a fonte foi ligada no instante , quando não havia corrente no indutor.
(a) Determine a voltagem na resistência de 3.4 k em .
(b) Determine o valor da derivada da voltagem na resistência de 3.4 k, em .
(c) Determine a voltagem na resistência de 3.4 k, quando o circuito atingir o estado estacionário.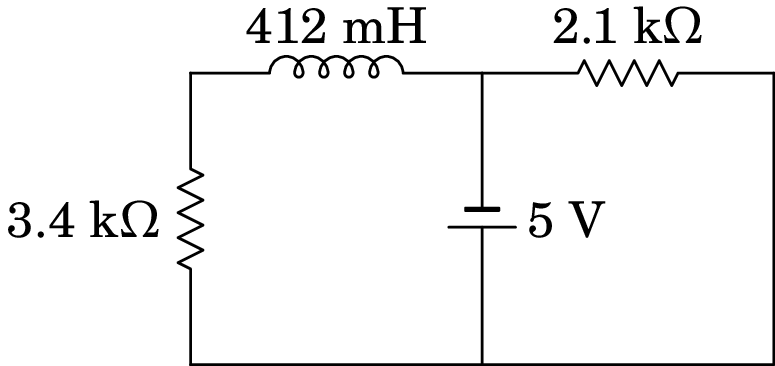
-
9.9.
Um íman desloca-se ao longo do eixo de uma espira, aproximando-se dela, com velocidade constante, como mostra a figura. Usando o sentido positivo da espira como definido na figura:
(a) Represente num gráfico, de forma qualitativa, o fluxo magnético através da espira em função do tempo . Indique o instante em que o íman está a meio da travessia da espira.
(b) Represente o gráfico da corrente na espira em função do tempo.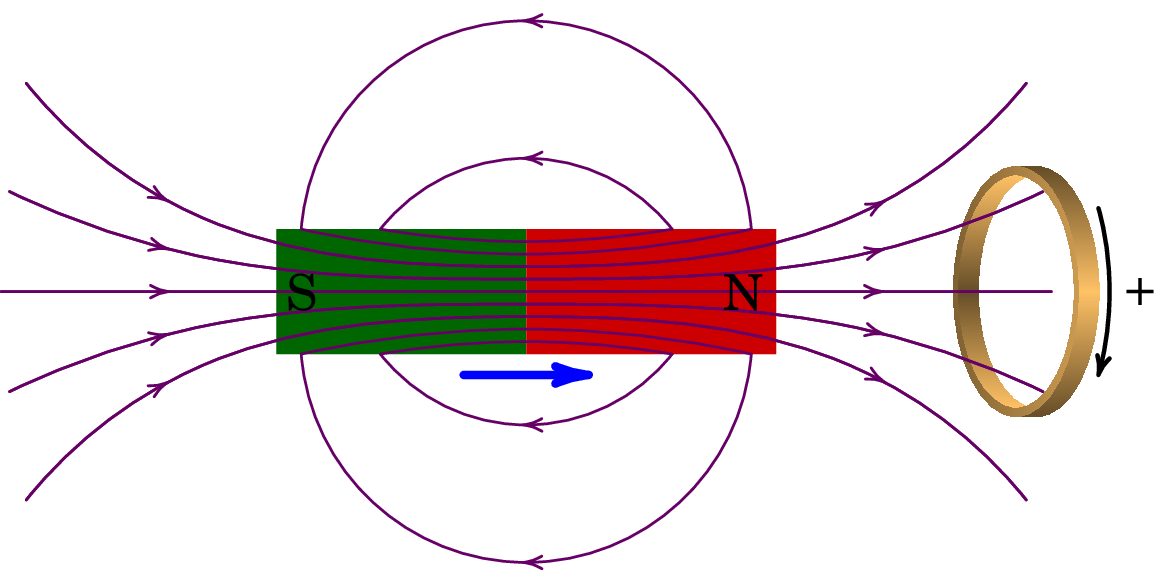
-
9.10.
Uma barra metálica de comprimento cm desloca-se com velocidade constante cm/s, numa região onde há campo magnético uniforme com intensidade G, perpendicular à barra (ver figura). Determine o valor da f.e.m. induzida na barra.

-
9.11.
O plano de uma espira quadrada de cobre, com 4 cm de lado, está na posição horizontal. Coloca-se um eletro-íman em forma de barra na posição vertical, acima do plano da bobina e com o seu polo norte mais próximo da espira mas um pouco afastado do seu centro, de tal forma que as linhas de campo magnético atravessam a espira formando um ângulo de 30 com a vertical. Calcule a f.e.m. induzida média na espira, enquanto a intensidade do campo magnético do eletro-íman, na superfície da espira, varia desde zero até um valor final de 0.5 T, num intervalo de 200 ms. Qual o sentido da corrente induzida na espira?
-
9.12.
(a) Mostre que, se o fluxo magnético através da cada espira de uma bobina de espiras e resistência variar de até , a carga total que passa através da bobina é dada por
(b) Uma bobina circular de diâmetro 2 cm, resistência de 50 e tem o seu eixo paralelo a um campo magnético uniforme e de módulo 1 T. Calcule a carga total que passa pela bobina quando a direção do campo é invertida.
(c) Se a inversão do campo na alínea anterior levar 0.1 s, calcule a corrente e a f.e.m. médias na bobina. -
9.13.
No interior da circunferência a tracejado na figura existe um campo magnético que aponta para lá da folha e com módulo que depende do tempo segundo a expressão (unidades SI). Determine a intensidade, direção e sentido do campo elétrico induzido dentro do anel condutor de raio cm.
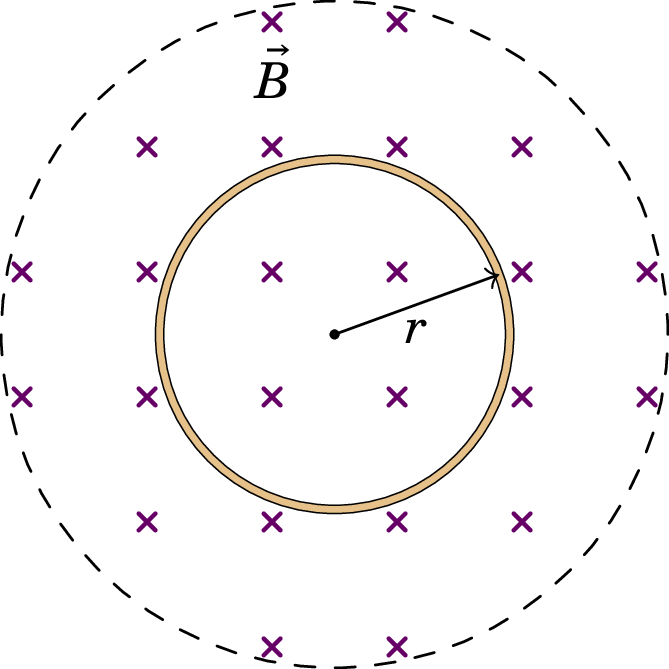
-
9.14.
Uma bobina cilíndrica (ou solenoide) de comprimento cm possui espiras circulares de raio cm. Como , podemos considerar a bobina como infinita.
(a) Calcule a indutância da bobina quando esta é percorrida por uma corrente elétrica constante de valores A, mA e mA.
(b) Determine a energia magnética armazenada na bobina para os três valores de corrente indicados na alínea anterior. -
9.15.
(a) No circuito da figura, o interruptor tem estado fechado durante muito tempo e o interruptor aberto; determine a corrente no indutor. (b) A seguir, abre-se o interruptor e simultaneamente fecha-se o interruptor ; nesse preciso instante, a corrente no indutor deve ter o mesmo valor calculado na alínea anterior. Explique qualitativamente o que acontece com a corrente no indutor e a carga no condensador a partir desse instante.
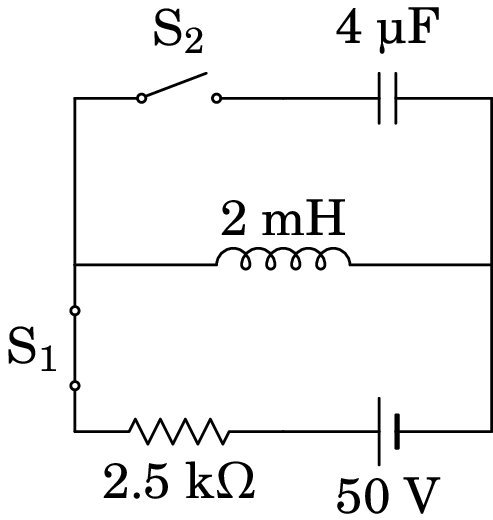
-
9.16.
No circuito representado no diagrama, a fonte foi ligada no instante , quando o condensador estava descarregado e não havia corrente no indutor. Determine as correntes em cada resistência em e quando o circuito atingir o estado estacionário.
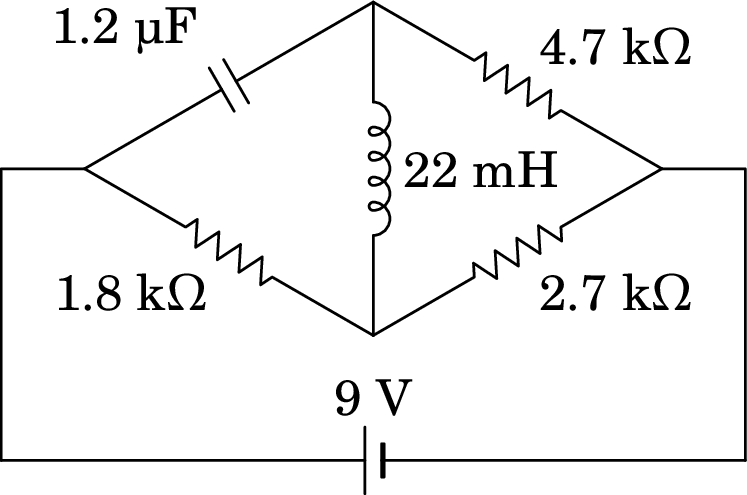
-
9.17.
A fonte no circuito do diagrama foi ligada no instante , quando a corrente nos dois indutores era nula.
(a) Determine a diferença de potencial em cada um dos dois indutores, no instante .
(b) Encontre o valor da derivada da corrente em cada indutor, em .
(c) Determine a intensidade da corrente em cada indutor, após o circuito atingir o estado estacionário.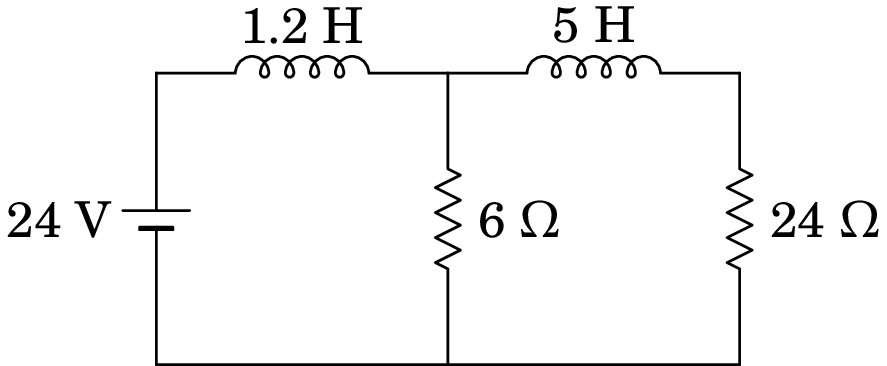
-
9.18.
Considere um condensador de armaduras circulares de raio , paralelas e planas, separadas por de ar. Num determinado instante, a corrente no condensador é 5 A.
(a) Calcule a derivada do campo elétrico entre as placas, em ordem ao tempo, nesse instante.
(b) Mostre que a corrente de deslocamento entre as placas é igual à corrente de 5 A.
(c) Porque razão as duas correntes são iguais?
Respostas
-
9.1.
0.33 V.
-
9.2.
.
-
9.3.
0.857 mC.
-
9.4.
-
9.5.
-
9.6.
V, no sentido anti-horário visto desde a esquerda.
-
9.7.
Inicialmente, 100 mA no condensador e 0 no indutor. No fim, 1.96 mA no indutor e 17.6 µC no condensador.
-
9.8.
(a) 0. (b) 41.26 kV/s. (c) 5 V.
-
9.9.
Contando o número de linhas de campo que atravessam a espira em instantes sucessivos , , , …, observa-se que o fluxo (sempre positivo) aumenta até um valor máximo, em e logo diminui:
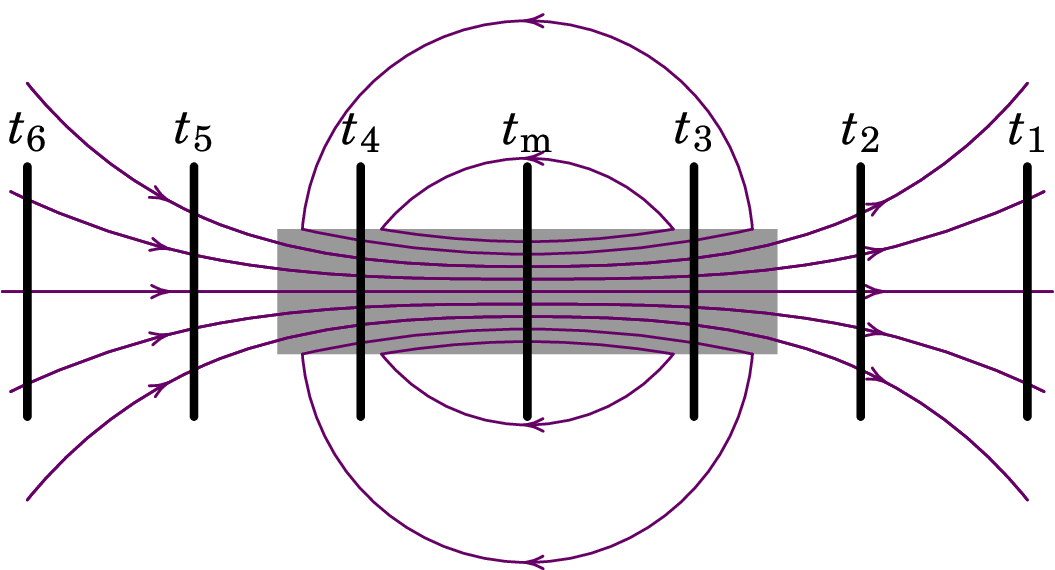
A corrente é proporcional à derivada do fluxo, com sinal negativo.
(a)
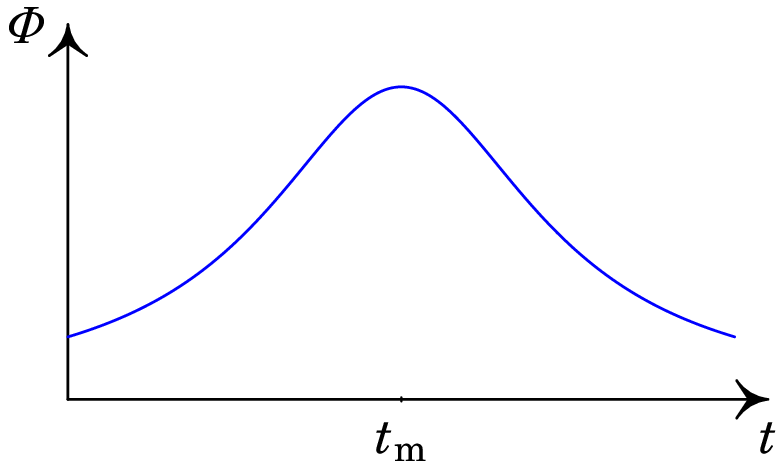
(b)
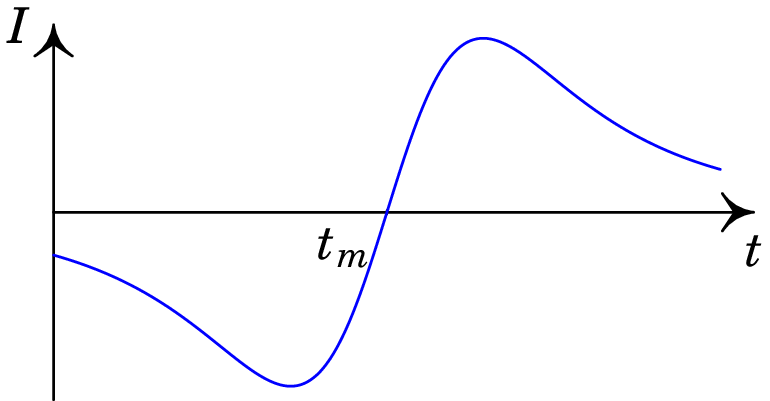
-
9.10.
V.
-
9.11.
3.5 mV. Vista de cima, a corrente na espira tem sentido anti-horário.
-
9.12.
(b) 1.26 mC. (c) 12.6 mA e 0.628 V.
-
9.13.
, na direção tangente ao anel e no sentido horário.
-
9.14.
(a) H. (b) J, nJ e nJ.
-
9.15.
(a) 20 mA. (b) A corrente diminui enquanto a carga aumenta; quando a corrente decresce até zero, a carga atinge um valor máximo e nesse momento, o condensador começa a descarregar, surgindo uma corrente que aumenta, no sentido contrário à corrente inicial. Quando a carga diminui até zero, a corrente é máxima e com a mesma intensidade inicial. O ciclo repete-se indefinidamente, pois não existe nenhuma resistência que dissipe energia.
-
9.16.
Em , 1.91 mA na resistência de 4.7 k, e 2.0 mA nas resistências de 1.8 k e 2.7 k. No estado estacionário, 2.56 mA na resistência de 1.8 k, 0.93 mA na resistência de 4.7 k, e 1.63 mA na resistência de 2.7 k.
-
9.17.
(a) 24 V no indutor de 1.2 H, e 0 no indutor de 5 H. (b) 20 A/s no indutor de 1.2 H, e 0 no indutor de 5 H. (c) 5 A no indutor de 1.2 H, e 1 A no indutor de 5 H.
-
9.18.
(a) V/(m·s). (b) e substituindo a expressão de da alínea anterior conclui-se que . (c) Considerando uma curva fechada C que envolve o condensador, paralela às armaduras, para que o integral de linha de ao longo dessa curva seja contínuo fora das armaduras e entre elas, a som deve ser constante e, como fora das armaduras e , entre as armaduras e deverá ser igual a .