8. Cálculo do campo magnético

André Marie Ampère (1775–1836)
O estudo da eletricidade avançou a grandes passos nas primeiras décadas do século XIX, após a invenção da pilha de Volta. No entanto, a relação entre os fenômenos elétricos e magnéticos era desconhecida, apesar de que já tinha sido observado que quando uma casa é atingida por um raio, alguns objetos metálicos ficavamm magnetizados —por exemplo os talheres. Em 1820 Hans Christian Ørsted (1777–1851) revolucionou o estudo da eletricidade e do magnetismo ao descobrir que um fio atravessado por corrente elétrica produz campo magnético à sua volta; poucos dias após o anúncio dessa descoberta Jean-Baptiste Biot e Felix Savart, encontraram uma expressão matemática para o campo magnético em função da corrente. De forma independente, Ampère estudou a relação entre a corrente e o campo magnético descobrindo que existem forças magnéticas entre dois fios atravessados por corrente.
8.1 Campo magnético de fios com corrente
Em 1820, Hans Christian Ørsted realizou uma experiência na qual observou que um fio percorrido por uma corrente elétrica fazia mover uma bússola, tal como um íman natural o faria. A conclusão desta experiência é que um condutor percorrido por uma corrente elétrica estacionária (constante) produz um campo magnético estático (não dependente do tempo).
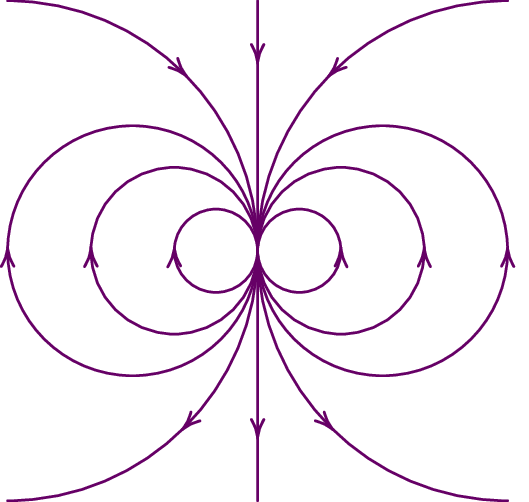
As linhas do campo magnético produzido por um fio retilíneo com corrente são circunferências perpendiculares ao fio e com centro no eixo do fio, como se mostra na figura 8.1. O sentido do campo segue a regra da mão direita, em relação à corrente: colocando o polegar da mão direita no sentido da corrente, os outros dedos indicam o sentido das linhas de campo magnético.
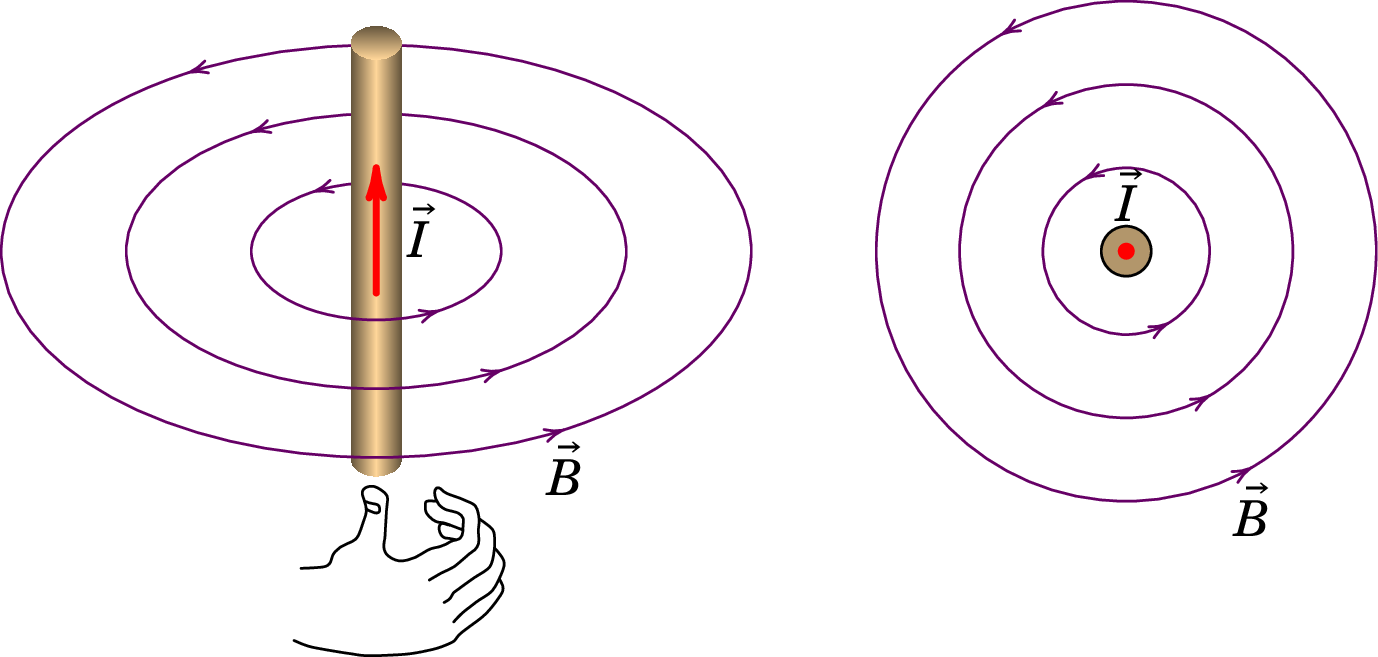
O Princípio da Sobreposição também se aplica ao campo magnético: o campo magnético devido a um sistema é igual à soma vetorial dos campos individuais de cada elemento do sistema. A soma dos campos de vários fios retilíneos e paralelos são curvas planas, no plano perpendicular aos fios.
As linhas de campo magnético de um sistema de fios retilíneos com corrente são idênticas às curvas equipotenciais de um sistema de fios retilíneos e paralelos, com densidade linear de carga constante, no plano perpendicular aos fios. As correntes em sentidos opostos assemelham-se a fios com densidade de carga de sinais opostos. No entanto, as linhas de campo magnético são verdadeiras curvas, orientadas num sentido, enquanto que as curvas equipotenciais são realmente a interseção de superfícies com um plano e não têm um sentido definido.
A figura 8.2 mostra dois exemplos. No corte com o plano perpendicular, os fios aparecem como pequenos círculos; as correntes para dentro da figura representam-se com um X e as correntes para fora da figura com um ponto. No lado esquerdo estão representadas as linhas de campo magnético de dois fios com correntes da mesma intensidade e sentido. Há um ponto de campo nulo no meio do segmento entre os fios. Na figura do lado direito, em que as correntes são em sentidos opostos, o ponto de campo nulo está fora do segmento entre as cargas. Nos pontos mais afastados dos fios, as linhas de campo aproximam-se de circunferências, com centro num ponto entre os dois fios, percorridas no sentido da mão direita segundo o sentido da soma das correntes nos dois fios.
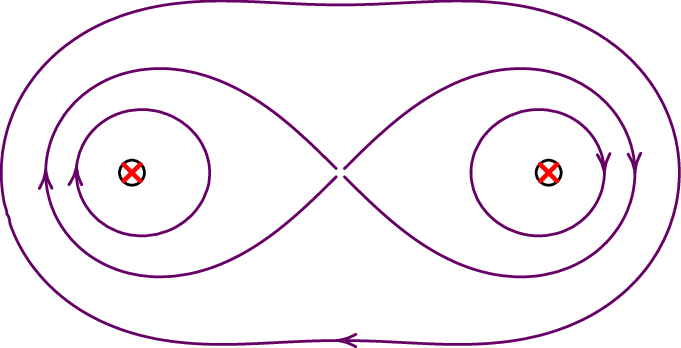
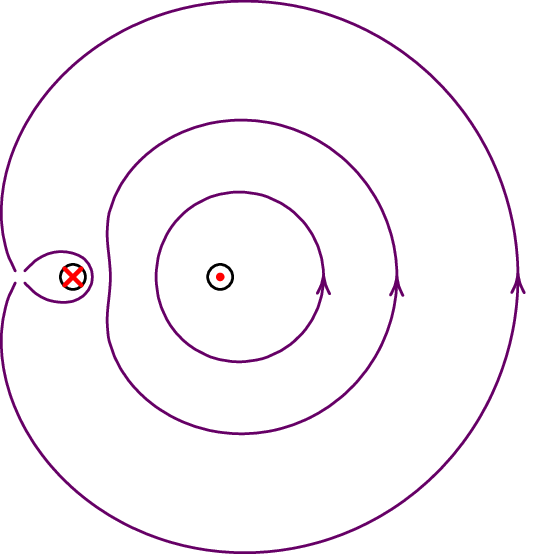
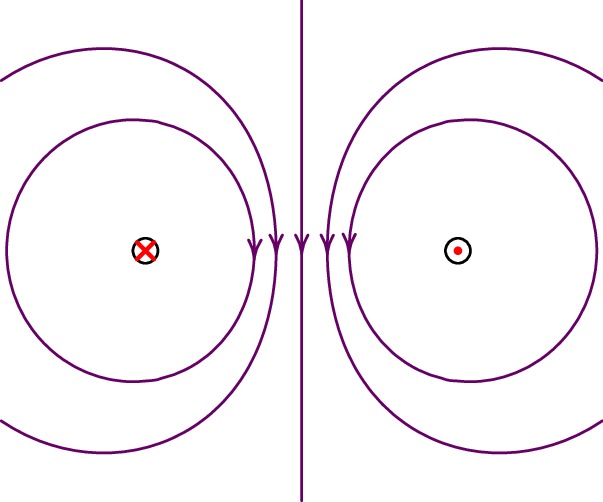
Num sistema de dois fios paralelos com corrente, o ponto de campo nulo encontra-se sempre mais próximo da corrente mais fraca, no segmento entre os dois fios se o sentido das correntes é o mesmo, ou fora desse segmento se os sentidos das correntes é oposto. O único caso em que não existe ponto de campo nulo, e as linhas de campo nos pontos afastados não são circunferências com centro entre os dois fios, é quando as correntes têm a mesma intensidade, com sentidos opostos. A figura 8.3 mostra as linhas de campo nesse caso, no lado esquerdo na região próxima dos fios e no lado direito nos pontos muito afastados, onde os dos fios parecem passar pelo mesmo ponto.
 |
 |
8.2 Lei de Biot-Savart
A lei de Biot-Savart estabelece a expressão do campo magnético devido a uma corrente estacionária percorrendo um segmento de fio entre dois pontos P e Q. O campo magnético num ponto de vetor posição é dado pelo seguinte integral de linha ao longo do fio:
| (8.1) |
onde é o vetor posição dos pontos do fio entre P e Q, é o elemento infinitesimal de comprimento ao longo do fio, o vetor vai desde cada ponto do fio até ao ponto onde se calcula o campo e o vetor corrente possui módulo igual à corrente elétrica e a direção e o sentido da corrente elétrica (ver figura 8.4).
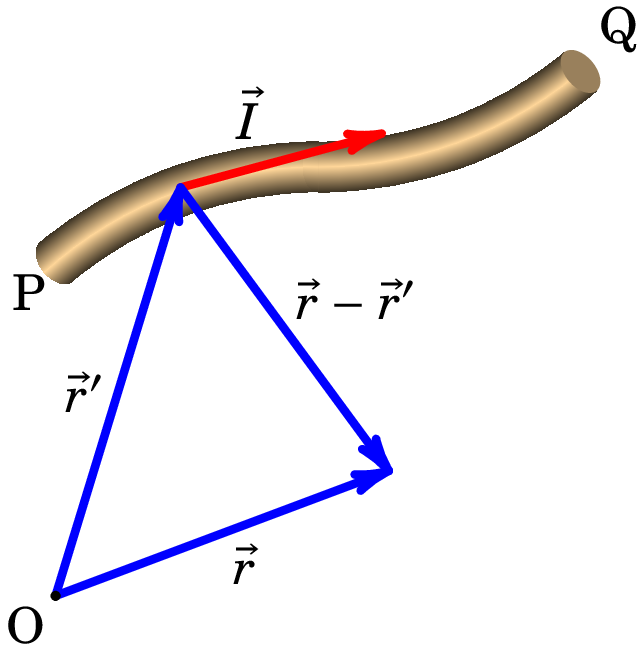
Observe-se que o vetor corrente pode mudar de direção mas tem módulo constante ao longo do integral. A constante magnetostática tem o seguinte valor experimental, no Sistema Internacional de unidades,
| (8.2) |
A equação (8.1) é semelhante à equação (2.8) do campo elétrico produzido por um fio com densidade linear de carga . No entanto, o produto vetorial com a corrente faz com que o campo magnético produzido por cada elemento infinitesimal de fio não seja um campo central e, como tal, não seja conservativo como no caso do campo elétrico. A seguir veremos alguns exemplos de aplicação da lei de Biot-Savart.
Exemplo 8.1
Calcule o campo magnético produzido por um fio retilíneo, finito, com corrente .
Resolução. Podemos escolher o eixo ao longo do fio, no sentido da corrente, e a origem no ponto que faz com que o vetor posição , do ponto P onde vamos calcular o campo, esteja no plano , tal como mostra o lado esquerdo da figura seguinte.
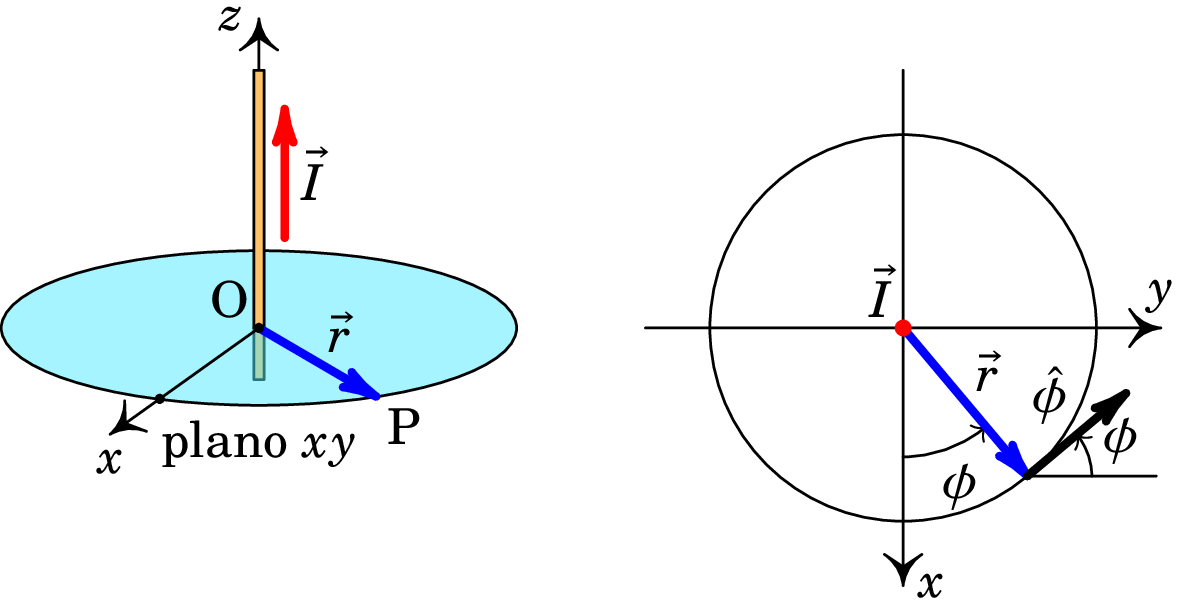
Usando coordenadas cilíndricas (secção A.2.3 do apêndice A), os vetores posição , (um ponto no fio) e são os seguintes (ver lado direito da figura acima):
Como tal,
onde é o versor azimutal no ponto P (ver figura acima). E o módulo de é igual a . Substituindo na lei de Biot-Savart (8.1),
O integral pode ser resolvido com a substituição trigonométrica
que conduz ao resultado:
Para escrever o resultado sem referência a nenhuma origem O, a figura seguinte mostra o fio, entre os pontos e , os ângulos e e dois ângulos e definidos em relação ao fio e ao ponto P onde se calcula o campo:
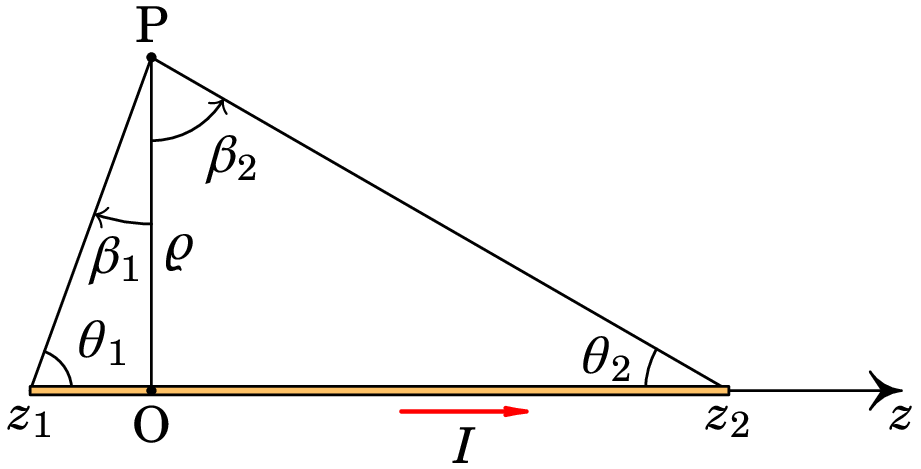
Como e o campo magnético em qualquer ponto é:
em que é a distância desde o ponto até à reta que passa pelo fio e o versor azimutal em relação ao eixo ao longo do fio e no sentido da corrente.
Num fio retilíneo infinito, os ângulos e aproximam-se de zero e . A expressão do campo do fio retilíneo infinito é então dada por:
| (8.3) |
onde é a distância desde o ponto até a reta que passa pelo fio e o versor azimutal em relação ao eixo ao longo do fio e no sentido da corrente.
8.3 Lei de Ampère
Consideremos um fio retilíneo infinito com corrente . As linhas de campo magnético são circunferências perpendiculares, com centro nele. Ao longo duma dessas circunferências C, de raio , o módulo do campo magnético é constante, igual a (equação (8.3)). Como tal, o integral de linha do campo magnético ao longo da circunferência C é,
| (8.4) |
resultado este que não depende do tamanho da circunferência, porque o comprimento da circunferência aumenta proporcionalmente a e o campo diminui proporcionalmente a .
De facto, o integral dá o mesmo resultado independentemente do tamanho e da forma da curva de integração. Isto pode mostrar-se usando coordenadas cilíndricas, com eixo dos ao longo do fio no sentido da corrente. O campo magnético do fio é dado pela equação (8.3) e o deslocamento vetorial infinitesimal é dado pela equação (A.49) do apêndice A:
| (8.5) |
O integral de linha do campo magnético em qualquer curva fechada C é então,
| (8.6) |
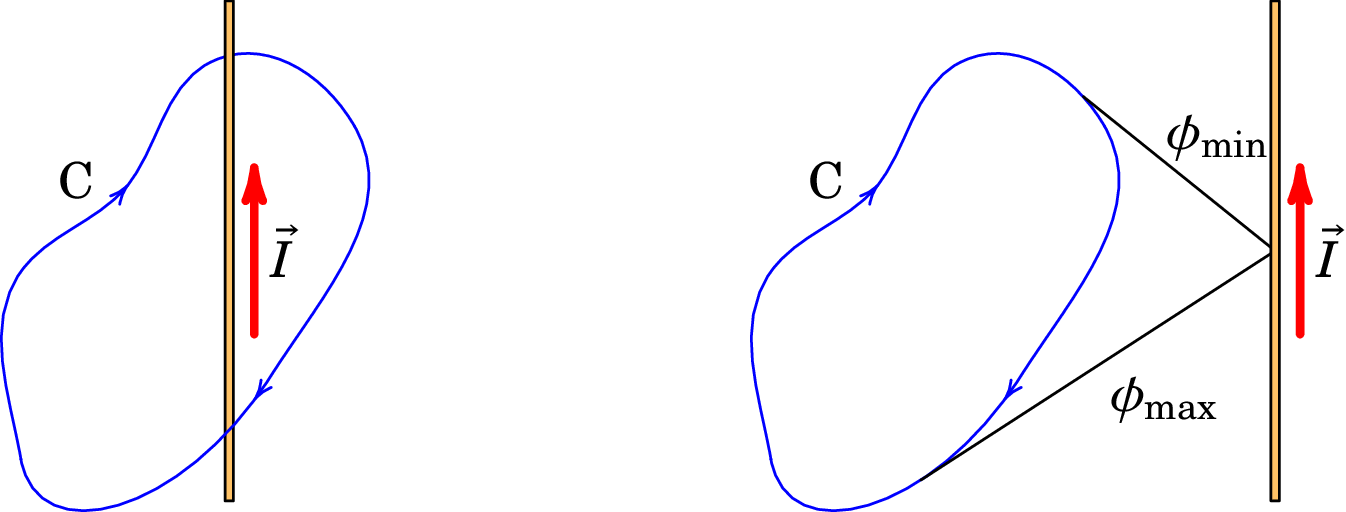
Se o fio atravessa o interior da curva C, como no lado esquerdo da figura 8.5, na curva C o ângulo varia entre 0 e . No entanto, observe-se que na figura 8.5 o sentido da corrente indica que aumenta no sentido contrário aos ponteiros do relógio, enquanto que a curva C é percorrida no sentido oposto; isso implica que o integral na equação (8.6) é igual a . Já se a curva tivesse sido percorrida no mesmo sentido em que aumenta (sentido da regra da mão direita em relação à corrente no fio), o resultado seria .
Quando o fio não atravessa o interior da curva C, como no lado direito da figura 8.5, o integral na equação (8.6) varia desde um ângulo mínimo até um ângulo máximo . A curva C pode ser dividida em duas partes: uma parte que vai desde até , onde o integral é igual a , e uma segunda parte em que vai desde até , onde o integral é igual a . Assim, o integral na curva completa é igual a zero.
Concluindo, o integral de linha do campo produzido por um fio retilíneo infinito, em qualquer curva fechada C, é:
| (8.7) |
No resultado anterior, a curva C não tem de ser plana nem perpendicular ao fio, tem sim de ser sempre fechada. A curva até pode dar várias voltas antes de fechar e, nesse caso o resultado da equação (8.7) deverá ser multiplicado pelo número de voltas .
Quando existem vários fios com correntes, o integral do campo é a soma dos integrais dos campos de cada fio. Nos fios que não atravessam o interior da curva C o integral é nulo e nos fios com corrente que atravessam o interior da curva o integral é . Somando os integrais obtém-se a lei de Ampère:
| (8.8) |
O integral de linha do campo magnético em qualquer curva fechada é igual à soma algébrica das correntes elétricas que atravessam o interior da curva vezes .
O lado direito na lei de Ampère também costuma ser escrito , onde é denominada permeabilidade magnética do vácuo e é igual a
| (8.9) |
Como veremos no capítulo 11, a lei de Ampère (8.8) é válida unicamente quando o campo elétrico é nulo ou estático. Quando existem campos elétricos variáveis no tempo, deverá ser acrescentado outro termo devido à denominada corrente de deslocamento. Pelo seu lado, a lei de Biot-Savart (8.1) é sempre válida.
No cálculo do campo magnético a lei de Ampère tem um papel semelhante ao da lei de Gauss no cálculo do campo elétrico. Em alguns casos em que existe alguma simetria das linhas de campo magnético consegue-se calcular o campo a partir da lei de Ampère, como veremos no exemplo seguinte.
Exemplo 8.2
Determine o campo magnético produzido por um fio cilíndrico infinito de raio , com corrente distribuída uniformemente na secção transversal do fio.
Resolução. Por simetria, o campo magnético deve ser tangente às circunferências C concêntricas e perpendiculares ao fio, conforme a figura abaixo.
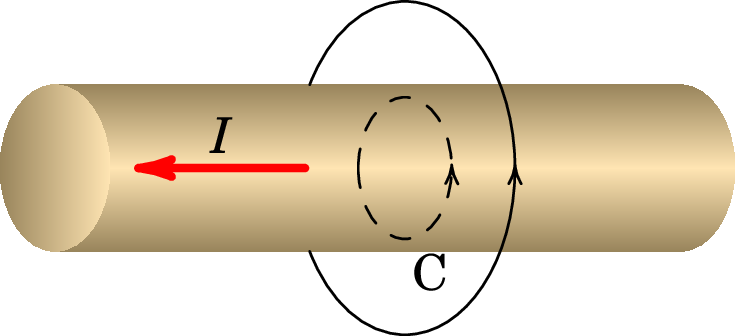
O integral de linha do campo magnético ao longo dessas circunferências, de raio , é igual a:
E usando a lei de Ampère, esse integral deverá ser também igual a:
Comparando as duas equações anteriores obtém-se a expressão do módulo do campo magnético:
Se o raio da circunferência C for maior do que o raio do fio cilíndrico, a corrente através de C será exatamente igual a . Já no caso de uma circunferência com raio , a corrente interna é igual ao produto da densidade de corrente vezes a área do círculo delimitado por C, . Como tal, a corrente que passa através de C é igual a:
E a expressão do campo magnético é,
onde é a distância desde o ponto até o eixo do fio cilíndrico e o versor azimutal em relação a esse eixo, no sentido da corrente.
A figura 8.6 mostra o gráfico do módulo do campo magnético, em função da distância ao eixo do fio cilíndrico. No interior do fio cilíndrico, o campo aumenta linearmente em função de , até um valor máximo ; fora do fio cilíndrico, o campo diminui inversamente proporcional a e o campo é igual ao campo magnético de um fio retilíneo ideal (raio nulo e comprimento infinito), o qual como vimos é dado pela expressão (8.3).
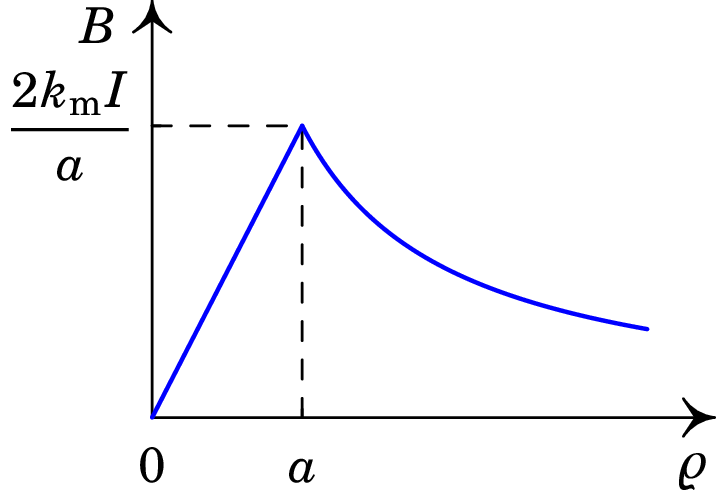
Como na prática não existem fios cilíndricos infinitos, o campo representado na figura 8.6 é uma boa aproximação para um fio cilíndrico de raio , quando o seu comprimento é muito maior do que e para pontos do espaço perto do seu centro.
8.4 Bobinas e solenoides
A figura 8.7 mostra o as linhas de campo magnético de uma espira ou bobina circular. Ao longo do eixo da bobina o campo magnético aponta na direção do momento magnético da bobina, i.e., na direção da normal no sentido da regra da mão direita de acordo com o sentido da corrente.
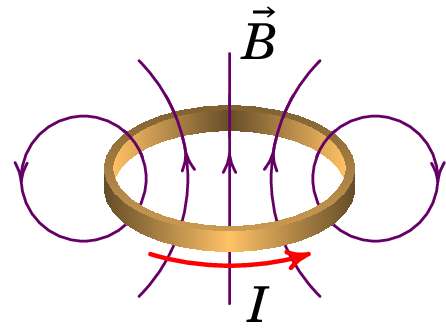
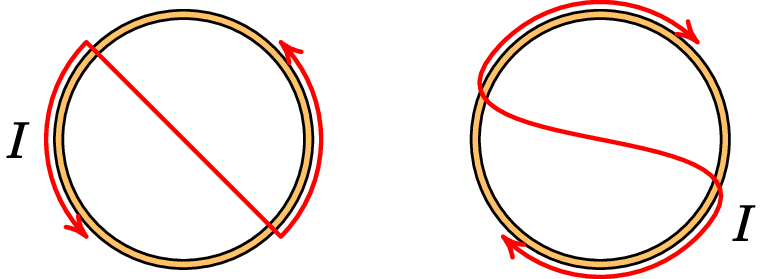
A bobina com corrente é equivalente a um íman em que o momento magnético da bobina aponta do polo sul para o polo norte. O extremo da bobina onde olhando para ela a corrente circula no sentido anti-horário (lado esquerdo da figura 8.8) é o polo norte e o extremo onde a corrente é vista no sentido horário (lado direito da figura 8.8) é o polo sul. A figura 8.8 mostra uma regra simples para identificar os polos magnéticos da bobina: os sentidos da corrente sugerem as letra N ou S, que indicam o polo norte ou sul.
Exemplo 8.3
Determine o campo magnético de uma espira circular de raio , com corrente , ao longo do eixo da espira.
Resolução. Seja o eixo no eixo da espira e no sentido positivo da regra da mão direita segundo o sentido da corrente, com origem no centro da espira.
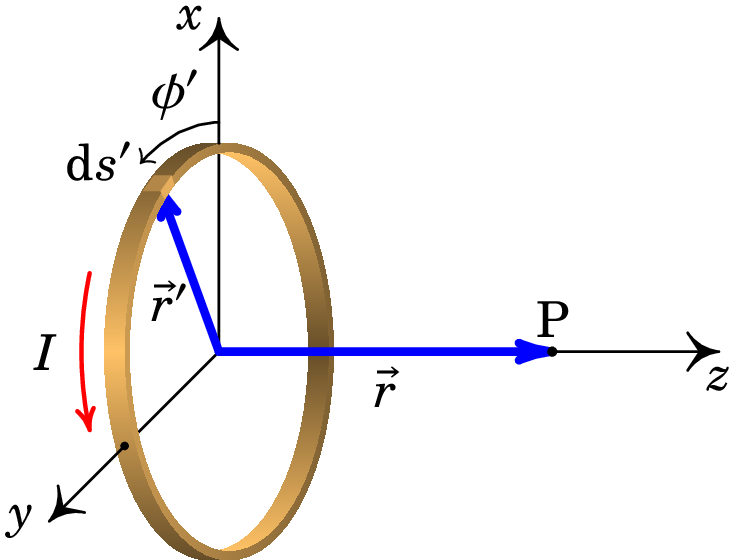
O vetor posição dum ponto P no eixo da espira é e o vetor posição dos pontos na espira, em função do ângulo azimutal , é igual a:
A corrente na espira, perpendicular a , é definida pelo vetor:
e o elemento diferencial de arco ao longo da espira é .
O produto vetorial entre e o vetor desde um ponto da espira até P é:
Substituindo na expressão (8.1) da lei de Biot-Savart,
Observe-se que é o momento magnético da espira. Como tal, o resultado pode também ser escrito como:
A figura 8.9 mostra o gráfico do módulo do campo magnético ao longo do eixo de uma espira de raio , obtido no exemplo anterior.
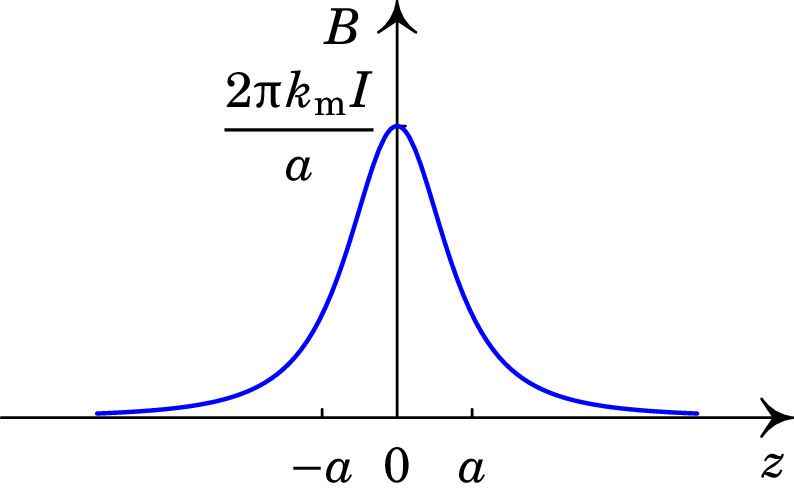
Note-se que o campo magnético é relativamente mais intenso no interior da espira do que no seu exterior, o que está de acordo com densidade de linhas de campo da figura 8.7. Do ponto de vista intituivo podemos pensar do seguinte modo. As linhas de campo magnético de um fio retilíneo com corrente possuem a mesma densidade à volta do fio (ver figura 8.1). Se agora encurvarmos o fio de modo a fazer uma espira, as linhas de campo possuirão maior densidade no interior desta. No caso de uma bobina circular, de raio e com espiras, o campo ao magnético é igual a vezes o campo de uma espira.
Um solenoide é uma bobina cilíndrica com comprimento maior do que o diâmetro, . Admitiremos que as espiras estão muito próximas e uniformemente espaçadas, de forma que o número de espiras por unidade de comprimento é constante e igual a . A corrente no solenoide circula realmente por uma curva helicoidal, mas se o número de voltas é elevado e estão muito próximas entre si, podemos aproximar essa hélice por uma sucessão de espiras circulares, todas com o mesmo raio e a mesma corrente . O campo magnético em qualquer ponto será a sobreposição dos campos produzidos por todas as espiras nesse ponto.
Exemplo 8.4
Determine o campo magnético produzido por um solenoide de raio e espiras por unidade de comprimento, ao longo do seu eixo, em função da intensidade da corrente .
Resolução. Escolhemos o eixo ao longo do eixo da bobina, no sentido da regra da mão direita segundo o sentido em que roda a corrente, e a origem no ponto P onde vamos determinar o campo, tal como na figura seguinte, que mostra o corte do solenoide com um plano que passa pelo seu eixo:
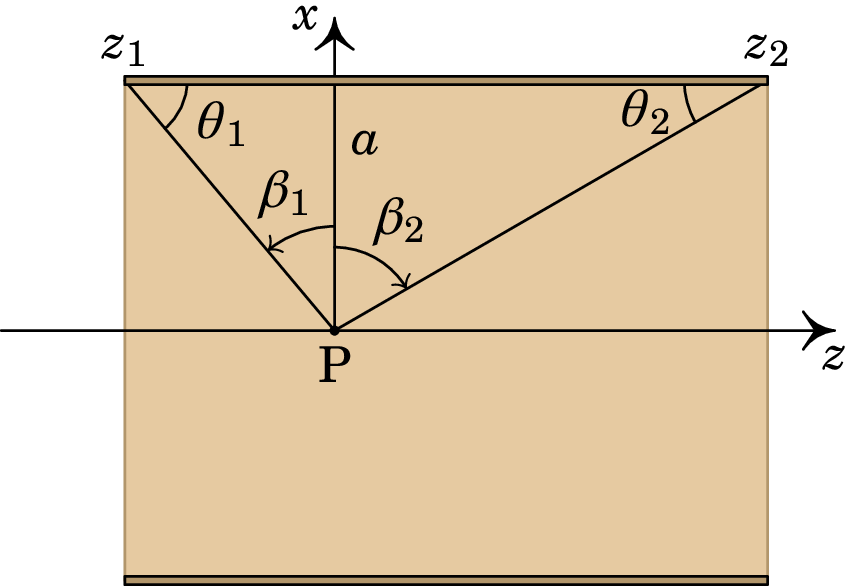
Aproximaremos o solenoide por uma distribuição contínua de espiras circulares, cada uma com centro no eixo do solenoide, com coordenada , que pode ter qualquer valor entre um valor mínimo e um valor máximo . O centro da espira na posição encontra-se a uma distância do ponto P e, usando o resultado do exemplo 8.3, o campo que essa espira produz em P é dado pela expressão:
Num intervalo infinitesimal passam espiras, onde é o número de espiras por unidade de comprimento. O campo que essas espiras produzem no ponto P é na direção de e com valor igual a:
Integrando esta expressão entre os valores mínimo e máximo de :
Usando a mesma substituição trigonométrica do exemplo 8.1,
em que varia entre e (ver figura acima), o resultado do integral conduz à seguinte expressão:
Em função dos ângulos e da figura acima, , e o campo magnético ao longo do eixo do solenoide é:
Explicitando a expressão do exemplo anterior para um ponto situado no eixo do solenoide, o módulo do campo magnético nesse ponto é dado por (verifique):
| (8.10) |
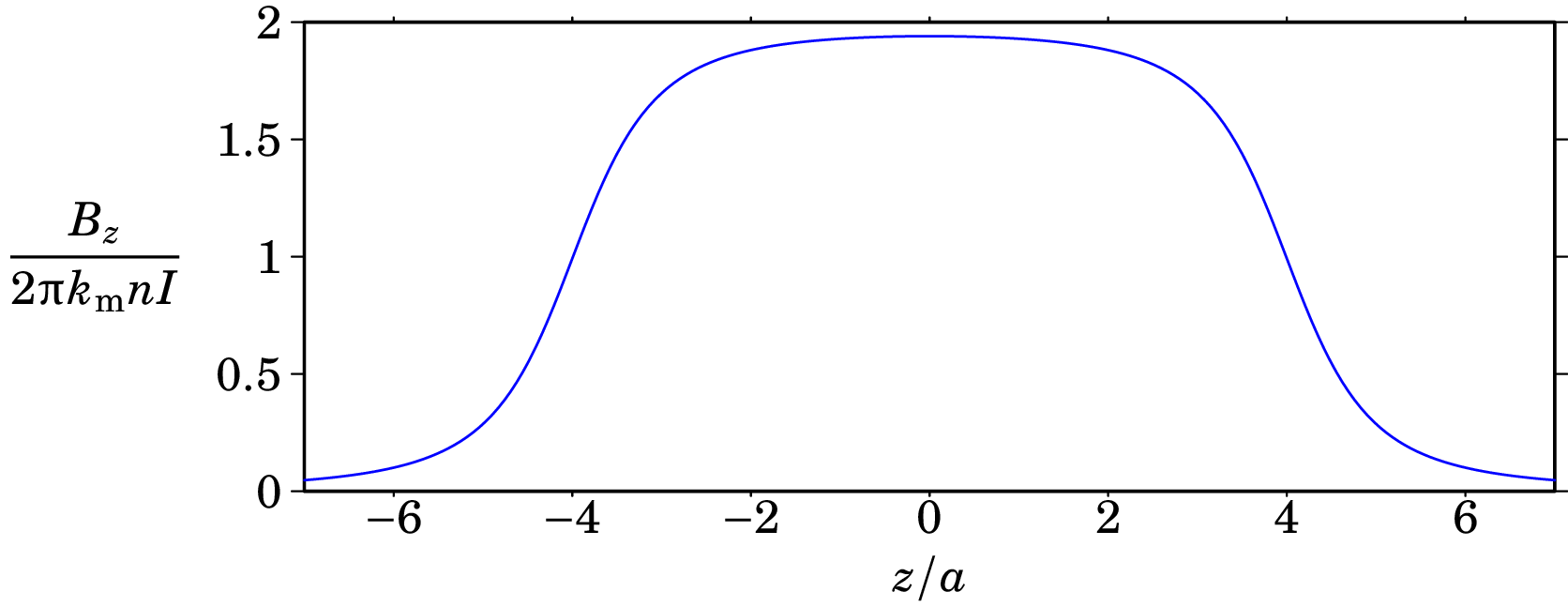
A figura 8.10 mostra o gráfico do módulo do campo magnético ao longo do eixo do solenoide, obtido no exemplo anterior, no caso de um solenoide de raio e comprimento . Para tal, usou-se e na expressão (8.10). Dentro do solenoide o módulo do campo é aproximadamente constante, aproximadamente igual a e fora do solenoide diminui rapidamente até zero. As linhas de campo são aproximadamente paralelas dentro do solenoide mas afastam-se fora dele (ver figura 8.11).
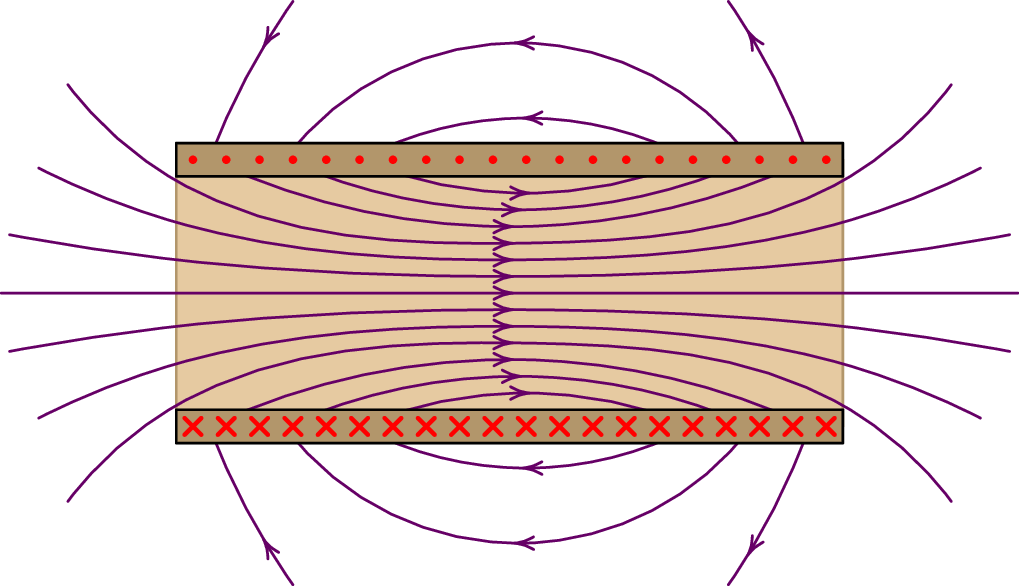
A figura 8.11 mostra o corte de um solenoide com um plano que passa pelo seu eixo e as linhas de campo magnético. As setas a sair do plano da figura (representadas por um ponto ) indicam a corrente que sai por um lado das espiras e as setas para dentro da figura (representadas por um x) indicam a corrente que entra pelos lados opostos dessas espiras. As linhas de campo que entram no solenoide aproximam-se umas das outras, até ficarem mais próximas no centro do solenoide, e depois começam a afastarem-se umas das outras quando saem do interior do solenoide. Na superfície externa do solenoide saem linhas num lado do solenoide, afastando-se entre si até ficarem mais afastadas no plano que corta o solenoide ao meio e depois aproximam-se entre si.
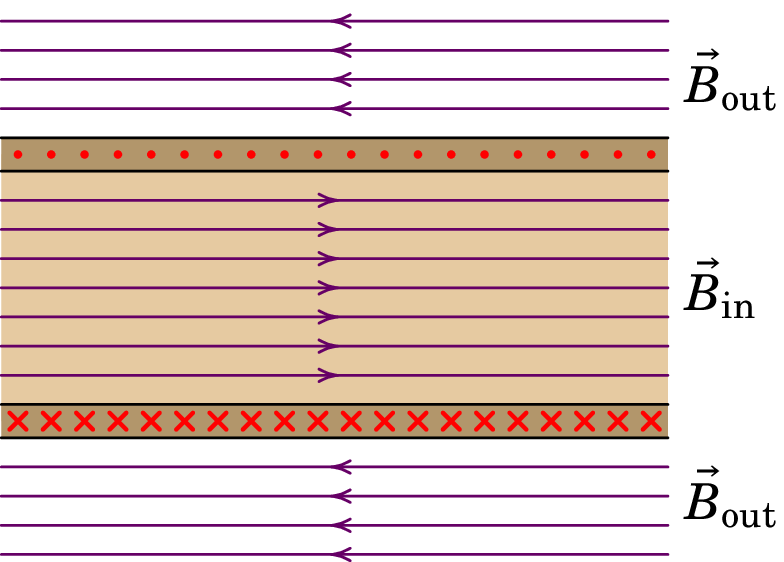
No caso de um solenoide com comprimento infinito, as linhas de campo deverão ser então paralelas dentro e fora do solenoide, tal como na figura 8.12. Como mostraremos na secção 8.6, linhas de campo magnético paralelas, num região onde não existe corrente, implicam um campo uniforme. Como tal o campo magnético dentro do solenoide infinito é uniforme, na direção axial e no sentido da regra da mão direita segundo o sentido da corrente. Fora do solenoide, o campo magnético também é uniforme e na direção axial, mas no sentido oposto do campo interno .
Como o campo a uma distância infinita do solenoide deverá ser nulo, conclui-se que o campo fora do solenoide é nulo. Para determinar o módulo do campo no interior, basta usar o resultado do exemplo 8.4 no limite em que os dois ângulos e se aproximam de zero; o resultado obtido é:
| (8.11) |
Vemos assim que um solenoide possui um campo magnético muito mais intenso no seu interior do que no seu exterior. No limite em que o solenoide é infinito o campo está todo dentro deste. O solenoide como que captura o campo magnético no seu interior. Este efeito está em analogia com o que fazem os condensadores em relação ao campo elétrico, capturando-o dentro das suas armaduras, tal como vimos na secção 4.8.
8.5 Força magnética entre fios paralelos com corrente
A figura 8.13 mostra o corte transversal de dois fios retilíneos e paralelos, com correntes e em sentidos opostos. Vamos considerar que os fios possuem comprimentos muitíssimo maiores do que a separação entre eles de modo a podermos aproximá-los por fios retilíneos infinitos. O fio da esquerda, com corrente , produz linhas de campo circulares, com centro no fio, no sentido horário. No ponto onde se encontra o fio da direita, o campo produzido pelo primeiro fio aponta para baixo e tem módulo (equação (8.3)),
| (8.12) |
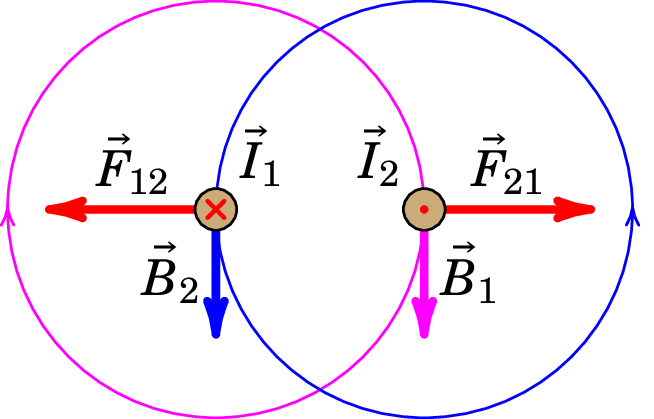
Esse campo produz força magnética no segundo fio. A força por unidade de comprimento que atua no segundo fio é, de acordo com a equação (7.40) é igual a:
| (8.13) |
que é perpendicular ao fio. Os vetores e são perpendiculares e na figura 8.13 vê-se que o seu produto vetorial é na direção que se afasta do primeiro fio. Substituindo a expressão (8.12) na equação (8.13) obtém-se o módulo da força, por unidade de comprimento:
| (8.14) |
O campo magnético que o segundo fio produz no ponto onde se encontra o primeiro é,
| (8.15) |
e a força magnética do segundo fio sobre o primeiro, por unidade de comprimento, é dada pelo produto vetorial:
| (8.16) |
O resultado é uma força com o mesmo módulo de , na mesma direção, mas no sentido oposto. Como tal, e constituem um par ação-reação com módulo dado pela expressão (8.14). Quando as correntes são no sentido oposto, a força magnética entre os fios é repulsiva.
A figura 8.14 mostra os dois casos em que as correntes nos dois fios são no mesmo sentido. Nesses casos obtêm-se a mesma expressão (8.14) para a força por unidade de comprimento, mas a força é atrativa.
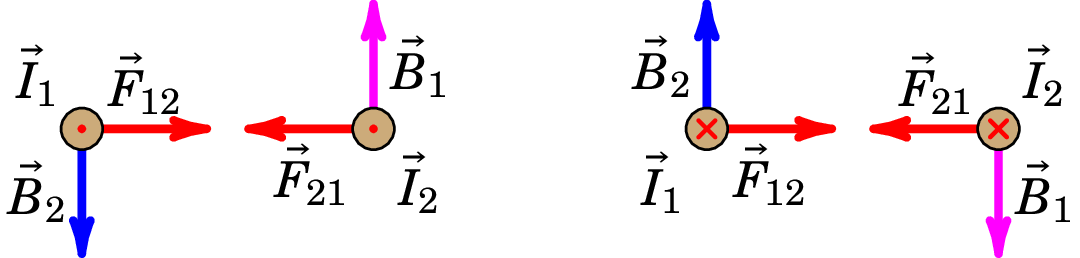
A equação (8.14) usa-se para definir o ampere no Sistema Internacional de unidades, em função do newton e do metro: um ampere é a intensidade da corrente que deve circular por dois fios retilíneos e paralelos para se obter uma força por unidade de comprimento de quando a distância entre os fios for de 1 metro.
Exemplo 8.5
Dois fios retilíneos e paralelos transportam correntes de e , no mesmo sentido, e encontram-se separados por uma distância de 5 cm (o comprimento dos fios é muito maior do que ). Calcule a força por unidade de comprimento entre os fios. Em que ponto (ou pontos) o campo magnético total é nulo?
Resolução. A força entre os fios é atrativa, e o seu módulo, por unidade de comprimento, é igual a:
Na região entre os dois fios, os campos dos dois fios têm sentidos opostos (ver figura 8.14) e, portanto, existirá um ponto P onde o campo total é nulo. Nesse ponto, os módulos dos campos das duas correntes serão iguais; usando unidades SI, temos:
onde e são as distâncias desde cada um dos fios até o ponto P. A solução desse sistema de equações é:
O campo é nulo em todos os pontos na reta paralela aos dois fios, a 2.14 cm do fio com 3 A e a 2.86 cm do fio com 4 A.
8.6 Divergência e rotacional do campo magnético
A lei de Ampère (8.8) pode também ser escrita de forma diferencial; usando o teorema de Stokes (A.81), podemos substituir o integral de linha por um integral de superfície:
| (8.17) |
onde S é uma superfície delimitada pela curva fechada C. A corrente é a corrente através da curva C, a qual pode ser calculada integrando a densidade de corrente sobre a superfície S. Como tal, a equação anterior pode ser escrita da forma seguinte:
| (8.18) |
Para que esta equação seja válida em qualquer superfície S, orientada em qualquer direção, é necessário que o termo dentro do integral seja nulo em qualquer ponto:
| (8.19) |
A equação (8.19) é a forma diferencial da lei de Ampère e constitui uma das equações fundamentais da magnetostática, que relaciona o campo magnético em qualquer ponto com a densidade de corrente nesse ponto. Para caracterizar o campo magnético numa região não é suficiente conhecer o seu rotacional em cada ponto da região; é necessário também conhecer a divergência do campo e algumas condições na fronteira da região.
Como não existem monopolos magnéticos, não existem nunca pontos onde as linhas de campo magnético divergem em todas as direções, nem pontos onde as linhas de campo convergem de todas as direções, i.e, as linhas de campo magnéticas são sempre linhas fechadas. Isso implica que o fluxo magnético em qualquer superfície fechada é sempre nulo; o fluxo magnético que entra por uma parte da superfície é igual ao que sai pela parte restante.
| (8.20) |
Aplicando o teorema da divergência (A.75), conclui-se que, em qualquer ponto, a divergência do campo magnético é nula:
| (8.21) |
Nos pontos do espaço onde não existe corrente, o rotacional e a divergência do campo magnético são ambos nulos. Se as linhas de campo magnético forem retilíneas e paralelas, numa região onde não existe corrente, o campo deverá ser necessariamente uniforme nessa região. Para o demonstrar, seja o eixo dos na direção dessas linhas de campo paralelas; em coordenadas cartesianas, o campo pode depender das três coordenadas, mas como tem unicamente componente na direção de , a forma geral desse campo será:
| (8.22) |
Calculando a divergência de , em coordenadas cartesianas, e igualando a zero obtém-se:
| (8.23) |
que implica que não depende de . O rotacional de , em coordenadas cartesianas é igual a:
| (8.24) |
e como deve ser um vetor nulo, conclui-se que as derivadas e também são nulas e o campo não pode depender nem de nem de . O campo deve então ser constante.
O campo elétrico numa região onde não existam cargas também tem divergência e rotacional nulos em todos os pontos dessa região (equações (2.30) e (2.39)). Consequentemente, se as linhas de campo elétrico forem retilíneas e paralelas, numa região onde não existem cargas livres, o campo será uniforme nessa região. Por outras palavras, campos uniformes estáticos possuem divergência e rotacional nulos, i.e., só podem existir em regiões onde não existem nem carga elétrica nem corrente elétrica.
Até agora temos considerado unicamente campos elétrico e magnético estáticos, i.e., que não variam em função do tempo. No seguinte capítulo veremos que quando o campo magnético varia em função do tempo, o campo elétrico deixa de ser conservativo e o seu rotacional não tem de ser nulo em todos os pontos. De forma análoga, quando o campo elétrico varia em função do tempo, o rotacional do campo magnético não depende apenas da densidade de corrente, mas também da derivada do campo elétrico em função do tempo. No caso de campos não estáticos , em regiões onde não existem cargas nem correntes, é possível existirem campos não uniformes com linhas de campo paralelas (ondas eletromagnéticas planas).
Problemas
-
8.1.
A figura mostra dois fios muito compridos (i.e., podem ser considerados como infinitos) e paralelos, no plano perpendicular a eles. A intensidade da corrente em cada fio é a mesma, , mas com sentidos opostos, como indicam o ponto e a cruz x nos dois fios.
(a) Represente graficamente os vetores de campo magnético devido a cada fio e o campo magnético resultante no ponto P.
(b) Encontre a expressão do módulo do campo magnético em qualquer ponto P sobre o eixo , em função da distância de P à origem.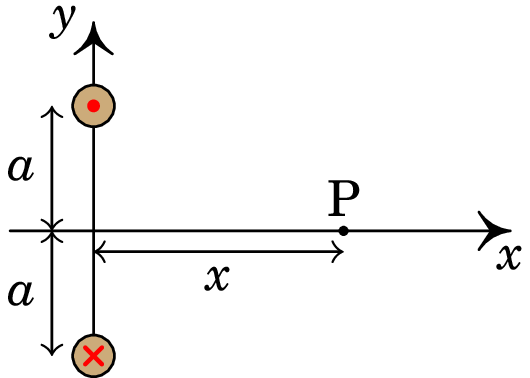
-
8.2.
Considere o fio representado na figura, composto por dois segmentos semicirculares concêntricos de raios e , percorrido por uma corrente de intensidade . Determine o campo magnético no centro P dos dois segmentos semicirculares.
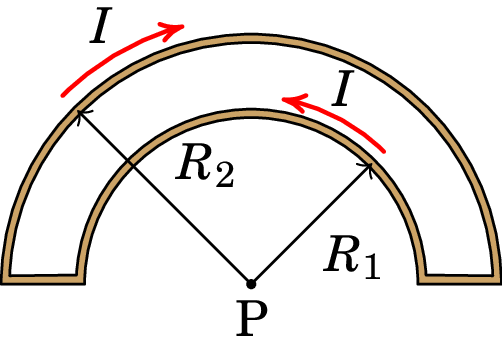
-
8.3.
A figura mostra uma bobina de Helmholtz, formada por duas bobinas circulares, cada uma de raio e com espiras, ambas com eixo no eixo , paralelas e a uma distância entre elas. A corrente é igual nas duas bobinas e circula no mesmo sentido em ambas. Com essa configuração é possível produzir campo magnético aproximadamente constante na região central entre as duas bobinas.
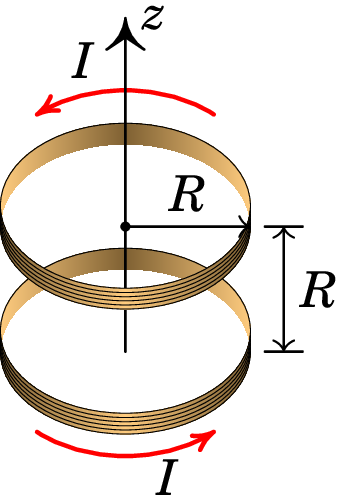
(a) Encontre a expressão do módulo do campo magnético em função de , com no ponto médio entre os centros das duas bobinas.
(b) Mostre que as duas primeiras derivadas de são nulas em .
(c) Mostre que os três primeiros termos na série de Taylor de em torno de conduzem a um valor constante. -
8.4.
Um condutor cilíndrico oco muito comprido, com raio interno e raio externo , transporta uma corrente , paralela ao eixo do condutor, distribuída uniformemente na secção transversal do condutor. Encontre a expressão do campo magnético em função da distância até o eixo do cilindro, .
-
8.5.
Um fio condutor cilíndrico muito comprido, de raio , conduz corrente de intensidade . A corrente está distribuída de forma não-uniforme, com densidade , onde é a distância até o eixo do fio e uma constante. Determine a expressão do campo magnético no interior e no exterior do fio.
-
8.6.
A figura representa três fios condutores retilíneos, muito compridos e paralelos ao eixo , com correntes no sentido positivo desse eixo.
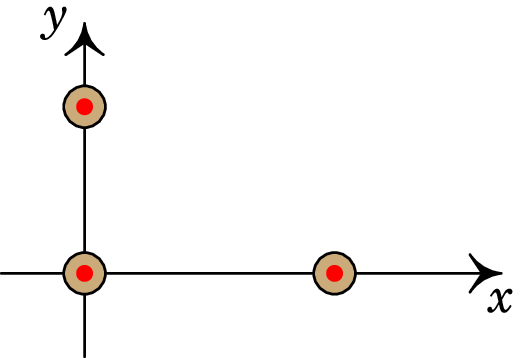
A corrente no fio que passa por (, ) = (0, 1 cm) é 0.64 A, a corrente no fio que passa pela origem é 0.63 A e a corrente no fio que passa por ponto (, ) = (2 cm, 0) é 0.43 A. Determine o módulo da força magnética resultante, por unidade de comprimento, no fio que passa pela origem.
-
8.7.
Considere dois fios de cobre, retilíneos e paralelos, de 60 cm de comprimento, distanciados de 9 cm e com raios de 2 mm e 3 mm. Calcule o valor da força magnética entre os fios quando cada um deles for ligado a uma f.e.m. de 1.5 V. (Use o valor da resistividade do cobre à temperatura ambiente: .)
-
8.8.
A figura mostra as linhas de campo magnético de um fio muito comprido com corrente, dentro de um campo magnético externo uniforme ; o fio é perpendicular à folha e os eixos e foram escolhidos sobre o plano da folha.
(a) Escreva o versor na direção do campo externo, usando o sistema de eixos dado.
(b) Escreva o versor direção da corrente no fio.
(c) Calcule e represente o vetor unitário na direção da força sobre o fio.
(d) Considerando que A e se a força sobre o fio, por unidade de comprimento, for de N/m, calcule a distância desde o fio até o ponto P.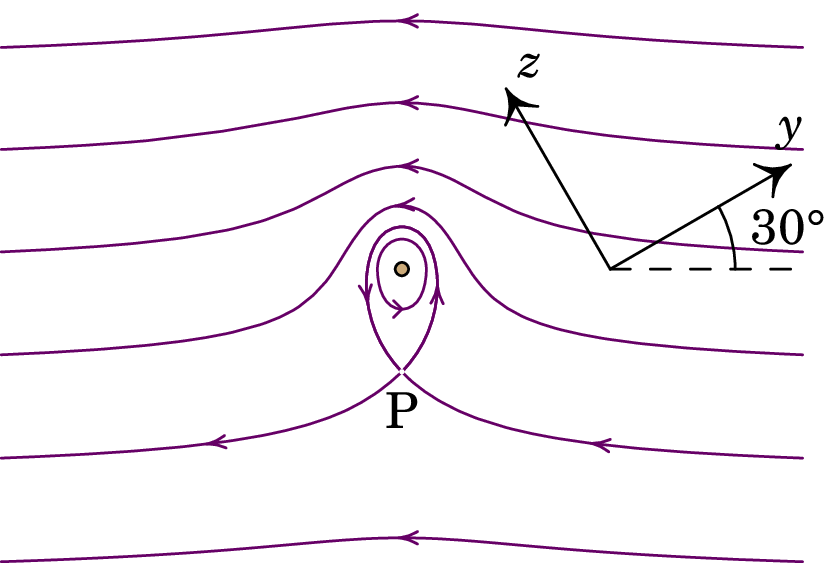
-
8.9.
Calcule o módulo do campo magnético no centro de uma espira quadrada de aresta percorrida por uma corrente .
-
8.10.
Três fios retilíneos e muito compridos, paralelos ao eixo dos , transportam correntes de 1 A, 2 A e 3 A, todas no sentido positivo do eixo dos . O fio com 1 A passa pelo ponto (2, 1) no plano (todas as distâncias em cm), o fio com 2 A passa pelo ponto (4, 2) e o fio com 3 A passa pelo ponto (2, 4). Calcule o integral de linha do campo magnético no triângulo do plano , com vértices nos pontos (3, 0), (1, 5) e (5, 3).
-
8.11.
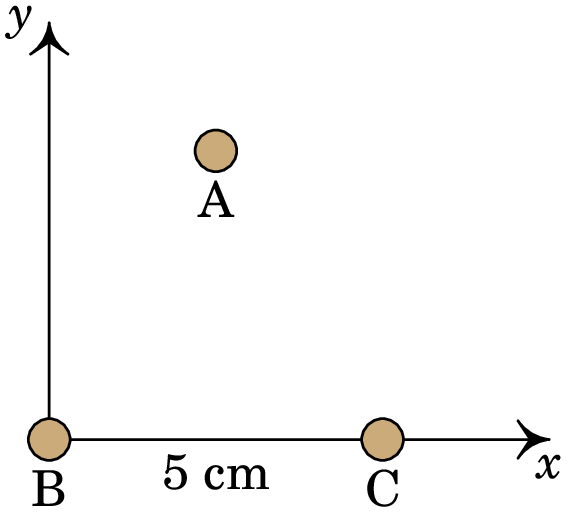
Três fios retilíneos, muito compridos e paralelos, estão dispostos de tal modo que os seus eixos formam um triângulo equilátero de 5 cm de lado conforme a figura abaixo. (a) Os fios são atravessados por corrente trifásica; no instante inicial , as correntes nos fios são: A e A. Calcule as forças, por unidade de comprimento, sobre os fios A e C.
(b) Em , as correntes nos três fios variam de forma sinusoidal segundo as expressões (unidades SI):onde é a frequência angular. Determine a expressão da força por unidade de comprimento sobre o fio A, em função de .
Nota:
e:
No capítulo 10 mostraremos como obter estas identidades. -
8.12.
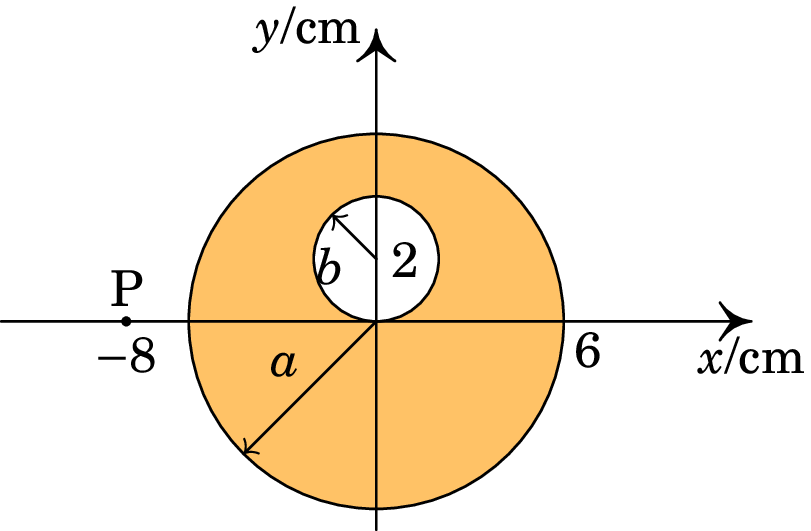
A figura representa o corte transversal de um sólido cilíndrico, muito comprido, de raio cm e com uma cavidade cilíndrica de raio cm. No cilindro flui uma corrente de densidade uniforme, , dirigida para dentro da folha de papel. Calcule o campo magnético no ponto P na posição (cm). (Sugestão: O campo será igual ao campo produzido por um cilindro maciço, de raio e centro na origem, menos o campo de outro cilindro maciço, de raio e centro no ponto (0,2).)
-
8.13.
Os dois fios representados na figura são muito compridos e cada um transporta uma corrente de 3 A. Um dos fios e o ponto P encontram-se sobre o plano , enquanto que o outro fio se encontra num plano paralelo a mas 5 cm acima deste ( cm). Calcule o valor do campo vetorial no ponto P com coordenadas m, .

-
8.14.
Um anel supercondutor de 5 cm de raio, transporta uma corrente de 4 A. Calcule o vetor de campo magnético, , no centro do anel.
-
8.15.
Exemplos de linhas de campo magnético retilíneas, que se estendem desde menos infinito até mais infinito são as linhas de campo ao longo do eixo de uma espira, de uma bobina ou de um solenoide (ver figuras 8.7 e 8.11), bem como num sistema de dois fios infinitos retilíneos e paralelos com correntes da mesma intensidade em sentidos opostos, todas as linhas de campo perpendiculares aos fios e equidistantes dos dois fios (ver figura 8.3). Nestes casos, a lei de Ampére implica que o integral de linha do campo, ao longo de uma linha de campo desde menos infinito até mais infinito, deverá ser igual a vezes a corrente total num dos lados dessa linha.
(a) Num sistema de dois fios retilíneos infinitos, paralelos ao eixo , que passam pelos pontos e com correntes de intensidade em sentidos opostos, o campo ao longo do eixo aponta na direção desse eixo, com valor (ver problema 8.8.1):mostre que o integral de , desde menos infinito até infinito, é igual a .
(b) O campo magnético de uma espira de raio , com corrente , ao longo do eixo da espira (eixo ) aponta na direção desse eixo com valor (ver exemplo 8.3):mostre que o integral de , desde menos infinito até infinito, é igual a .
(c) Num solenoide de comprimento com espiras de raio percorrido por uma corrente de intensidade , se for muito maior do que , pode-se admitir que o campo ao longo do eixo do solenoide tem valor constante dentro do solenoide e 0 fora dele, onde é o número de espiras por unidade de comprimento (expressão (8.11)). Mostre que o integral do campo magnético ao longo do eixo do solenoide é igual a .
Respostas
-
8.1.
(a)
(b)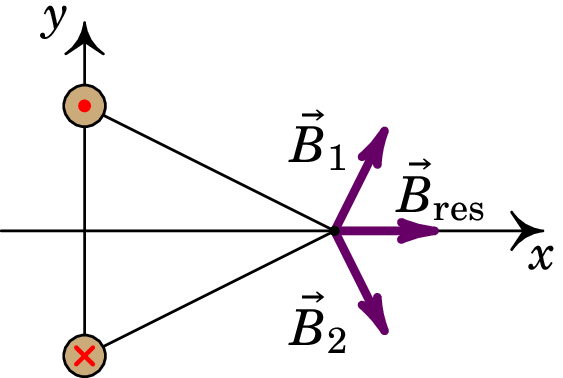
-
8.2.
para fora da folha.
-
8.3.
(a) (c)
-
8.4.
, se , , se , e , se .
-
8.5.
O campo é na direção azimutal , com módulo:
-
8.6.
8.507 µN/m.
-
8.7.
10.25 N.
-
8.8.
(a) . (b) .
(c) . (d) 2.5 mm. -
8.9.
-
8.10.
6.28 G·cm.
-
8.11.
(a) mN/m.
(b) . -
8.12.
T.
-
8.13.
nT.
-
8.14.
(µT).