4. Energia eletrostática e capacidade

Pieter van Musschenbroek (1692–1761)
Em 1745, o holandês Pieter van Musschenbroek inventou o primeiro condensador. Enquanto usava uma garrafa de vidro para isolar uma lâmina metálica no seu interior, descobriu que quando segurava a garrafa na mão, a carga elétrica que conseguia armazenar na lâmina era muito maior do que quando a garrafa estava sobre a mesa. A explicação é que na mão, que é um condutor, são induzidas cargas de sinal contrário que atraem as cargas no metal, permitindo que seja mais fácil introduzir mais cargas do mesmo sinal. Colocando uma segunda lâmina metálica por fora da garrafa, facilita-se a entrada de cargas na garrafa, podendo ser armazenadas cargas muito elevadas. O condensador de van Musschenbroek ficou conhecido como garrafa de Leiden, que é a cidade onde trabalhou. Trata-se de uma das invenções mais importantes da história da eletricidade, que permitiu acumular cargas maiores, facilitando a realização de experiências de eletrostática.
4.1 Movimento de partículas num campo elétrico
Quando uma partícula com carga se desloca entre dois pontos P e Q, numa região onde existe campo elétrico , o trabalho realizado pela força elétrica, , é dado por:
| (4.1) |
onde o integral de linha entre o ponto inicial P e o ponto final Q calcula-se ao longo da trajetória da partícula, C (figura 4.1). Mas como o campo elétrico é conservativo, o seu integral de linha não depende da trajetória C, mas apenas dos pontos P e Q, sendo igual à diferença de potencial entre esses dois pontos (equação (3.4)). Temos então que:
| (4.2) |

A expressão (4.2) mostra que o trabalho da força elétrica é independente da trajetória escolhida, dependendo apenas dos pontos inicial e final daquela. Conclui-se portanto que a força elétrica é conservativa. Tal como um campo conservativo possui uma função escalar associada, denominada por potencial, uma força conservativa possui uma função escalar associada, denominada por energia potencial. Um exemplo é a força gravítica, a qual, sendo conservativa, possui associada a energia potencial gravítica. Em geral, a energia potencial associada a uma qualquer força conservativa é obtida através da seguinte relação:
| (4.3) |
onde .
As expressões (4.2) e (4.3) permitem definir a energia potencial eletrostática de uma partícula num ponto como sendo igual à carga vezes o potencial elétrico nesse ponto:
| (4.4) |
Similarmente ao potencial elétrico, o valor da energia potencial eletrostática de uma carga num qualquer ponto está definido a menos de uma constante arbitrária. Podemos somar uma qualquer constante arbitrária ao membro do lado direito da expressão (4.4), sem contradizer a equação (4.2). Arbitrando o potencial elétrico nulo no infinito, então a a energia potencial eletrostática é também nula no infinito. Assim, tal como no caso do potencial elétrico, apenas a diferença de energia potencial eletrostática possui significado físico.
Em sistemas hipotéticos, como, por exemplo, um campo elétrico uniforme em todo o espaço, nem o potencial elétrico nem a energia eletrostática podem ser arbitrados nulos no infinito. Neste caso, arbitra-se que e sejam nulas nalgum ponto 11No caso gravítico, junto da superfície da Terra, o campo gravítico é considerado como sendo uniforme e a expressão da energia gravítica , onde é a altura de uma partícula de massa ao nível do solo, implica que foi arbitrado para ..
O trabalho da força elétrica realizado sobre uma carga pontual entre entre um ponto inicial P e um ponto final Q é portanto igual a menos a variação da energia potencial eletrostática entre esses dois pontos:
| (4.5) |
onde é a diferença de potencial elétrico entre P e Q.
A definição da energia potencial eletrostática (4.4) implica a seguinte relação entre as unidades SI de energia, carga e potencial (joule, coulomb e volt):
| (4.6) |
Outra unidade de energia bastante útil no caso da energia potencial eletrostática é o eletrão-volt (eV) definido como a energia adquirida por uma carga elementar ao passar através de uma região onde existe uma diferença de potencial de 1 V:
| (4.7) |
De acordo com a equação (4.4), partículas com carga positiva têm maior energia potencial elétrica nos pontos onde o potencial é maior, enquanto que partículas com carga negativa têm maior energia potencial onde o potencial é menor. Na figura 4.1, o potencial em P é maior do que em Q (o campo aponta no sentido em que o potencial diminui). Se a carga da partícula é positiva, a energia potencial final em Q é menor do que a energia potencial inicial em P e a trajetória na figura poderá ser resultado do movimento livre da partícula com velocidade inicial para a direita e para baixo; mas se a carga da partícula fosse negativa, a trajetória na figura só seria possível devido à ação de forças externas, para que a energia potencial final em Q seja maior do que a energia potencial inicial em P.
O teorema do trabalho-energia cinética estabelece que o trabalho realizado por todas as forças (incluindo conservativas e não conservativas) sobre uma partícula entre dois pontos P e Q ao longo de uma qualquer trajetória C é igual à variação da energia cinética, , da partícula entre os pontos extremos da trajetória:
| (4.8) |
onde . O trabalho de todas as forças pode ser dividido como o trabalho das forças conservativas, , mais o trabalho das forças não conservativas, , ao longo da trajetória C. Uma vez que, por definição, , (equação (4.3)), então a expressão (4.8) pode ser escrita como:
| (4.9) |
Se houver outras forças conservativas, para além da força elétrica, a energia potencial total será a soma de todas as energias potenciais associadas a essas forças. Observe-se que no caso da presença de forças não conservativas que realizem trabalho, o trabalho é diferente ao longo de diferentes curvas C entre P e Q. Quando este trabalho for nulo, o lado direito da equação (4.9) é igual a zero e obtemos a expressão que traduz a conservação da energia total (também designada por energia mecânica).
Quando a velocidade for muito menor que a velocidade da luz, a expressão da energia cinética da partícula é a expressão não relativista:
| (4.10) |
No caso de partículas como o eletrão, mesmo um campo elétrico não muito elevado pode conduzir a velocidades onde a expressão não relativista deixa de ser válida e será necessário usar a expressão relativista. A energia de uma partícula animada com velocidade , é dada pela expressão relativista:
| (4.11) |
onde é a velocidade da luz no vácuo, m/s, e é o fator de Lorentz, o qual é dado por:
| (4.12) |
O fator varia entre 1 (quando ) até infinito (no limite em que se aproxima de ). Como tal, um corpo de massa com velocidade nula possui energia. Esta energia designa-se por energia em repouso e é dada por 22Note que a expressão relativista (4.13) implica que existe uma equivalência entre massa e energia.:
| (4.13) |
A energia cinética relacionada com a velocidade é então a diferença entre a energia relativista (4.11) e a energia em repouso (4.13):
| (4.14) |
Como é menor que 1, a série de potências da raiz quadrada em (4.12) conduz a que a energia cinética, expressão (4.14), seja dada pela seguinte série:
| (4.15) |
O primeiro termo da série corresponde pois à expressão não relativista para a energia cinética, expressão (4.10), a qual é válida quando a velocidade é pequena quando comparada com a velocidade da luz, i.e., quando .
Conhecida a energia cinética , o fator , usando a expressão (4.14), é dado por:
| (4.16) |
Em termos práticos, dada uma energia cinética, para determinar a respetiva velocidade, com 3 algarismos significativos, será suficiente usar a expressão não relativista (4.10) quando for menor do que e quando for maior do que usa-se a sua definição (4.12) para se obter a velocidade.
A tabela 4.1 mostra as energias em repouso de um eletrão, um protão e uma partícula macroscópica com massa de 1 grama. Mostra-se também a diferença de energia potencial gravítica numa diferença de altura de 1 m. A partir da tabela conclui-se que devemos considerar relativistas um eletrão com energia cinética da ordem dos keV (quilo eletrão-volt) ou superior e um protão com energia cinética da ordem de MeV (mega eletrão-volt) ou superior. Com partículas macroscópicas de massas em gramas ou superior podemos admitir que são sempre não relativistas pois na prática não teremos energias cinéticas tão elevadas, da ordem dos eV. A energia potencial gravítica poderá ser ignorada, comparada com a energia potencial elétrica, quando tivermos diferenças de potencial da ordem do volt ou superior, e distâncias da ordem do metro ou inferior.
| Partícula | Energia gravítica | |
| eletrão | MeV | peV |
| protão | GeV | neV |
| corpo de 1 grama | eV | eV |
A expressão (4.4) da energia potencial elétrica é sempre válida na física clássica, quer no regime não relativista (velocidades pequenas comparadas com ) quer no regime relativista (velocidades próximas de ). Isto é, não é necessário introduzir nesta expressão qualquer factor de Lorentz para ser válida nos dois regimes.
A primeira partícula elementar descoberta foi o eletrão, em 1897, enquanto J. J. Thomson estudava a descarga elétrica entre dois elétrodos dentro de um tubo de descarga. O tubo usado por Thomson (figura 4.2) era semelhante aos tubos de raios catódicos (CRT, siglas do termo inglês Cathode Ray Tube) usados até ao fim do século passado nos ecrãs de televisores. Dentro do tubo há muito pouco ar 33Nos tubos de descarga do século XIX era necessário que houvesse algum ar para que pudessem passar cargas entre os elétrodos. Nos tubos de vácuo do século XX, usava-se um cátodo muito quente que permitia a passagem de cargas até no vácuo. e duas lâminas metálicas C e A separadas, entre as quais se liga uma diferença de potencial, com maior potencial em A (ânodo) do que em C (cátodo). Observa-se um feixe que sai do cátodo para o ânodo, chamados raios catódicos, os quais já tinham sido observados em 1859.
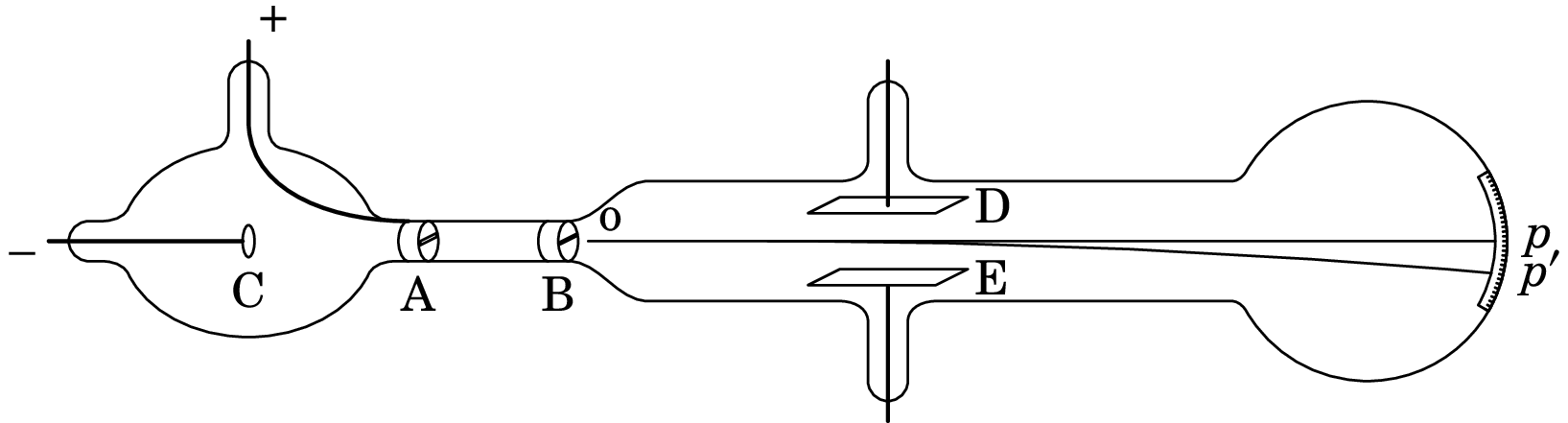
O ânodo tem uma fenda que deixa passar o feixe, o qual é de seguida alinhado por outra fenda em B, de forma a obter um feixe fino e retilíneo desde o ponto até um ponto onde o mesmo pode ser observado num ecrã.
O grande contributo de Thomson foi mostrar que os raios catódicos são formados por partículas sub-atómicas com carga negativa, todas elas com a mesma relação entre carga elétrica e massa. Para o mostrar, Thomson usou outra diferença de potencial entre duas armaduras paralelas D e E, produzindo um campo elétrico perpendicular ao feixe, o qual o desvia até outro ponto no ecrã. O sentido em que o feixe é desviado, em relação à diferença de potencial entre D e E, mostra que a carga das partículas é negativa e medindo com precisão a distância entre e em função da diferença de potencial entre D e E, Thomson obteve a relação entre a carga elétrica e a massa dos eletrões, i.e., .
Exemplo 4.1
Dentro de um tubo de vácuo há duas lâminas condutoras paralelas. Uma das lâminas é feita de um material radioativo que emite radiação beta (eletrões que são ejectados dos núcleos atómicos devido ao decaimento radioativo dos mesmos). Para acelerar as partículas até à outra lâmina, liga-se uma diferença de potencial de 150 V entre as lâminas. Num dado instante é emitida uma partícula beta com velocidade inicial de módulo 300 m/s que é acelerada até a outra lâmina. (a) Calcule o módulo da velocidade com que a partícula beta atinge a segunda lâmina. (b) Se a distância entre as duas lâminas for 5 cm, qual o módulo do campo elétrico médio entre elas?
Resolução. Como a carga da partícula beta é negativa, será acelerada na direção do potencial mais elevado; como tal, a diferença de potencial deve ser ligada de forma a que a lâmina radioativa tenha menor potencial. As linhas de campo elétrico apontam para a lâmina radioativa. A figura seguinte mostra o sistema, admitindo que campo elétrico é uniforme.
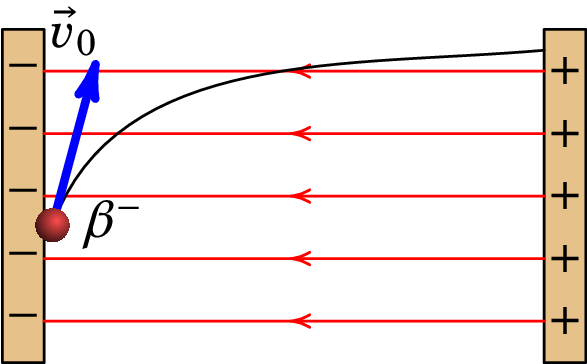
(a) O movimento da partícula beta no vácuo implica a conservação da sua energia total:
A energia potencial gravítica pode ser ignorada e a diminuição de energia potencial elétrica da partícula, na passagem entre as lâminas, é igual à sua carga (carga elementar ) vezes a diferença de potencial:
Esta energia é muito menor do que a energia em repouso de um eletrão (tabela 4.1) e como a velocidade inicial é 6 ordens de grandeza menor que a velocidade da luz, podemos usar a expressão não relativista da energia cinética.
A variação da energia cinética é então dada por:
Usando a massa do eletrão (apêndice C) e os valores da velocidade inicial e da variação da energia potencial, em unidades SI, obtém-se a velocidade final:
Note-se que não é necessário saber em que direção foi disparada a partícula e o campo não tem de ser uniforme, como na figura acima, já que apenas interessam o módulo da velocidade inicial e a diferença de potencial entre as lâminas.
(b) O campo elétrico médio, , calcula-se admitindo que o mesmo é uniforme. O integral de linha do campo, ao longo das linhas de campo e desde uma lâmina até à outra, é igual à diferença de potencial entre as lâminas:
4.2 Energia eletrostática
4.2.1 Energia de um sistema de cargas pontuais
Um sistema de cargas pontuais , ,…, nos pontos com vetores posição , , …, , tem associada uma energia potencial eletrostática que é igual ao trabalho que tem de ser realizado para colocar essas cargas nos seus pontos. Para determinar esse trabalho, consideremos que as cargas foram colocadas uma a uma nas suas posições, movendo-as com uma velocidade constante (de modo a que a sua variação de energia cinética seja nula) desde o infinito até às suas posições finais, começando por e terminando com .
A primeira carga pode ser colocada livremente na sua posição, sem ser necessário nenhum trabalho, já que não existe nenhum campo externo à carga . Contudo, para colocar na posição é preciso realizar um trabalho, , para contrariar a força elétrica entre as duas cargas, , que sente devido a , o qual é igual ao simétrico do trabalho realizado pela força elétrica desde o infinito até à posição , obtido através da expressão (4.5), e portanto, dado pelo produto da carga vezes o potencial que esta sente devido a , expressão (3.2), na sua posição .
Note que a energia potencial eletrostática da carga no infinito é nula, uma vez que o potencial de uma carga pontual foi arbitrado como sendo zero no infinito.
Este procedimento conduz portanto ao seguinte resultado:
| (4.17) |
onde é distância entre os pontos com vetores posição e .
Para trazer a terceira carga até à terceira posição, o trabalho total será a soma do trabalho, , para contrariar a força elétrica devida a , mais o trabalho, , para contrariar a força elétrica devida a :
| (4.18) |
Continuando assim até à carga , obtém-se o seguinte somatório, o qual é igual à energia potencial eletrostática armazenada no sistema de cargas pontuais:
| (4.19) |
O fator 1/2 é porque na última expressão cada termo aparece duas vezes, quando e , e quando e .
Exemplo 4.2
Um cristal iónico, tal como o cloreto de sódio (sal de cozinha), pode ser descrito por uma rede cristalina em que os iões positivos (Na) e os iões negativos (Cl) estão-se distribuídos alternadamente numa estrutura geométrica repetitiva. O lado esquerdo da figura seguinte mostra a estrutura cristalina do NaCl. Como os iões têm uma forma bastante esférica e simétrica, e a força elétrica entre esferas simétricas é igual à força entre cargas pontuais, pode-se admitir que o cristal é um conjunto de cargas pontuais colocadas tal como mostra o lado direito da figura, onde é a distância desde cada ponto da rede até os outros 6 pontos mais próximos. Determine a energia potencial eletrostática do cristal, em função da constante de Coulomb , de e do número de iões .
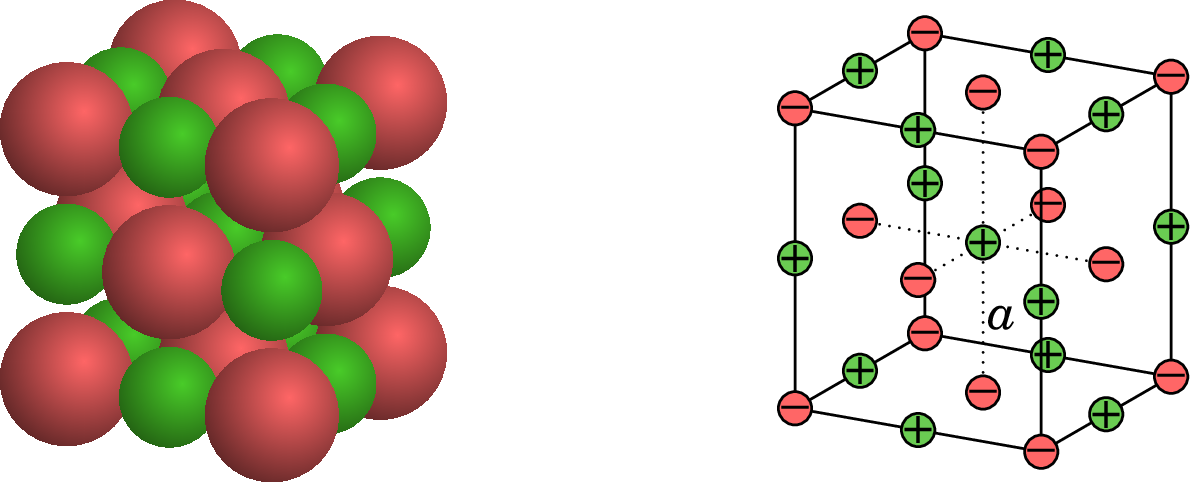
(Exemplo retirado de Purcell 1985, pág. 14.)
Resolução: Numa amostra de apenas umas gramas existirá um número muito elevado de iões e, como tal, podemos admitir que um ião qualquer, com carga está no centro, como o ião positivo no centro do cubo no lado direito da figura, e calcular a energia potencial desse ião com todos os outros iões de cargas , …, .
Escolhendo um outro ião e calculando a sua energia potencial com todos os outros iões obtém-se o mesmo resultado. Assim, a energia total será vezes a energia calculada para o ião de carga no centro. e em vez de dois somatórios da equação (4.19) teremos apenas um:
Note-se que não interessa se o ião no centro do cubo seja positivo, como na figura, ou negativo; trocando todos os sinais no lado direito da figura obtém-se um sistema equivalente, com a mesma energia. A carga do ião positivo no centro é a carga elementar , igual para todos os outros iões positivos, e a carga dos iões negativos é . A soma para , desde 2 até , convém ser feita começando pelas cargas mais próximas de , que são as que produzem um termo maior.
Para calcularmos a soma devida às 26 cargas mais próximas de , no cubo de aresta no lado direito da figura, observe-se que com origem em e eixos coordenados paralelos às arestas do cubo, as 26 cargas estão nas 26 posições com cada coordenada , ou igual a 0, ou (excluindo o caso em que , o qual corresponde ao ião no centro).
As cargas mais próximas de , são as 6 cargas que se que se encontram no centro das faces do cubo, correspondem às coordenadas em que duas delas são zero e a outra igual a , possuem carga e encontram-se à distância do centro. As seguintes cargas mais próximas, são as 12 cargas que se encontram nas arestas do cubo, correspondem às coordenadas em que uma delas é zero e as outras duas iguais a , possuem carga e encontram-se à distância do centro. A seguir, vêm as 8 cargas que se encontram nos vértices do cubo, cujas coordenadas são iguais a , possuem carga e encontram-se à distância do centro.
A energia potencial considerando a soma destes 26 termos é então:
Esta expressão pode ser escrita da seguinte forma (verifique!):
sendo necessário lembrar que o termo deve ser excluído da soma.
A vantagem desta última expressão é que pode ser facilmente generalizada de modo a incluir tantas cargas afastadas do centro quantas as que se queiram. O resultado dos 3 somatórios acima é aproximadamente igual a . Para incluir iões mais afastados, basta substituir os limites dos 3 somatórios de até por até (sendo um número inteiro positivo) e o cálculo para um valor dado de pode ser feito usando um programa de computador. Aumentando progressivamente o valor de observa-se que os primeiros quatro algarismos significativos dos somatórios aproximam-se de . Como tal, o resultado é
O resultado negativo para a energia elétrica do cristal no exemplo 4.2 indica que o cristal é estável. Será necessário fornecer energia para dissociar os iões positivos e negativos. Num sistema de cargas, energia elétrica negativa está associada a forças atrativas de ligação, enquanto que energia elétrica positiva implica forças internas repulsivas, como veremos na próxima secção.
4.2.2 Energia elétrica e campo elétrico
No caso de uma distribuição contínua de carga numa região R, a energia potencial eletrostática é o limite da expressão (4.19), quando se aproximar de infinito. Neste limite, as cargas pontuais e são cargas infinitesimais e nos elementos infinitesimais de volume e associados aos pontos de vetores posição e identificando todos os pontos da região, respetivamente; a distância entre os pontos é , os somatórios tornam-se em integrais de volume sobre toda a região R com carga e a energia potencial eletrostática do sistema é então dada por:
| (4.20) |
Um dos dois integrais de volume nessa expressão, e.g., o integral em , corresponde exatamente à equação (3.19) do potencial na posição e, como tal, a expressão para a energia eletrostática do sistema pode também ser escrita como:
| (4.21) |
A condição na equação (4.19) servia para excluir a energia de auto-interação das cargas que, no caso de cargas pontuais, é infinita. Na equação (4.21) já não é excluída a interação da distribuição de carga consigo própria.
A expressão (4.21) pode também ser escrita em função do campo elétrico. Usando a equação de Poisson (3.31), a carga volúmica pode ser substituída na equação (4.21), obtendo-se o resultado,
| (4.22) |
Em função do campo elétrico, e aplicando o teorema da divergência ao último termo,
| (4.24) |
onde S é a fronteira da região R.
Se a região R for todo o espaço, o campo elétrico na fronteira S é nulo e o segundo integral também é nulo. Nesse caso, a energia total devida ao campo é o primeiro termo da equação (4.24), que pode ser escrito como,
| (4.25) |
onde t.e. significa “todo o espaço” e é a densidade volúmica de energia elétrica, no ponto de vetor posição , dada por:
| (4.26) |
4.3 Relação entre força e energia potencial elétrica
Uma vez que a energia potencial elétrica é definida a partir da força elétrica, expressão (4.3), é também possível obter a força a partir da energia potencial. Para se obter esta relação, usa-se um procedimento análogo ao efetuado na secção 3.2 do capítulo 3, na qual se demonstrou a expressão que permite obter o campo elétrico a partir do potencial elétrico, expressão (3.12), a saber:
| (4.27) |
Já vimos que colocando uma carga num qualquer campo elétrico , esta fica sujeita a uma força elétrica dada por , expressão (1.10). Equivalentemente a esta descrição vetorial, na descrição escalar do campo elétrico, vimos que colocando a carga num qualquer potencial elétrico , esta adquire uma energia potencial elétrica dada por , expressão .
Dito isto, é suficiente agora multiplicar ambos os membros da expressão (4.27) pelo valor da carga pontual , para obtermos a relação pretendida:
| (4.28) |
onde é o gradiente da função energia potencial elétrica.
A força elétrica sobre uma carga é pois igual a menos o gradiente da sua energia potencial eletrostática. Em coordenadas cartesianas, por exemplo, temos então que:
| (4.29) |
o que permite obter as três componentes da força elétrica a partir de uma única função, .
As expressões do gradiente em outros sistemas de coordenadas podem ser obtidas na sub-secção A.3.1 do apêndice A.
Atendendo às propriedades do operador gradiente, a expressão (4.28) implica também que a força elétrica aponta sempre na direção e sentido em que a energia potencial elétrica diminui mais rapidamente.
No caso de duas cargas pontuais e , considerando a primeira na origem do sistema de coordenadas escolhido e a segunda a uma distância da primeira, a energia potencial elétrica armazenada por estas duas cargas, usando o resultado (4.17), é dada por:
| (4.30) |
Note-se que a expressão (4.30) implica que a energia potencial foi arbritada como sendo nula no infinito. A energia potencial armazenada em duas cargas pontuais em função da distância entre elas está representada graficamente na figura 4.3 para os casos das cargas possuirem o mesmo sinal () ou sinais opostos ().

Inserindo a expressão (4.30) na relação (4.28) e usando coordenadas esféricas, obtemos que a força elétrica entre duas cargas pontuais e à distância uma da outra é dada por (verifique!):
| (4.31) |
Obtemos deste modo a lei de Coulomb, expressão (1.7), discutida no capítulo 1. Note que a expressão (4.31) foi obtida considerando as cargas e com vetores posição e , respetivamente. Assim, o vetor posição relativa da carga em relação à carga é , donde a distância entre as cargas é e o versor com a direção e o sentido de é o versor radial esférico . Deste modo, a força da expressão (4.31) corresponde à força que a carga sente devido à carga , i.e., a conforme a notação usada no capítulo 1.
Quando as duas cargas pontuais são do mesmo sinal, a energia potencial é positiva e diminui com o aumento da distância entre elas (ver figura 4.3) sendo portanto a força elétrica entre as cargas repulsiva. Já no caso da cargas pontuais possuirem sinais opostos, a energia potencial elétrica é negativa e diminui com a diminuição da distância entre as cargas (ver figura 4.3), sendo portanto a força elétrica atrativa. Note-se que, quer num caso quer no outro, o sistema evolui sempre de modo a minimizar a sua energia. Deste modo, usando apenas considerações de energia, conclui-se que cargas do mesmo sinal se repelem e de sinais opostos se atraem.
É importante salientar que o campo elétrico bem como o potencial elétrico associado são campos, o primeiro um campo vetorial e o outro um campo escalar, associados, do ponto de vista mais elementar, a uma carga pontual, a qual, alterando todo o espaço à sua volta, associa a cada ponto do espaço um vetor e um escalar, respetivamente. Pelo contrário, a força elétrica bem como a energia potencial elétrica não são campos, estando na sua base, associadas à interação entre duas cargas.
4.4 Capacidade elétrica
Como vimos na secção 3.8, o potencial num condutor isolado é constante em todo o condutor e diretamente proporcional à carga total nele. Define-se a capacidade elétrica do condutor como a razão entre a carga e o potencial no condutor
| (4.32) |
A capacidade não depende da carga nem do potencial, pois os dois aumentam na mesma proporção; a capacidade depende unicamente da forma geométrica do condutor e do meio dielétrico que o envolve. O potencial no condutor, , é realmente a diferença de potencial entre a superfície do condutor e um ponto no infinito, onde costuma arbitrar-se potencial igual a zero.
A carga no condutor isolado implica também energia elétrica armazenada no condutor. Como a carga distribui-se na superfície do condutor, e não dentro do seu volume, o integral de volume na equação (4.21) deverá ser substituído por integral de superfície e em vez de densidade volúmica de carga teremos densidade superficial de carga. Tendo em conta que o potencial na superfície S do condutor é constante e que o integral de densidade superficial de carga nessa superfície dá a carga total no condutor,
| (4.33) |
E usando a definição da capacidade (4.32) a energia elétrica do condutor, em função da carga ou do potencial, é
| (4.34) |
a energia elétrica do condutor é diretamente proporcional ao quadrado da carga e do potencial. Para armazenar uma carga num condutor isolado, será necessária menor energia quanto maior for a capacidade do condutor e essa carga produzirá menor potencial no condutor quanto maior for a sua capacidade.
No sistema internacional de unidades, a capacidade elétrica mede-se em farad, em homenagem ao físico britânico Michael Faraday. Um farad, representado pela letra F, é a capacidade de um condutor que, com uma carga de 1 C, tem potencial igual a 1 V:
| (4.35) |
No caso de uma esfera condutora isolada (figura 4.4), de raio e com carga , demonstrou-se no capítulo 3 que o potencial (3.22) na superfície e dentro da esfera é igual a .
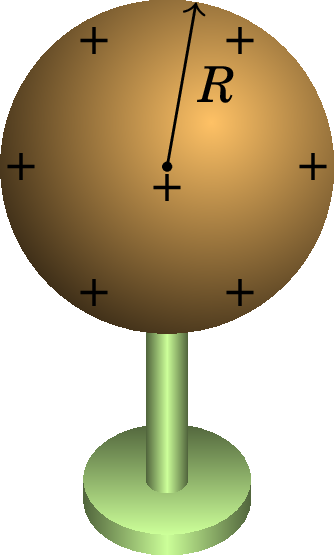
Como tal, a capacidade da esfera de raio é:
| (4.36) |
A capacidade depende apenas do raio da esfera. Quanto maior for a esfera, maior será a sua capacidade. A equação (4.36) mostra também que as unidades da constante de Coulomb são equivalentes a metro sobre farad; no cálculo de capacidades, é conveniente usar:
| (4.37) |
Por exemplo, uma esfera de um metro de raio tem capacidade de , ou seja, . A própria Terra, com raio de aproximadamente 6357 km, tem capacidade de 707 µF. Um farad é uma capacidade muito elevada; num condensador consegue-se aumentar a capacidade em várias ordens de grandeza, como veremos mais à frente neste capítulo.
Usando a relação (1.6) entre a constante de Coulomb e a permitividade elétrica do vácuo (ver apêndice C), a capacidade de uma esfera de raio rodeada por vácuo pode ser também escrita como:
| (4.38) |
Vemos assim que a capacidade de um dispositivo condutor depende do meio, neste caso o vácuo, e de fatores geométricos, neste caso o raio da esfera.
Consideremos duas esferas condutoras de raios diferentes e . De acordo com a expressão (3.22) do potencial da esfera condutora, o potencial de cada esfera é diretamente proporcional à carga nela e inversamente proporcional ao seu raio. Se inicialmente as duas esferas estão isoladas entre sim, as suas cargas e potenciais podem ser diferentes; mas se as duas esferas forem interligadas por um fio condutor, como na figura 4.5, deverá haver transferência através do fio, até que as duas esferas fiquem com cargas finais e que façam com que o potencial das duas esferas fiquem iguais, já que fazem parte de um mesmo condutor:
| (4.39) |
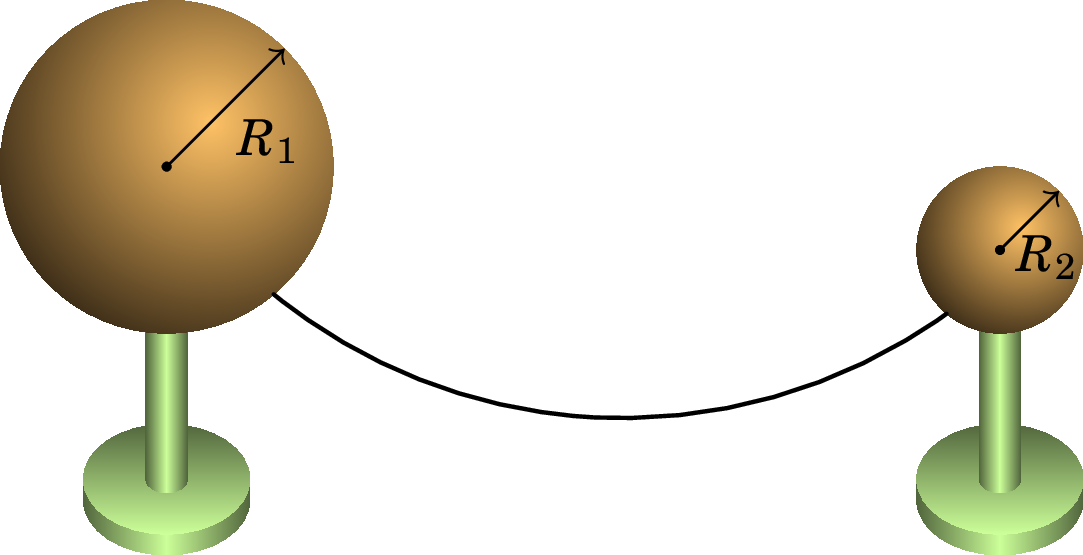
A carga distribui-se entre as esferas de forma diretamente proporcional aos seus raios. As duas cargas finais têm o mesmo sinal e por conservação da carga, a sua soma, , deverá ser igual à soma das cargas das esferas antes de terem sido interligadas, que podiam ter sinais diferentes. Apesar de a esfera maior ter mais carga, a densidade superficial de carga e o módulo do campo elétrico na superfície são menores na esfera maior.
4.5 Dielétricos
Como vimos, os materiais do ponto de vista elétrico podem ser, grosso modo, divididos em condutores e isoladores. Um dielétrico é um isolador, sem cargas de condução, em que a presença de campo elétrico induz momento dipolar no material. A maioria dos isoladores são também dielétricos.
O momento dipolar induzido num dielétrico pode ser devido a que as moléculas do material são polares, i.e., cada uma delas é um pequeno dipolo elétrico. Quando não há campo elétrico no material, esses dipolos orientam-se aleatoriamente e o momento dipolar macroscópico é nulo. O campo elétrico faz rodar os dipolos moleculares na direção do campo, produzindo momento dipolar macroscópico não-nulo (ver problema 1.14 do capítulo 1).
Existem também moléculas apolares, sem momento dipolar intrínseco, mas que na presença de um campo elétrico são deformadas produzindo momento dipolar no sentido do campo; neste caso o efeito é semelhante, embora mais fraco do que nos materiais compostos por moléculas polares. Os cristais iónicos, tal como o cristal do exemplo 4.2, sofrem também polarização devido a deslocamentos relativos dos iões positivos e negativos na rede cristalina, sob o efeito do campo elétrico (polarização iónica).
Seja qual for o mecanismo responsável pela polarização do dielétrico, na presença de um campo elétrico haverá no dielétrico muitos dipolos microscópicos com momentos dipolares alinhados na direção das linhas de campo (figura 4.6).
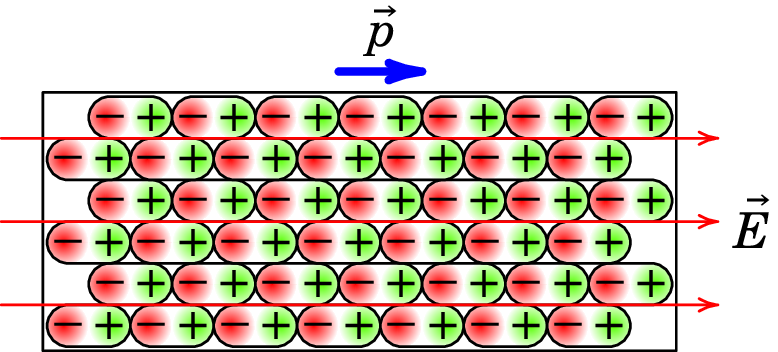
A soma dos momentos dipolares de todos os dipolos moleculares num pequeno elemento de volume dentro do dielétrico é (figura 4.7)
| (4.40) |
onde é o momento dipolar por unidade de volume; admitiremos que é uma função contínua da posição no dielétrico, chamada polarização (elétrica) do material.
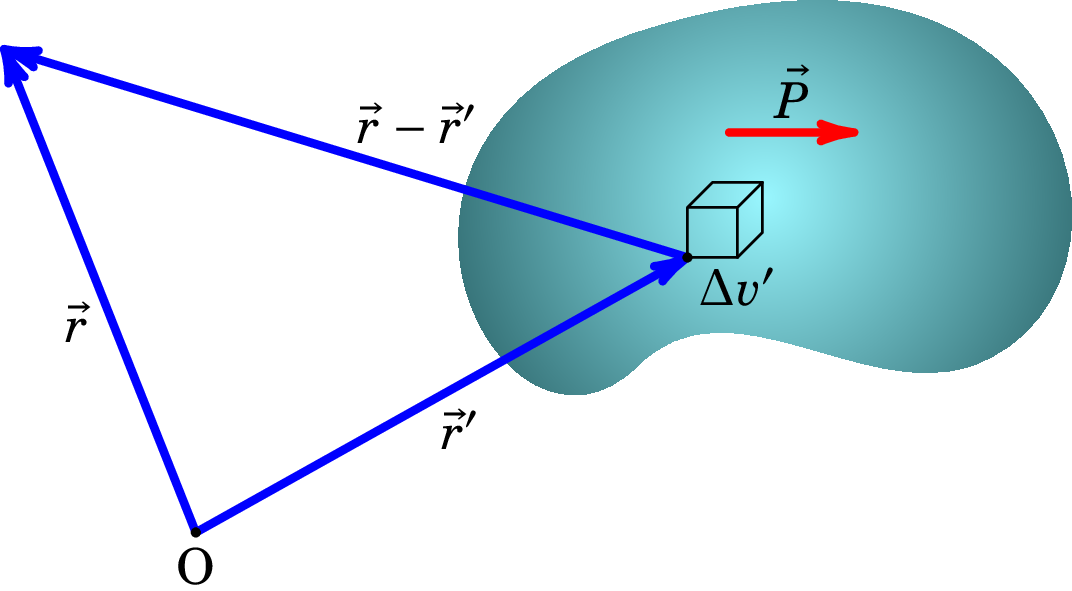
Para calcular o potencial elétrico produzido por um dielétrico polarizado num ponto exterior ao dielétrico de vetor posição , somam-se os potenciais produzidos por cada elemento de volume .
O potencial elétrico no ponto de vetor posição produzido pelo momento dipolar no volume na posição , calcula-se usando a expressão do potencial de um dipolo (3.28) com momento dipolar (expressão 4.40), no qual o vetor desde o momento dipolar até ao ponto externo é dado por , tal como mostra a figura 4.7, sendo portanto dado por:
| (4.41) |
No limite a soma dos potenciais de todas as partes do dielétrico é um integral de volume na região R ocupada pelo dielétrico e usando a equação (3.17),
| (4.42) |
onde a linha no operador indica que as derivadas são em função das coordenadas de , em vez de (por isso, o sinal negativo da equação (3.17) passa para positivo).
Usando agora a identidade (A.91) do apêndice A, para a divergência do produto do campo escalar vezes o campo vetorial ,
| (4.43) |
O teorema da divergência (A.75) permite escrever o primeiro integral como integral de superfície, na fronteira S do dielétrico:
| (4.44) |
O primeiro integral é a expressão do potencial de uma distribuição de carga na superfície do dielétrico, com densidade superficial da carga de polarização:
| (4.45) |
enquanto que o segundo integral é a expressão do potencial de uma distribuição de carga dentro do dielétrico, com densidade volúmica da carga de polarização:
| (4.46) |
No caso em que a polarização ser constante, é claro que será nula, será positiva na parte da superfície onde aponta para fora e negativa onde aponta para dentro. A figura 4.6 ajuda a compreender a origem das cargas de polarização. A orientação dos dipolos microscópicos deixa excesso de carga negativa no lado esquerdo da barra e positiva no lado direito; se os dipolos estiverem distribuídos uniformemente, não há carga total efetiva dentro da barra.
4.6 Campo elétrico no interior de dielétricos
A polarização de um dielétrico é devida ao campo elétrico que lhe é aplicado. Mas a polarização conduz a cargas de polarização que pela sua vez também produzem um outro campo elétrico dentro do dielétrico e fora deste, modificando o próprio campo responsável pela polarização. Veremos nesta secção como abordar esse problema. As cargas de polarização são ditas cargas ligadas (por oposição a cargas livres) que existem nas moléculas do material; dentro do dielétrico poderá haver também cargas livres, e.g., a carga adquirida por um dielétrico após ter sido eletrizado por condução ou por fricção. 44Livres no sentido que podem ser inseridas ou retiradas do dielétrico, mas não livres no sentido de andar livremente dentro do material, como as cargas de condução num condutor.
A figura 4.8 mostra um dielétrico com três cargas livres , e . Existe um vetor polarização no dielétrico devido ao campo elétrico produzido pelas cargas livres no seu interior juntamente com o campo elétrico das suas cargas de polarização mais um qualquer outro campo elétrico externo ao dielétrico.
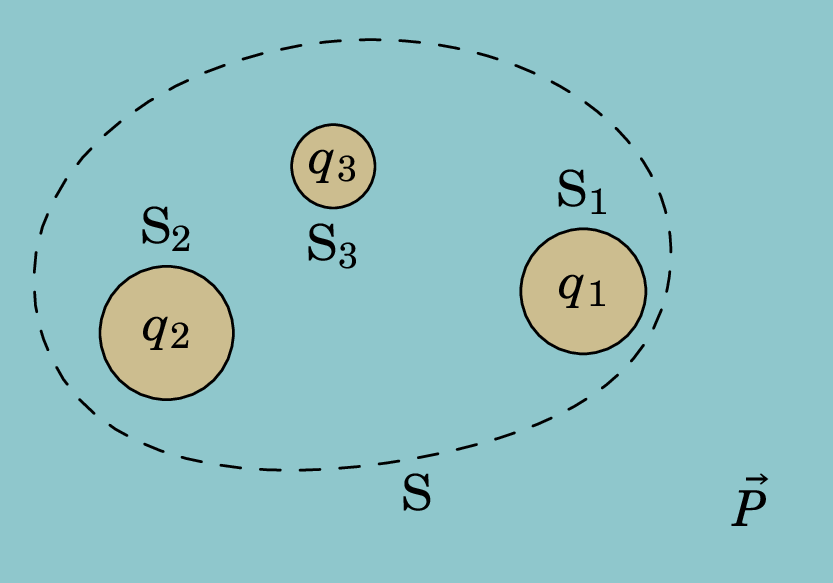
Aplicando a lei de Gauss (2.20) à superfície fechada S da figura 4.8 que envolve as três cargas livres,
| (4.47) |
onde é a soma das três cargas livres e é a carga de polarização total dentro de S. Para calcular é preciso ter em conta que dentro de S existem três superfícies fechadas , e delimitadas pelas cargas livres; nestas superfícies há densidade superficial da carga de polarização (4.45), e na região R definida pelo volume de dielétrico delimitado por S, excluindo os volumes delimitados por , e , há densidade volúmica da carga de polarização (4.46). Como tal, temos que:
| (4.48) |
Aplicando o teorema da divergência, expressão (A.75), ao integral em R, o resultado são integrais de superfície em toda a fronteira de R, i.e., nas superfícies S, , e :
| (4.49) |
substituindo em (4.48), a carga de polarização num qualquer dielétrico caracterizado por uma polarização é dada por:
| (4.50) |
e substituindo na lei de Gauss (4.47),
| (4.51) |
Define-se um novo vetor de campo macroscópico, chamado deslocamento elétrico:
| (4.52) |
Inserindo a definição acima na expressão (4.51), obtemos que a lei de Gauss para o vetor deslocamento se expressa, na sua forma integral, como:
| (4.53) |
onde é a carga livre total no interior da superfície S fechada.
A expressão anterior estabelece pois que o fluxo do vetor deslocamento elétrico através de uma superfície fechada é igual à carga livre total dentro dessa superfície. Em princípio, é então suficiente conhecer a distribuição de carga livre para determinar o vetor deslocamento elétrico.
4.7 Susceptibilidade elétrica e constante dielétrica
A polarização de um dielétrico depende do campo elétrico e da própria constituição do material. A maior parte dos dielétricos são lineares e isotrópicos, o que significa que o vetor polarização é proporcional e paralelo ao vetor campo elétrico no interior do dielétrico (não ao campo elétrico aplicado exteriormente), respetivamente: 55Um exemplo de dielétrico não linear são os materiais ferroelétricos, descobertos em 1920, que podem também manter polarização permanente sem existir campo elétrico.
| (4.55) |
onde é uma constante positiva chamada susceptibilidade elétrica, uma grandeza sem unidades.
A susceptibilidade elétrica é pois uma medida da polarização adquirida, i.e., da reacção de um dado material dielétrico a um campo elétrico exterior. Uma vez que nas regiões de vácuo não existem, pela sua própria definição, meios dielétricos, temos que para o vácuo. Deste modo, para o vácuo , enquanto que para materiais dielétricos .
O deslocamento elétrico é então também proporcional e paralelo ao campo elétrico e, usando a expressão (4.52), dado por:
| (4.56) |
onde a constante é a constante dielétrica do meio dielétrico em causa, a qual é uma grandeza sem unidades característica de cada meio (ver tabela 4.2). Temos então que o vácuo possui (valor exato, por definição), enquanto que para materiais dielétricos .
| Substância | Constante | Rigidez |
| dielétrica | dielétrica | |
| Ar (pressão atmosférica) | 1.00 | |
| Óleo mineral | 2.3 | |
| Papel | 2–4 | |
| Poliestireno | 2.6 | |
| Borracha | 2.3–4.0 | |
| Vidro | 4–10 | |
| Mica | 6.0 |
(Fonte: Cheng 2014, pág. 114.)
No caso dos dielétricos lineares e isotrópicos, a forma diferencial da lei de Gauss para o campo deslocamento elétrico , expressão (4.54), conduz, usando a relação (4.56), à forma diferencial da lei de Gauss para o campo elétrico em meios dielétricos:
| (4.57) |
onde é a densidade volúmica de carga livre. Nesta equação é a constante dielétrica no meio no ponto onde está a ser calculada a divergência de . É importante referir que na derivação da expressão (4.57), se considerou que a constante dielétrica, e portanto também a susceptibilidade elétrica, não varia de ponto para ponto do material dielétrico, o que significa que o dielétrico, para além de ser linear e isotrópico, deverá também ser homogéneo.
Calculando o integral de volume nos dois lados da equação (4.57), numa região R, obtém-se,
| (4.58) |
De acordo com o teorema da divergência, expressão (A.75), o lado esquerdo é igual ao fluxo do campo na fronteira S da região R. E se o dielétrico for homogéneo na região R, nomeadamente, a constante dielétrica é constante nessa região, a constante no denominador do lado direito da equação (4.58) pode colocar-se fora do integral e o integral da densidade de carga é igual à carga livre total na região R. Assim, a lei de Gauss numa região onde há um dielétrico linear, isotrópico e homogéneo, de constante dielétrica pode escrever-se como:
| (4.59) |
onde é a carga livre total no interior da superfície S fechada.
A única diferença relativamente à lei de Gauss no vácuo, expressões (2.20) e (2.30), é o fator no denominador do lado direito das expressões. Como tal, todos os cálculos dos campos elétricos feitos no capítulo 2, admitindo que as cargas livres se encontravam no vácuo, continuam válidos num dielétrico linear, isotrópico e homogéneo, dividindo o resultado obtido no vácuo pela constante dielétrica dos diferentes meios presentes nas regiões do espaço onde se calcula o campo elétrico.
Note ainda que as expressões (2.30) e (2.20), válidas para o vácuo, são casos particulares das expressões (4.57) e (4.59) usando nestas a constante dielétrica do vácuo, .
Combinado as expressões (4.52) e (4.56), obtém-se a relação entre a polarização de um dielétrico linear e isotróprico e o campo elétrico no seu interior:
| (4.60) |
Uma vez conhecido o vetor campo elétrico, a relação dada por (4.60) permite determinar o vetor polarização e através das expressões (4.45) e (4.46), determinam-se as densidades volúmica e superficiais das cargas de polarização no dielétrico, i.e., das cargas induzidas no dielétrico.
Para além da constante dielétrica , outra propriedade característica de cada dielétrico é a sua rigidez dielétrica, que indica o valor máximo que pode ter o módulo do campo elétrico, sem haver rutura do dielétrico. Se o campo elétrico for muito forte, superior à rigidez dielétrica, a separação entre cargas positivas e negativas nas moléculas do dielétrico será tão elevada, que algumas moléculas serão quebradas, libertando cargas que permitem a passagem de cargas de condução através do dielétrico. A rutura acontece de forma brusca e, nos dielétricos sólidos, deixa fendas onde o material fica queimado e é condutor.
Num dielétrico gasoso, um exemplo típico de rutura do dielétrico é um raio. As trovoadas dão-se quando existem campos intensos entre as nuvens e os objetos na superfície da Terra. O ar é um dielétrico que não permite a passagem de cargas entre as nuvens e os objetos; quando o campo fica muito intenso, dá-se uma rutura de algumas moléculas do ar e uma descarga elétrica brusca com transferência de cargas elétricas. Após a descarga brusca da nuvem, os iões produzidos pela rutura difundem-se na atmosfera e o ar volta a ficar isolador.
A tabela 4.2 mostra os valores da constante dielétrica e da rigidez dielétrica para alguns dielétricos. Em alguns materiais a composição química pode variar e, por isso, é apresentado um intervalo de valores em vez de um valor único.
4.8 Condensadores
Na abertura do capítulo mencionou-se a garrafa de Leiden, que historicamente foi o primeiro condensador construído. Os dois condutores separados por um isolador (neste caso vidro), designam-se de armaduras.
Quando houver carga positiva numa das armaduras, será induzida carga negativa, , na outra armadura. O cálculo da energia elétrica do sistema é feito de forma semelhante à equação (4.33), mas agora integrando em duas superfícies: a superfície da armadura com carga positiva e a superfície da armadura com carga negativa,
| (4.61) |
onde é a diferença de potencial entre as armaduras do condensador. Observe-se que na armadura com carga positiva o potencial é maior do que o potencial na armadura com carga negativa.
Define-se a capacidade elétrica de um condensador como sendo:
| (4.62) |
A capacidade elétrica é uma característica de cada condensador e é sempre uma grandeza positiva. A expressão (4.62) deve pois ser entendida como .
A capacidade de um condensador é uma constante, i.e., é uma característica intrínseca de cada condensador, que não depende nem da carga nem da diferença de potencial no condensador (se varia, então varia na mesma proporção, e vice-versa), dependendo apenas de fatores geométricos das suas armaduras e do meio dielétrico entre aquelas. Como vimos, a unidade SI da capacidade elétrica é o farad (F).
Usando a capacidade elétrica, a energia potencial elétrica armazenada no condensador pode então ser escrita em função da carga armazenada na armadura positiva ou então da diferença de potencial entre as armaduras como:
| (4.63) |
Os três tipos mais comuns de condensadores (figura 4.9) são o condensador plano, em que as armaduras são dois planos idênticos e paralelos, o condensador esférico formado por duas armaduras esféricas e concêntricas de raios diferentes e o condensador cilíndrico, com duas armaduras cilíndricas coaxiais, do mesmo comprimento mas de raios diferentes.

As duas armaduras num condensador costumam estar separadas por um dielétrico. Para além de evitar que as armaduras entrem em contacto descarregando o condensador, o dielétrico serve também de suporte e conduz a mais duas vantagens muito importantes.
A primeira vantagem é que a capacidade de um condensador aumenta quando é colocado um dielétrico entre as armaduras. Como vimos na secção anterior, o campo elétrico produzido pela carga nas armaduras quando houver dielétrico, será menor em relação ao campo se entre as armaduras houver vácuo, num fator . A diferença de potencial no condensador, igual ao integral de linha do campo entre as armaduras, também diminui de um fator e, como tal, a capacidade aumenta de um fator igual à constante dielétrica . Num condutor isolado, a capacidade também aumenta num fator quando estiver inserido dentro de um meio dielétrico com constante dielétrica .
A outra vantagem de usar um dielétrico entre as armaduras, é que o dielétrico também faz aumentar o valor máximo do potencial que o condensador pode suportar sem se queimar, devido a que a rigidez dielétrica dos dielétricos usados costuma ser maior que a do ar.
Independentemente do tipo de condensador usado, nos diagramas de circuitos um condensador é representado por dois segmentos paralelos separados entre si (figura 4.10). Ao lado do símbolo costuma escrever-se o valor da capacidade, .
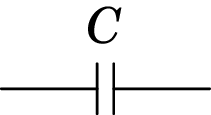
Para calcular a capacidade de um condensador, determina-se a diferença de potencial entre as armaduras quando uma delas tiver carga e a outra . Encontraremos a seguir as expressões das capacidades dos três tipos mais comuns de condensadores. Se não for referido nenhum dielétrico, admitiremos que entre as armaduras há ar, e como a constante dielétrica do ar é praticamente igual a 1, será equivalente a ter vácuo entre as armaduras.
4.8.1 Condensador plano
Um condensador plano é formado por duas armaduras iguais e paralelas, com uma forma qualquer, de área (figura 4.11). Na região central do condensador, com dielétrico de constante dielétrica , as linhas de campo são aproximadamente paralelas e, como vimos no capítulo 2, o campo de cada armadura é dado, aproximadamente, pela expressão (2.22) do plano infinito com e, devido à presença do dielétrico, tem de ser dividido por :
| (4.64) |
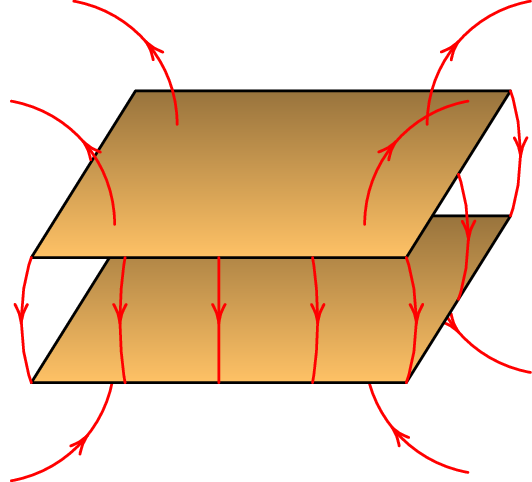
Os versores normais e são perpendiculares às armaduras com carga positiva e carga negativa, respetivamente, e apontam sempre no sentido em que se afastam da respetiva armadura.
Como tal, o campo total é nulo fora do condensador e entre as armaduras é perpendicular a elas, aponta da armadura com carga positiva para a armadura com carga negativa e possui módulo
| (4.65) |
Para calcular a diferença de potencial , pode usar-se um percurso perpendicular às armaduras, seguindo o sentido do campo: da armadura com carga positiva para a armadura com carga negativa. O resultado é,
| (4.66) |
onde é a distância entre as armaduras. A capacidade, , é então dada por:
| (4.67) |
ou, usando a relação , por:
| (4.68) |
Vemos assim que a capacidade de um condensador, neste caso plano, depende do meio dielétrico entre as suas armaduras () e de fatores geométricos das mesmas ( e ).
Exemplo 4.3
Um condensador variável é constituído por duas placas planas paralelas com forma de setor circular de ângulo 80 e raio 5 cm, que podem rodar à volta de um eixo comum, como mostra a figura. O meio dielétrico entre as placas é o ar. Se a distância entre as placas é 0.5 cm, calcule a capacidade máxima e a capacidade quando uma das placas roda 30 a partir da posição onde a capacidade é máxima. Considere que a expressão da capacidade para um condensador plano, (4.67) ou (4.68), é uma boa aproximação para o cálculo da capacidade deste condensador.
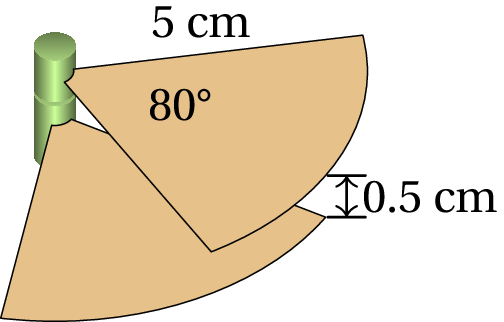
Resolução. A capacidade máxima obtém-se quando as duas placas estão uma em frente da outra, de forma que a carga se distribui ao longo de toda a superfície das placas. O ângulo de 80 é igual a radianos e a área dos setores de círculo é
A capacidade é dada pela expressão do condensador plano, e considerando a constante dielétrica para o ar, temos então que:
Quando uma das placas roda 30, a área na qual a carga se distribui, corresponde apenas à área da parte das placas que se encontra em frente uma da outra, ou seja, um setor circular de ângulo 50. Portanto a área é 5/8 da área das placas e a capacidade, sendo diretamente proporcional à área, será 5/8 da capacidade máxima:
Como vimos na secção 4.2, a energia potencial eletrostática pode ser calculada a partir da carga ou do campo elétrico. Como exemplo ilustrativo, mostraremos outra forma de obter a capacidade do condensador plano, a partir da energia elétrica armazenada, obtida a partir do campo elétrico.
Na aproximação em que as armaduras são consideradas planos infinitos, o campo elétrico tem módulo constante na região entre as armaduras, e nulo fora dessa região. Na expressão (4.26) da densidade volúmica de energia elétrica, a constante deve ser multiplicada pela constante dielétrica , devido ao dielétrico colocado entre as armaduras:
| (4.69) |
e como é constante na região entre as armaduras e nula fora dela, o seu integral de volume em todo o espaço é igual a vezes o volume dentro do condensador, e energia elétrica armazenada é:
| (4.70) |
O campo, uniforme, é igual à diferença de potencial entre as armaduras, dividida pela distância entre elas, e a energia armazenada é,
| (4.71) |
4.8.2 Condensador esférico
Este tipo de condensador é formado por duas superfícies esféricas condutoras concêntricas, com raios e (). O campo elétrico entre as duas superfícies é radial esférico (figura 4.12) e devido unicamente à superfície esférica de raio , porque no interior da superfície esférica de raio o seu campo é nulo. Se a carga na superfície esférica de raio for e na superfície esférica de raio a carga for , o campo a uma distância , entre e , do centro das esferas é dado pela equação (3.23) multiplicando pelo fator por causa do dielétrico:
| (4.73) |
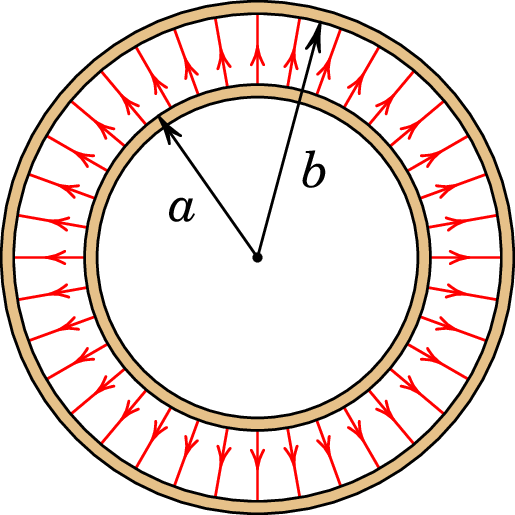
Ao longo de um percurso radial de até , o campo é paralelo ao deslocamento infinitesimal e, como tal, a diferença de potencial entre as esferas com carga positiva e a esfera com carga negativa é,
| (4.74) |
o que demonstra que é diretamente proporcional a e que a capacidade é dada pela seguinte expressão:
| (4.75) |
ou, usando , por:
| (4.76) |
Uma vez mais, observe-se que a capacidade de um condensador, neste caso esférico, depende do meio dielétrico usado e de fatores geométricos das suas armaduras.
De notar também que no limite em que o raio da armadura exterior tende para infinito, , a expressão (4.76) conduz ao resultado da capacidade de uma esfera de raio inserida num dielétrico, expressão (4.38).
No limite oposto, no qual se aproxima de , i.e., para uma distância entre as armaduras muito pequena (, ), então a expressão (4.76) aproxima-se da expressão da capacidade de um condensador plano, expressão (4.68), uma vez que, sendo , o valor é a área das armaduras esféricas.
Exemplo 4.4
Um condensador esférico tem uma superfície esférica externa de raio , sendo ar o seu meio dielétrico. Para se calcular o raio da superfície esférica interna, ligaram-se as duas superfícies a uma diferença de potencial de e mediu-se que a carga armazenada era de . Calcule o raio da superfície esférica interna.
Resolução. A capacidade do condensador é igual a
Por outro lado, a partir da expressão (4.75), e considerando a constante dielétrica para o ar, temos que:
onde é dado em metros. Resolvendo esta equação para , obtemos
4.8.3 Condensador cilíndrico
Um condensador cilíndrico é formado por duas armaduras cilíndricas coaxiais de raios e , sendo , (figura 4.13). O campo elétrico entre as armaduras não é exatamente na direção radial cilíndrica. No entanto, se o comprimento dos cilindros for muito maior que a distância entre as armaduras, i.e., , pode admitir-se que as linhas de campo na região central do condensador são paralelas e radiais cilíndricas, de modo a que exista simetria axial e, portanto, a se poder usar a expressão (2.27) obtida na secção 2.4.3 para o campo elétrico:
| (4.77) |
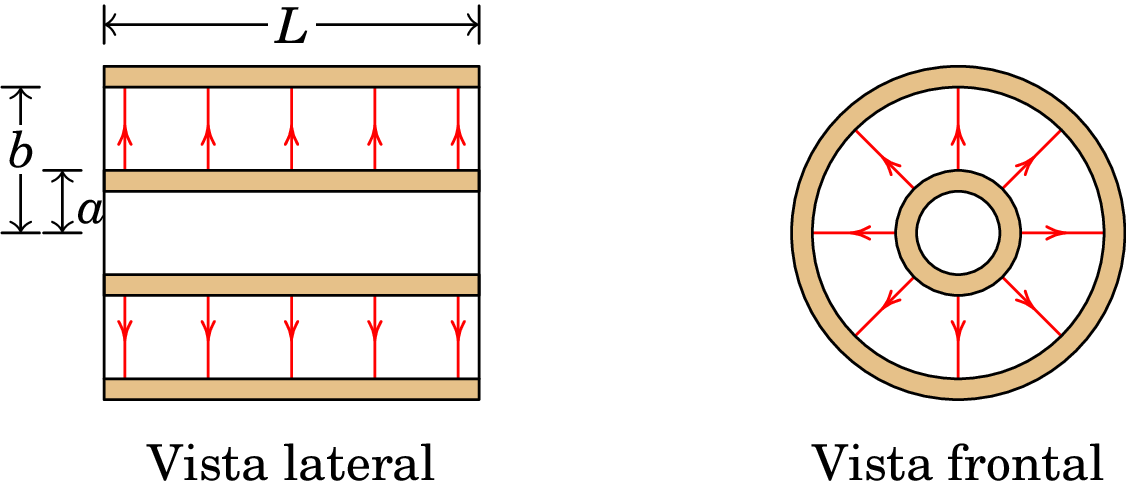
A carga dentro da superfície cilíndrica de raio e comprimento é
| (4.78) |
e substituindo na expressão do campo, temos então que:
| (4.79) |
A diferença de potencial obtém-se integrando o campo elétrico entre as armaduras, ao longo da direção radial cilíndrica:
| (4.80) |
o qual conduz à expressão da capacidade elétrica de um condensador cilíndrico:
| (4.81) |
De modo igual ao feito anteriormente, a expressão acima pode ser escrita como:
| (4.82) |
Note-se novamente que a capacidade de um condensador depende do meio dielétrico entre as armaduras e de fatores geométricos destas.
4.8.4 Ultracondensadores
Os condensadores tradicionais, considerados nas secções anteriores, a capacidade costuma ser, no máximo, da ordem dos µF. Outro tipo de condensador, chamado eletrolítico usa um dielétrico especial que permite obter capacidade superior, mas ainda aquém da ordem do farad. A expressão (4.63) implica que com diferença de potencial da ordem de 1 V, conseguem-se energias máximas na ordem do micro-joule. No capítulo 5 veremos que uma pilha pequena de 1.5 V, pode armazenar energia elétrica da ordem do quilo-joule. Um condensador com energia nessa ordem teria de ter capacidade da ordem do quilo-farad.
Uma capacidade tão elevada era algo impensável, até finais do século passado, mas hoje em dia já são construídos ultracondensadores, com capacidades na ordem dos quilo-farads e com um tamanho de apenas alguns centímetros. Nos ultracondensadores usa-se um meio poroso para substituir uma das armaduras, sendo portanto a área de contacto entre as armaduras e o dielétrico muito elevada, o que aumenta significativamente a capacidade elétrica.
Os ultracondensadores podem fornecer mais carga e serem recarregados muito mais rapidamente do que uma bateria e sem sofrer o desgaste que faz com que a bateria tenha um número limitado de ciclos de carga e descarga.
4.9 Associações de condensadores
Um sistema de condensadores pode ser substituido por um único condensador equivalente. Nos casos em que os condensadores são ligados em série ou em paralelo, é fácil calcular a capacidade do condensador equivalente.
A figura 4.14 mostra condensadores ligados em série entre dois pontos A e B, i.e., cada um a seguir ao outro, desde o ponto inicial até o ponto final.
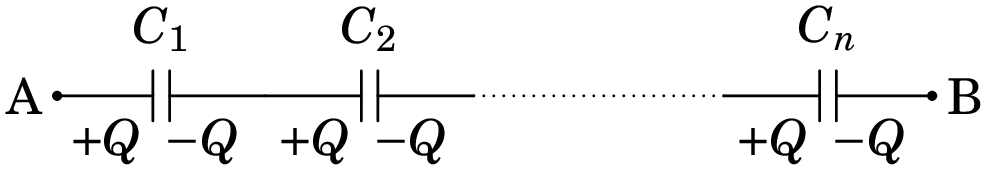
Se os condensadores estiverem inicialmente descarregados, quando se estabelecer diferença de potencial entre os pontos A e B, circulará carga que entra pelo ponto a maior potencial (A na figura) e sai pelo ponto a menor potencial. Na região que liga as duas armaduras comuns de dois condensadores vizinhos, são induzidas cargas e (carga total nula). Como tal, as cargas são iguais em todos os condensadores em série
| (4.83) |
A diferença de potencial entre A e B é a soma das diferenças de potencial em cada um dos condensadores:
| (4.84) |
O sistema é então equivalente a um único condensador com capacidade equivalente dada pela expressão:
| (4.85) |
No caso particular com apenas dois condensadores em série, a equação (4.85) conduz a . A carga armazenada no condensador equivalente é a mesma carga de cada condensador em série.
A figura 4.15 mostra um sistema de condensadores ligados em paralelo entre dois pontos A e B, i.e., cada condensador está ligado entre esses dois pontos.
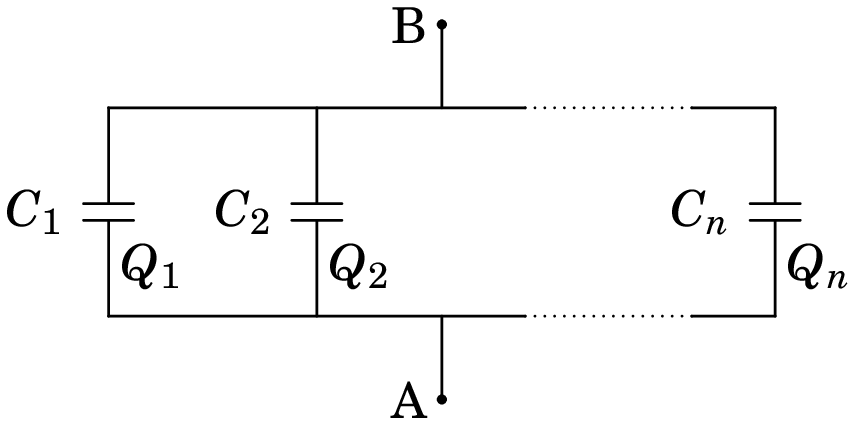
A diferença de potencial é a mesma em todos os condensadores, igual à diferença de potencial, , entre A e B
| (4.86) |
Se os condensadores estiverem inicialmente descarregados, no momento em que é estabelecida diferença de potencial entre A e B, entra carga positiva nas armaduras ligadas ao ponto com maior potencial, e sai a mesma quantidade de carga pelas armaduras ligadas ao ponto com menor potencial, mas a carga que entra em cada condensador não tem de ser a mesma. A carga total armazenada no sistema em paralelo é:
| (4.87) |
Como tal, o sistema é equivalente a um único condensador com capacidade equivalente igual à soma das capacidades dos condensadores:
| (4.88) |
Exemplo 4.5
No circuito representado no diagrama seguinte, calcule: (a) A capacidade equivalente entre A e B. (b) A carga armazenada em cada condensador quando a voltagem entre A e B for V. (c) A energia total armazenada no circuito quando V.
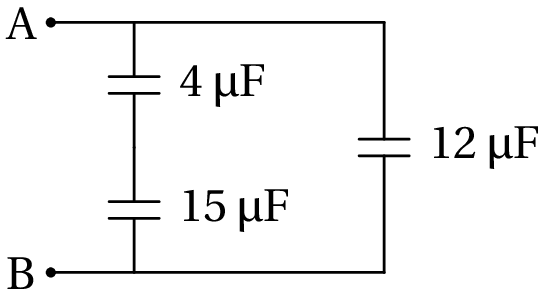
Resolução. Os condensadores de 4 µF e 15 µF encontram-se em série, podendo então ser substituídos por um único condensador de capacidade:
este condensador está ligado em paralelo com o condensador de 12 µF, pelo que a capacidade total é 15.16 µF.
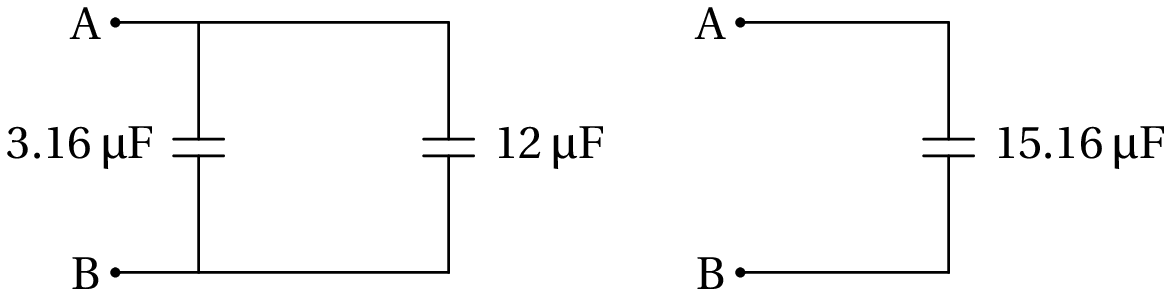
Nos dois condensadores de 12 µF e 3.16 µF a voltagem é a mesma e é igual a 200 V; como tal, as cargas nesses condensadores são:
As cargas nos condensadores de 4 µF e 15 µF são iguais porque eles estão ligados em série:
A energia total armazenada pode ser calculada somando as energias armazenadas em cada um dos condensadores; a resposta deve ser a mesma em qualquer dos circuitos equivalentes. Usando o circuito mais simples, com um só condensador de 15.16 µF, obtém-se:
Problemas
-
4.1.
Em cada caso determine a velocidade final da partícula após ser acelerada no vácuo, desde o repouso, usando a diferença de potencial dada:
(a) Um eletrão, com uma diferença de potencial de 220 V.
(b) Um eletrão num dispositivo de raios X em que é usada uma diferença de potencial de 5 kV.
(c) Um protão, no acelerador LHC (Large Hadron Collider) do CERN, em que é usada uma diferença de potencial de V. -
4.2.
Uma partícula pontual com massa de 1.5 µg e carga de 12 nC encontra-se numa região onde existe vácuo e um campo elétrico constante de módulo 2.3 kV/m com direção e sentido do eixo . Se num instante inicial a partícula estiver em repouso em cm, determine com que velocidade esta passará pela posição cm.
-
4.3.
(a) Determine a capacidade de uma esfera condutora isolada, com raio de 4.0 cm e rodeada por ar.
(b) A esfera da alínea anterior é coberta com uma camada de vidro de 1 mm de espessura e constante dielétrica de 5.6, deixando um orifício para ligar um cabo à esfera, e a camada de vidro é coberta com uma segunda lâmina metálica esférica de raio 4.1 cm, formando-se assim um condensador esférico. Determine a capacidade desse condensador.
(c) Qual a relação entre a capacidade do condensador e a da esfera? -
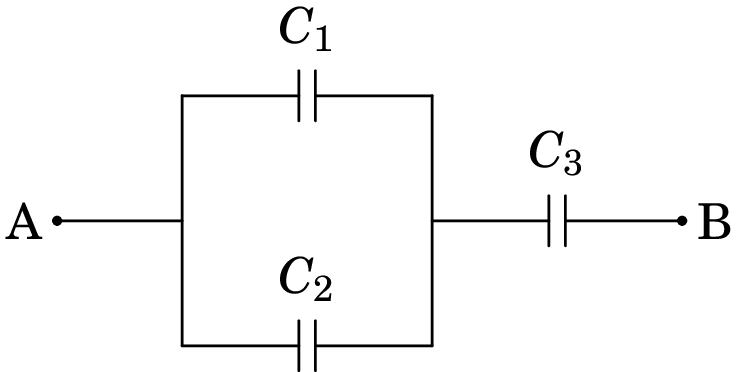
4.4.
No sistema de três condensadores apresentado na figura, µF, µF e µF. A voltagem entre os pontos A e B é de 9.0 V. (a) Determine a carga armazenada em cada condensador. (b) Determine a energia total armazenada no sistema.
-
4.5.
Uma fina barra de material dielétrico de secção reta e comprimento encontra-se no eixo entre e . Existe um campo elétrico, o qual induz na barra uma polarização dada por , onde , e são constantes. (a) Encontre a densidade volúmica da carga de polarização e a densidade superficial da carga de polarização em cada extremidade da barra. (b) Mostre que a carga total de polarização é nula, como era de esperar.
-
4.6.
No circuito da figura, calcule a capacidade equivalente: (a) Entre os pontos B e D. (b) Entre os pontos A e B.
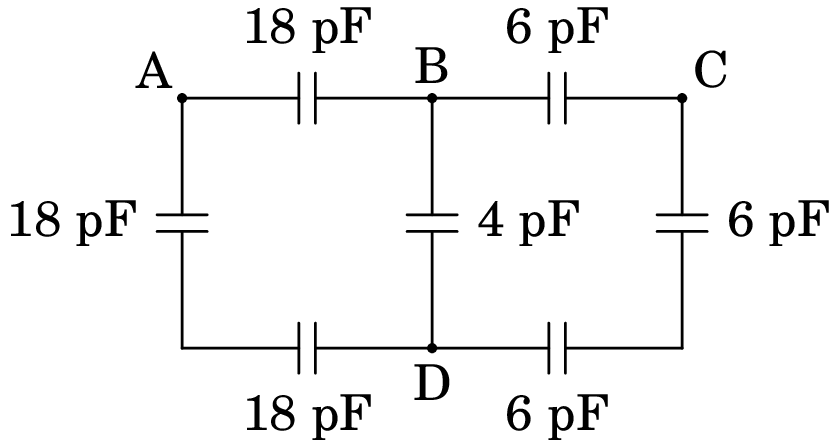
-
4.7.
Dois condensadores de 10 nF e 15 nF ligam-se em série e estabelece-se uma diferença de potencial de 3 V entre os extremos do sistema.
(a) Determine a carga e a diferença de potencial em cada condensador.
(b) Os condensadores são separados, ligando-se de seguida os dois condensadores (armadura positiva com positiva e negativa com negativa). Calcule a voltagem e a carga final em cada condensador. -
4.8.
Um condensador de 1.6 µF e voltagem máxima de 100 V liga-se em série com outro condensador de 2.5 µF e voltagem máxima de 150 V. Determine a voltagem máxima desse sistema.
-
4.9.
Descreva as quatro formas diferentes em que podem ser ligados três condensadores idênticos, cada um com capacidade de 6 nF, e em cada caso calcule a capacidade equivalente do sistema.
-
4.10.
Duas placas metálicas planas e paralelas encontram-se a 5 cm de distância e entre elas há vácuo. Entre as placas há uma diferença de potencial de 220 V. Num instante liberta-se um protão da placa com maior potencial e no mesmo instante liberta-se um eletrão na placa de menor potencial. Determine a que distância da placa de maior potencial as duas partículas se cruzam. Admita que o campo elétrico é constante e que as duas partículas partem do repouso. Considere também que o efeito da aceleração da gravidade é desprezável.
-
4.11.
Um flash fotográfico típico fornece 2 kW durante aproximadamente 2 ms. Essa energia é obtida descarregando um condensador de 50 µF.
(a) Até que diferença de potencial deverá ser carregado o condensador?
(b) Se o condensador fosse substituído por outro de 250 µF, até que diferença de potencial deveria ser carregado?
(c) Qual seria a desvantagem em usar o condensador com maior capacidade? -
4.12.
Um condensador plano possui armaduras de área , encontrando-se o espaço entre elas totalmente preenchido por dois dielétricos diferentes: um de constante dielétrica e espessura e um outro de constante dielétrica e espessura , como mostra a figura.
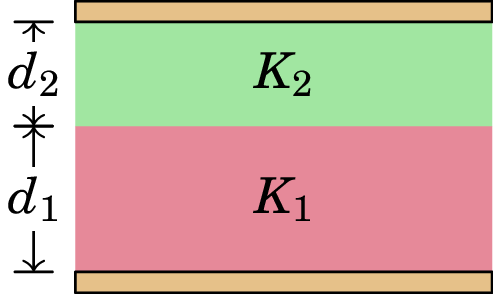
(a) Considerando a aproximação das armaduras por planos infinitos, determine o campo elétrico em cada um dos dois dielétricos, quando houver carga e nas armaduras.
(b) Integre o campo entre as armaduras para encontrar a sua diferença de potencial .
(c) Obtenha a capacidade elétrica deste condensador, a qual, de acordo com a expressão (4.62), é obtida dividindo a carga pela diferença de potencial e mostre que é igual à capacidade de dois condensadores planos em série, ambos com armaduras de área , um deles com distância entre armaduras e dielétrico de constante e o outro com distância entre armaduras e dielétrico de constante . -
4.13.
Um condensador plano tem armaduras retangulares de arestas e separadas uma distância . O espaço entre as armaduras está totalmente preenchido por dois dielétricos diferentes, um com constante dielétrica numa região de largura no lado esquerdo e o outro com constante dielétrica , numa região de largura no lado direito, como mostra a figura.
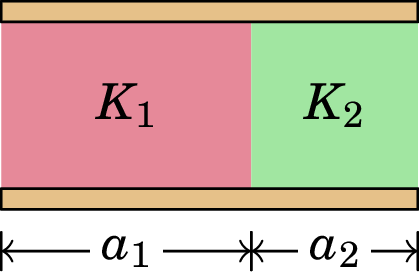
(a) Considerando a aproximação das armaduras por planos infinitos, determine o campo elétrico em cada um dos dois dielétricos, admitindo que no lado esquerdo das armaduras há cargas e e no lado direito cargas e .
(b) Integre o campo entre as armaduras para determinar a diferença de potencial em cada um dos lados, e . Como as armaduras são condutoras, a diferença de potencial nos dois lados é a mesma e igual à diferença de potencial entre as armaduras. Expresse as cargas e em função de .
(c) Obtenha a capacidade elétrica deste condensador, a qual, de acordo com a expressão (4.62), é obtida dividindo a carga total pela diferença de potencial , sendo que neste caso , e mostre que esta é igual à capacidade de dois condensadores planos em paralelo, um com armaduras de área e dielétrico de constante e o outro com armaduras de área e dielétrico de constante , ambos com separação entre as suas armaduras. -
4.14.
Considere um condensador plano, de área 0.3 m e distanciadas 0.5 cm. Entre as placas encontra-se uma chapa de acrílico com a mesma área e espessura igual a 0.5 cm. O condensador é carregado até a diferença de potencial ser igual a 12 V e, de seguida, é desligado da fonte usada para o carregar. Acrílico: e kV/m.
(a) Qual é o trabalho necessário para retirar a chapa de acrílico de entre as placas do condensador? Comente o resultado.
(b) Calcule o potencial de ruptura com dielétrico antes e depois de este ser removido. Comente o resultado. -
4.15.
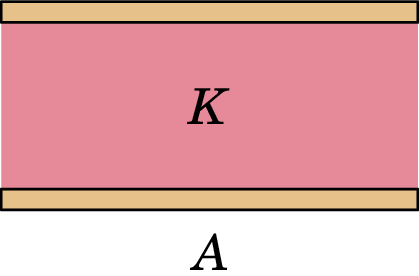
Um condensador plano, com armaduras de área e separação , está totalmente preenchido por um dielétrico de constante . Determine a carga nas duas faces do dielétrico encostadas às armaduras, bem como nas outras quatro faces laterais, em função das cargas e nas armaduras.
-
4.16.
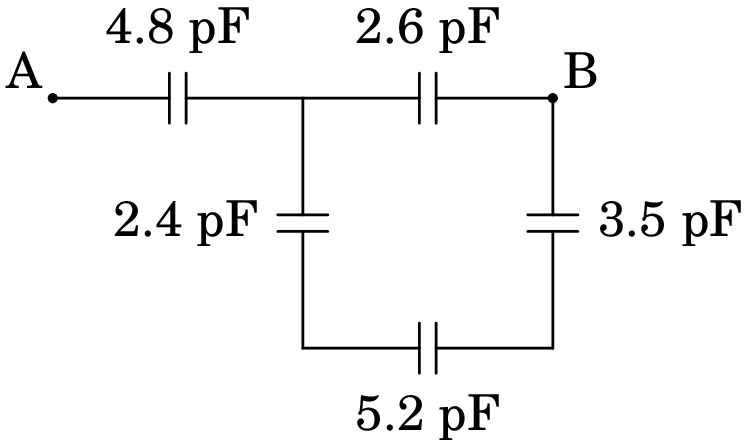
Os condensadores no diagrama seguinte encontram-se inicialmente descarregados. Calcule a carga armazenada no condensador de 2.4 pF quando a voltagem entre os pontos A e B é 5 V.
-
4.17.
As armaduras num condensador plano têm área , estão separadas uma distância e encontram-se no vácuo.
(a) Se a carga armazenada é , calcule a energia armazenada em função de .
(b) Calcule o aumento da energia eletrostática () devido a um aumento infinitesimal da distância entre as armaduras ().
(c) Calcule a força entre as placas e diga se é atrativa ou repulsiva. (Sugestão: o trabalho realizado pela força entre as placas é igual à diminuição da energia eletrostática.)
(d) Mostre que o módulo da força calculada na alínea (c) é igual a , onde é o módulo do campo elétrico entre as placas. Sabemos que a força elétrica exercida numa carga sujeita a um campo elétrico é dada por ; porque aparece o factor 1/2 no resultado anterior? -
4.18.
Considere que os dispositvos descritos a seguir se encontram rodeados por ar.
(a) Qual é a carga superficial máxima () que pode existir na superfície de um condutor isolado sem se produzir uma descarga elétrica?
(b) Qual é o raio mínimo de uma esfera metálica para que esta possa estar ao potencial de V sem se descarregar?
(c) Calcule o potencial máximo que pode alcançar uma esfera metálica de raio igual a 1 cm. -
4.19.
A capacidade de um condensador plano é normalmente calculada desprezando-se os efeitos das bordas, i.e., supondo o campo interno uniforme e o campo externo nulo. Quando se consideram os efeitos das bordas, o valor exato da capacidade é superior ou inferior a este valor aproximado?
-
4.20.
Quando o núcleo de urânio () captura um neutrão, fissiona-se em dois outros núcleos, emitindo vários neutrões que, por sua vez, podem provocar a fissão de outros núcleos. Admitindo que os produtos de fissão são núcleos com cargas iguais a e que, depois da fissão, os dois núcleos estão em repouso e separados por uma distância igual ao dobro dos respetivos raios m, calcule:
(a) A energia libertada na fissão, admitindo que esta é igual à energia potencial eletrostática dos fragmentos da fissão (o que é uma aproximação razoável).
(b) Quantas fissões por segundo são necessárias para gerar uma potência de 1 MW num reactor de urânio?
(c) Por quantos dias funcionaria o reactor da alínea (b) se tivesse uma mole de núcleos de urânio (massa atómica 238.03)? -
4.21.
Um corpo possui duas cargas concentradas em dois pontos distanciados de , constituindo assim um dipolo elétrico. O corpo encontra-se sujeito a um campo elétrico externo uniforme, . O momento dipolar tem módulo e direção e sentido da carga negativa para a carga positiva, tal como mostra a figura.
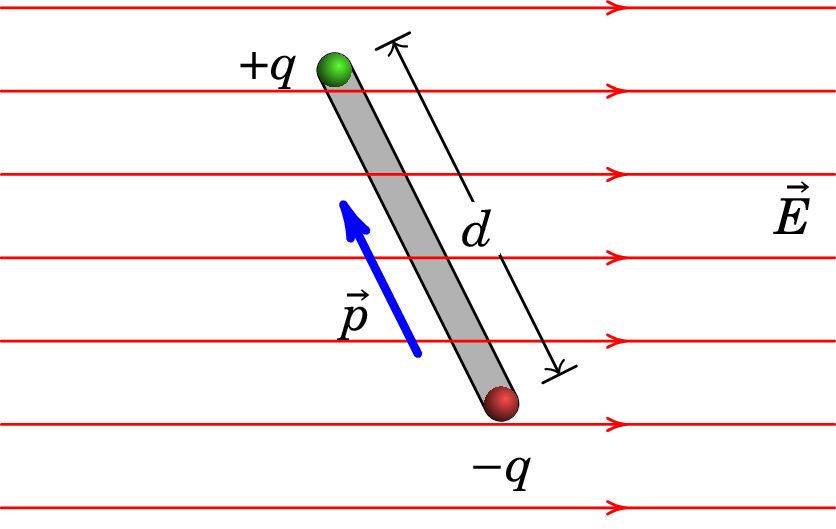
(a) Calcule o potencial elétrico associado ao campo elétrico uniforme (considere um eixo horizontal da esquerda para a direita, sendo que corresponde ao centro do dipolo).
(b) Mostre que a energia potencial eletrostática do dipolo é .
(c) Esboce o gráfico da energia em função do ângulo entre o momento dipolar e o campo elétrico externo. Para que ângulo é que a energia do dipolo é máxima e para qual é mínima? Interprete fisicamente o resultado e compare com o resultado obtido no problema 14 do capítulo 1.
Respostas
-
4.1.
(a) . (b) . (c) ( vezes a velocidade da luz!)
-
4.2.
47.0 m/s.
-
4.3.
(a) 4.45 pF. (b) 1.02 nF. (c) 229
-
4.4.
(a) µC, µC e µC. (b) 69.6 µJ
-
4.5.
(a) . Na extremidade em : . Na extremidade em : . (b) A carga total na extremidade em é , na extremidade em é e a carga total no interior da barra é .
-
4.6.
(a) pF. (b) pF.
-
4.7.
(a) nC em ambos, V no condensador de 10 nF e V no condensador de 15 nF. (b) V em ambos, nC no condensador de 10 nF e nC no condensador de 15 nF.
-
4.8.
164 V.
-
4.9.
Os 3 em série, 2 nF. Os 3 em paralelo, 18 nF. Um em série com os outros dois em paralelo, 4 nF. Um em paralelo com os outros dois em série, 9 nF.
-
4.10.
cm.
-
4.11.
(a) 400 V. (b) 179 V. (c) O condensador de maior capacidade ocupa um volume maior.
-
4.12.
(a) , (b)
(c) -
4.13.
(a) ,
(b) ,
(c)
-
4.14.
(a) nJ. Como a energia potencial do condensador aumentou, então foi transferida energia do exterior para o condesador, i.e., foi realizado trabalho sobre o condensador (). Por outras palavras, nesta situação em que a fonte é desligada e depois o dielétrico retirado, conclui-se que é preciso uma força exterior para remover o dielétrico.
(b) Sem dielétrico: 15 kV; com dielétrico: 200 kV. Devido ao aumento da rigidez dielétrica, o uso de um dielétrico entre as armaduras de um condensador, aumenta o valor máximo da diferença de potencial que um condensador pode suportar sem se queimar. -
4.15.
O dielétrico possui cargas de polarização: na face encostada à armadura com carga , na face encostada à armadura com carga e nas outras quatro faces laterais.
-
4.16.
3.15 pC.
-
4.17.
(a) . (b) . (c) , atractiva. (d) Porque para calcular a força sobre uma das armaduras há que usar o campo devido unicamente à outra armadura, que é metade do campo total .
-
4.18.
(a) 2.66 nC/cm. (b) 1/3 m. (c) 30 kV.
-
4.19.
Maior.
-
4.20.
(a) J. (b) . (c) 261.7 dias.
-
4.21.
(a) , onde .
(b) Calculam-se as energias potenciais elétricas das duas cargas, usando o resultado da alínea anterior e somam-se para determinar a energia potencial do dipolo.
(c)

A energia do dipolo é máxima para e mínima quando . De modo a minimizar a energia do dipolo, o momento dipolar roda para ficar com a mesma direção e o mesmo sentido do campo elétrico externo . No problema 14 do capítulo 1, usando forças, vimos que o dipolo fica sujeito a um binário de modo a que fica orientado segundo . Obtemos pois o mesmo efeito quer usando o conceito de força quer usando o conceito de energia, como deve ser.