1. Força elétrica

Benjamin Franklin (1706–1790)
A eletrização de objetos friccionados é um fenómeno já conhecido pelos gregos antes da era Cristã. Durante a revolução científica do século XVII, a principal área de investigação em física foi a mecânica. O estudo da eletrostática só começa no século XVIII.
Joseph Priestley publicou em 1767 uma extensa síntese de estudos qualitativos dos fenómenos eletrostáticos realizados pelos europeus Stephen Gray, Charles François Dufay e o próprio Priestley, e pelo norte-americano Benjamin Franklin, que desconhecia o trabalho dos europeus mas conhecia as teorias newtonianas da mecânica e da ótica; teorias essas que usou para interpretar as suas experiências, chegando a contribuir significativamente para o desenvolvimento da eletrostática. Entre os seus vários contributos, introduziu o termo carga elétrica e demonstrou que um raio é também uma descarga elétrica tal como as produzidas em experiências de eletrostática no laboratório.
1.1 Força e carga elétricas
Toda a matéria é constituída por átomos e cada átomo é formado por três tipos de partículas fundamentais. O eletrão foi a primeira dessas partículas a ser descoberta, por J. J. Thomson em 1897. Os outros dois tipos de partículas atómicas são os protões e os neutrões; os átomos têm um núcleo, formado por protões e neutrões, com eletrões à sua volta (ver figura 1.1). O que determina as propriedades químicas de diferentes elementos é o número de protões no núcleo, chamado número atómico.
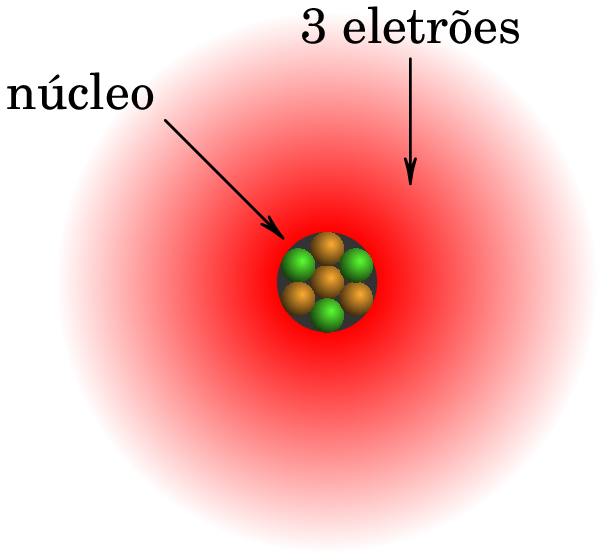
Por exemplo, o núcleo do átomo de lítio na figura 1.1, com número atómico 3, tem 3 protões e 4 neutrões e à sua volta há 3 eletrões. Um eletrão isolado é uma partícula muito pequena, mas dentro do átomo, cada eletrão assemelha-se a uma “nuvem” espalhada em torno do núcleo.
Entre dois protões ou dois eletrões atua uma força repulsiva chamada força elétrica. A origem dessa força é atribuída a uma propriedade intrínseca das partículas fundamentais, chamada carga elétrica.
A intensidade da força elétrica entre dois protões ou dois eletrões é exatamente igual, se a distância entre as partículas for a mesma. Isso implica que a grandeza da carga elétrica dos protões e dos eletrões é a mesma. Um protão e um eletrão, colocados à mesma distância que esses dois protões ou eletrões, também interagem com força elétrica da mesma intensidade, mas essa força é atrativa, em vez de repulsiva.
Conclui-se então que existem dois tipos diferentes de carga elétrica: a carga dos protões e a carga dos eletrões. A força elétrica entre duas partículas com o mesmo tipo de carga é repulsiva, enquanto que a força entre partículas com diferentes tipo de carga é atrativa.
Um átomo neutro (com igual número de protões e de eletrões) e não polarizado (nuvem eletrónica com centro no núcleo), não produz forças elétricas sobre outras partículas com carga. Como tal, convém distinguir os dois tipos de carga atribuindo-lhes sinais opostos; a convenção adotada é que a carga dos protões é positiva e a carga dos eletrões é negativa. Como o valor absoluto das cargas dessas duas partículas é igual, a carga total dos átomos com igual número de eletrões e protões é nula, explicando porque não produzem forças elétricas sobre outras partículas externas.
Quando um átomo neutro perde um eletrão, fica com uma unidade de carga positiva (ião positivo, com um excesso de um protão em relação ao número de eletrões) e produz as mesmas forças que produz um único protão. Um átomo com um eletrão a mais tem carga total igual a uma unidade de carga negativa (ião negativo, com número de eletrões igual ao seu número atómico mais um), produzindo as mesmas forças elétricas do que um único eletrão.
A unidade SI usada para medir carga é o coulomb, indicado com a letra C. Nessas unidades, a carga de um protão tem o valor exato de 11Os valores de várias constantes físicas aparecem no apêndice C. Usaremos apenas 4 algarismos significativos em todas estas constantes.
| (1.1) |
A carga de um eletrão é também igual a esse mesmo valor, mas com sinal negativo. Os neutrões não têm carga elétrica e, como tal, não sofrem nem produzem qualquer força elétrica.
A partir da segunda metade do século XX, têm sido descobertas muitas outras partículas fundamentais, mas todas essas novas partículas têm cargas elétricas iguais a um múltiplo inteiro (positivo ou negativo) do valor da carga do protão. Diz-se então que existe quantização da carga. Isto é, qualquer sistema no universo tem sempre uma carga total que é um múltiplo inteiro da carga elementar: (ver equação (1.1)).
Outra propriedade importante da carga, que tem sido observada em todas as experiências em que são produzidas ou aniquiladas partículas fundamentais, é a conservação da carga: num sistema isolado, ainda que ocorram processos de destruição e criação de partículas, a carga elétrica total é sempre constante.
1.2 Condutores e Isoladores
Os materiais do ponto de vista elétrico podem ser, numa primeira aproximação, divididos em condutores e isoladores elétricos.
Alguns materiais, designados por condutores, possuem a capacidade de conduzir corrente elétrica, i.e., de transportar facilmente carga elétrica através deles. Na origem dessa propriedade está a existência de cargas de condução que são partículas com carga elétrica que se podem deslocar facilmente por todo o material.
Um condutor pode ser sólido, por exemplo, os metais (cobre, prata, ouro, platina, alumínio, etc.). Pode também ser um líquido, por exemplo, água com sal de cozinha, em que o sal dissocia-se em iões positivos (sódio) e negativos (cloreto), os quais se podem deslocar dentro da solução. Um plasma, que é um gás com moléculas ou átomos ionizados, é também condutor.
Nos condutores metálicos um ou mais dos eletrões de valência dos seus átomos conseguem libertar-se do átomo de origem e deslocar-se por todo o metal; existe assim uma “nuvem” densa de eletrões livres, denominados por eletrões de condução, com carga negativa e com densidade constante se o material for homogéneo. Uma solução química, que pode ser sólida, líquida ou gasosa, tem igual número de cargas de iões positivos, designados por catiões, e iões negativos, designados por aniões; ambos os tipos de iões contribuem para a condução de carga através da solução. Num plasma, as cargas de condução podem ser iões positivos, iões negativos e eletrões livres.
Um material que não seja condutor diz-se isolador. Nos materiais isoladores não existem cargas livres de condução. Um isolador elétrico não possui a capacidade de conduzir corrente elétrica através dele, i.e., não transporta carga elétrica através do seu interior. Os isoladores podem ser sólidos (vidros, borrachas, a maioria dos plásticos, âmbar, materiais cerâmicos, etc.), líquidos (água destilada, hidrocarbonetos, óleo de parafina, etc.) ou gasosos (gases não ionizados).
1.3 Eletrização
Um corpo macroscópico pode apresentar três estados básicos de eletrização:
-
•
Corpo neutro e não-eletrizado: a sua carga total é nula e esta distribui-se homogenamente no corpo.
-
•
Corpo neutro e eletrizado: a sua carga total é nula, mas esta não está homogenamente distribuída, apresentando o corpo regiões com carga positiva e outras com carga negativa.
-
•
Corpo não-neutro: a sua carga total é não nula e esta pode estar ou não homogenamente distribuída.

A figura 1.2 ilustra os três casos. Usam-se símbolos e para representar regiões onde há carga positiva ou negativa, e o número de símbolos sugere a ordem de grandeza dessas cargas.
A esfera na figura 1.2 é isoladora, porque se fosse condutora, o deslocamento das cargas de condução deixaria a esfera do centro descarregada e faria com que as cargas ficassem distribuídas uniformemente na superfície da esfera do lado direito.
Existem três processos básicos de eletrização de um corpo macroscópico: fricção, condução e indução. Como veremos a seguir, os processos de fricção e de condução envolvem objetos em contacto, ocorrendo transferência de eletrões entre estes. O processo de indução entre objetos é efetuado à distância, ocorrendo redistribuição dos eletrões dentro do mesmo objeto.
1.3.1 Eletrização por fricção
É necessária uma energia muito elevada para conseguir remover um protão, ou um neutrão, do núcleo de um átomo. Isso só ocorre no interior das estrelas, na camada mais externa da atmosfera onde chocam partículas cósmicas com muita energia ou nos aceleradores de partículas onde as energias das partículas são suficientemente elevadas. Para extrair ou introduzir um eletrão num átomo neutro é necessária uma energia muito menor.
Sempre que dois objetos diferentes entram em contacto próximo, há eletrões de um dos objetos que passam para o outro. O objeto que for mais susceptível de perder eletrões fica então eletrizado com carga positiva ( protões em excesso) e o objeto que tiver menos tendência para perder os seus eletrões fica com carga da mesma intensidade, mas negativa ( eletrões em excesso). Por exemplo, a figura 1.3 mostra uma barra que perdeu eletrões após ter sido esfregada com um pano e esses eletrões passaram para o pano.
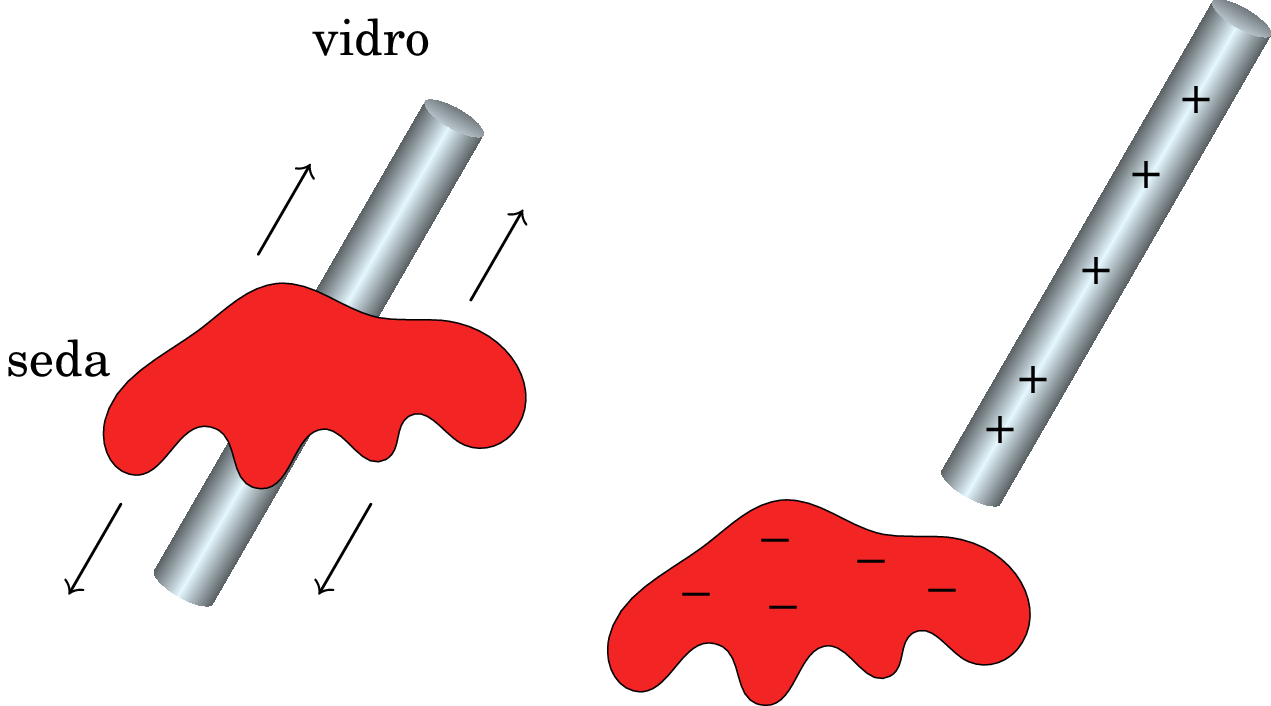
Os isoladores são mais eletrizáveis por fricção do que os condutores. Os isoladores possuem uma capacidade de condução elétrica muitíssimo baixa, o que facilita a localização da carga elétrica. Quando se eletriza um isolador por fricção, a carga (positiva ou negativa) fica localizada na região de fricção porque não consegue fluir através do isolador. Pelo contrário, os condutores possuem uma capacidade de condução elétrica elevada, o que dificulta a localização da carga elétrica. Quando se eletriza um condutor por fricção a carga não fica localizada na região de fricção mas distribui-se por todo o condutor porque consegue fluir facilmente através deste.
Os diferentes materiais podem ser ordenados numa série triboelétrica (tabela 1.1), em que os materiais no topo da série são mais susceptíveis de ficar com carga positiva e os materiais no fim da série têm maior tendência para ficar com carga negativa.
| Maior tendência a ficar com carga positiva |
| Amianto |
| Vidro |
| Lã |
| Chumbo |
| Seda |
| Alumínio |
| Papel |
| Algodão |
| Aço |
| Borracha |
| Níquel, Cobre |
| Borracha |
| Latão, Prata |
| Borracha sintética |
| Esferovite |
| Teflon |
| Maior tendência a ficar com carga negativa |
(Fonte: Tipler e Mosca 2008, pág. 695.)
Quando a barra de vidro da figura 1.3 é friccionada com seda, alguns eletrões passam do vidro para a seda, porque o vidro está acima da seda na tabela triboelétrica. Como os eletrões transportam carga negativa, o vidro fica com carga positiva e a seda com carga negativa, com o mesmo valor absoluto da carga no vidro. Se a mesma barra de vidro fosse esfregada com uma pele de animal, que está acima do vidro na série triboelétrica, a passagem de eletrões seria da pele para o vidro, ficando a barra de vidro com carga negativa e a pele com carga positiva.
1.3.2 Eletrização por condução
Quando dois objetos, estando pelo menos um deles carregado, são postos em contacto, pode ocorrer a transferência de eletrões entre ambos. Neste caso a eletrização diz-se que foi efetuada por condução.
A figura 1.4 mostra duas esferas condutoras montadas sobre suportes isoladores. Inicialmente a esfera maior tem carga positiva, a esfera menor está descarregada e as duas esferas estão separadas. A seguir as esferas são colocadas em contacto; a nuvem de eletrões de condução nas esferas desloca-se para a esquerda e para cima, deixando excesso de cargas positivas nos extremos opostos das duas esferas.
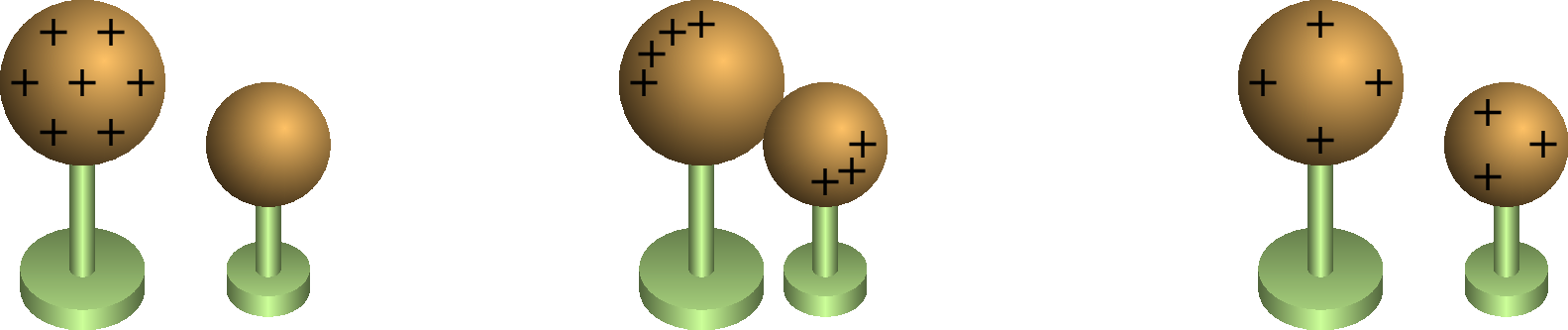
Apesar da transferência de cargas entre as esferas ser devida à passagem de eletrões da esfera neutra para a não-neutra, e as cargas positivas nos núcleos não se poderem deslocar no metal, podemos visualizar o processo mais facilmente imaginando que há cargas positivas livres numa das esferas, que se podem deslocar livremente dentro das duas esferas condutoras. As forças repulsivas entre essas cargas do mesmo sinal fazem com que se afastem ficando o mais afastadas possível.
Finalmente, as duas esferas separam-se novamente, ficando cada uma delas com parte da carga total inicial. Como será demonstrado no Capítulo 4, a carga total distribui-se entre as duas esferas de forma proporcional ao raio delas. A relação dos raios das esferas na figura 1.4 é ; como tal, se a carga inicial na esfera maior for , no fim essa esfera fica com carga e a esfera menor com carga . A soma dessas duas cargas é igual à carga inicial e a relação entre elas é . No fim, quando as esferas estão separadas, a carga em cada esfera condutora distribui-se uniformemente na sua superfície, que é onde podem ficar mais afastadas entre sim, devido à repulsão elétrica.
Pode também ocorrer eletrização por contacto simples. Quando materiais neutros diferentes são postos em contacto e depois separados, pode ocorrer uma acumulação de carga elétrica a qual deixa um material carregado negativamente e o outro carregado positivamente, ambos com cargas iguais em valor absoluto, mas de sinais opostos.
1.3.3 Ligação à terra
A partir da discussão no exemplo da secção anterior, em que uma esfera eletrizada transfere parte da sua carga para outra esfera (figura 1.4), conclui-se que se a segunda esfera fosse muito grande, a esfera inicial perdia muita mais carga. A maior esfera condutora à nossa volta é a própria Terra, que é um bom condutor por conter metais e soluções líquidas. Os objetos condutores que usamos nas nossas experiências são sempre de tamanho desprezável comparados com a Terra.
Podemos então admitir que se um condutor eletrizado for posto em contacto com a Terra descarregar-se-á ficando eletricamente neutro. O contacto com a Terra pode ser feito ligando um fio (condutor) entre o condutor carregado e o solo terrestre, i.e., efetuar o que se denomina por ligação à terra, representada pelo símbolo com quatro barras horizontais na figura 1.5.

Fisicamente o que acontece é que a carga elétrica positiva ou negativa no objeto redistribui-se por toda a superfície do sistema condutor, constituído por objeto, fio condutor de ligação à terra e o próprio planeta Terra, ficando assim o objeto praticamente neutro do ponto de vista elétrico. A Terra funciona como um reservatório “infinito” de eletrões, absorvendo eletrões do ou fornecendo eletrões ao objeto de modo a este ficar neutro.
1.3.4 Eletrização por indução
Uma outra forma de eletrizar um objeto condutor, consiste na eletrização por indução, seguida de ligação à terra. A figura 1.6 mostra uma esfera condutora, neutra, montada num suporte isolador. Inicialmente aproxima-se um objeto externo com carga, neste caso uma barra com carga positiva, que induz uma distribuição de carga positiva e negativa nos extremos opostos da esfera. Isto acontece para que a força elétrica total nas cargas de condução dentro da esfera seja nula, como estudaremos na última secção deste capítulo.
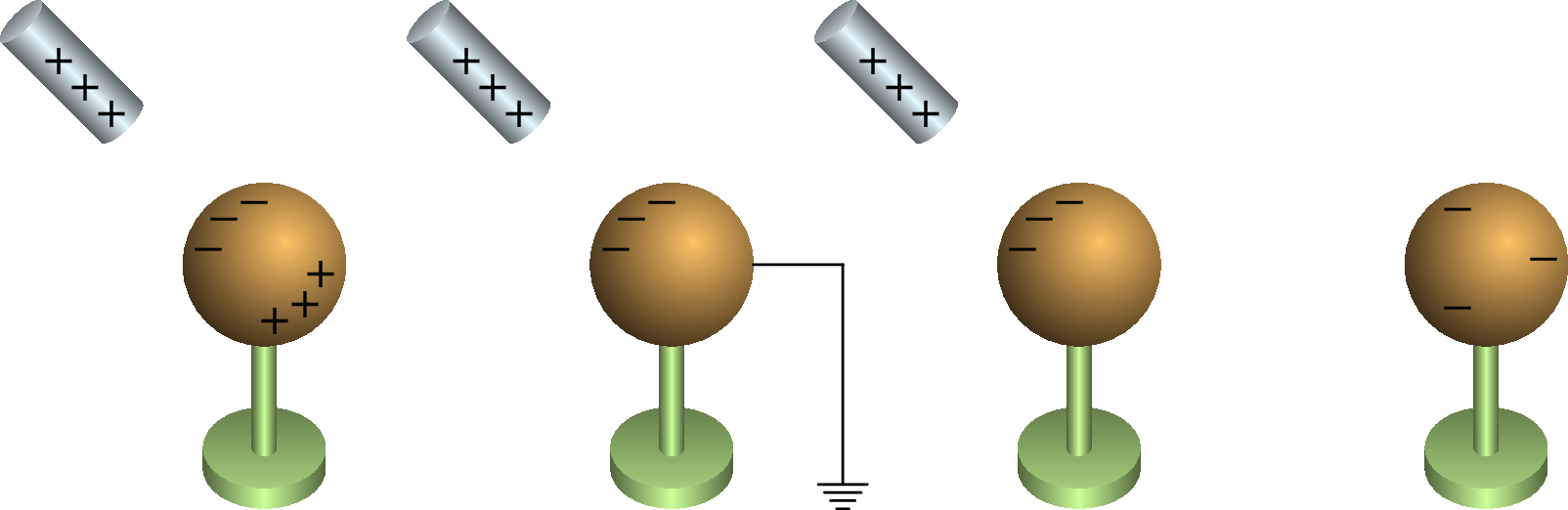
Apesar de as cargas de condução no condutor serem todas negativas, podemos também visualizar o condutor neutro como se tivesse igual número de cargas livres positivas e negativas; a barra, com carga positiva, atrai as cargas livres negativas e afasta as cargas positivas na esfera condutora.
O segundo passo na figura 1.6 consiste em ligar a esfera à terra. Neste caso as únicas cargas que passam para a Terra são as cargas positivas, repelidas pela barra com carga positiva. Apesar da ligação à terra, a esfera condutora continua carregada negativamente na zona mais próxima da barra, já que as cargas negativas estão a ser atraídas pela barra. O terceiro passo consiste em retirar a ligação à terra, ainda sem afastar a barra, e só finalmente é afastada a barra usada para induzir as cargas na esfera. Um condutor eletrizado por este procedimento fica com carga de sinal oposto ao do objeto externo usado para induzir a carga.
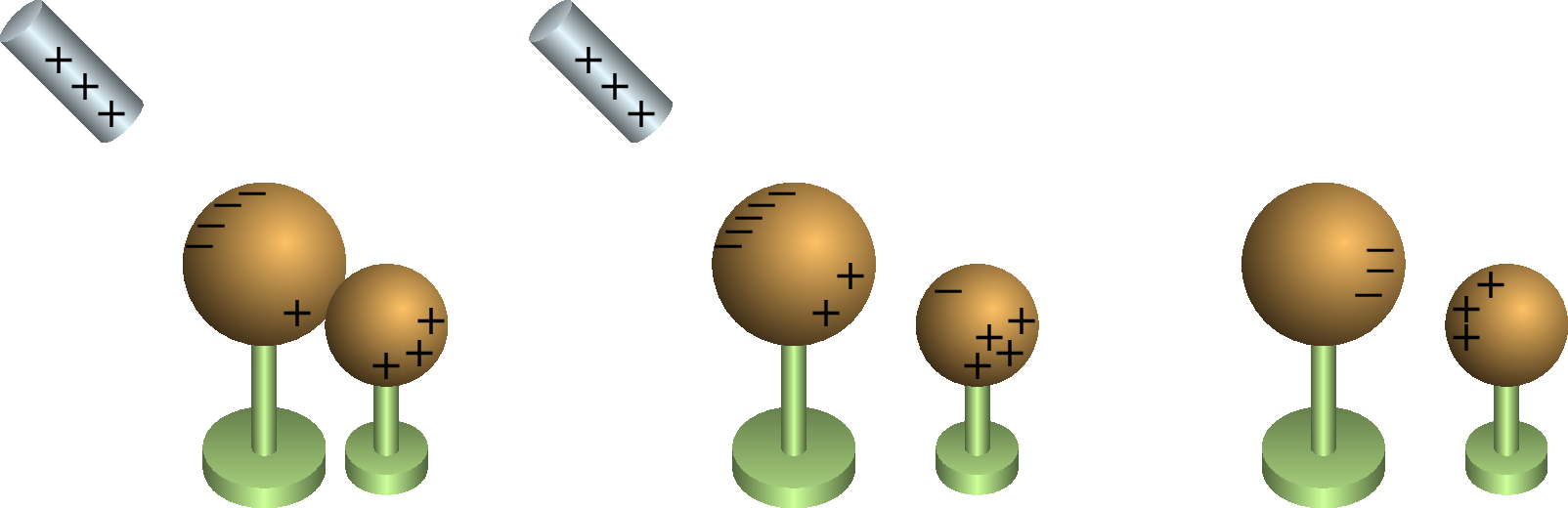
A eletrização por indução pode ser usada também para eletrizar dois objetos condutores, ficando ambos com cargas da mesma magnitude mas de sinais opostos. A figura 1.7 mostra o procedimento. Colocam-se os dois condutores a serem eletrizados em contacto e aproxima-se deles um objeto externo eletrizado; neste caso aproximou-se uma barra com carga positiva de um sistema de duas esferas condutoras neutras em contacto. São induzidas cargas positivas e negativas nas duas esferas; a esfera mais próxima da barra fica com carga negativa e a esfera mais distante com carga positiva.
Antes de afastar a barra eletrizada, separam-se as duas esferas, para que quando a barra seja afastada as cargas nas esferas não sejam recombinadas ficando neutras. Finalmente afasta-se a barra, ficando as duas esferas com cargas da mesma magnitude mas de sinais opostos.
Os condutores são mais facilmente eletrizáveis por indução do que os isoladores. O movimento dos eletrões de condução nos condutores permite uma relativamente fácil redistribuição de carga elétrica por indução e respetiva eletrização face aos isoladores, os quais não possuem cargas de condução.
1.4 Lei de Coulomb
Entre as experiências de eletrostática realizadas por Franklin, conta-se uma na qual introduziu pequenas bolinhas de cortiça dentro de uma taça metálica que tinha sido previamente isolada da mesa onde se encontrava e carregada eletricamente. Franklin observou que as bolinhas de cortiça não sentem a ação da força elétrica dentro da taça, ao contrário do que acontece fora dela, onde há forças elétricas que atraem a cortiça para a taça.
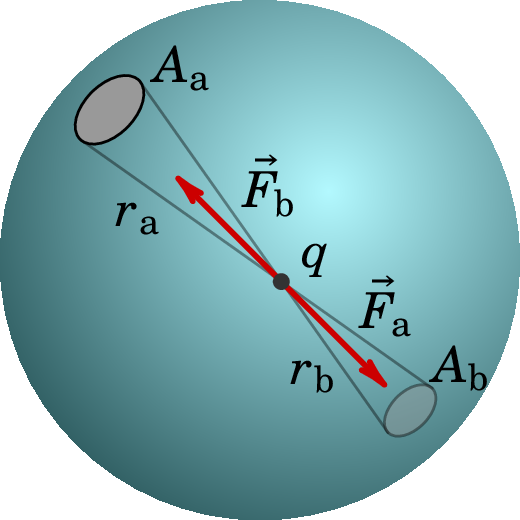
Priestley conseguiu explicar esse fenómeno da forma seguinte: considere-se uma esfera metálica carregada, como mostra a figura 1.8, e uma partícula com carga colocada num ponto qualquer dentro da esfera. Um conjunto contínuo de retas que passam pela partícula interseta a esfera, nos dois lados opostos à partícula, formando duas regiões com áreas e , que são diretamente proporcionais aos quadrados das distâncias e desde P até aos dois lados da esfera.
| (1.2) |
A mobilidade das cargas no metal e as forças repulsivas entre cargas do mesmo sinal, faz com que as cargas se distribuam uniformemente na superfície. Como tal, os valores absolutos das cargas nas duas regiões opostas da esfera, e , são diretamente proporcionais às áreas das duas regiões e a equação anterior implica:
| (1.3) |
As duas regiões nos lados opostos de produzem sobre a partícula duas forças opostas e . Se o módulo da força elétrica produzida por cada região é proporcional ao valor absoluto da carga na região, dividida pelo quadrado da distância até à partícula, então essas duas forças têm o mesmo módulo e anulam-se.
Qualquer outra região na superfície da esfera tem sempre uma respetiva região no lado oposto da carga e a força resultante dessas duas regiões sobre a carga também é nula. Conclui-se então que a força elétrica nula em qualquer ponto do interior da esfera condutora é consequência de que a força elétrica produzida por uma partícula com carga , sobre outra partícula com carga , é diretamente proporcional a e inversamente proporcional ao quadrado da distância entre as cargas. A lei de ação e reação também implica que o módulo da força elétrica de sobre seja o mesmo, ou seja, a força elétrica entre as partículas deverá ser também proporcional a . Resumindo, a expressão do módulo da força entre duas partículas com cargas e é
| (1.4) |
onde é a distância entre as cargas e é uma constante, chamada constante de Coulomb; a medição experimental dessa constante dá o valor
| (1.5) |
Nomeadamente, a força entre duas cargas elétricas de C, distanciadas de m, é igual a N. A constante de Coulomb também costuma ser escrita como onde
| (1.6) |
é a permitividade elétrica do vácuo (ver apêndice C).
A equação (1.4) é a lei de Coulomb:
A força elétrica entre duas cargas pontuais é diretamente proporcional ao produto das cargas e inversamente proporcional ao quadrado da distância entre elas.
A Lei de Coulomb (1.4) pode ser expressa à custa do uso dos vetores posição das cargas. O vetor posição de um ponto, em particular o de uma carga pontual, é o vetor que liga a origem do sistema de coordenadas escolhido ao ponto onde está a carga (ver figura 1.9). A força elétrica que uma carga pontual sente devido a outra carga pontual é então dada por:
| (1.7) |
onde é o módulo do vetor , que é o vetor posição de em relação a . O versor é um vetor com a direção e o sentido de mas com módulo igual a 1. O vetor posição relativa e o respetivo versor obtêm-se a partir dos vetores posição das duas cargas:
| (1.8) |
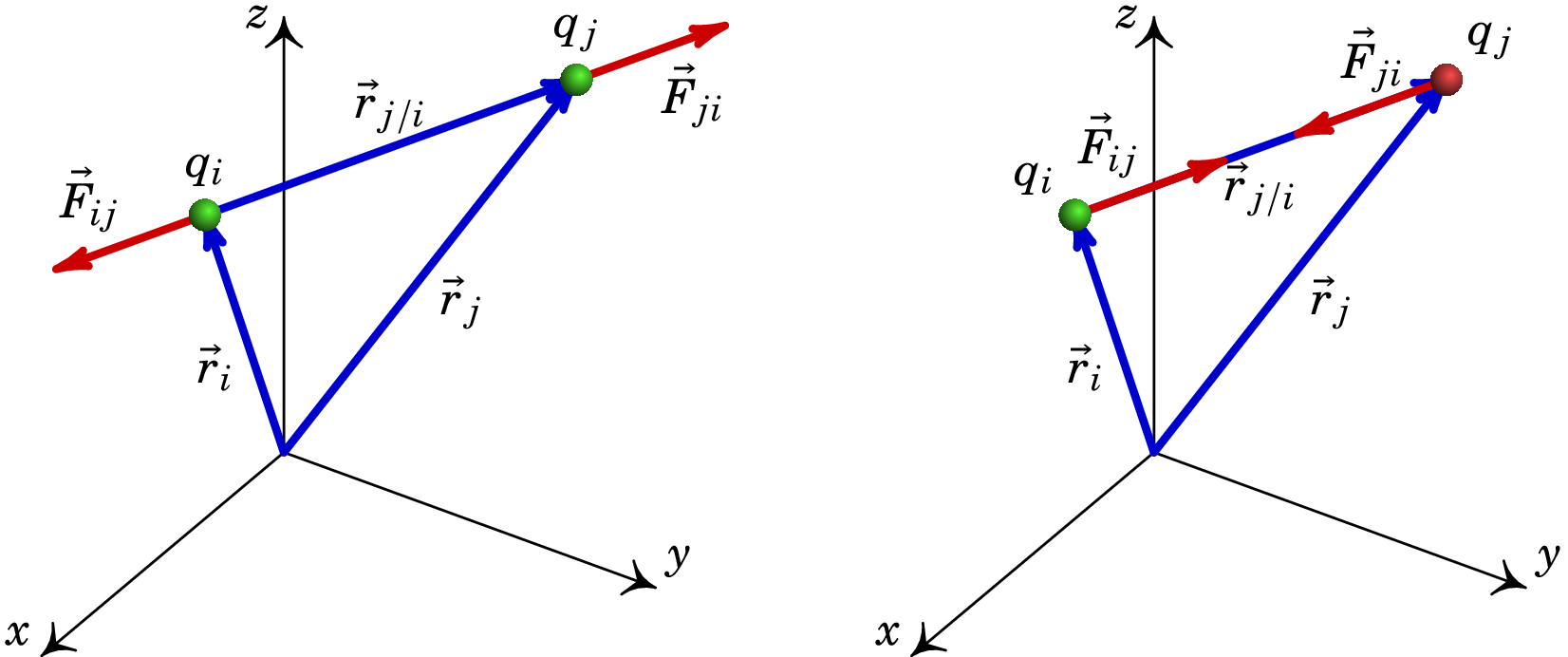
A lei de ação e reação implica que a força que exerce sobre é igual e oposta à força que exerce sobre . Efetivamente, na equação (1.7) a troca dos índices e só troca o sentido do versor ; como tal, , mas os módulos dessas duas forças são iguais: .
Na equação (1.7), a força tem a mesma direção do versor , i.e., a da linha que passa pelas duas cargas pontuais. O produto terá sinal positivo se as cargas tiverem o mesmo sinal, ou negativo se tiverem sinais opostos. Como tal, se o sinal das duas cargas for o mesmo, estará no mesmo sentido do versor e no sentido oposto: força repulsiva, como no lado esquerdo da figura 1.9. Já se os sinais das cargas forem opostos, o sentido de será oposto a e será no mesmo sentido de : força atrativa, como no lado direito da figura 1.9. Em qualquer caso os módulos das forças são diretamente proporcionais aos valores absolutos das cargas e inversamente proporcionais ao quadrado da distância entre elas.
As forças elétricas verificam o Princípio da Sobreposição: num sistema constituído por cargas pontuais (, …, ), a força elétrica resultante sobre uma dessas cargas, , é igual à soma vetorial das forças que todas as outras cargas exerceriam se interagissem isoladamente com . A expressão para a força elétrica resultante na carga é então,
A equação vetorial (1.7) é particularmente útil em três dimensões. Em duas dimensões é geralmente mais fácil usar a equação (1.4) para o módulo da força e desenhar a sua direção e sentido num diagrama que permita aplicar relações geométricas, tal como no exemplo dado a seguir.
A Lei de Coulomb é válida unicamente para cargas pontuais, ou seja, cargas concentradas em regiões muito pequenas do espaço. Para calcular as forças elétricas entre corpos com cargas distribuídas em regiões extensas é necessário dividir cada uma dessas regiões em várias regiões pequenas que possam ser aproximadas por cargas pontuais e obter as forças entre todas essas cargas pontuais a partir da equação (1.9).
Exemplo 1.1
Três partículas com cargas de , e encontram-se nos vértices de um triângulo equilátero de de lado. Determine a força total sobre a partícula de carga negativa.
Resolução. O primeiro que convém fazer é calcular o valor da constante eletrostática nas unidades relevantes no problema:
isto implica que, usando unidades de nC para as cargas, mm para as distâncias e o valor de para a constante , as forças calculadas pela Lei de Coulomb serão dadas em mN.
A seguir escolhe-se um sistema de eixos coordenados como mostra a figura seguinte.
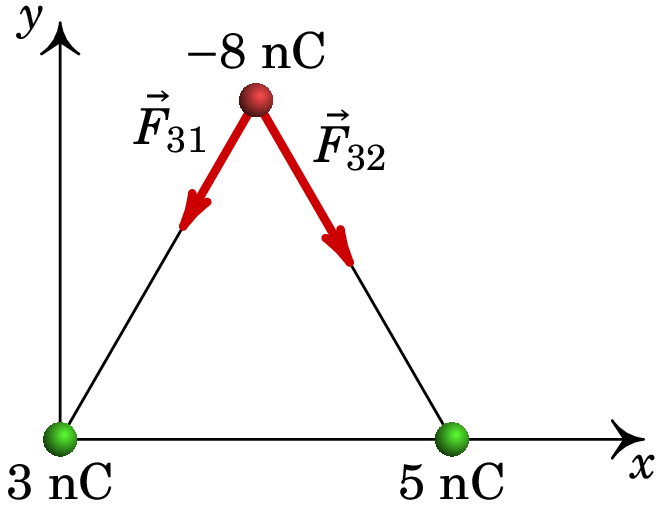
Sobre a partícula de carga nC atuam duas forças elétricas, produzidas pelas cargas de nC e nC. Os módulos dessas duas forças são
As duas forças são atractivas e fazem um ângulo de com a vertical. Como tal, as componentes da força resultante são
e o módulo da força resultante é
1.5 Campo elétrico
No exemplo 1.1, se a carga de nC fosse substituída, por exemplo, por nC é fácil ver que a força resultante nessa partícula ficava com o mesmo módulo mas em sentido oposto. E se a carga fosse nC em vez de nC, a força ficava no mesmo sentido mas com módulo igual a metade. Em geral, quaisquer que sejam as cargas que produzem forças sobre uma partícula com carga , colocada num dado ponto P do espaço, a força elétrica produzida sobre essa partícula é sempre diretamente proporcional ao valor da carga , i.e.,
| (1.10) |
onde o vetor chama-se campo elétrico. No sistema internacional de unidades, as unidades do campo elétrico são então N/C. De referir que a expressão (1.10) 22Comparar a expressão (1.10) com a força gravítica: uma massa colocada num campo gravítico sofre uma força gravítica dada por . Junto da superfície da Terra, o campo gravítico é aproximadamente constante e igual à aceleração gravítica . é geral, i.e., é válida para qualquer campo elétrico quer seja devido a uma qualquer distribuição de carga elétrica quer seja devido a indução eletromagnética, assunto este que será abordado no Capítulo 9.
Neste capítulo estamos interessados principalmente na força elétrica (1.10) que atua sobre uma carga pontual numa região onde existe campo elétrico conhecido . Força essa que não terá de ter a forma da lei de Coulomb (1.7), a menos que o campo em questão seja produzido por outra carga pontual. O problema de como encontrar a expressão do campo elétrico devido a um sistema de cargas será adiado para o capítulo 2. Neste capítulo vamos mostrar apenas a expressão do campo elétrico produzido por uma única carga pontual e um método gráfico de visualizar o campo de várias cargas pontuais.
Para determinar o campo elétrico produzido por uma carga pontual , num ponto P qualquer, calcularemos a força elétrica que esta produziria sobre uma outra carga pontual colocada nesse ponto. Escolhendo a origem no ponto onde está a carga , a distância entre as duas cargas será o módulo do vetor posição do ponto P onde se encontra a carga (figura 1.10). De acordo com a lei de Coulomb (1.7), a força elétrica de sobre é,
| (1.11) |
onde é o versor radial em coordenadas esféricas (secção A.2.4 do apêndice A), i.e., um vetor unitário que aponta na direção e sentido do vetor posição do ponto P (figura 1.10).
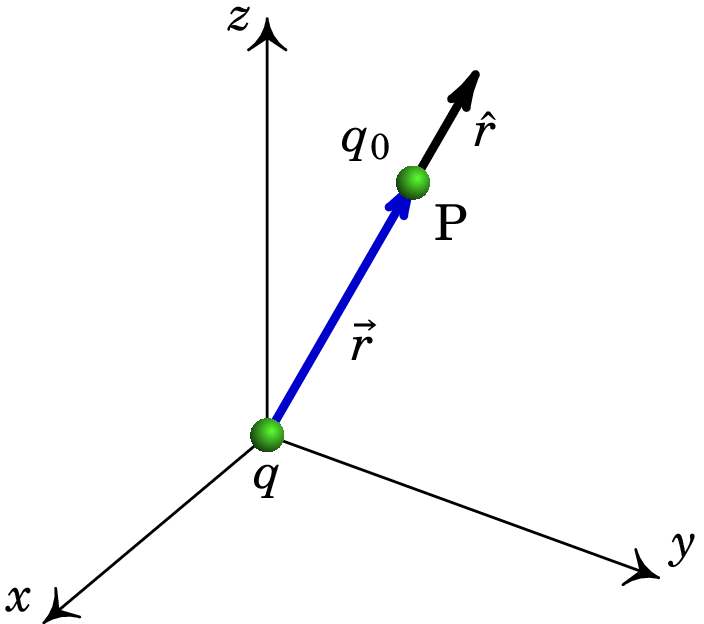
O campo elétrico no ponto de vetor posição , produzido pela carga na origem, obtém-se dividindo a expressão (1.11) pela carga :
| (1.12) |
Conclui-se que a intensidade do campo elétrico de uma carga pontual num ponto é diretamente proporcional ao valor absoluto da carga e inversamente proporcional ao quadrado da distância entre a carga e o ponto. Em coordenadas esféricas, o campo de uma carga pontual situada na origem possui apenas componente radial esférica e esta apenas depende da coordenada radial esférica , i.e., , onde . A figura 1.11 mostra o gráfico dessa função; o valor negativo, quando a carga é negativa, indica que o vetor aponta no sentido oposto do versor radial .
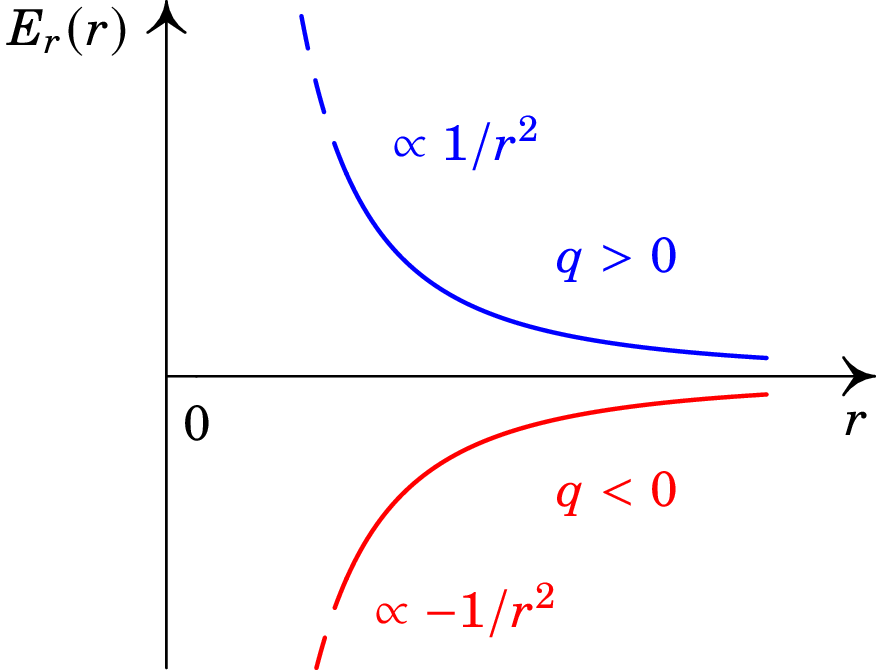
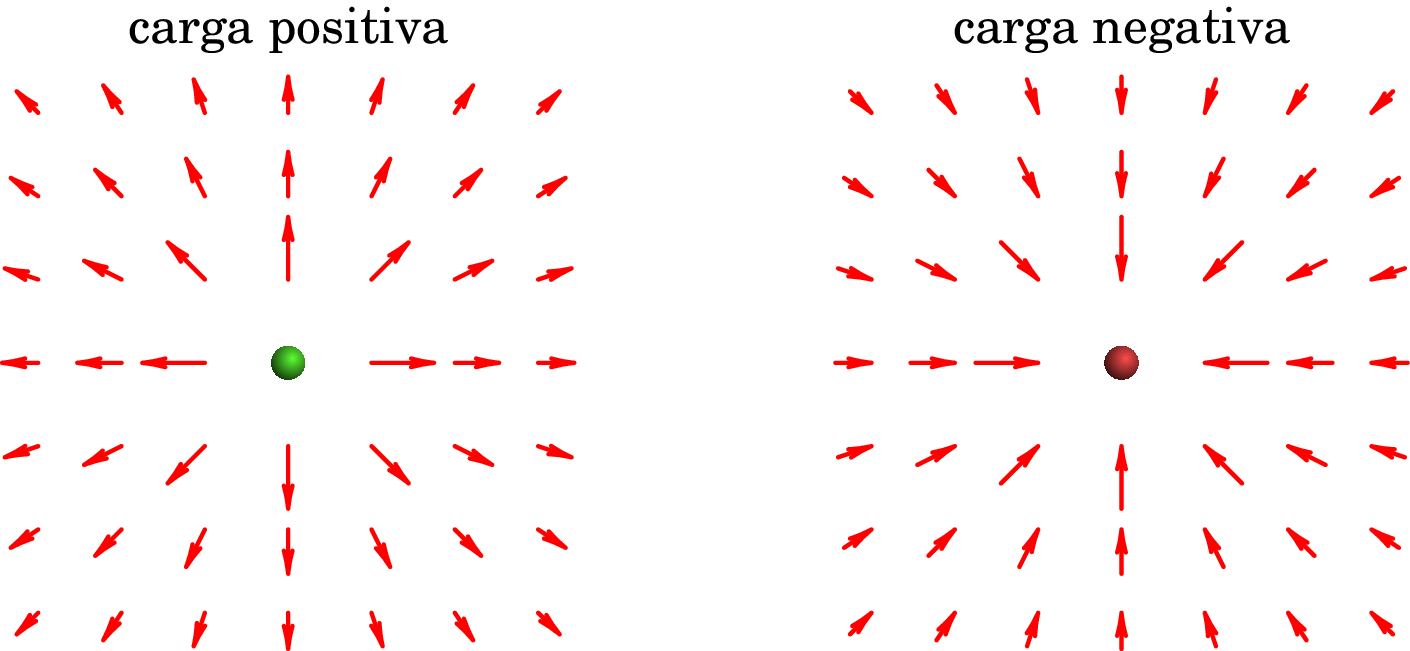
O campo elétrico é um campo vetorial, i.e., em cada ponto do espaço existe um vetor, denominado por vetor campo elétrico , vetores estes que são uma representação do campo elétrico (ver figura 1.12). O campo vetorial que representa o campo elétrico é divergente da carga se a carga for positiva ou convergente na carga se a carga for negativa, tal como mostra a figura 1.12. Os vetores que representam o campo elétrico existem no espaço tridimensional. Contudo, para sistemas de carga onde existe simetria em relação a um eixo (i.e., o sistema é invariante sob uma rotação de um ângulo qualquer em torno desse eixo) é suficiente representar os vetores campo elétrico num plano contendo o eixo de simetria (ver figura 1.12).
Na tabela 1.2 são apresentados valores típicos da intensidade do campo elétrico em várias situações.
| Situação | (N/C) |
| Atmosfera num dia normal | |
| Atmosfera em dia de trovoada | |
| Carga pontual de nC | |
| à distância de cm | |
| Raio numa trovoada | |
| Protão à distância do raio do átomo | |
| de hidrogénio |
Combinando as equações (1.10) e (1.12) obtém-se a Lei de Coulomb (equação (1.7)) para a força elétrica entre duas cargas pontuais — verifique.
Vimos que uma carga pontual, independentemente de existirem ou não outras cargas, produz por si só um campo elétrico em todos os pontos do espaço à sua volta. Deste modo, o campo elétrico está diretamente associado a uma partícula, neste caso uma carga pontual, e não a um par de partículas como é o caso da Lei de Coulomb.
A interpretação física do campo elétrico é que uma carga elétrica altera o espaço à sua volta (ver figura 1.13) e essa alteração é o campo elétrico. Essa alteração do espaço pode ser detetada através da força que outras partículas com carga sentem quando colocadas nesse campo elétrico. Assim, a interação entre duas cargas não ocorre diretamente entre elas à distância, mas sim é mediada por um campo, a saber, o campo elétrico.

O conceito de campo elétrico foi adotado pelos físicos do século xix, para explicar como as forças eletrostáticas e gravitacionais podem atuar à distância, entre duas partículas que não estão em contacto. O campo era associado a um meio invisível e imaterial chamado éter; o campo seria como uma onda que se propaga no éter produzindo forças em outros corpos.
A teoria do éter foi abolida na física do século xx, mas o conceito do campo como alteração do espaço prevalece. Existe evidência experimental de que a ação de uma partícula sobre outra não ocorre instantaneamente, mas propaga-se desde uma partícula até outra à velocidade da luz. Se, por exemplo, neste instante uma grande quantidade de carga negativa saísse do Sol, ficando este com carga total positiva, as forças produzidas por essas cargas só seriam detetadas na Terra minutos mais tarde, o tempo que o campo demora a deslocar-se do Sol até à Terra, à velocidade da luz.
Exemplo 1.2
Um protão passa pela origem, em , com velocidade Mm/s, dentro de uma região onde há vácuo e campo elétrico uniforme, . Determine o valor que deverá ter para que o protão atravesse o eixo dos em cm.
Resolução. A força elétrica sobre o protão será constante, igual a:
O peso do protão pode ser ignorado, porque com velocidade da ordem de Mm/s e distância da ordem de 10 cm, espera-se um tempo da ordem de segundos e durante esse tempo o efeito da aceleração da gravidade é desprezável. Como tal, a aceleração do protão será:
onde kg é a massa do protão (ver apêndice C). Essa aceleração constante implica movimento parabólico, tal como um projétil. A componente da velocidade permanece constante, igual a 3 Mm/s e o tempo que o protão demora até atravessar o eixo dos , em cm é:
A trajetória parabólica, com eixo paralelo ao eixo dos , implica que quando o protão atravessar novamente o eixo dos terá componente da velocidade com o mesmo valor absoluto do seu valor inicial , mas com sinal negativo, ou seja, Mm/s. Usando a relação entre a projeção da velocidade e a componente da aceleração,
obtém-se o valor de :
O resultado negativo indica que o campo deverá apontar no sentido negativo do eixo do .
1.6 Linhas de campo elétrico
O campo elétrico pode ser representado por vetores que indicam a intensidade, a direção e o sentido do vetor em vários pontos do espaço, tal como na figura 1.12. Outra forma mais simples de representar o campo é por meio de linhas que seguem a direção do campo com uma seta a indicar o seu sentido; em cada ponto de uma dessas linhas de campo, o campo é o vetor tangente no sentido indicado pela seta (figura 1.14).
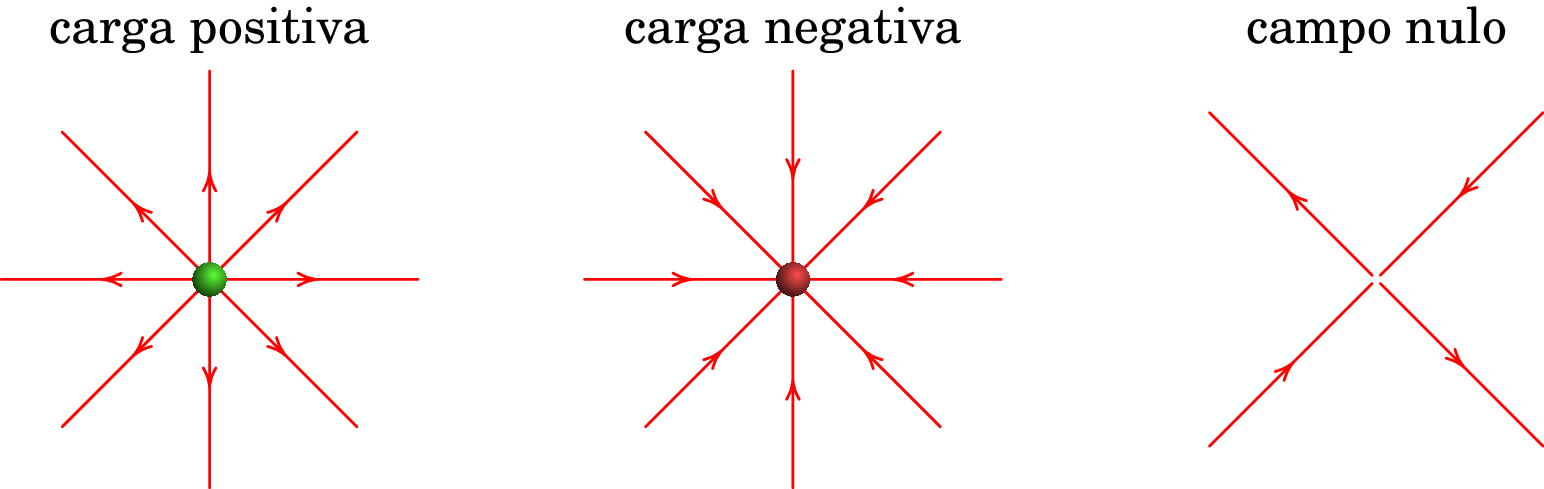
As linhas de campo elétrico têm as seguintes propriedades importantes:
-
•
Na vizinhança de uma carga pontual positiva as linhas de campo divergem em todas as direções e na vizinhança de uma carga negativa as linhas de campo convergem de todas as direções (ver figura 1.14). As linhas de campo também podem começar ou terminar no infinito.
-
•
Duas linhas de campo nunca se cruzam; num ponto de cruzamento o campo teria duas direções diferentes, o que não é possível.
-
•
Num ponto onde há linhas de campo que se aproximam dele e linhas que se afastam do ponto, o campo elétrico é necessariamente nulo, (o campo não pode ter nenhuma direção).
As linhas de campo são linhas no espaço tridimensional. Tal como para a representação vetorial do campo elétrico, para sistemas de carga invariantes sob uma rotação de um ângulo qualquer em torno de um eixo de simetria, basta representar as linhas de campo num plano contendo esse eixo.
Exemplo 1.3
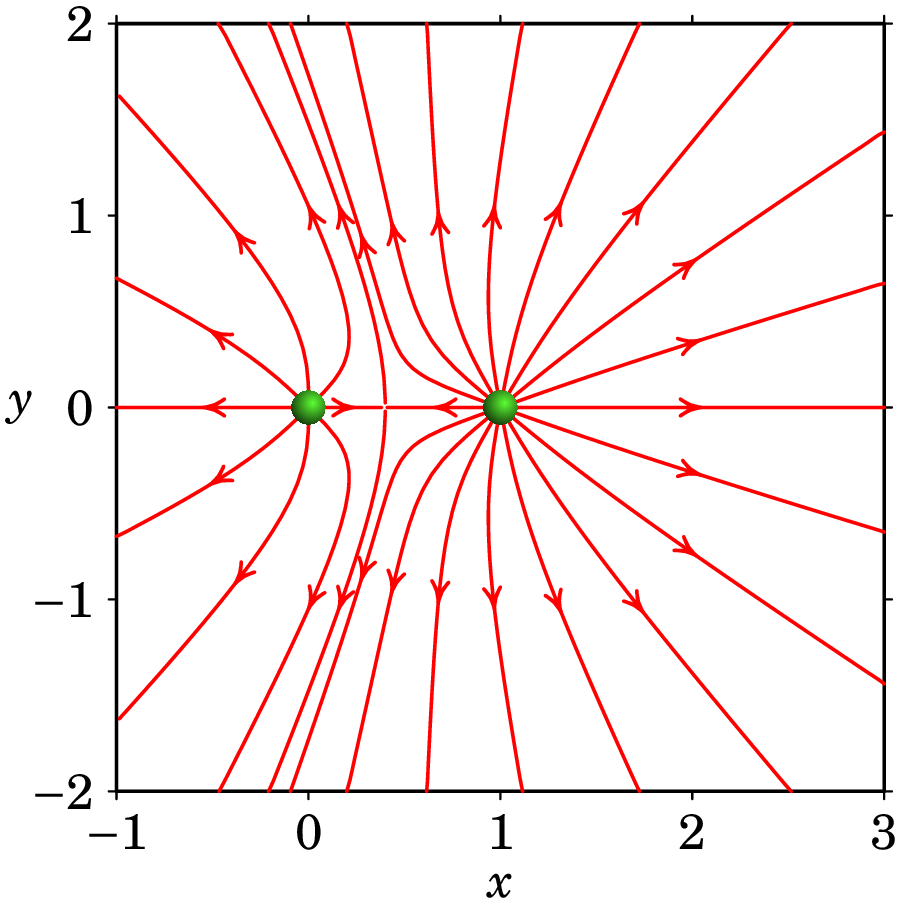
A figura mostra as linhas de campo de duas cargas pontuais, nos pontos e , e no ponto o campo é nulo. Determine os sinais das duas cargas e a relação entre elas.
Resolução. Como há linhas a sair em todas direções nos pontos e as duas cargas são positivas. No ponto onde o campo é nulo, os campos das duas cargas (carga da esquerda) e (carga da direita) anulam-se. Como tal, são vetores opostos e com o mesmo módulo:
Como as duas cargas são positivas a relação entre as cargas é igual à relação entre os seus valores absolutos, ou seja, a relação entre a carga da direita e a da esquerda é .
Em qualquer sistema de duas cargas pontuais cuja soma não seja zero, existe um ponto de campo nulo onde terminam e saem linhas de campo. Quando a relação entre os valores das cargas é uma relação simples de números inteiros, como no caso do exemplo 1.3, o desenho das linhas de campo pode fornecer mais informação, para além do sinal das cargas e eventualmente de pontos de campo nulo, se forem usadas as seguintes regras:
-
•
As linhas de campo que divergem de uma ou convergem numa carga pontual são representadas com separação angular uniforme e o número de linhas em cada carga é proporcional ao valor absoluto de cada carga.
-
•
Num ponto onde o campo elétrico é nulo o número de linhas convergentes neste ponto deve ser igual ao número de linhas divergentes do mesmo.
-
•
A grandes distâncias de um sistema de cargas pontuais, ocupando uma região finita do espaço, as linhas de campo comportam-se como se tivessem origem numa carga pontual com carga igual à carga total do sistema.
Se as linhas de campo forem assim representadas, a intensidade relativa do campo elétrico será mais forte onde a densidade de linhas (número de linhas por unidade de superfície perpendicular às linhas) for maior e mais fraco onde as linhas estiverem mais distanciadas.
No exemplo 1.3 foram usadas essas regras. Traçaram-se 8 linhas de campo a sair da carga da esquerda, distanciadas entre si, e 18 linhas a sair da carga da direita, distanciadas (a relação entre as cargas é ). No segmento que une as duas cargas, as direções opostas das linhas que saem de cada carga implica que deverá haver um ponto de campo nulo, onde essas linhas convergem. Deverá então haver outras duas linhas que divergem desse ponto. Confere-se que há um total de 26 linhas a afastarem-se até ao infinito, que correspondem à carga total, a qual é proporcional a 13. A grandes distâncias do sistema, i.e., para distâncias muito maiores do que a separação entre as cargas, as linhas de campo tenderiam a serem 26 linhas divergentes, radiais e igualmente espaçadas com entre si.
Para além das cargas pontuais, um sistema importante em eletromagnetismo é o dipolo elétrico. Um dipolo elétrico é constituído por duas cargas elétricas iguais em valor absoluto e de sinais contrários e distanciadas de (figura 1.15).
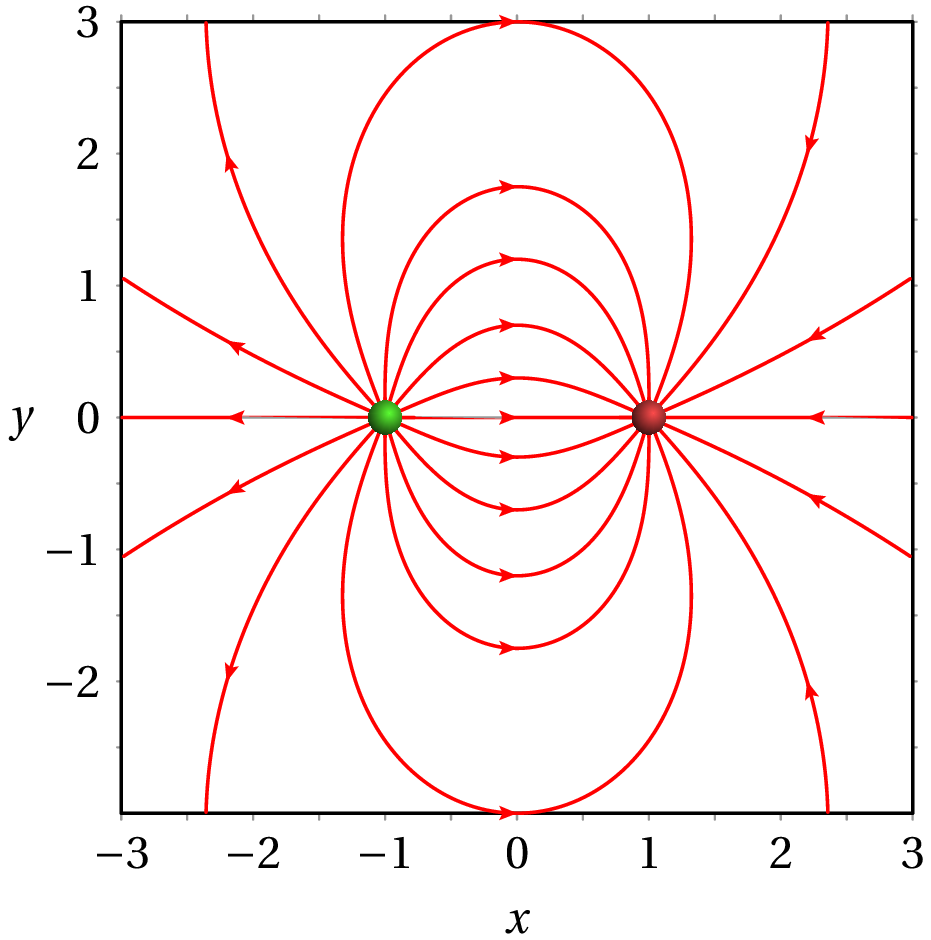
A figura 1.15 mostra as linhas de campo de um dipolo com unidades. Observe-se que, como as duas cargas têm o mesmo valor absoluto, o mesmo número de linhas de campo que divergem da carga positiva (em ) convergem na carga negativa (em ). As linhas que saem da figura no lado esquerdo, não se afastam até ao infinito, mas curvam-se, ligando às linhas de campo que entram no lado direito da figura. Qualquer linha de campo é uma curva que começa na carga positiva e termina na negativa; isso é uma consequência da carga total do sistema ser nula.
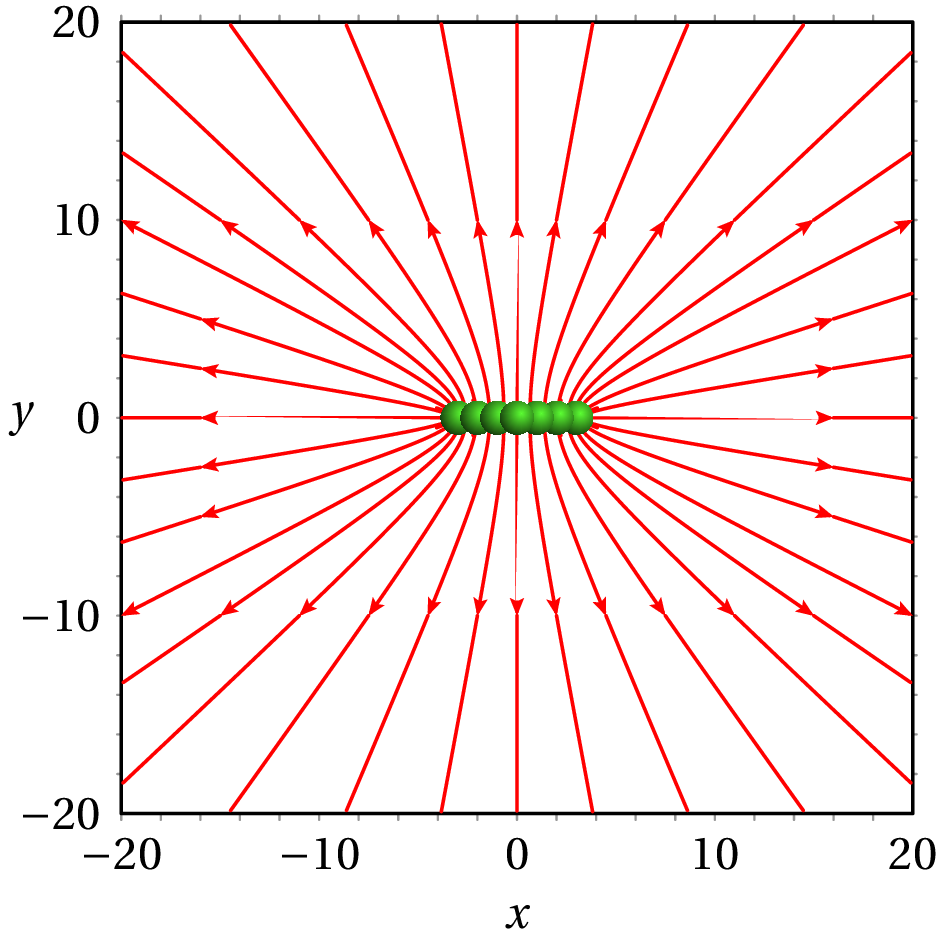
Uma distribuição contínua de cargas pode ser aproximada por um conjunto de cargas pontuais. Por exemplo, a figura 1.16 mostra as linhas de campo de uma carga distribuída uniformemente no segmento do eixo entre e , obtidas aproximadamente usando 7 cargas pontuais, iguais e equidistantes, entre e .
Na figura 1.16, observe-se que na vizinhança da origem as linhas de campo são aproximadamente paralelas. A figura 1.17 mostra a região próxima da origem, com , onde as linhas de campo apontam para cima e são aproximadamente paralelas. Linhas de campo paralelas indicam um campo uniforme, neste caso , que é um campo vetorial com direção, sentido e intensidade constantes em toda a região. As linhas costumam ser traçadas com separação constante, para indicar que a intensidade é a mesma em todos os pontos.
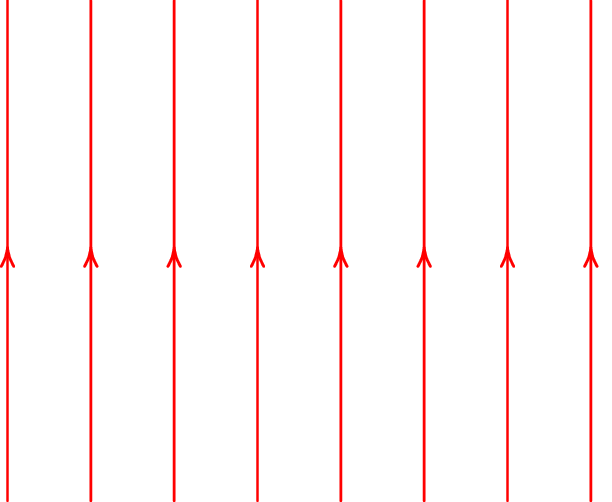
A aproximação do campo elétrico uniforme (figura 1.17) só pode ser válida numa região finita do espaço. Fora dessa região as linhas de campo elétrico deixam de ser paralelas, afastando-se umas da outras, já que a intensidade do campo elétrico aproxima-se de zero no infinito.
1.7 Campo elétrico em condutores e isoladores
Nas secções anteriores temos considerado uma situação idealizada em que existem algumas cargas isoladas no vácuo. Cada carga produz um campo elétrico que se propaga no vácuo e pode interagir com outras cargas produzindo forças sobre elas.
Na prática, o vácuo não existe e as cargas isoladas estarão sempre inseridas dentro de algum meio material. O campo elétrico produzido pelas cargas isoladas atua nos átomos desse meio, dando origem a um campo induzido que se sobrepõe ao campo dessas cargas. Na prática, o campo elétrico que observamos é essa sobreposição dos campos das cargas isoladas e o campo induzido no meio onde elas estão inseridas.
Se um condutor é colocado numa região onde existe campo elétrico, como a nuvem eletrónica de condução tem carga negativa, desloca-se no sentido oposto às linhas de campo. O deslocamento dos eletrões de condução faz surgir carga negativa num extremo (excesso de eletrões) e carga positiva no extremo oposto (falta de eletrões) — num sólido, os núcleos atómicos podem ser considerados fixos. Se a carga total do condutor é nula, o valor absoluto dessas cargas nos extremos será igual. Essas cargas de sinais opostos nos extremos opostos do condutor produzem um campo elétrico interno, no sentido oposto ao campo externo e quando as cargas acumuladas nos extremos sejam suficientemente elevadas, dentro do condutor os dois campos anulam-se e o movimento dos eletrões de condução cessa.
A figura 1.18 mostra uma barra com carga positiva, colocada na proximidade de uma esfera condutora montada num suporte isolador; a nuvem eletrónica de condução na esfera aproxima-se da barra, deixando carga positiva na região mais afastada da barra e a mesma quantidade de carga negativa na região mais próxima da barra. Se o suporte não fosse isolador, entravam no condutor eletrões do suporte e as cargas positivas indicadas na figura desapareciam.
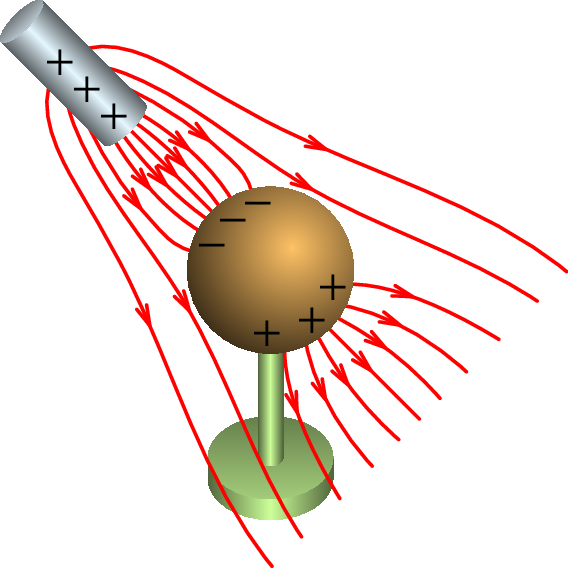
Se a barra tivesse carga negativa, em vez de positiva, as posições das cargas positivas e negativas na esfera seriam trocadas. Uma vez acumuladas cargas de sinais opostos nos extremos da esfera, o campo elétrico total dentro da esfera é nulo; como tal, as linhas de campo não penetram na esfera e os eletrões de condução dentro da esfera não sentem qualquer força elétrica. Nos dois casos (barra com carga positiva ou negativa), as cargas na superfície da esfera mais próxima da barra são atraídas para a barra e essa atração é maior do que a repulsão sobre as cargas na superfície mais afastada da barra. Assim, qualquer objeto externo com carga de qualquer sinal produz sempre uma força atrativa nos condutores com carga total nula.
Se a mesma experiência é realizada com uma esfera isoladora (figura 1.19), não há movimento de cargas de condução para a superfície e o campo dentro da esfera não se anula. Contudo, há movimentação das cargas dentro de cada molécula do material, ficando polarizadas, i.e., a nuvem eletrónica de cada molécula desloca-se dentro do seu interior no sentido oposto do campo. Cada molécula é um dipolo microscópico com o seu momento dipolar (vetor que aponta da carga negativa para a positiva; ver problema 11) orientado na direção do campo. A figura mostra alguns dipolos macroscópicos para dar uma ideia da orientação dos dipolos microscópicos.
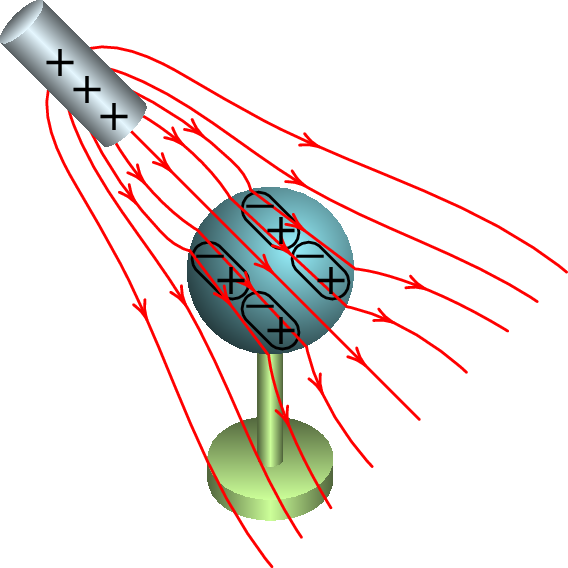
O campo da barra é deformado pela polarização do dielétrico, problema esse que será abordado no capítulo 4. Para já, o que interessa saber é que como resultado da polarização do dielétrico existirão cargas de polarização de sinal oposto ao da carga da barra na parte da superfície da esfera mais próxima da barra e cargas do mesmo sinal na parte da superfície mais afastada da barra. Como consequência, a barra exerce força atrativa sob a esfera, qualquer que seja o sinal da carga na barra. Um objeto eletrizado produz sempre força atrativa sob outros objetos isoladores eletricamente neutros.
Problemas
-
1.1.
A unidade SI de carga elétrica é o coulomb (C). Mesmo para objetos do dia a dia, 1 C é uma carga elétrica enorme.
(a) Duas cargas, consideradas pontuais, de C cada estão à distância de cm. Calcule a força elétrica entre elas. Compare e comente o valor obtido com o peso de um Boeing , considerando a sua massa como sendo de toneladas.
(b) Considere duas cargas elétricas iguais à distância de cm. Calcule o valor de de modo a que força entre as cargas seja de N. Comente o valor obtido. -
1.2.
Uma esfera de cobre possui um volume de dm e encontra-se eletricamente neutra. Dados do cobre: densidade volúmica de massa g.cm, número atómico , massa atómica .
(a) Calcule o número de eletrões existentes na esfera, bem como a sua carga.
(b) Caso o número de eletrões sofra uma variação de %, determine a carga elétrica que a esfera adquire.
(c) Considerando agora uma segunda esfera idêntica à inicial, altera-se em cada uma o seu número de eletrões de %. Calcule a força elétrica entre as esferas a uma distância de cm. Determine a massa duma esfera com peso igual a essa força e compare-a com a massa da Terra ( kg).
(d) Calcule o número de eletrões a serem removidos (injetados) de modo à esfera inicial ficar eletrizada positivamente (negativamente) com carga C (-C). Compare com o número total de eletrões inicial.
(e) Comente os resultados anteriores. -
1.3.
Determine a força elétrica resultante sobre cada uma das cargas representadas na figura.
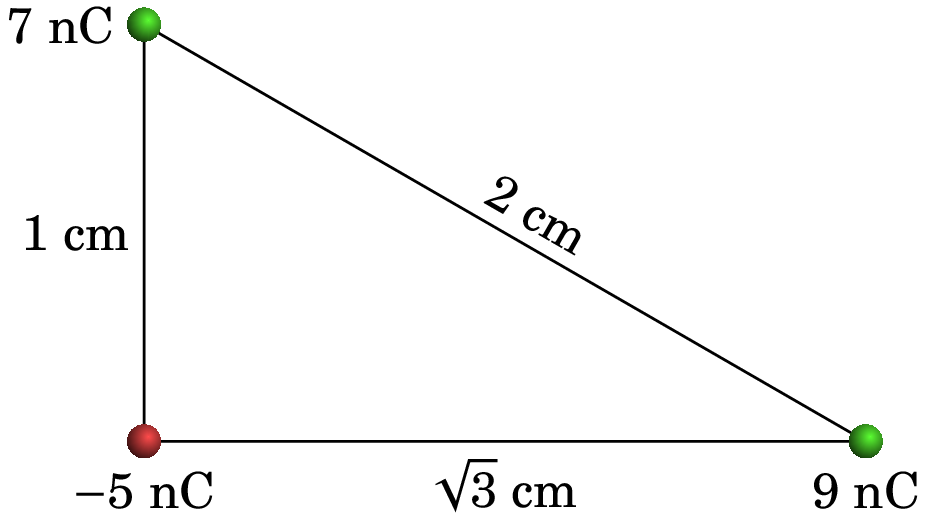
-
1.4.
Três cargas pontuais estão ligadas por dois fios isoladores de cm cada (ver figura). Calcule a tensão em cada fio.

-
1.5.
A soma dos valores de duas cargas pontuais e é C. Quando estão afastadas 3 m entre si, o módulo da força exercida por cada uma delas sobre a outra é 24 mN. Determine os valores de e , se: (a) Ambas cargas são positivas. (b) Uma das cargas é positiva e a outra negativa.
-
1.6.
Duas pequenas esferas condutoras, com cargas nC e nC, e com a mesma massa , são coladas a dois fios isoladores, cada um com 8 cm de comprimento. Os fios são então colados numa barra horizontal, em dois pontos a uma distância cm entre si. A repulsão eletrostática entre as cargas faz com que os dois fios se inclinem um ângulo em relação à vertical. Determine o valor da massa .
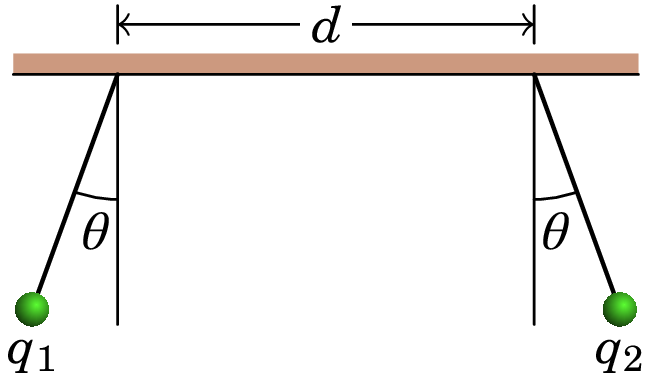
-
1.7.
Quatro cargas pontuais , , e encontram-se nos vértices de um tetraedro regular de aresta . Determine o módulo da força resultante sobre a carga .
-
1.8.
Um eletrão desloca-se no sentido positivo do eixo dos sob a ação de um campo elétrico. A expressão da sua velocidade é , onde a coordenada é dada em metros e a velocidade em m/s. Determine a expressão do campo elétrico , ao longo do eixo dos , em N/C (a massa de um eletrão é kg - ver apêndice C).
-
1.9.
No interior do Sol dão-se reacções de fusão nuclear que libertam a energia responsável pela sua luminosidade. A reacção mais importante é chamada cadeia pp-I e consiste na série seguinte de reações nucleares:
onde p é um protão, d é um núcleo de deutério, um positrão, um neutrino e um fotão. e são núcleos de hélio com 3 e 4 nucleões33O protão e o neutrão são designados por nucleões, por serem constituintes do núcleo atómico., respetivamente. Usando o princípio da conservação da carga determine:
-
(a)
A carga do núcleo de deutério, sabendo que a carga do positrão é a mesma do protão e que o neutrino não tem carga.
-
(b)
A carga dos núcleos de e , sabendo que um fotão não tem carga.
-
(c)
O número de neutrões nos núcleos de e .
-
(a)
-
1.10.
O átomo de Hidrogénio possui um protão e um eletrão, os quais segundo o modelo de Bohr se encontram à distância de um raio de Bohr (ver apêndice C). Calcule e compare as forças elétrica e gravítica entre o protão e o eletrão. Comente o resultado.
-
1.11.
Uma carga elétrica divide-se em duas cargas e . As duas cargas são colocadas a uma distância . Quais devem ser os seus valores de modo à força elétrica ser máxima?
-
1.12.
Duas cargas pontuais de carga e situadas no eixo nos pontos e , respetivamente. Exceptuando o infinito, determine o(s) ponto(s) onde o campo elétrico é nulo e desenhe as linhas de campo para os seguintes casos:
(a) C e C.
(b) C e C.
(c) nC e nC.
(d) nC e nC.
(e) Em geral, para valores arbitrários de e , onde estarão o(s) ponto(s) onde o campo elétrico é nulo? -
1.13.
Considere duas cargas pontuais nC e nC localizadas nos pontos de coordenadas cartesianas e , respectivamente. Calcule a força exercida em por .
-
1.14.
Um corpo tem duas cargas concentradas em dois pontos distanciados de , constituindo assim um dipolo elétrico. O corpo é colocado dentro de um campo elétrico externo uniforme, , tal como mostra a figura. O vetor , designado momento dipolar, tem módulo e aponta na direção e sentido da carga negativa para a carga positiva.
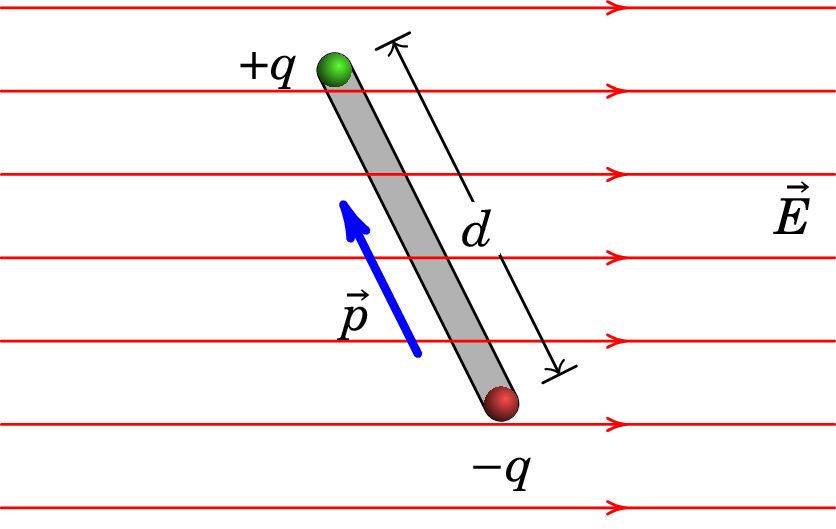
(a) Qual a força elétrica total que atua no dipolo? Interprete fisicamente o resultado.
(b) Mostre que no dipolo atua um binário dado por . Interprete fisicamente o resultado. -
1.15.
Duas cargas e positivas encontram-se fixas no eixo dos em e . Uma terceira partícula de massa e carga negativa apenas se pode mover livremente no eixo .
(a) Calcule o vetor força elétrica na carga , para qualquer valor da posição da carga .
(b) Que condição se deve verificar para que a força elétrica tenha apenas componente segundo ? -
1.16.
Considere a região do espaço , na qual existe um campo elétrico uniforme dado por , onde é uma constante positiva. Uma partícula de massa e carga elétrica é colocada neste campo no ponto com uma velocidade inicial . Admita que a aceleração da gravidade é desprezável.
(a) Determine a aceleração, a velocidade e a posição da partícula em função do tempo.
(b) Determine e desenhe a sua trajetória para os casos e . -
1.17.
A figura mostra as linhas de campo elétrico de um sistema de duas cargas pontuais, no eixo dos , na origem e em . Sabendo que a carga na origem é igual a 2.7 nC:
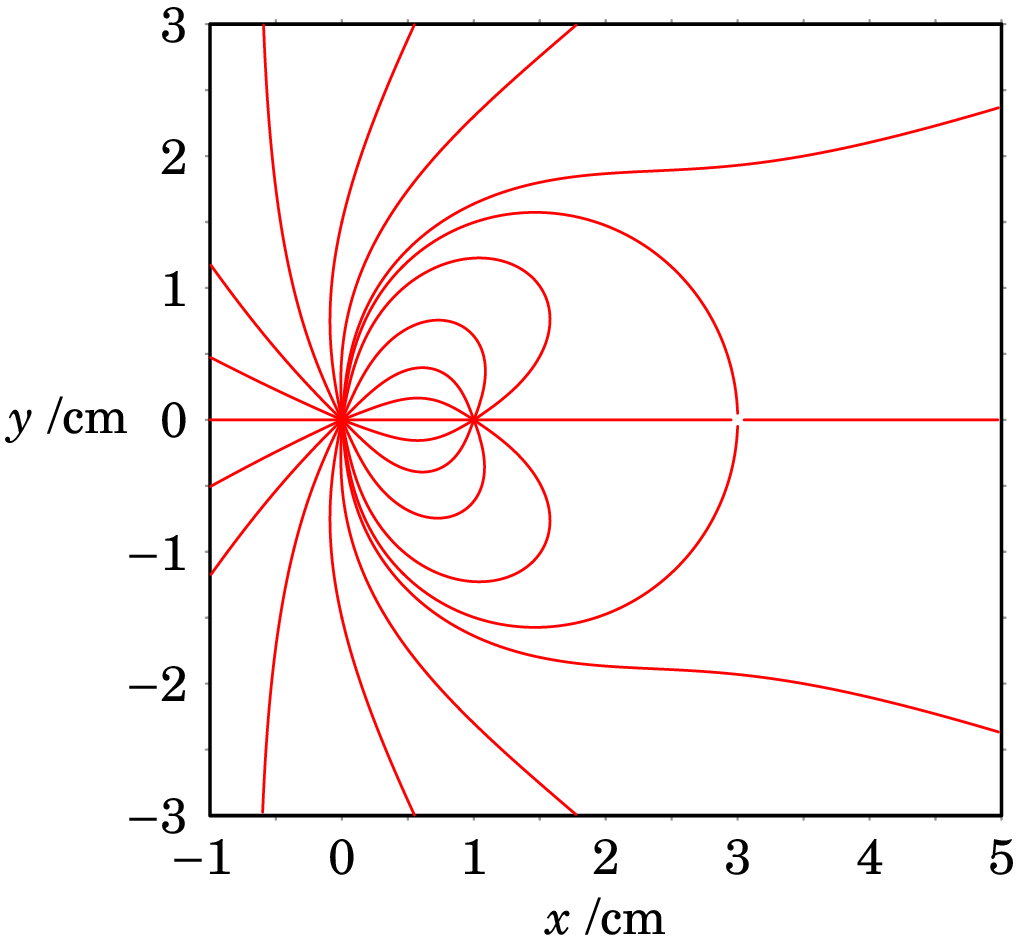
(a) Coloque uma seta em cada linha de campo indicando o seu sentido.
(b) Determine o valor da carga em .
(c) Calcule a força entre as duas cargas. -
1.18.
Considere uma região do espaço onde existe um campo elétrico uniforme , onde é uma constante positiva. Uma partícula de massa e carga é lançada nessa região com velocidade , sendo o ponto de lançamento a origem. Assuma que a aceleração da gravidade é desprezável.
(a) Calcule a velocidade e a posição da partícula em função do tempo e descreva o seu movimento para os casos e .
(b) Determine as coordenadas do ponto de impacto num alvo colocado perpendicular ao eixo dos e a uma distância do ponto de partida. -
1.19.
O campo elétrico na atmosfera terrestre tem intensidade de aproximadamente 150 N/C e aponta na direção e sentido do centro da Terra. Calcule a razão entre o peso de um eletrão e o módulo da força elétrica oposta exercida pelo campo elétrico da atmosfera (a massa do eletrão é kg e admita que a aceleração da gravidade é m/s — ver apêndice C).
-
1.20.
Um sistema de três cargas pontuais está em equilíbrio (a força eletrostática sobre cada carga é zero). Sabendo que duas das cargas são e , separadas por uma distância , calcule o valor e a posição da terceira carga.
-
1.21.
Um núcleo de hélio (também chamado partícula alfa) é formado por dois protões e dois neutrões. A força eletrostática entre os protões é repulsiva e muito forte, pois a distância entre eles é muito pequena (aproximadamente m). A estabilidade do núcleo é devida à existência de uma outra força entre protões e neutrões, chamada força forte. Para ter uma ideia da ordem de grandeza da força forte, calcule a força eletrostática entre os dois protões no núcleo de hélio e, usando a segunda lei de Newton, a aceleração que esta produziria num protão.
Respostas
-
1.1.
(a) Força elétrica N, peso do avião N. A força elétrica é o peso de aproximadamente meio milhão de aviões.
(b) C. -
1.2.
(a) e C. (b) C.
(c) Força elétrica N. Massa N, que é aproximadamente 11 % da massa da Terra.
(d) eletrões, % do número inicial de eletrões.
(e) Ver discussão no livro de problemas resolvidos. -
1.3.
Com origem na carga nC, eixo dos na direção de nC, e eixo dos na direção de nC, as forças são:
mN mN
mN -
1.4.
A tensão no fio do lado esquerdo é 285 N e no fio do lado direito 559 N.
-
1.5.
(a) 5.98 µC, e 4.02 µC (b) 12.0 µC, e µC.
-
1.6.
g.
-
1.7.
µN.
-
1.8.
N/C.
-
1.9.
(a) . (b) para ambos. (c) possui 1 neutrão e possui 2 neutrões.
-
1.10.
N, N, . A intensidade da interação elétrica é muitíssimo maior do que a da interação gravítica.
-
1.11.
.
-
1.12.
(a) O campo é nulo em .
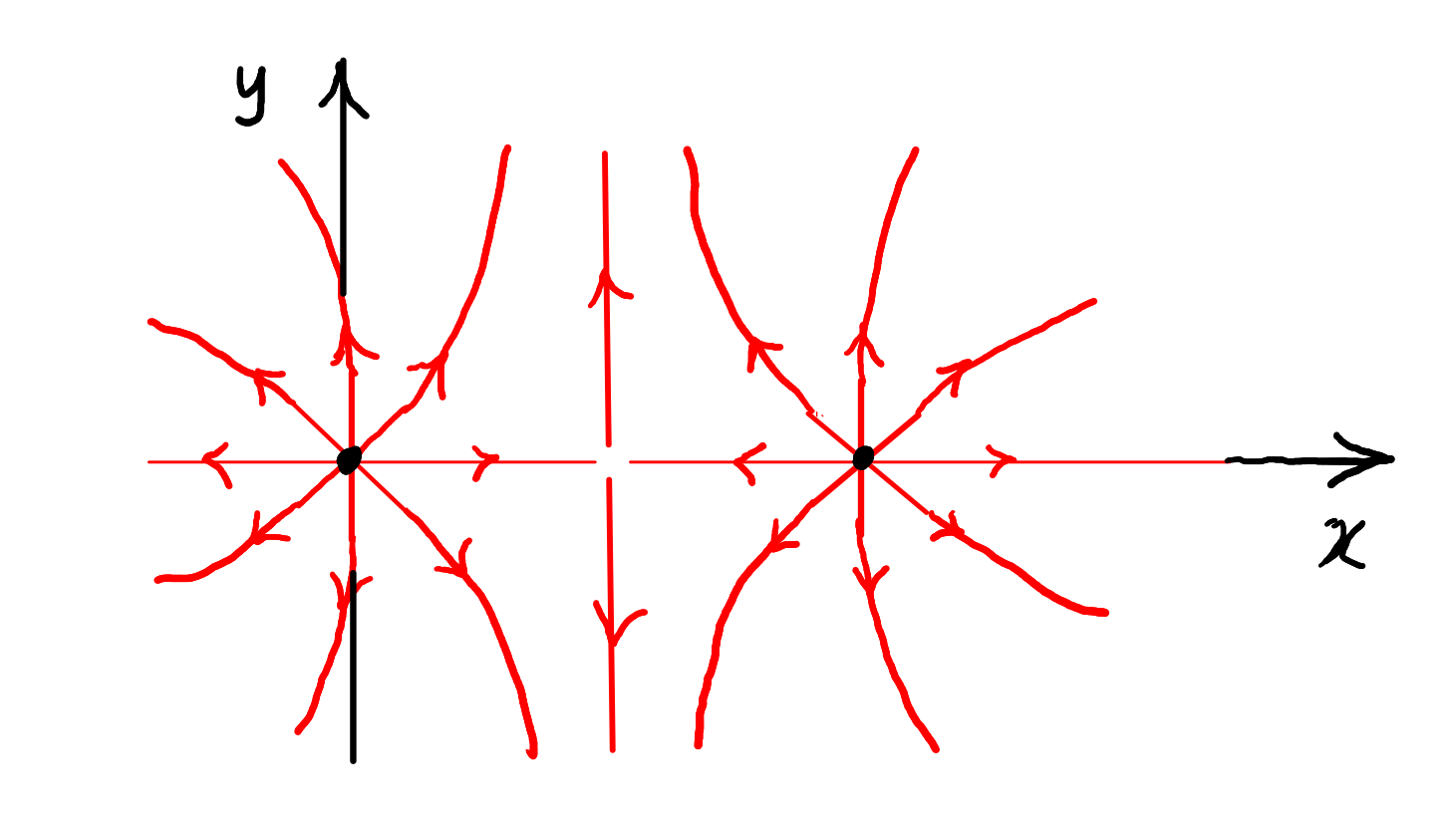
(b) Não há nenhum ponto de campo nulo.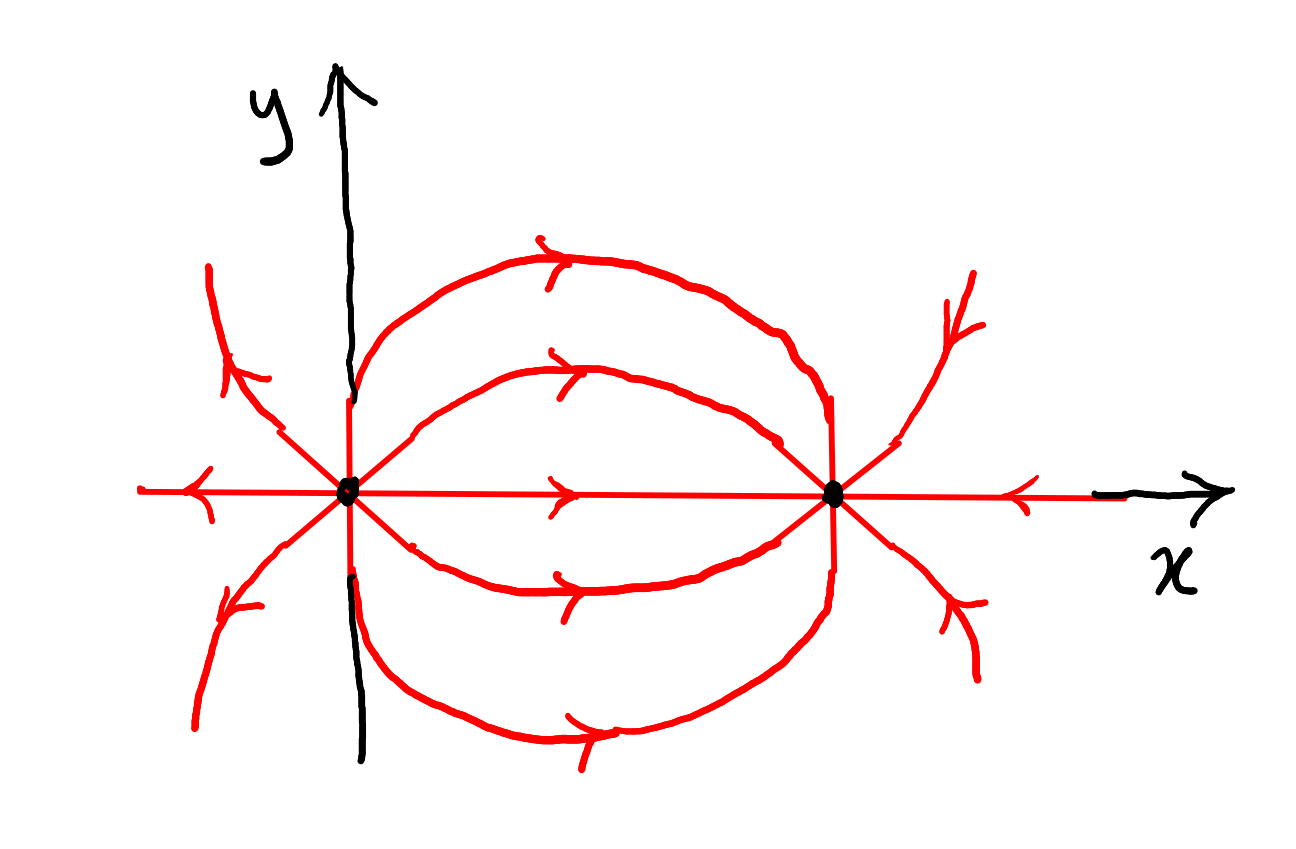
(c) O campo é nulo em.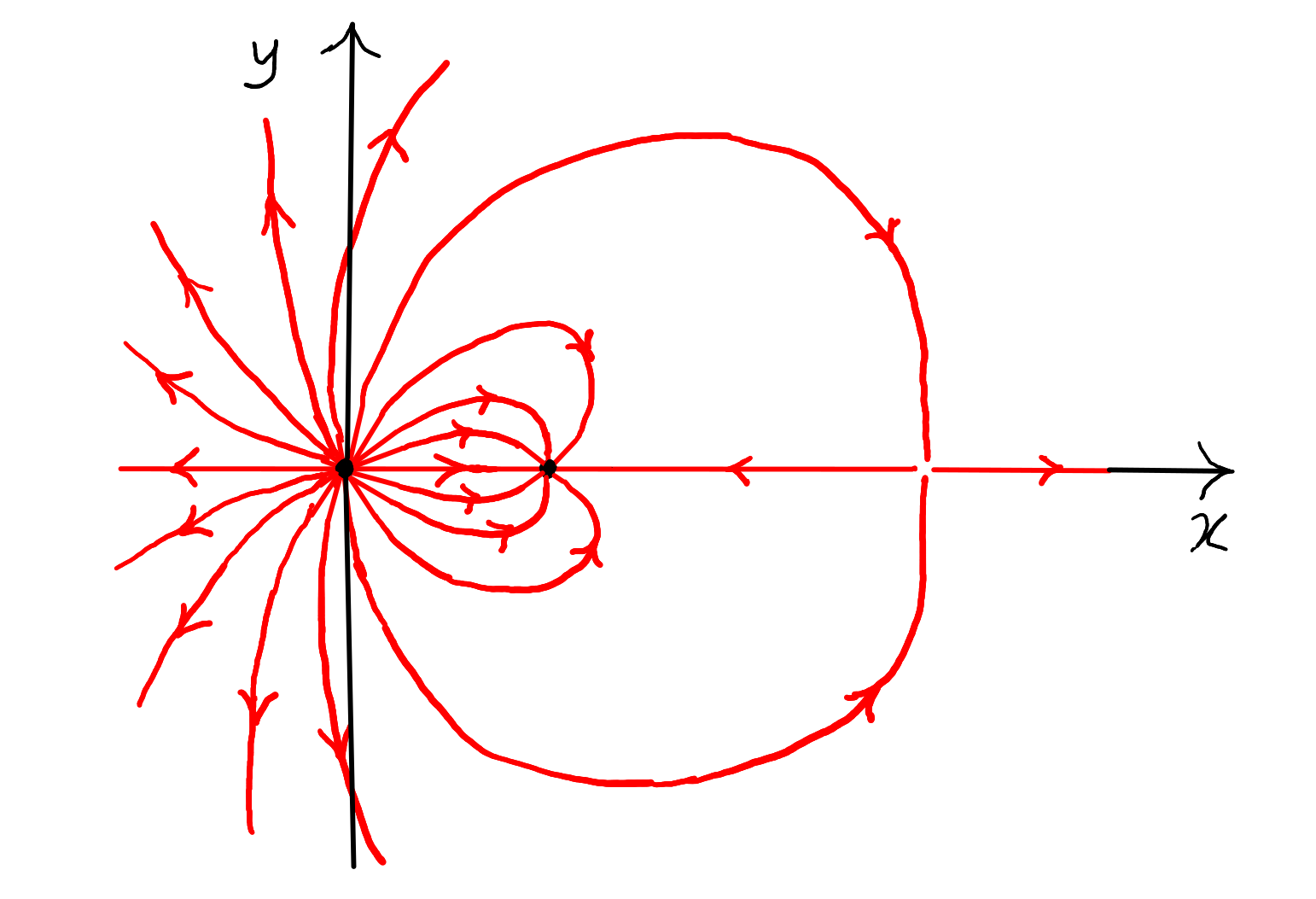
(d) O campo é nulo em..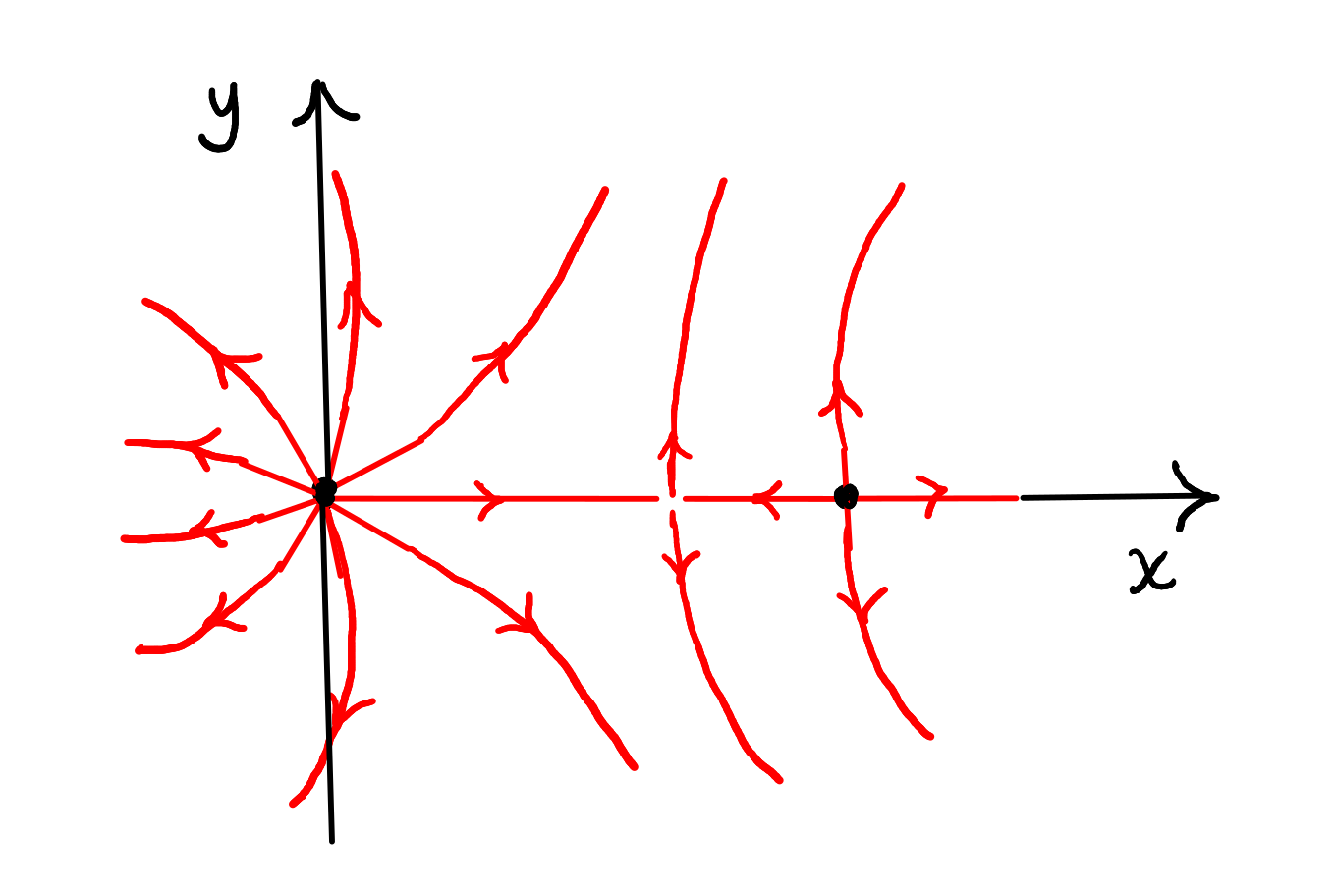
(e) Em qualquer sistema de duas cargas (exceto um dipolo) existe sempre um único ponto de campo nulo, situado na reta que passa pelas duas cargas. Ponto esse que estará sempre mais próximo da carga com menor valor absoluto. Se as duas cargas têm o mesmo sinal, o ponto de campo nulo estará no segmento que une as duas cargas; caso contrário, estará fora desse segmento e do lado da carga com menor valor absoluto. -
1.13.
N N.
-
1.14.
(a) . Como a força total é nula então o centro de massa do corpo permanece fixo.
(b) Como o binário das forças externas é não nulo, o dipolo roda em torno do seu centro de massa. O momento do binário faz rodar o dipolo e concomitantemente o momento dipolar de modo a este ficar com a direção e o sentido do campo elétrico exterior . -
1.15.
(a) .
(b) . -
1.16.
(a) ,
,
.
(b) : trajectória retilínea para ambos os casos. Para a partícula começa no ponto e segue uma trajetória retilínea paralela ao eixo até , enquanto que para a partícula começa no ponto seguindo uma trajetória retilínea paralela ao eixo no seu sentido positivo até , ponto no qual inverte o sentido do seu movimento passando a ter uma trajetória retilínea paralela ao eixo no seu sentido negativo até . -
1.17.
(a) As linhas saem da origem e entram no ponto (1, 0); no ponto (3, 0), onde o campo é nulo, as duas linhas na direção afastam-se do ponto e as duas linhas na direção aproxima-se dele.
(b) nC.
(c) mN. -
1.18.
(a) , , sendo a trajetória parabólica dada por para ambos os casos. A partícula começa o seu movimento na origem: para segue uma trajetória parabólica de concavidade côncava (parábola voltada para baixo), enquanto que para a sua trajetória é parabólica com concavidade convexa (parábola voltada para cima).
(b) . -
1.19.
A força elétrica é vezes maior do que o peso.
-
1.20.
A terceira carga é , e encontra-se entre as outras duas cargas, a uma distância da carga .
-
1.21.
e m/s.