2. Cálculo do campo elétrico

Carl Friedrich Gauss (1777–1855)
Uma região onde existe carga elétrica pode ser dividida em pequenas regiões e a carga em cada uma dessas regiões pode ser aproximada por uma carga pontual. No capítulo anterior mostrou-se a expressão vetorial do campo elétrico devido a uma carga pontual. O campo total produzido pela carga na região é obtido somando vetorialmente os campos de todas essas regiões.
Uma forma mais simples de obter o campo elétrico produzido pela carga numa região, em alguns casos em que a carga estiver distribuída de forma simétrica, consiste em usar a lei de Gauss, que é usualmente escrita usando o integral de superfície do campo elétrico (o fluxo elétrico). Escrita de forma diferencial, a lei de Gauss permite relacionar o campo elétrico num ponto com a carga na vizinhança desse ponto.
2.1 Campo de sistemas de cargas pontuais
A expressão (1.12) define o campo elétrico de uma carga pontual na origem. Para podermos usar essa expressão para várias cargas , , …, , teremos de começar por generalizar essa expressão ao caso de uma carga , que já não está na origem mas num ponto de vetor posição , como na figura 2.1.
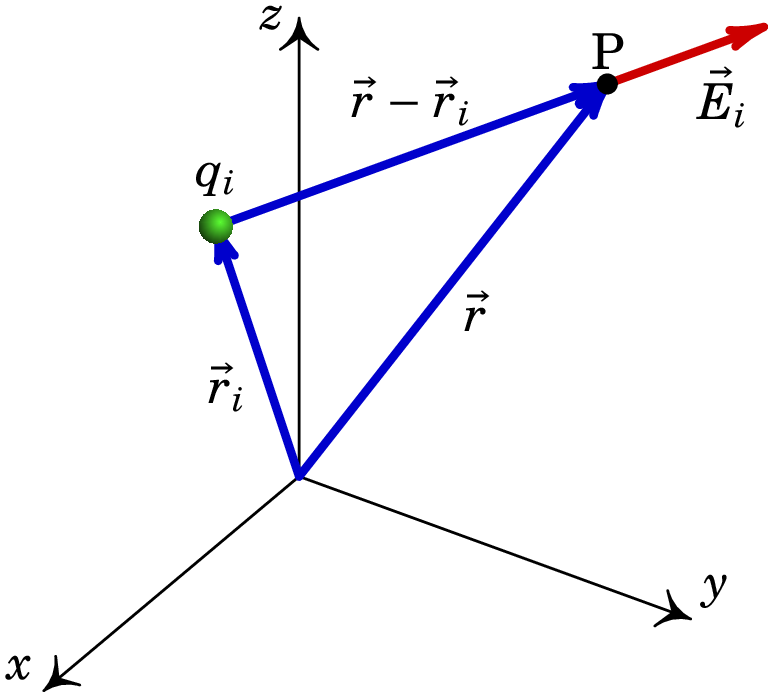
O vetor terá de ser substituído por , e a distância será agora . O versor radial esférico será substituído pelo versor que aponta na direção desde até o ponto P, que é:
| (2.1) |
Com essas alterações, o campo elétrico devido à carga é,
| (2.2) |
Por ser definido a partir da força elétrica, o campo elétrico também satisfaz o Princípio da Sobreposição, i.e., o campo elétrico total produzido por um conjunto de cargas pontuais (, …, ), é a soma dos campos produzidos por cada uma das cargas isoladamente:
| (2.3) |
e substituindo a expressão (2.2) para , o campo do sistema de cargas pontuais é,
| (2.4) |
Exemplo 2.1
Encontre o campo elétrico no ponto P, produzido pelas 3 cargas na figura.
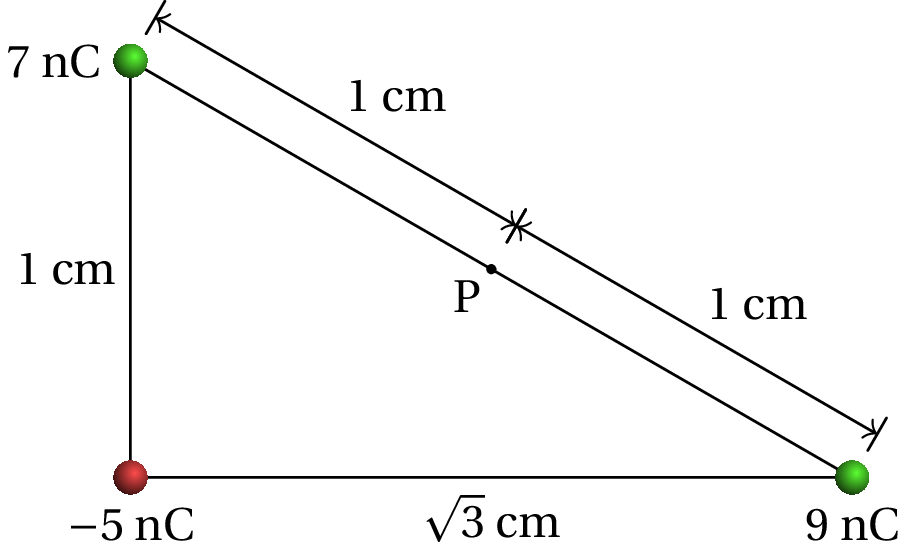
Resolução: As duas cargas positivas produzem campo divergente destas e a carga negativa produz campo convergente nesta. Os vetores dos campos produzidos pelas 3 cargas no ponto P são então como mostra a figura seguinte.
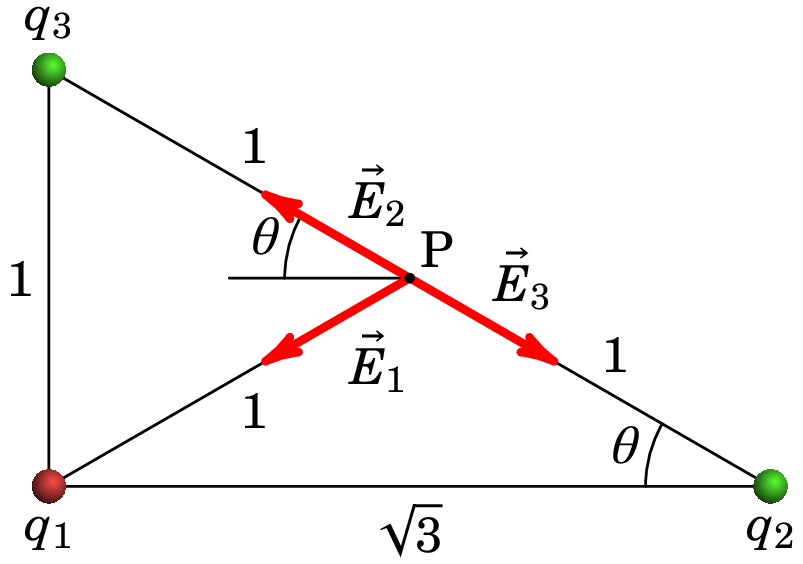
Usando as mesmas unidades do enunciado do problema (nC e cm),
Como tal, usaremos e os dados do enunciado, sem unidades. O campo assim calculado estará em mN/nC.
O módulo do campo produzido por cada carga pontual , no ponto P, é igual a sobre a distância desde até o ponto P, ao quadrado.
Como o ponto P está no meio da hipotenusa, as distâncias e são iguais a 1. E como a projeção da hipotenusa na base do triângulo é o segmento entre e , a projeção do ponto P está no meio desse segmento e a distância também é igual a 1. Os módulos dos campos são,
Observando o diagrama dos campos, as componentes vetoriais dos 3 campos são:
O campo total em P é a soma desses 3 vetores e, como e , obtém-se:
finalmente, substituem-se os módulos dos três campos elétricos
Este problema também podia ser resolvido substituindo na equação (2.4) os valores (confira):
2.2 Distribuições contínuas de carga
Para calcular o campo elétrico num ponto P, com vetor posição , produzido por uma carga distribuída continuamente numa região do espaço, divide-se essa região em sub-regiões (), cada uma com carga suficientemente pequena para que possa ser considerada como uma carga pontual. Seja a carga de cada sub-região tal que . Seja também o vetor posição de cada uma dessas sub-regiões . O vetor desde a região até o ponto P é e o versor na direção e com o sentido deste vetor é (ver figura 2.2).
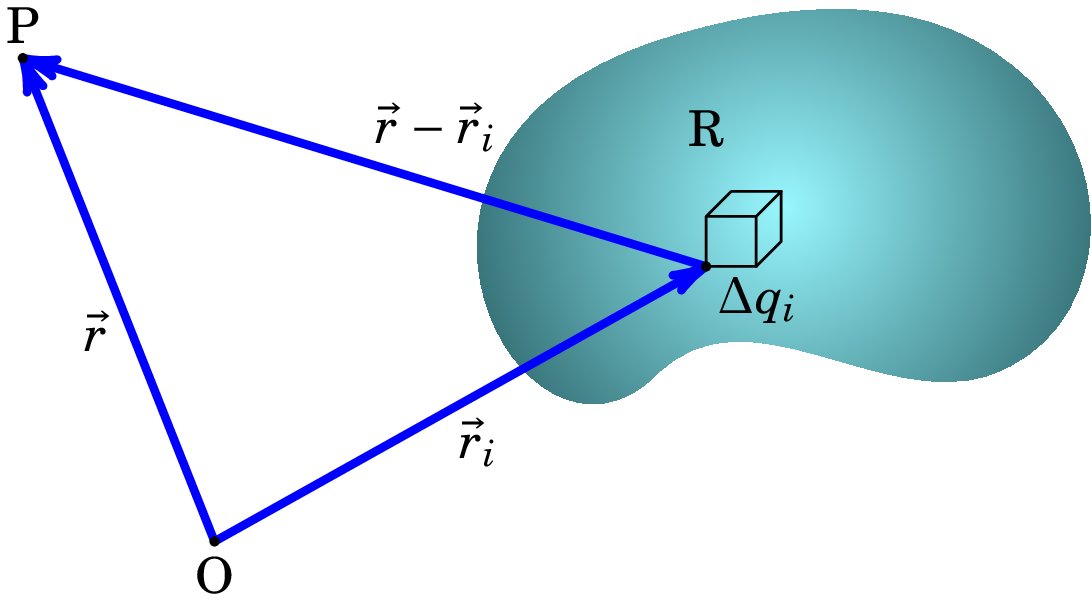
A expressão (2.4) para um sistema de cargas pontuais será uma boa aproximação para o campo elétrico no ponto P:
| (2.5) |
A aproximação torna-se exata no limite . Neste limite, a carga de cada região torna-se num elemento infinitesimal de carga , os vetores posição tornam-se num contínuo de vetores posição identificando todos os pontos da região carregada R e o somatório torna-se num integral sobre toda a região R onde existe carga:
| (2.6) |
O integral será integral de linha, de superfície ou de volume, conforme a carga estiver distribuída numa linha, superfície ou volume, respetivamente. Nas duas secções seguintes mostram-se exemplos do cálculo do campo elétrico devido a distribuições lineares e superficiais de carga.
2.2.1 Carga distribuída numa linha
No caso de cargas distribuídas ao longo de um fio (figura 2.3), a carga infinitesimal num pedaço de fio entre os pontos nas posições e é diretamente proporcional ao comprimento infinitesimal desse pedaço de fio:
| (2.7) |
onde é uma função que, em geral, depende de ponto para ponto no fio (note que cada ponto do fio é identificado pelo seu vetor posição ), chamada função densidade linear de carga, a qual é igual à carga por unidade de comprimento no ponto de vetor posição do fio, sendo a sua unidade SI igual a C/m.
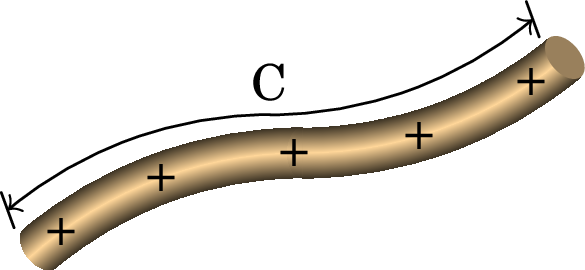
A equação vetorial de uma linha contínua é uma expressão para em função de um único parâmetro real , que determina a posição dos pontos na linha. Cada possível valor do parâmetro determina a posição de um ponto da linha e pode ser, e.g., um ângulo, um comprimento ou um instante de tempo; é a variação do vetor devida ao aumento infinitesimal do parâmetro para e é sempre tangente à linha. O comprimento infinitesimal de arco, , é então igual ao módulo do vetor . O integral em (2.6) é um integral de linha ao longo da linha C que segue o fio:
| (2.8) |
Trata-se de uma aproximação, porque o fio não é uma linha mas sim um sólido. A aproximação será mais exata tanto quanto menor for a secção transversal do fio. Realmente existem muitos percursos possíveis dentro do fio, sendo necessário usar um percurso médio para calcular o integral de linha. No limite em que a secção transversal do fio tende para zero a expressão (2.8) torna-se exata.
Exemplo 2.2
Um anel circular de raio tem carga total , distribuída uniformemente. Determine a expressão do campo elétrico ao longo do eixo longitudinal do anel (eixo perpendicular ao plano do anel e que passa pelo seu centro).
Resolução: Método 1. O anel tem densidade linear de carga . Convém escolher a origem no centro do anel e um dos eixos ao longo do eixo do anel, como na figura seguinte, em que o eixo dos é o eixo do anel e os outros dois eixos encontram-se no plano deste.
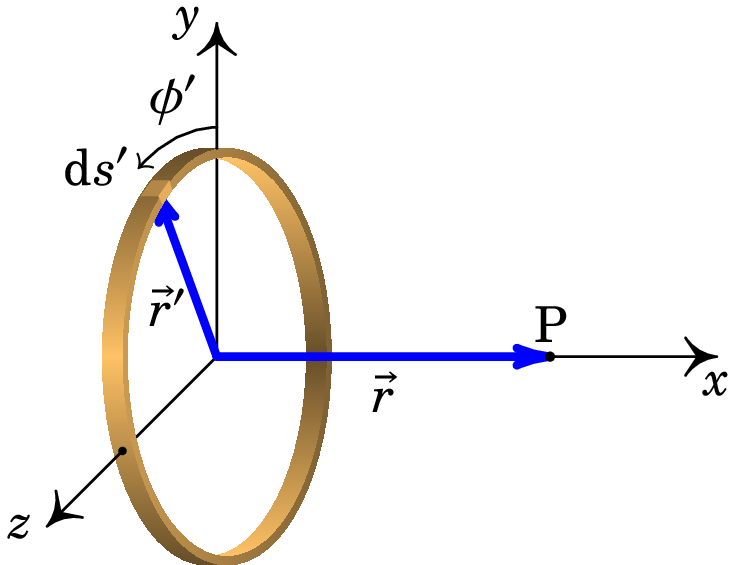
O anel é dividido em pedaços infinitesimais, de comprimento (ver figura). A vetor posição de cada pedaço infinitesimal do anel pode ser dado apenas em função do ângulo , medido no plano , desde o eixo :
onde ( é a variável de integração). O pedaço infinitesimal é um arco de raio , compreendido entre e , ou seja,
Como os integrais do seno e do cosseno, entre 0 e são nulos,
| (2.9) |
Resolução: Método 2. A figura seguinte mostra os campos produzidos por dois segmentos infinitesimais do anel, que se encontram em dois pontos do anel diametralmente opostos.
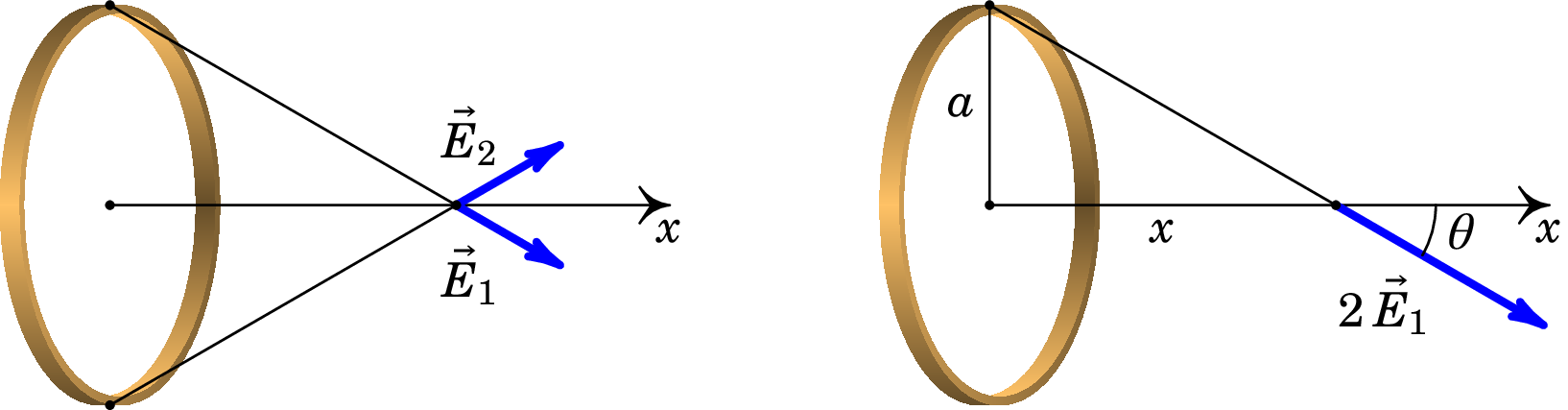
As componentes desses dois campos perpendiculares ao eixo do anel anulam-se e as componentes paralelas ao anel somam-se. Assim sendo, as cargas nesses dois segmentos podem ser colocadas no mesmo lado do anel, produzindo um campo duas vezes maior que o campo do primeiro segmento e a projeção desse campo ao longo do eixo do anel é igual à resultante dos dois campos iniciais.
O mesmo procedimento pode ser feito com todos os segmentos do anel e, como a componente do campo ao longo do eixo será a mesma independentemente da posição do segmento no anel, todas as cargas do anel podem ser concentradas numa única carga pontual colocada na posição do lado direito na figura acima e o campo total será a projeção do campo produzido por essa carga pontual ao longo do eixo.
O quadrado da distância desde essa carga pontual até o ponto P é igual a e o módulo do campo elétrico devido a essa carga é:
O módulo do campo do anel obtém-se multiplicando pelo cosseno do ângulo , que é igual a sobre
O campo elétrico no eixo do anel aponta na direção desse eixo, afastando-se (divergindo) do anel se ou aproximando-se (convergindo) no anel se .
2.2.2 Carga distribuída numa superfície
Quando a carga está distribuída continuamente numa lâmina fina (ver figura 2.4), o integral do campo pode ser aproximado por um integral de superfície. Neste caso, a carga infinitesimal numa sub-região de área infinitesimal é dada por:
| (2.10) |
onde é a densidade superficial de carga (carga por unidade de área) no ponto de vetor posição da lâmina, sendo a sua unidade SI igual a C/m.

Como tal, a expressão (2.6) para o campo conduz a um integral de superfície sobre a superfície S da lâmina:
| (2.11) |
O integral de superfície para o campo é uma aproximação já que as partículas com carga não podem ocupar uma superfície sem espessura, mas sim um volume no espaço. A aproximação será mais exata tanto quanto menor for a espessura da camada onde estão as cargas (ver figura 2.4).
O integral é um integral duplo, em ordem aos dois parâmetros que sejam usados para definir a superfície S parametricamente. A equação vetorial da uma expressão para o vetor posição em função de dois parâmetros reais e . O elemento infinitesimal de área é igual à área da superfície descrita pelo vetor quando aumenta para e aumenta para .
Se a superfície for plana, definem-se dois dos eixos cartesianos, por exemplo e , sobre a superfície e o elemento infinitesimal de área é . O apêndice A mostra como será o elemento infinitesimal de área em outros sistemas de coordenadas, quando uma das coordenadas é constante (equações (A.41), (A.50), (A.60), (A.61) e (A.62)).
Exemplo 2.3
Determine a expressão do campo elétrico ao longo do eixo longitudinal de um disco plano de raio e com carga total , distribuída uniformemente sobre a sua superfície.
Resolução. A densidade superficial de carga, constante, é igual a . Usaremos coordenadas polares (ver secção A.2.2) na superfície do disco (onde há carga) com origem no centro do disco, juntamente com um eixo normal segundo o eixo longitudinal do disco, o qual contém o ponto P onde se calcula o campo elétrico, tal como mostra a figura seguinte:
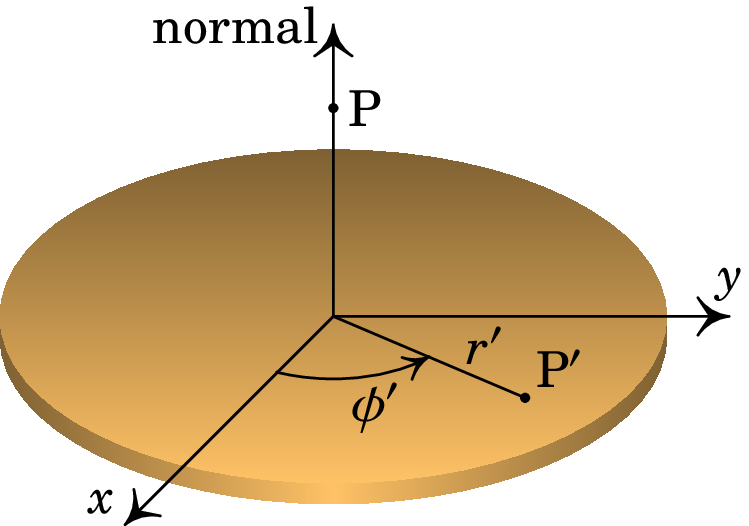
O respetivo elemento infinitesimal de área é (equação (A.41))
Os vetores posição dos pontos P sobre o eixo normal a uma distância do disco e do ponto P sobre o disco são, respetivamente, dados por:
onde é o versor normal ao plano, o qual aponta para fora do disco, no lado em que estiver o ponto P. A distância entre os pontos P e é:
Substituindo na equação (2.11) obtém-se
Os integrais de e , entre 0 e , são ambos nulos e o integral do termo que não depende de é igual a ; como tal,
Notando que
onde é uma constante de integração, o resultado final, tendo em conta que , é:
| (2.12) |
onde é a distância de um ponto no eixo longitudinal do disco até ao disco.
2.2.3 Carga distribuída num volume
No caso mais geral, a carga encontra-se distribuída dentro de um volume. A carga infinitesimal dentro de uma sub-região com volume infinitesimal é dada por:
| (2.13) |
onde é a densidade volúmica de carga (carga por unidade de volume) no ponto de vetor posição , sendo a sua unidade SI igual a C/m.
Esse integral triplo costuma ser difícil de calcular analiticamente; os casos em que é possível obter um resultado analítico acontecem quando existe alguma simetria na forma como a carga está distribuída no espaço. Nesses casos, é possível calcular o campo elétrico usando a lei de Gauss, como veremos nas próximas secções. Para poder enunciar a lei de Gauss, começaremos por introduzir o conceito de fluxo elétrico na próxima secção.
No próximo capítulo veremos também que o campo elétrico pode ser obtido a partir do potencial, que pode ser mais fácil de calcular quando for necessário resolver um integral triplo. Como tal, não mostraremos nenhum exemplo de utilização da equação (2.14).
2.3 Fluxo elétrico
O campo elétrico pode ser compreendido melhor usando o conceito de fluxo. Define-se o fluxo elétrico por analogia com um fluido incompressível. No escoamento do fluido, as linhas de campo são tangentes à velocidade do fluido em cada ponto e o fluxo do campo de velocidades é igual ao volume de fluido que passa através duma superfície, por unidade de tempo.
Através de uma superfície de área , perpendicular à velocidade do fluido, e se o módulo da velocidade, , for constante em todos os pontos dessa superfície, o volume de fluido que passa através da superfície, por unidade de tempo, é igual a . A figura 2.5 mostra dois exemplos de superfícies perpendiculares às linhas de campo elétrico e com módulo do campo constante em toda a superfície.
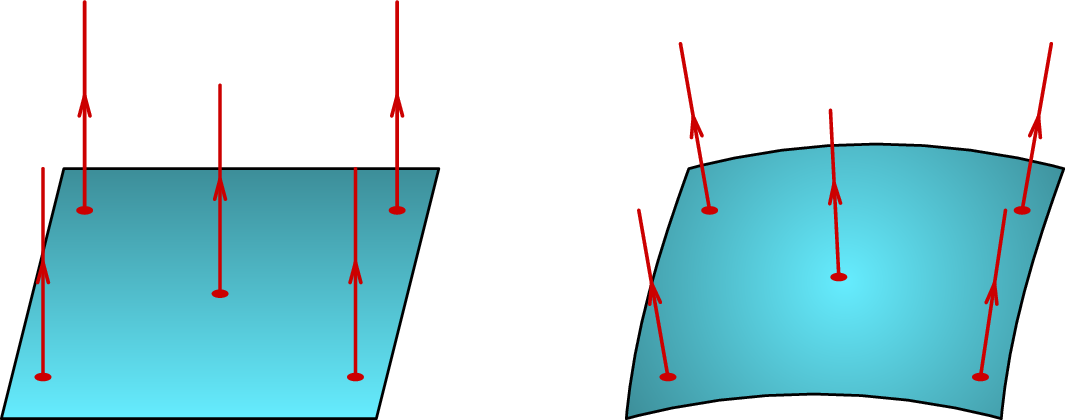
Por analogia com o fluxo do fluido, no caso dessas duas superfícies na figura 2.5 define-se o fluxo elétrico através da superfície igual ao produto do módulo do campo vezes a área da superfície:
| (2.15) |
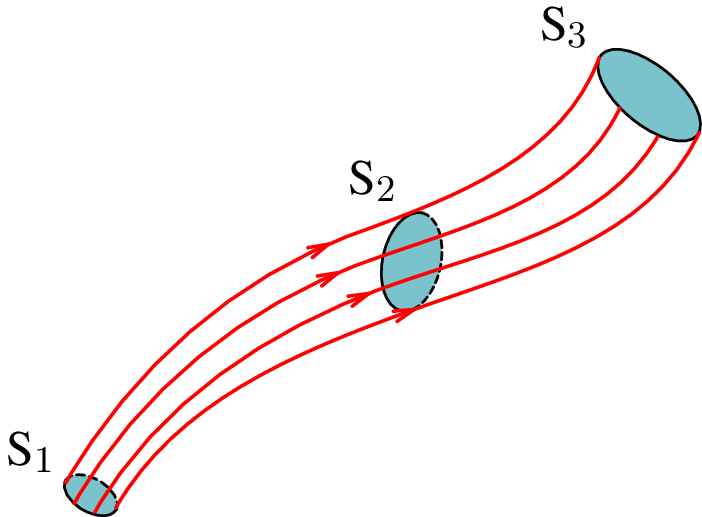
O volume delimitado pelas linhas de campo que passam por uma curva fechada, e.g., a fronteira da superfície na figura 2.6, chama-se tubo de fluxo. Usando a analogia com o fluido incompressível, se não existem dentro do tubo pontos onde entra ou sai fluido, então o fluxo é o mesmo em todas as secções transversais do tubo, independentemente da curvatura ou inclinação dessas secções. Por exemplo, no tubo de fluxo da figura 2.6, o volume de fluido que passa pelas três superfícies , e , por unidade de tempo, deve ser o mesmo e, como tal, o fluxo através dessas superfícies, ou de qualquer outra secção do tubo, é igual.
Essa propriedade dos tubos de fluxo pode usar-se para calcular o fluxo de um campo elétrico uniforme, , através de uma superfície plana de área , que não seja perpendicular às linhas de campo. O ângulo de inclinação das linhas de campo em relação ao versor normal à superfície, , é na figura 2.7. O fluxo através da superfície inclinada é igual ao fluxo através da projeção dessa superfície no plano perpendicular às linhas de campo, ou seja através da superfície a tracejado na figura 2.7, que faz um ângulo com a superfície inclinada. Os dois fluxos são iguais porque a superfície inclinada e a superfície a tracejado fazem parte do mesmo tubo de fluxo, formado pelas linhas de campo que as atravessam.
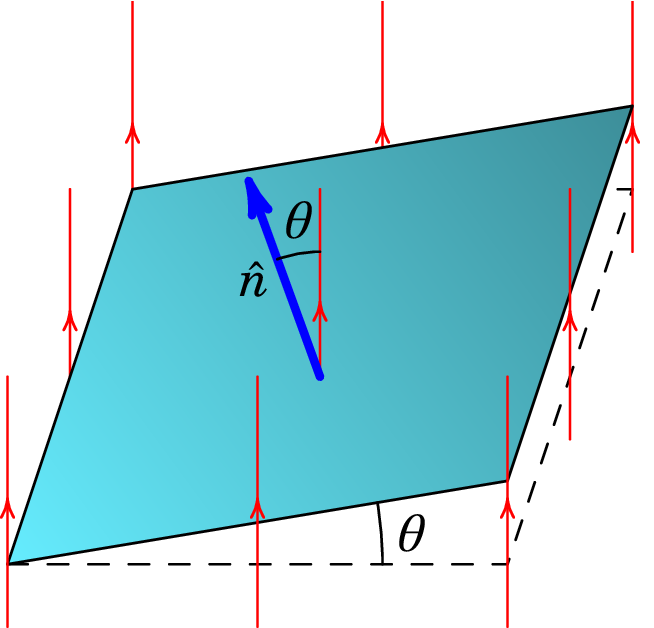
A área da superfície a tracejado é , onde é ângulo entre o campo e a perpendicular ao plano (figura 2.7). Como essa superfície a tracejado sim é perpendicular às linhas de campo, o fluxo através dela é igual ao módulo do campo vezes a sua área:
| (2.16) |
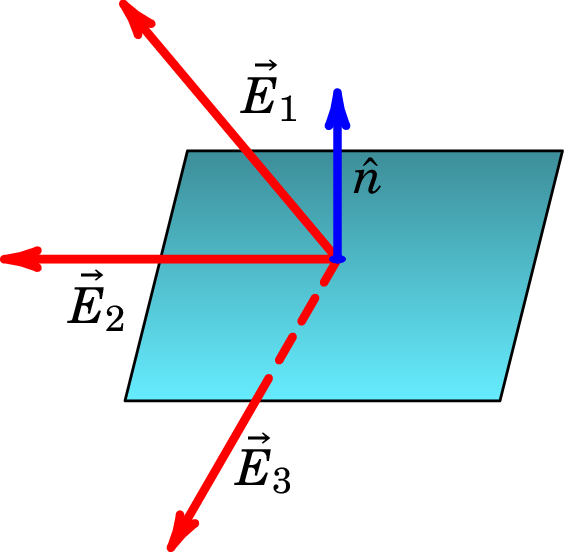
A figura 2.8 mostra três possíveis campos na superfície. O campo faz um ângulo agudo com o versor normal e, por isso, produz fluxo positivo, ou seja, fluxo que passa no mesmo sentido do versor normal. O campo é perpendicular à superfície e, como tal, o seu produto escalar com o versor normal é nulo e esse campo não produz nenhum fluxo. Finalmente, o campo faz um ângulo obtuso com o versor normal, produzindo assim fluxo negativo, ou seja, fluxo no sentido oposto do versor normal.
O produto escalar é a componente do campo na direção normal à superfície. Como tal, o fluxo elétrico é a componente normal do campo vezes a área da superfície.
No caso de campos não uniformes e superfícies curvas, divide-se a superfície em segmentos com áreas (), como na figura 2.9. Se o número de segmentos for elevado e cada um deles for suficientemente pequeno, podem ser aproximados por pequenos planos.
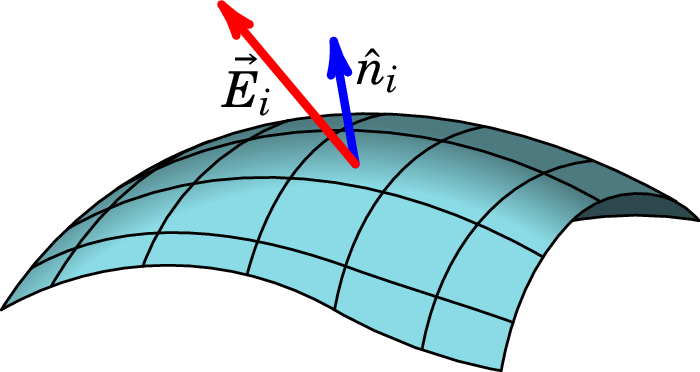
No plano infinitesimal de área o campo será , aproximadamente constante, de forma que o fluxo nele é dado pela equação (2.16). O fluxo total na superfície é igual à soma de todos os fluxos nos pequenos planos.
| (2.17) |
A aproximação torna-se exata no limite em que se aproxima de infinito. Essa soma de uma função (neste caso a componente normal do campo) vezes a área da superfície é um integral de superfície, escrito da forma seguinte:
| (2.18) |
O integral de superfície na equação (2.18) é um integral duplo. Escolhendo um sistema de coordenadas apropriado, a superfície S poderá corresponder a um valor constante de uma das 3 coordenadas e, nesse caso, as variáveis de integração serão as outras duas coordenadas (veja as equações (A.41), (A.50), (A.60), (A.61) e (A.62) no apêndice A). No caso mais geral seria necessário parametrizar a superfície S com dois parâmetros e , que seriam as variáveis de integração.
Exemplo 2.4
Determine o fluxo elétrico através da superfície esférica de raio e centro na origem, devido ao campo elétrico .
Resolução. Em coordenadas esféricas (, , ) (secção A.2.4 no apêndice A), na superfície esférica a coordenada é constante, , e o elemento infinitesimal de área é (equação (A.60))
O vetor posição dos pontos na superfície esférica é (equação (A.58))
O versor normal à superfície esférica é o próprio versor
E o campo sobre a superfície esférica obtém-se substituindo na expressão do campo pela coordenada da superfície esférica
A componente do campo normal à superfície esférica é
O fluxo elétrico é
O resultado positivo indica que existe fluxo a sair da esfera, já que o versor usado aponta para fora da esfera.
2.4 Lei de Gauss
Como vimos no início do capítulo, o campo elétrico de uma distribuição de carga é a sobreposição dos campos produzidos por muitas cargas pontuais. Convém então analisar o fluxo elétrico produzido pelo campo de uma única carga pontual. Em relação a uma superfície S fechada, a carga pode estar ou fora ou dentro dessa superfície, tal como mostra a figura 2.10. Se a carga estiver fora, apenas algumas linhas de campo atravessam a superfície; se a carga estiver dentro de S, todas as linhas de campo a atravessam.
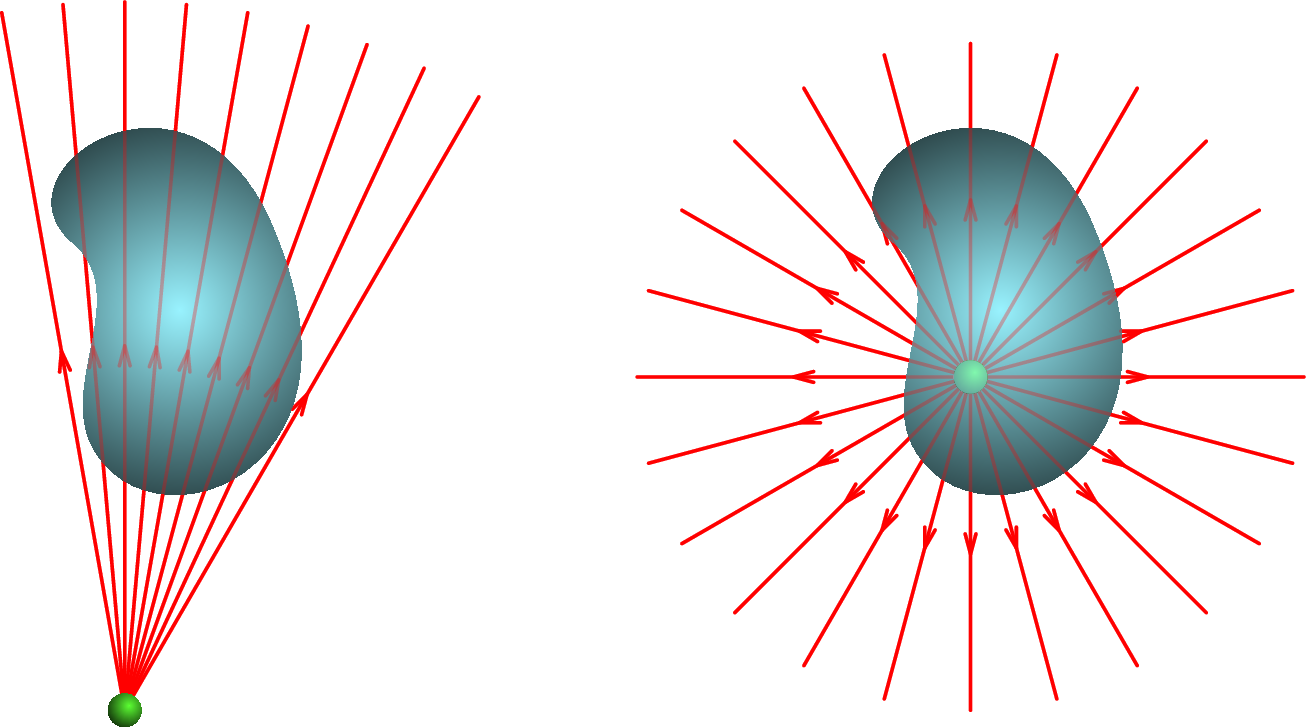
Quando a carga pontual está dentro da superfície S, qualquer esfera com centro na carga também é atravessada por todas as linhas de campo elétrico e, como tal, encontra-se no mesmo tubo de fluxo de S (figura 2.11). O fluxo elétrico através de S pode ser determinado calculando o fluxo que atravessa a esfera. No lado direito da figura 2.11 mostra-se o campo num ponto da esfera.

Na superfície esférica, o campo é sempre perpendicular e o seu módulo é sempre igual a , onde é o raio da esfera. Como tal, o fluxo na esfera pode obter-se usando a equação (2.15). A área da esfera é , e multiplicando pelo módulo do campo obtém-se o fluxo:
| (2.19) |
Ou seja que, o fluxo total produzido pela carga pontual , através de qualquer superfície fechada em que a carga esteja no interior, é sempre , independentemente do tamanho e da forma da superfície. No caso de superfícies fechadas, é habitual calcular-se sempre o fluxo para fora da superfície. Com essa convenção, o sinal da carga dá o sinal correto do fluxo na expressão ; se a carga for positiva há fluxo para fora da superfície, mas se a carga for negativa o fluxo será para dentro dela.
Se a carga está fora de S, as linhas de campo que atravessam a superfície estão dentro de um ângulo sólido , menor que o ângulo total da esfera toda (figura 2.12). Se imaginarmos que a carga é uma fonte de luz, esse ângulo sólido é a sombra projetada pela superfície S numa esfera; uma parte, ,da superfície estará iluminada e a outra parte, , estará na escuridão. Se for positiva, pela superfície entra fluxo elétrico e esse mesmo fluxo sai todo pela superfície ; se for negativa, o mesmo fluxo que entra por sai por . Como tal, o fluxo total através de S é nulo.
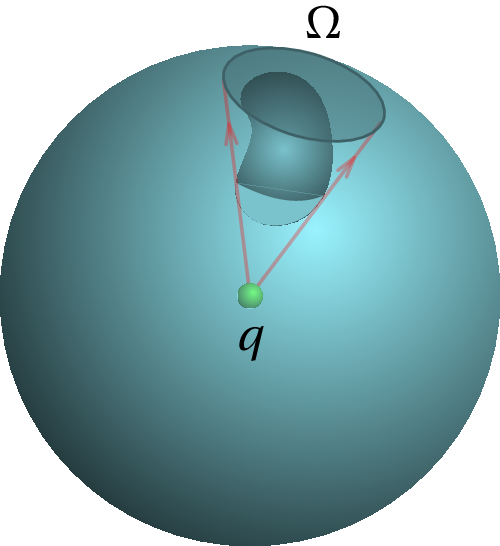
Conclui-se então que o fluxo elétrico devido a uma carga pontual é nulo em qualquer superfície fechada, se a carga estiver fora da superfície, e igual a se a carga estiver dentro da superfície.
Uma distribuição de carga pode ser dividida em várias cargas pontuais , , …, , e o fluxo total através de uma superfície fechada S será igual à soma dos fluxos produzidos por cada uma das cargas pontuais. As cargas que se encontram no exterior de S não produzem fluxo, e cada carga que esteja dentro de S produz fluxo . Como tal, o fluxo total através da superfície fechada S é:
| (2.20) |
onde é a carga total no interior da superfície S fechada. Esta equação chama-se lei de Gauss:
O fluxo elétrico através de qualquer superfície fechada é igual ao valor da carga total no interior da superfície vezes .
Se a carga total no interior for positiva, o fluxo é positivo, indicando que há linhas de campo a sairem da superfície. Se a carga total for negativa, o fluxo é negativo porque há linhas de campo a entrarem na superfície.
O lado direito na lei de Gauss também costuma ser escrito , onde é denominada permitividade elétrica do vácuo (ver Apêndice C), a qual é igual a
| (2.21) |
No Capítulo 1 vimos que em alguns sistemas de cargas pontuais é possível desenhar em cada carga um número de linhas de campo proporcional à carga. Nesses casos, o fluxo elétrico numa região é proporcional ao número de linhas de campo que atravessam essa região. Por exemplo, na figura do exemplo 1.3 as 8 linhas de campo a saírem da carga do lado esquerdo equivalem a 8 unidades de fluxo, e as 18 linhas da outra carga correspondem a 18 unidades de fluxo.
Como veremos a seguir, a lei de Gauss revela-se particularmente útil na determinação do campo elétrico produzido por sistemas com distribuição de carga que apresentam uma dada simetria. Em particular, analisaremos sistemas com simetria plana, esférica e cilíndrica.
Exemplo 2.5
Um eletrão encontra-se no centro de um cubo cuja aresta mede nm. Determine o fluxo elétrico através de uma das faces do cubo.
Resolução. O fluxo através da superfície, fechada, do cubo obtém-se a partir da lei de Gauss:
A carga interna é a carga do eletrão ( C). Assim, o fluxo total através da superfície do cubo é:
Por simetria, o fluxo através de cada face deve ser o mesmo, pelo que o fluxo numa face é a sexta parte do fluxo total no cubo: nN·m/C. Os sinais negativos dos resultados obtidos indicam que o fluxo é para dentro do cubo. Como a carga do eletrão é negativa, o campo elétrico do electrão converge neste, pelo que o fluxo é negativo.
2.4.1 Simetria plana
Existe simetria plana em sistemas para os quais nada se altera quando são sujeitos a um qualquer deslocamento ao longo de um plano.
No caso de uma distribuição de carga, o único caso em que isso acontece é se houver densidade superficial de carga , constante, num plano infinito. Qualquer deslocamento desse plano sobre si próprio não altera o sistema.
É claro que se trata de uma situação hipotética, já que não pode existir um plano infinito com carga infinita, mas o resultado poderá ser uma boa aproximação em alguns casos. Como o sistema não se altera sob qualquer deslocamento do plano sobre si próprio, as linhas do campo elétrico que ele produz também não podem sofrer alteração. Conclui-se então que as linhas de campo elétrico deverão ser perpendiculares a um plano infinito.
A invariância sob os deslocamentos do plano implica também que todos os pontos que estiverem à mesma distância deverão ser equivalentes. Como tal, nesses pontos o módulo do campo deverá ser igual. O módulo do campo poderá depender apenas da distância ao plano.
Exemplo 2.6
Determine a expressão do campo elétrico devido a um plano infinito com densidade superficial de carga constante.
Resolução. Como exite simetria plana, as linhas de campo elétrico serão perpendiculares ao plano , como mostra a figura seguinte
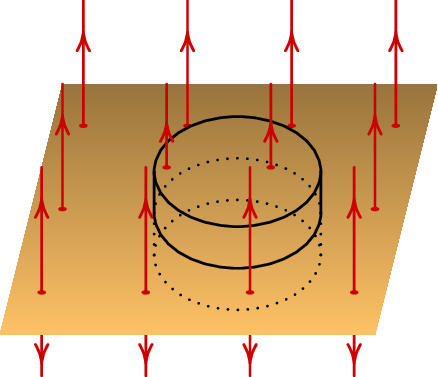
Seja S a superfície de um cilindro com tampas de área paralelas ao plano, à mesma distância em cada lado do plano, como na figura acima. Não existe fluxo nas paredes laterais do cilindro, porque são tangentes às linhas de campo. Nas duas tampas do cilindro o campo tem o mesmo módulo , por estarem á mesma distância do plano. Se sai fluxo pelas duas tampas e se entra fluxo pelas duas. Como tal, o fluxo total em S é a soma dos fluxos nas duas tampas, que são iguais e podem ser calculados com a equação (2.15):
A carga no interior de S é , e aplicando a lei de Gauss obtém-se
Concluindo, o único exemplo de simetria plana que consideramos é um plano infinito com densidade superficial de carga constante, que produz um campo uniforme dado por:
| (2.22) |
onde é o versor normal ao plano. Como esse versor aponta no sentido que se afasta do plano nos dois lados, quando a carga for positiva o campo é no sentido que se afasta do plano nos dois lados e quando a carga é negativa o campo é no sentido que se aproxima do plano nos dois lados. Observe-se que a constante pode ser escrita também como .
Num condutor plano finito, de área e com carga total , a carga distribui-se sobre a superfície do plano, mas essa superfície é composta por dois planos paralelos de área e as paredes laterais, de altura igual à espessura do plano. Como veremos na secção 3.8 do capítulo 3, a densidade superficial de carga será maior nas bordas do plano. No entanto a expressão (2.22), usando , é uma boa aproximação para um plano finito de dimensões lineares e na região onde as linhas de campo elétrico são aproximadamente paralelas, i.e., próximo do centro do plano e a uma distância, , muito menor do que as dimensões lineres do plano: e .
2.4.2 Simetria esférica
Existe simetria esférica quando qualquer rotação em torno de um ponto fixo não altera em nada um sistema. Esse será o caso de uma distribuição de carga com densidade de carga que depende apenas da distância a um ponto fixo. Por exemplo, uma superfície esférica com densidade superficial de carga constante.
Outros exemplos são uma carga pontual no centro de uma superfície esférica com densidade superficial de carga constante, várias superfícies esféricas, concêntricas, com densidades superficiais de carga diferentes, mas todas constantes, ou uma distribuição de carga dentro de uma esfera, com densidade volúmica de carga que depende apenas da distância até o centro da esfera ( pode ser constante ou não).
Devido à simetria esférica, as linhas de campo e o campo elétrico possuem a direção radial a partir do centro de simetria e, considerando coordenadas esféricas (secção A.2.4 no apêndice A) com a origem no centro de simetria, então o campo elétrico possui apenas componente radial esférica, sendo que esta apenas depende da distância ao centro de simetria, i.e., da coodenada radial esférica . Resumindo, dada a simetria esférica, o campo elétrico é da forma: .
Qualquer superfície esférica S, com centro no centro de simetria, será perpendicular às linhas de campo e é constante em S. Como tal, o fluxo elétrico através de uma superfície esférica S de raio será vezes a área da esfera, ou seja
| (2.23) |
e substituindo na lei de Gauss obtém-se
| (2.24) |
onde é a carga dentro da superfície esférica S, de raio e centro no centro de simetria.
Exemplo 2.7
Uma esfera maciça de raio tem carga total e densidade de carga constante. Determine o campo elétrico no interior e no exterior da esfera.
Resolução. A distribuição de carga apresenta simetria esférica. De modo a aplicar a Lei de Gauss, teremos de considerar duas superfícies esféricas e , com centro no centro da esfera, a primeira com raio maior que o raio da esfera e a segunda com raio menor que :
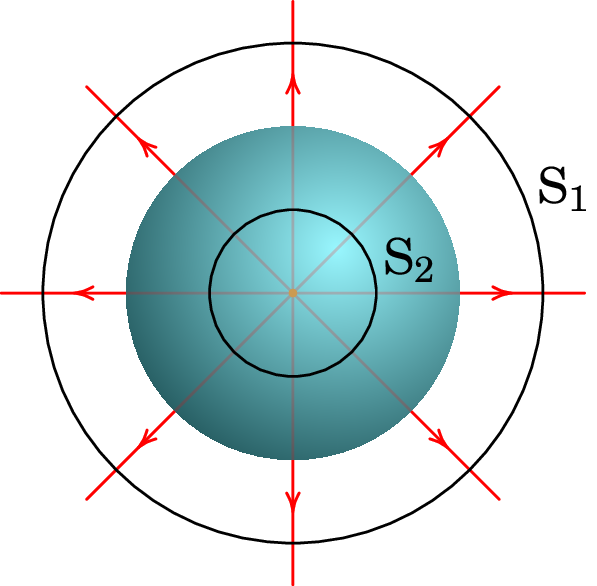
A carga no interior da superfície é a carga total da esfera: e a carga no interior da superfície é o seu volume vezes a densidade volúmica de carga:
Substituindo na equação (2.24) obtém-se a expressão da intensidade do campo. O campo, em coordenadas esféricas, é então dado por:
| (2.25) |
Neste exemplo considerou-se a carga total da esfera como sendo positiva (linhas de campo divergentes). Contudo, a expressão acima é válida para qualquer valor real de .
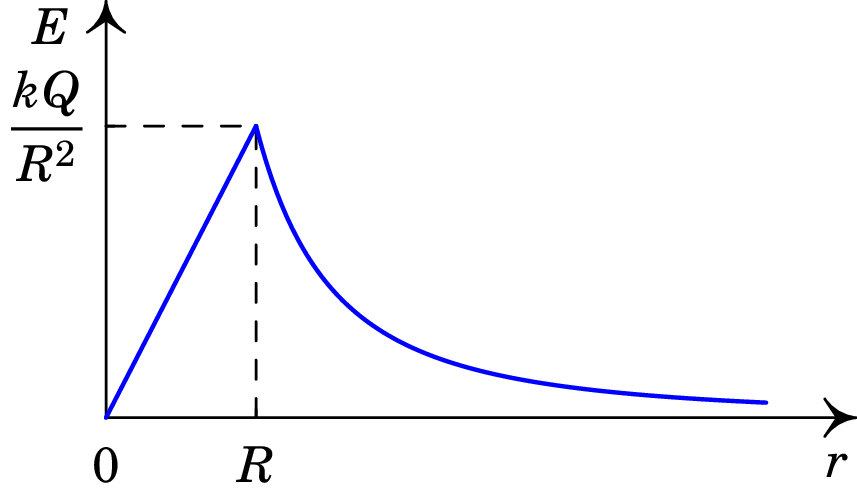
A figura 2.13 mostra o gráfico da intensidade do campo de uma esfera maciça com densidade volúmica de carga constante obtido no exemplo anterior (no caso em que ). Dentro da esfera a intensidade do campo aumenta de forma linear em função de e fora da esfera é inversamente proporcional ao quadrado de . Assim, fora da esfera, o campo elétrico é igual ao de uma carga pontual de carga igual à da esfera, , no centro da esfera — comparar com a expressão (1.12) e com a figura 1.11. O campo é na direção radial esférica.
2.4.3 Simetria axial
Existe simetria axial, ou cilíndrica, quando qualquer rotação em torno de um eixo fixo e qualquer translação ao longo desse eixo, não altera nada no sistema. Esse será o caso de uma distribuição de carga com densidade de carga que depende apenas da distância até o eixo de simetria. Por exemplo, uma superfície cilíndrica, com raio finito mas comprimento infinito, com densidade superficial de carga constante.
Outros exemplos são um fio retilíneo infinito com densidade linear de carga constante ou um cilindro de raio finito mas comprimento infinito com densidade de carga que depende unicamente da distância até o eixo do cilindro. Tal como no caso da simetria plana, não existe sistemas reais com este tipo de simetria, mas os sistemas hipotéticos com esta simetria dão resultados que podem ser uma boa aproximação em alguns casos reais.
As linhas de campo deverão ser na direção radial cilíndrica a partir do eixo de simetria. Em coordenadas cilíndricas (secção A.2.3 no apêndice A), considerando o eixo coincidente com o eixo de simetria, as linhas de campo elétrico são na direção do versor , o campo elétrico possui apenas componente radial cilíndrica, a qual poderá depender apenas da coordenada radial cilíndrica (distância até o eixo de simetria). Resumindo, devido à simetria axial, o campo elétrico é da forma: .
Seja S uma superfície cilíndrica fechada de raio e altura , cujo eixo longitudinal é coincidente com o eixo de simetria axial de uma dada distribuição de carga. As linhas de campo são tangentes às tampas (base e topo) da superfície S e, como tal, nas tampas não há fluxo. A superfície lateral curva da superfície S é perpendicular às linhas de campo e é constante na superfície lateral. A área dessa superfície curva é e o fluxo total através de S é:
| (2.26) |
e substituindo na lei de Gauss obtém-se
| (2.27) |
onde é a carga dentro da superfície cilíndrica S de raio e altura , coaxial com o eixo de simetria.
Exemplo 2.8
Determine a expressão do campo elétrico de um fio retilíneo infinito com densidade linear de carga, , constante.
Resolução. A linhas de campo elétrico têm simetria axial, tal como mostra a figura seguinte:
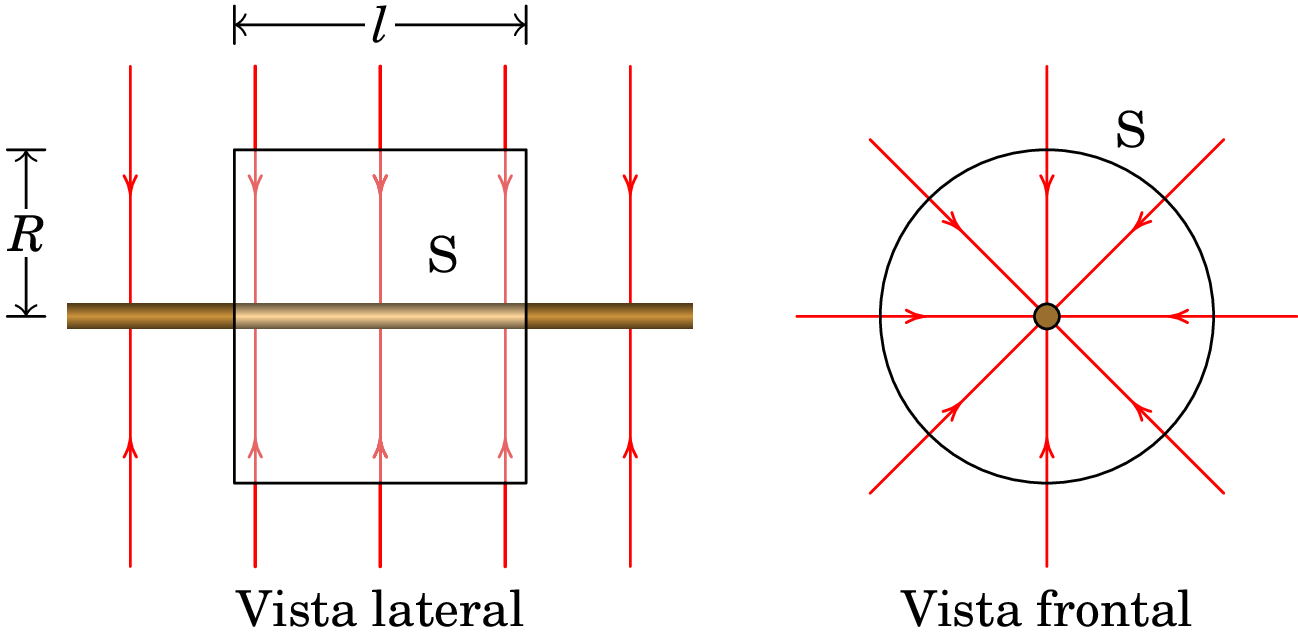
A carga no interior do cilindro S da figura anterior é
e substituindo na equação (2.27) obtém-se a intensidade do campo. A expressão vetorial do campo, em coordenadas cilíndricas, é então:
| (2.28) |
Neste exemplo considerou-se a densidade linear de carga como sendo negativa (linhas de campo convergentes). Contudo, a expressão acima é válida para qualquer valor real de .
2.5 Forma diferencial da Lei de Gauss
A lei de Gauss, na forma da equação (2.20), é uma equação integral. É útil também expressá-la na forma de uma equação diferencial, em função das derivadas do campo elétrico num ponto em vez do seu integral numa superfície.
No apêndice A define-se a divergência de forma geral (equação (A.71)) para qualquer campo vetorial. Se o campo vetorial for um campo elétrico, o integral de superfície na equação (A.71) segundo a lei de Gauss (2.20) será igual a , onde é a carga no interior da superfície fechada S, com volume . Como tal, a expressão da divergência do campo elétrico é:
| (2.29) |
No limite em que se aproxima de zero, o interior de S aproxima-se dum único ponto e o limite é igual à densidade volúmica de carga nesse ponto e é o mesmo que :
| (2.30) |
Esta é a forma diferencial da lei de Gauss.
A divergência de um campo vetorial é um campo escalar definido em cada ponto do espaço (ver apêndice A), pelo que a expresão (2.30) é também conhecida como lei de Gauss local. Conhecida a densidade volúmica de carga numa dada região, obtém-se a divergência do campo em qualquer ponto dessa região e vice-versa.
2.6 Natureza conservativa do campo elétrico
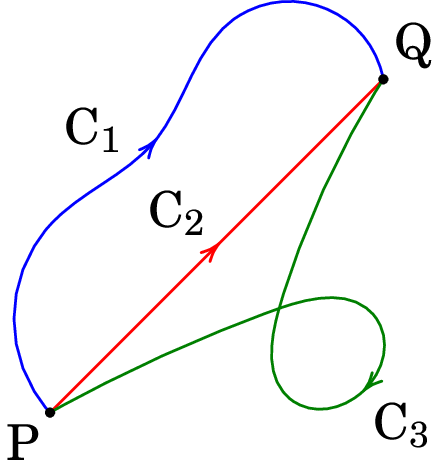
O campo elétrico produzido por cargas é um campo conservativo, i.e., o integral de linha do campo entre quaisquer dois pontos P e Q dá o mesmo valor, independentemente do percurso de integração usado.
No caso da figura 2.14, o integral de linha do campo conduz ao mesmo resultado ao longo de qualquer uma das três curvas, ou qualquer outra curva entre os pontos P e Q.
| (2.31) |
Para demonstrar que o campo elétrico é conservativo, começaremos por calcular os integrais na equação (2.31) no caso do campo elétrico produzido por uma carga pontual . Escolhendo a origem no ponto onde está a carga, em coordenadas esféricas o campo é
| (2.32) |
Nos integrais de linha da equação (2.31) cada curva deverá poder ser descrita por uma função vetorial contínua em função de um único parâmetro real . Isto significa que para cada valor do parâmetro , cada ponto da curva é identificado pelo vetor posição . Este procedimento é denominado por parametrização da curva . O vetor deslocamento infinitesimal é uma forma abreviada de se escrever:
| (2.33) |
e o integral é calculado em função do parâmetro entre os seus valores correspondentes aos dois pontos extremos de .
No caso da curva representada na figura 2.15, o integral de linha calcula-se usando a expressão (A.59) do deslocamento infinitesimal em coordenadas esféricas: 11Note que os elementos infinitesimais de deslocamento , e , de acordo com a expressão (2.33), são a forma abreviada de , e e que a primitiva é igual à primitiva .
onde e são as distâncias desde os pontos P e Q até à carga pontual (figura 2.15).
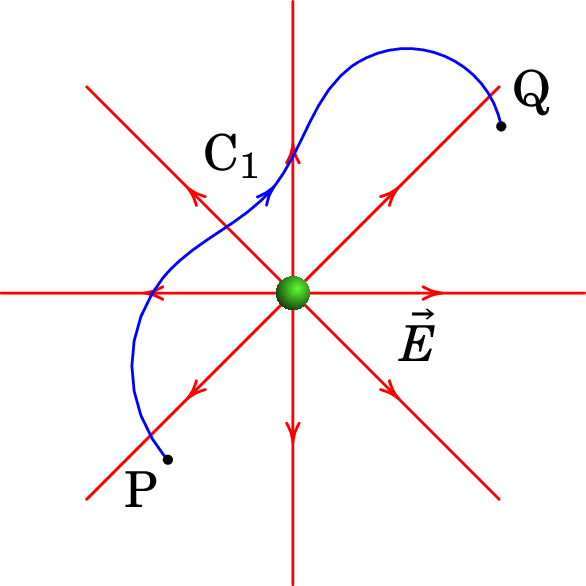
Este resultado não depende da curva , mas somente da posição dos pontos inicial e final dessa curva. Como tal, o integral conduz ao mesmo resultado nas curvas e na figura 2.14 ou em qualquer outra curva entre P e Q.
O campo de uma distribuição de cargas mais complexa é a soma dos campos de várias cargas pontuais. Cada integral de linha 2.14 é então a soma de vários integrais para cada uma dessas cargas pontuais e o resultado final depende apenas das posições dos pontos P e Q mas não da curva entre eles. Fica assim demonstrado que o campo elétrico produzido por qualquer distribuição de carga é um campo conservativo.
De salientar que o facto do campo elétrico ser conservativo é uma consequência direta do campo elétrico produzido por uma carga pontual ser um campo radial esférico, i.e, .
Tal como mostra a figura 2.16, qualquer curva fechada C pode ser dividida em duas curvas abertas, e , entre dois pontos P e Q na curva C. Como tal, o integral de linha do campo elétrico, ao longo duma curva fechada C, pode sempre ser escrito como a soma de dois integrais de linha, um desde um ponto P até outro ponto Q, ao longo duma curva , e o outro desde Q até P, ao longo de outra curva .
| (2.35) |
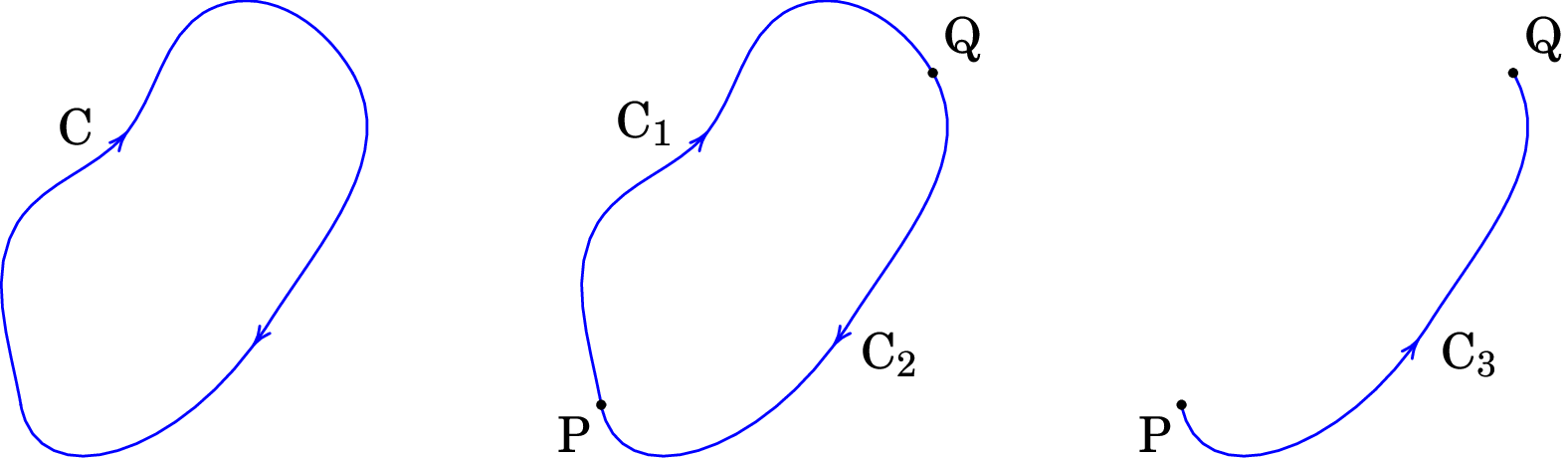
Invertendo o sentido da curva , obtém-se a curva apresentada no lado direito da figura 2.16, que vai desde o ponto P até o ponto Q. Como os pontos por onde passam as duas curvas e são os mesmos mas o sentido é oposto, os integrais de linha de qualquer campo vetorial, em particular do campo , ao longo dessas duas curvas são iguais mas de sinal oposto:
| (2.36) |
e o integral ao longo da curva fechada C é então dado por:
| (2.37) |
Os dois integrais no lado direito da equação anterior são ambos desde o ponto P até o ponto Q, mas ao longo de duas curvas diferentes entre esses pontos. Como o integral de linha do campo elétrico não depende do percurso usado entre esses pontos, conclui-se que o integral de linha em qualquer curva fechada é nulo:
| (2.38) |
Se o integral de linha de é nula em qualquer curva fechada C, a expressão (A.78) do apêndice A implica que o rotacional do campo elétrico é nulo em qualquer ponto do espaço:
| (2.39) |
O rotacional é outro campo vetorial, com 3 componentes. Em coordenadas cartesianas, igualando a zero cada uma das três componentes cartesianas do rotacional de (equação (A.76)), obtêm-se as seguintes 3 equações escalares:
As quatro equações (2.31), (2.38), (2.39) e (2.40) são equivalentes e permitem conferir que um campo é conservativo. A equação (2.40) indica que as derivadas cruzadas das componentes cartesianas do campo elétrico deverão ser iguais: a derivada de , em ordem a , deverá ser igual à derivada de , em ordem a , e de forma semelhante para qualquer outro par de coordenadas.
No capítulo 9, sobre indução eletromagnética, veremos que para além das cargas elétricas, outra possível fonte do campo elétrico é um campo magnético variável no tempo. O campo elétrico que temos considerado até agora, produzido por cargas, é designado de campo eletrostático e é conservativo. O campo elétrico induzido por campos magnéticos variáveis no tempo não é eletrostático e não é conservativo.
Numa região do espaço onde a densidade de carga é conhecida, as equações (2.30) e (2.39), juntamente com condições apropriadas para o valor do campo elétrico na fronteira dessa região, permitem calcular o campo elétrico em todos os pontos da região. Quando a região em causa é todo o espaço, a fronteira da região situa-se no infinito. A condição na fronteira é que o campo deverá aproximar-se de zero quando a distância às partes onde existe carga se aproximar de infinito. Existem vários métodos diferentes para resolver essas equações, que estão para além dos objetivos deste livro introdutório.
Problemas
-
2.1.
Uma pequena esfera com massa igual a 25 g e carga de 50 nC encontra-se pendurada de um fio isolador de 7 cm que está colado a um plano vertical. O plano vertical tem densidade superficial de carga constante, nC/cm, e pode ser considerado infinito. Calcule o ângulo que o fio faz com o plano vertical.

-
2.2.
Numa região do espaço há três cargas pontuais, µC no ponto (em cm), µC em e µC em . Calcule o fluxo elétrico através de uma superfície esférica de raio 3 cm, com centro no ponto (1, 0, 0).
-
2.3.
Na atmosfera existe um campo elétrico, o qual aponta na vertical para baixo. Ao nível do mar, o módulo do campo é aproximadamente 120 N/C e diminui em função da altura; 2 km acima do nível do mar o campo é aproximadamente 66 N/C. Que pode concluir acerca do sinal das cargas livres nos dois primeiros quilómetros da atmosfera? Calcule a densidade volúmica de carga média nessa região.
-
2.4.
Uma carga pontual de 5 nC encontra-se a 6 cm de um fio retilíneo muito comprido, com densidade linear de carga constante, igual a 7 nC/cm. Calcule a força elétrica da carga sobre o fio (sugestão: calcule a força do fio sobre a carga pontual, que é mais fácil de calcular, a qual, pela lei de ação e reação, possui o mesmo módulo da força da carga sobre o fio).
-
2.5.
Um fio não-condutor no plano , forma uma circunferência de raio com centro na origem. O fio tem densidade linear de carga não-uniforme , onde é o ângulo em coordenadas polares, cuja origem é o centro da circunferência. Calcule o campo elétrico na origem.
-
2.6.
Um protão passa pela origem, em , com velocidade Mm/s, dentro de uma região onde há vácuo e campo elétrico uniforme, . Determine o valor que deverá ter para que o protão atravesse o eixo dos em cm. (O peso do protão pode ser desprezado neste caso).
-
2.7.
Calcule a carga total dentro do paralelepípedo: cm, cm, cm, onde o campo elétrico é (unidades SI).
-
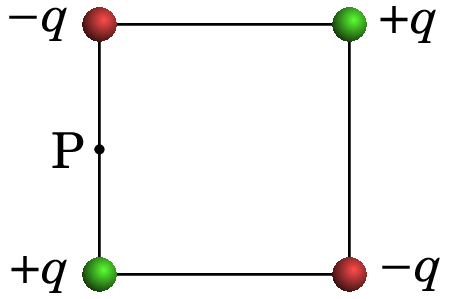
2.8.
Quatro cargas com valores e (), encontram-se nos vértices dum quadrado de aresta . Determine a expressão do campo elétrico , no ponto P (no meio da aresta do lado esquerdo), em função de , e da constante de Coulomb .
-
2.9.
Usando o resultado do Exemplo 2.3 para o campo de um disco plano, calcule o campo elétrico produzido por um plano infinito, com densidade superficial de carga constante.
-
2.10.
Um disco de 8 cm de raio, tem densidade superficial de carga , onde é a distância desde o centro, e uma constante igual a 4 C/m. Calcule a carga total do disco, e o campo elétrico ao longo do seu eixo longitudinal.
-
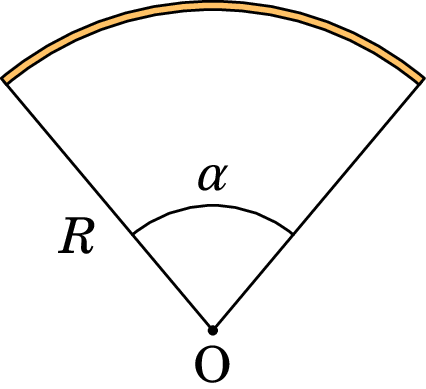
2.11.
Um fio fino tem densidade linear de carga constante e forma um arco circular que subtende um ângulo de , conforme indicado na figura. Mostre que a expressão do módulo do campo elétrico no ponto O é:
-
2.12.
Um fio retilíneo tem densidade linear de carga constante. Determine a expressão do campo elétrico em qualquer ponto P em função da distância ao fio, , e dos ângulos e definidos na figura. Calcule o valor limite do campo quando o fio for infinito. (Sugestão: defina o eixo na direção do fio e o eixo desde o fio até o ponto P.)
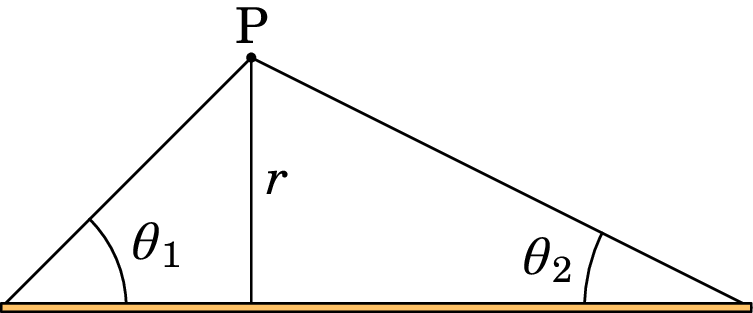
Nota: e .
-
2.13.
O campo elétrico numa dada região do espaço é dado em coordenadas esféricas por:
Calcule a carga total dentro de uma esfera de 6 cm de raio e centro na origem. (As distâncias são dadas em cm e o campo em N/C.)
-
2.14.
Considere o protão como uma pequena esfera sólida de raio m, com carga distribuída uniformemente no seu interior. Calcule o campo elétrico na sua superfície e num ponto a m do centro.
-
2.15.
A figura representa o corte transversal de um cilindro sólido, muito comprido, de raio cm e densidade volúmica de carga constante nC/m e com uma cavidade cilíndrica de raio cm. Calcule o campo elétrico no ponto P.
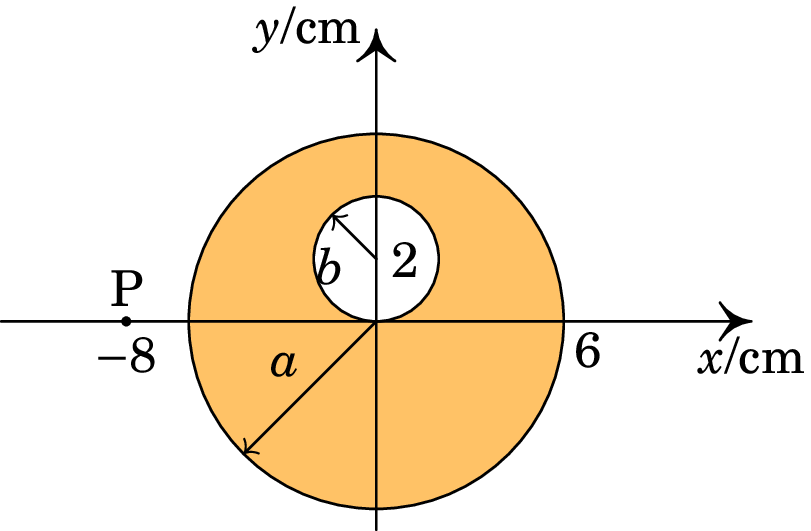
Sugestão: para calcular o campo, usando a lei de Gauss, é possível considerar o sistema como a sobreposição de um cilindro infinito maciço, de raio e centro na origem, com densidade volúmica de carga (parte (a) da figura abaixo) e um cilindro também infinito, de raio e centro no ponto , com densidade volúmica de carga (parte (b) da figura abaixo).
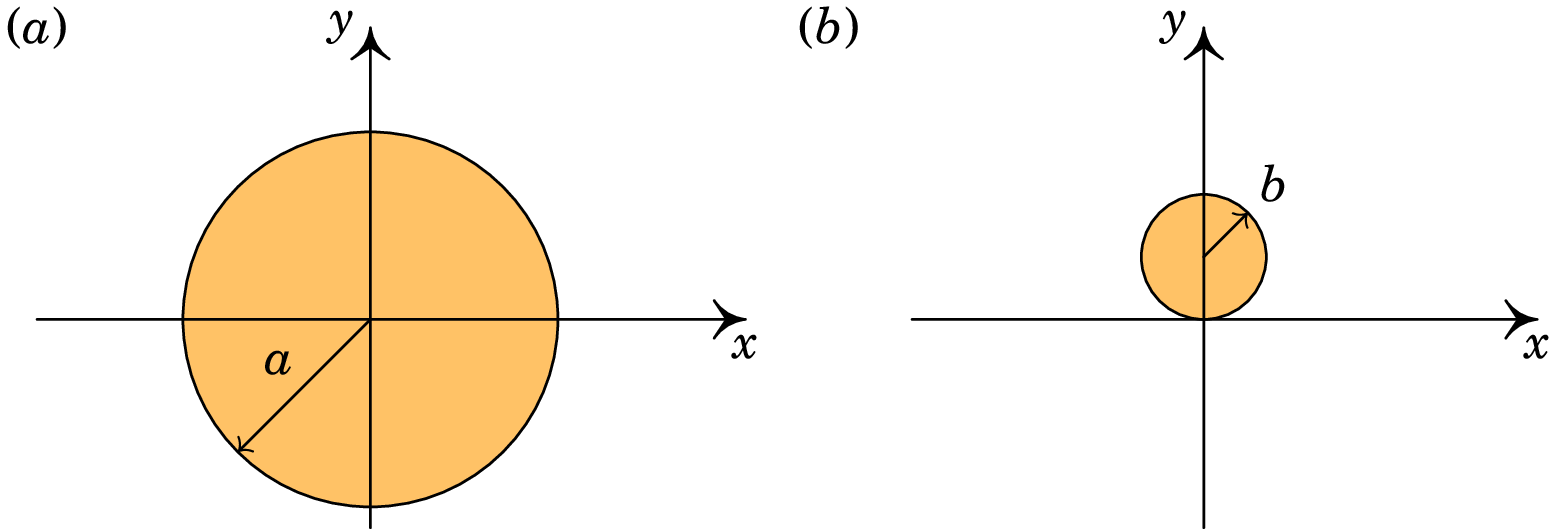
-
2.16.
Calcule o campo elétrico produzido pela densidade volúmica de carga dada pela seguinte expressão (em unidades SI), a qual possui simetria esférica, sendo a distância ao ponto de simetria:
-
2.17.
No átomo de hidrogénio, o eletrão encontra-se em movimento muito rápido à volta do núcleo. O resultado médio no tempo é uma distribuição contínua de carga (nuvem eletrónica) com densidade volúmica de carga
onde é a carga elementar, uma constante aproximadamente igual a , e a distância desde o núcleo. Considere que a nuvem eletrónica se estende até ao infinito.
(a) Mostre que a carga total da nuvem eletrónica é igual à carga do eletrão, .
Nota: .
(b) Calcule o campo elétrico produzido pela nuvem eletrónica.
(c) Calcule o campo total do átomo de hidrogénio. (Sugestão: o campo do núcleo é igual ao campo de uma partícula pontual de carga , na origem.) -
2.18.
Uma esfera de raio , tem uma carga total distribuída de tal forma que a densidade volúmica de carga é , onde é uma constante e a distância ao centro da esfera.
(a) Calcule o valor da constante em função da carga .
(b) Calcule o campo elétrico no interior e no exterior da esfera, e faça o gráfico do módulo do campo em função de . -
2.19.
A densidade volúmica de carga no interior de um cilindro muito comprido de raio é
onde é a distância ao eixo do cilindro e é uma constante. Calcule o campo elétrico em qualquer ponto do espaço, em função dos parâmetros , e .
Respostas
-
2.1.
°.
-
2.2.
-
2.3.
São positivas. A densidade volúmica de carga é .
-
2.4.
1.05 mN.
-
2.5.
.
-
2.6.
N/C.
-
2.7.
pC.
-
2.8.
-
2.9.
, perpendicular ao plano.
-
2.10.
257 pC. ( em cm e em N/C).
-
2.12.
O campo do fio infinito é: .
-
2.13.
1545 nC.
-
2.14.
N/C e N/C.
-
2.15.
N/C.
-
2.16.
( em m, em N/C).
-
2.17.
(b) .
(c) . -
2.18.
(a) .
(b) -
2.19.
O campo é na direção perpendicular ao eixo do cilindro e com valor: