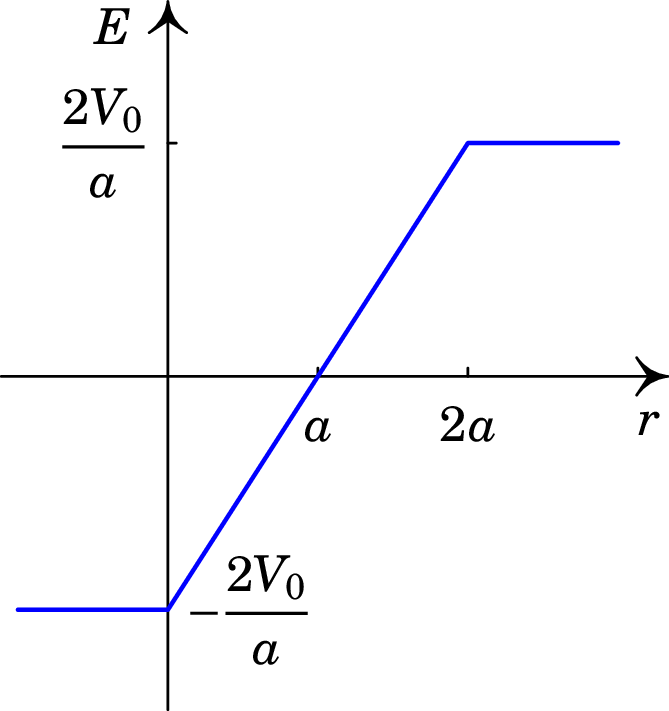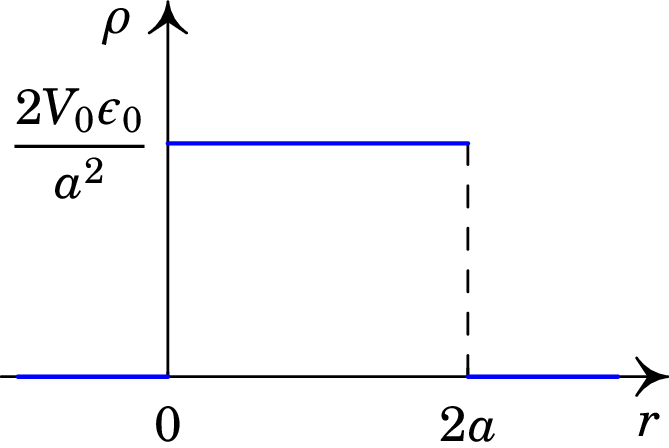3. Potencial eletrostático

Henry Cavendish (1731–1810)
Cavendish descobriu que quando dois condutores são ligados por um fio condutor ficam com o mesmo “grau de eletrificação”, o que hoje em dia designamos por potencial elétrico. Por meio de experiências Cavendish obteve a relação entre as cargas de uma esfera condutora e de um disco condutor, plano, quando colocados em contacto por meio de um fio condutor. Resultado esse que só foi publicado 100 anos mais tarde, em 1879, quando Lord Kelvin o encontrou nos manuscritos de Cavendish. De facto, Cavendish fez muitas descobertas anos antes de serem redescobertas por outros investigadores, mas não chegou a publicar os seus resultados. Um desses resultados foi a Lei de Coulomb, anos antes da publicação de Coulomb em 1784.
3.1 Diferença de potencial eletrostático
No capítulo anterior, a demonstração de que o campo elétrico é conservativo foi feita mostrando que o integral de linha do campo de uma carga pontual em qualquer curva C entre dois pontos P e Q, depende apenas das distâncias de P e Q até à carga e não da curva C escolhida (equação (2.34)):
| (3.1) |
A um campo vetorial conservativo está sempre associado um campo escalar. No caso do campo elétrico, o campo escalar associado denomina-se por potencial elétrico. Define-se o potencial elétrico devido a uma carga pontual na origem como:
| (3.2) |
e a equação (3.1) diz simplesmente que o integral de linha do campo entre dois pontos P e Q, é igual ao potencial no ponto inicial menos o potencial no ponto final, independentemente do percurso de integração.
O potencial tem unidades de campo elétrico vezes uma distância, o que é igual a força vezes uma distância a dividir por carga. A unidade SI de potencial elétrico é o volt (V), em homenagem ao físico italiano Alessandro Volta:
| (3.3) |
onde J (joule) é a unidade SI de energia.
Observe-se que na definição (3.2) do potencial da carga pontual podíamos ter somado qualquer constante arbitrária, sem contrariar a equação (3.1), mas habitualmente define-se de forma a que seja nulo no limite . Do ponto de vista físico, o valor do potencial num qualquer ponto P está definido a menos de uma constante arbitrária. O que tem significado físico, i.e., o que pode ser medido no laboratório é a diferença de potencial entre dois pontos P e Q.
Em geral, o integral de linha de qualquer campo eletrostático entre um ponto inicial P e um ponto final Q é a diferença do valor de uma função escalar entre os pontos P e Q. O integral de linha do campo pode então ser usado para definir a diferença de potencial eletrostático associada a um qualquer campo eletrostático:
| (3.4) |
O potencial num ponto P, arbitrando potencial nulo no infinito, , é então igual a:
| (3.5) |
Assim, quando nos referirmos ao potencial num ponto à distância de uma carga pontual, estaremos então a referir-nos implicitamente à diferença de potencial entre esse ponto e o infinito:
| (3.6) |
Em sistemas hipotéticos — plano infinito com carga, cabo infinito com carga, etc. — o integral na equação anterior diverge porque o módulo do campo não se aproxima de zero no infinito. Nesses casos arbitra-se que é zero em algum ponto (e.g., o próprio plano ou na superfície do cabo infinito) e o limite superior do integral em (3.5) será esse ponto.
Ao contrário do campo elétrico, o qual pode apresentar descontinuidades, o potencial eletrostático é sempre dado por uma função contínua. A continuidade do potencial eletrostático decorre da sua própria definição: considerando a expressão (3.4), vemos que no limite em que o ponto tende para o ponto , então .
Exemplo 3.1
O campo elétrico numa região do espaço é dado pela expressão
(a) Mostre que o campo é conservativo.
(b) Calcule o potencial nessa região.
Resolução. (a) Basta conferir que as derivadas cruzadas das três componentes cartesianas do campo são iguais:
(b) Como a expressão dada para o campo não se aproxima de zero no infinito, vamos arbitrar que o potencial seja nulo na origem: . O potencial num ponto qualquer é então igual a menos o integral de linha do campo, desde a origem até o ponto P:
Como o campo elétrico é conservativo, o percurso de integração pode ser um qualquer entre O e P. Usaremos a linha reta entre esses pontos, descrita pela seguinte equação paramétrica:
onde é o vetor posição de P, enquanto que é o vetor posição dos pontos da reta, em função do parâmetro , o qual varia entre 0 e 1. A expressão do campo elétrico ao longo da reta entre O e P é:
E o integral de linha é:
O potencial é então a função:
3.2 Relação entre potencial e campo elétrico
O potencial é uma função que a cada ponto do espaço associa um valor numérico, isto é, o potencial é um campo escalar. Por exemplo, em coordenadas cartesianas, o potencial é dado pela função . Por outro lado, o campo elétrico é um campo vetorial, ou seja, é uma função vetorial que a cada ponto do espaço associa um vetor, a saber, . Particularizando, em coordenadas cartesianas, o campo elétrico é escrito como . Como o vetor campo elétrico possui três componentes, o campo elétrico é definido por três funções.
Uma vez que o potencial é definido a partir do campo elétrico, expressão (3.4), deverá ser possível obter o campo a partir do potencial, o que permitiria obter as três componentes do campo a partir de uma única função.
Para mostrar como obter o campo elétrico a partir do potencial usaremos o conceito de derivada direcional de uma função de várias variáveis (ver expressão (A.68)), em particular do potencial que depende de 3 variáveis. A derivada direcional do potencial num ponto P de vetor posição , na direção de um versor , é o limite (ver figura 3.1):
| (3.7) |
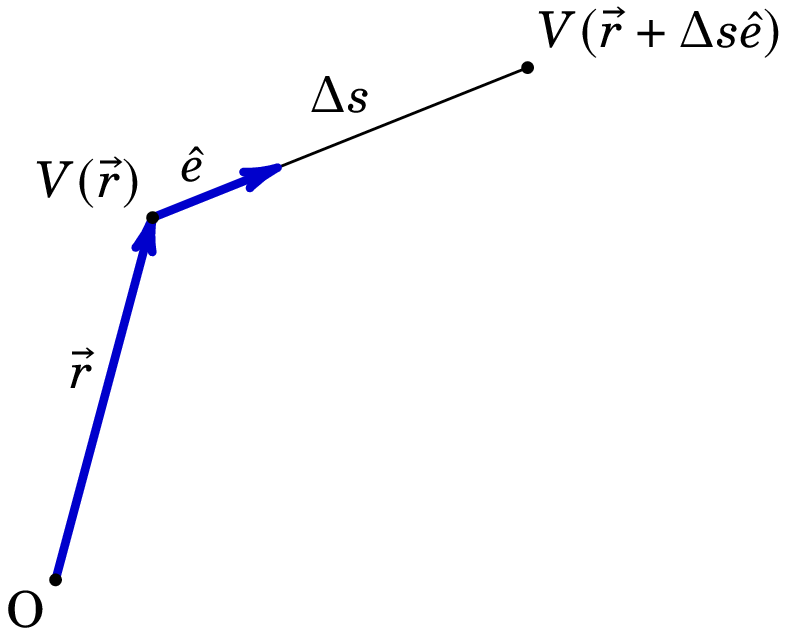
De acordo com a expressão (3.4), a diferença de potencial no numerador da equação (3.7) é igual a menos o integral de linha do campo elétrico desde o ponto P com vetor posição até ao ponto Q com vetor posição . No limite , o ponto Q aproxima-se de P, e o integral é igual a menos o produto do campo elétrico em P pelo deslocamento desde P até Q:
| (3.8) |
Assim, a derivada direcional do potencial na direção de um versor, expressão (3.7), é então igual a menos o produto escalar do campo vezes o versor
| (3.9) |
Em coordenadas cartesianas, as derivadas de nas direções dos versores , e são as três derivadas parciais do potencial, o que de acordo com a equação anterior são
| (3.10) |
e a expressão do campo elétrico em qualquer ponto do espaço é
| (3.11) |
Usando o operador nabla (A.82), temos que:
| (3.12) |
onde é o gradiente do potencial. A equação (3.12) é geral para qualquer campo eletrostático. Enquanto que a equação (3.11) mostra as três componentes do gradiente em coordenadas cartesianas, a sub-secção A.3.1 do apêndice A mostra como são as componentes do gradiente em outros sistemas de coordenadas. Combinando as equações (3.9) e (3.12), obtém-se
| (3.13) |
que é a expressão geral (A.68) do apêndice A para qualquer campo escalar. Como o potencial elétrico se obtém por integração do campo elétrico, ver expressões (3.4) ou (3.5), intuitivamente, é de esperar que o campo elétrico se obtenha por derivação do potencial elétrico, conforme expressão (3.12). No caso de uma carga pontual na origem, a seguinte identidade (ver problema 3.1 no fim do capítulo)
| (3.14) |
mostra que a expressão do campo elétrico obtida no capítulo 1 (1.12) é de facto igual a menos o gradiente da expressão do potencial (3.2) – verifique!
O valor máximo do produto escalar é igual ao módulo do campo elétrico e obtém-se quando o versor estiver na mesma direção e sentido do campo elétrico. Como tal, a equação (3.9) implica que o campo elétrico aponta sempre na direção e sentido em que o potencial diminui mais rapidamente.
As linhas de campo elétrico estão sempre orientadas desde pontos de maior potencial para pontos de menor potencial. Uma vez que uma linha de campo passe por um ponto a um determinado potencial, não pode voltar a passar por pontos com potencial igual ou superior. Consequentemente, as linhas de campo eletrostático nunca podem ser fechadas, i.e., são sempre abertas.
3.3 Potencial de sistemas de cargas pontuais
Tal como foi dito no capítulo 2 o campo elétrico de um sistema de cargas pontuais , , …, é igual à soma vetorial dos campos produzidos individualmente por cada carga. A equação (3.5) implica que o potencial produzido pelas cargas pontuais será a soma dos potenciais de cada carga individual.
A expressão (3.2) para uma carga pontual é válida unicamente se a carga estiver na origem. Com cargas em pontos diferentes já não é possível que estejam toda na origem; se a carga estiver no ponto de vetor posição , a distância na equação (3.2) deverá ser substituída pela distância entre os pontos com vetores de posição e :
| (3.15) |
E o potencial das cargas é
| (3.16) |
A identidade (3.14) pode ser escrita substituindo por :
| (3.17) |
que mostra a relação entre as expressões para o potencial (3.16) e o campo elétrico (2.4) de um sistema de cargas pontuais.
A expressão do potencial elétrico (3.16), a qual envolve uma soma escalar, é mais simples de usar do que a expressão do campo elétrico, uma vez que esta envolve uma soma vetorial.
Exemplo 3.2
Uma carga pontual de nC encontra-se no ponto (coordenadas em cm) e uma segunda carga pontual de +4 nC encontra-se no ponto . (a) Calcule o potencial no ponto de coordenadas . (b) Encontre a expressão para o potencial em qualquer ponto .
Resolução. Com cargas em nC e distâncias em cm, a constante de Coulomb é:
(a) As distâncias desde até as duas cargas são
e o potencial no ponto é
(b) Substituindo as expressões para as distâncias entre as cargas e o ponto de coordenadas , obtém-se (coordenadas em cm e potencial em V):
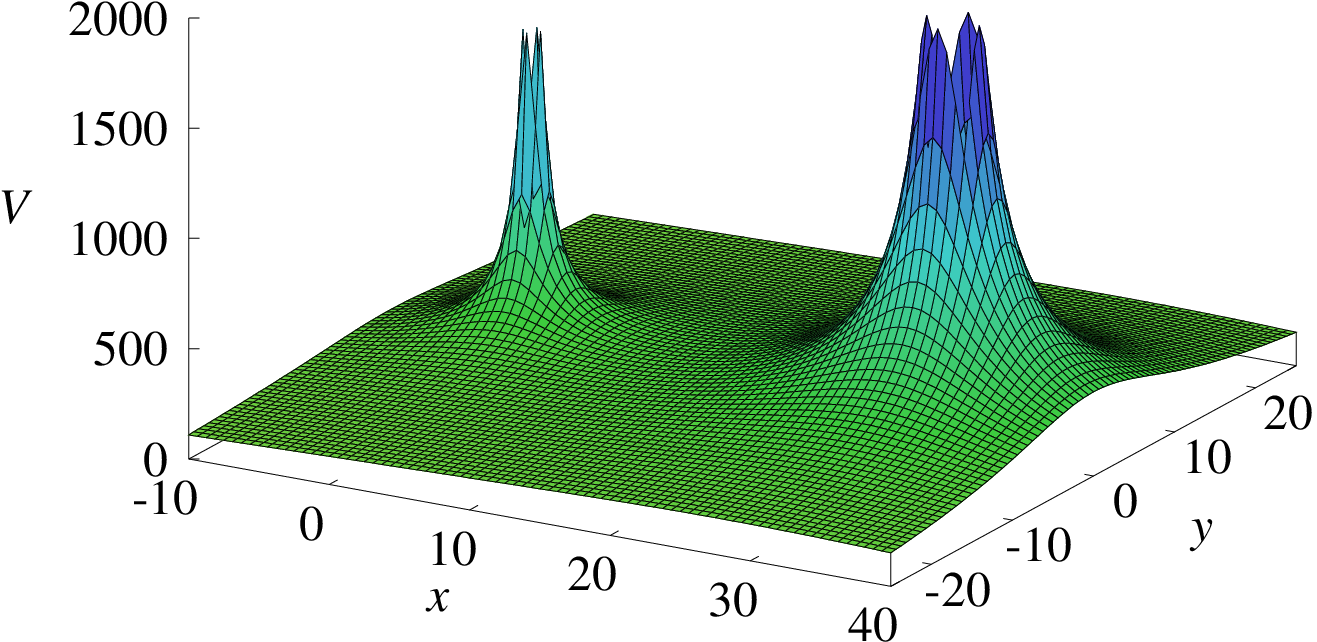
No exemplo 3.2 o sistema é invariante em relação a rotações em torno da reta que passa pelas duas cargas. Como foi dito no capítulo 1, bastaria representar as linhas de campo num plano contendo essa reta. A distância entre as duas cargas é de 30 cm; deslocando e rodando o sistema de coordenadas de forma a que a primeira carga fique na origem e a segunda carga no eixo no ponto , bastaria representar as linhas de campo no plano , para o qual . Consequentemente, é suficiente representar o potencial no plano com a primeira carga na origem e a segunda carga em :
| (3.18) |
Esta função de duas variáveis pode ser representada graficamente tal como mostra a figura 3.2. Nos pontos onde se encontram as cargas pontuais positivas o potencial aproxima-se de ; no entanto, nesses pontos o campo não é infinito, mas é igual ao campo produzido apenas pela carga que não está no respetivo ponto.
3.4 Superfícies equipotenciais
Os pontos do espaço nos quais o potencial tem o mesmo valor formam uma superfície contínua chamada superfície equipotencial. Em cada ponto do espaço, o potencial tem um único valor e se o campo elétrico é diferente de zero nesse ponto, então existe uma única superfície equipotencial que passa por esse ponto.
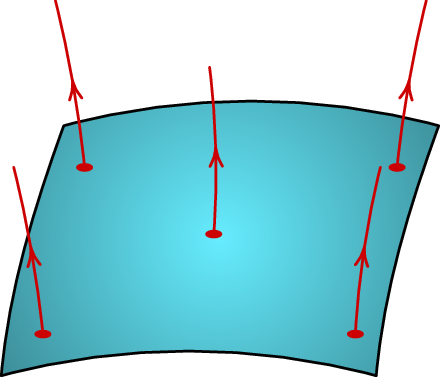
A figura 3.3 mostra uma parte de uma superfície equipotencial. A derivada direcional do potencial em qualquer direção tangente a esse superfície é nula, já que o potencial é constante sobre a superfície. Como tal, a equação (3.9) , ou seja o campo elétrico é perpendicular à superfície equipotencial:
As superfícies equipotenciais são as superfícies perpendiculares às linhas de campo elétrico e o sentido das linhas de campo indicam a direção em que o potencial diminui.
As cinco linhas de campo apresentadas na figura 3.3 são todas perpendiculares a ela e o seu sentido indica que por cima dessa superfície equipotencial o potencial será menor e debaixo será maior.
Na representação do potencial num plano, as superfícies equipotenciais aparecem como curvas, que correspondem à interseção das superfícies equipotenciais com o plano. Por exemplo a figura 3.4 mostra, em azul, as curvas equipotenciais do potencial (3.18) de duas cargas de nC e nC afastadas 30 cm. As linhas de campo elétrico também são apresentadas, a vermelho.
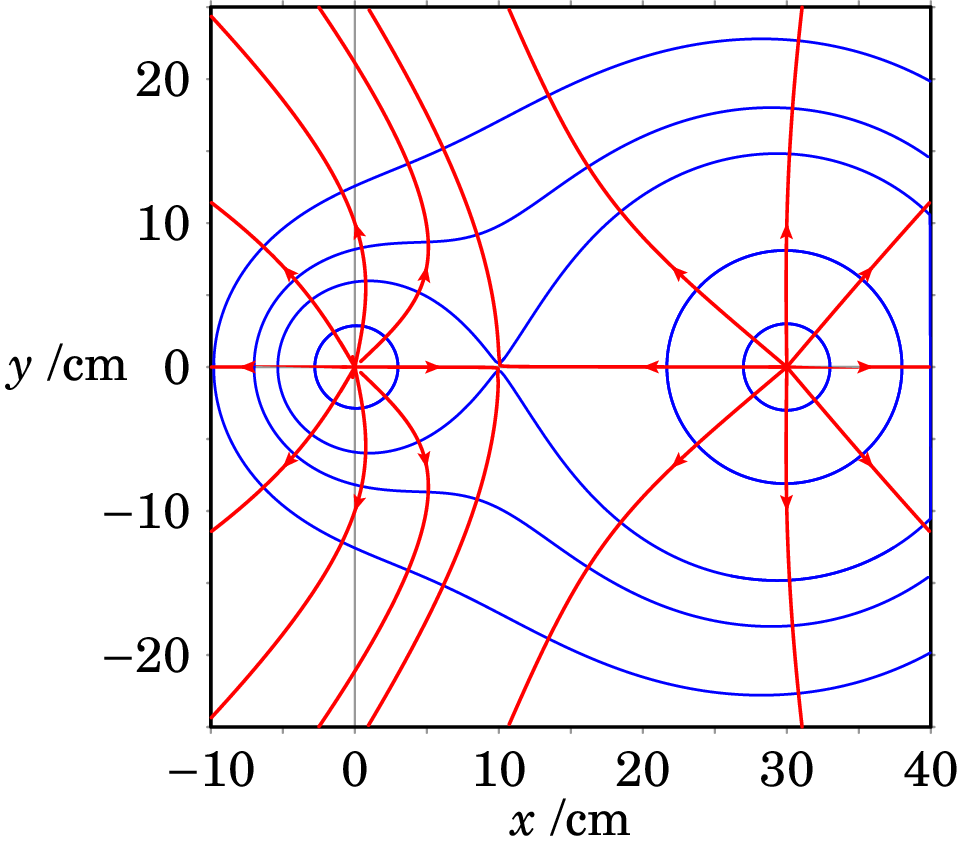
Na origem e no ponto na figura 3.4, onde há cargas pontuais positivas, as linhas de campo divergem em todas as direções, o fluxo elétrico numa pequena superfície fechada à volta de um desses pontos é positivo, o potencial aproxima-se de e esse dois pontos são máximos do potencial. O ponto é um ponto de sela do potencial, o campo é nulo neste ponto e nele o número de linhas de campo que convergem tem de ser igual ao número de linhas de campo que divergem. A curva equipotencial que passa pelo ponto de sela cruza-se consigo própria nesse mesmo ponto. Em três dimensões a respetiva superfície equipotencial é como a superfície de duas gotas que se tocam nesse ponto.
Nos pontos onde há cargas pontuais negativas o potencial aproxima-se de , esses pontos são mínimos do potencial e há linhas de campo a convergirem nesses pontos desde todas as direções.
No caso de cargas distribuídas continuamente numa região, o potencial não se aproxima de nessas regiões, mas terá máximos locais nas regiões com carga positiva e mínimos locais nas regiões com carga negativa.
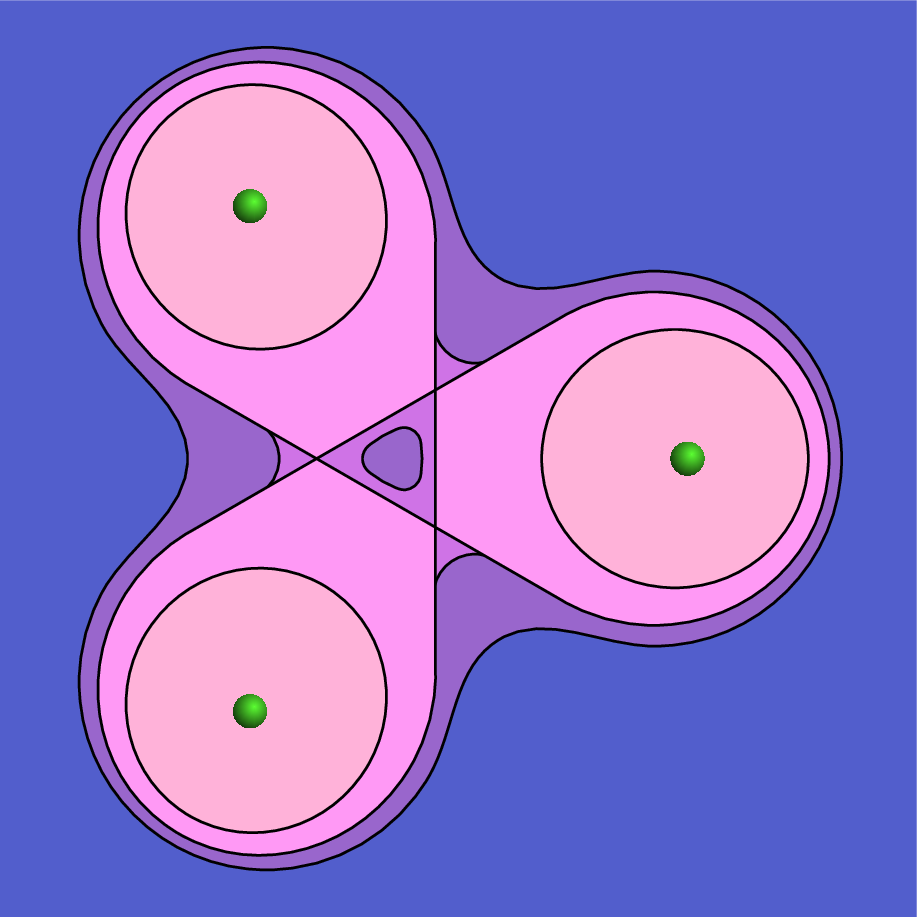
A figura 3.5 mostra outro exemplo, o potencial de um sistema de três cargas pontuais positivas e iguais, localizadas nos vértices de um triângulo equilátero. Existem quatro pontos de sela onde o campo elétrico é nulo; três desses pontos são os vértices do triângulo no centro da figura, onde há cruzamento de linhas equipotenciais. O quarto ponto é o ponto equidistante às três cargas, onde também existe interseção de duas superfícies equipotenciais (como as duas superfícies se cruzam em direções fora do plano da figura não aparecem na figura). Sobre o plano da figura o potencial diminui na direção desse quarto ponto de sela, mas nas direções perpendiculares à figura o potencial aumenta.
Podem também existir regiões do espaço onde o campo é nulo, sendo o potencial constante em toda a região. Nesse caso temos um volume equipotencial; um exemplo é o volume ocupado por um condutor em equilíbrio eletrostático.
Exemplo 3.3
Encontre o campo elétrico e as superfícies equipotenciais correspondentes ao potencial (unidades SI).
Resolução. O campo elétrico é menos o gradiente do potencial:
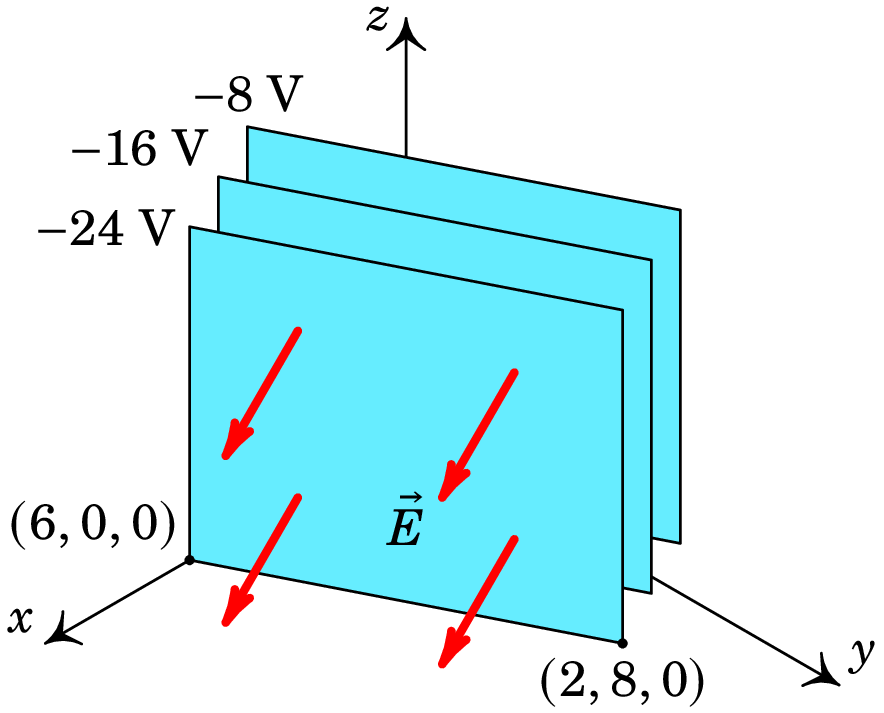
O campo é um vetor constante, i.e., é um campo uniforme. Cada superfície equipotencial é um plano de equação:
com um valor dado de V. Em particular, as equipotenciais de V, V e V são os três planos definidos pelas seguintes equações:
A figura seguinte mostra os três planos equipotenciais e o campo elétrico em quatro pontos. Observe-se que o campo elétrico é perpendicular aos planos equipotenciais e aponta no sentido em que o potencial diminui.
3.5 Potencial de distribuições contínuas de carga
Para calcular o potencial produzido por uma distribuição procede-se de forma semelhante ao cálculo do campo elétrico na secção 2.2, dividindo a região onde ha carga em sub-regiões (), cada uma com carga suficientemente pequena para que possa ser considerada como uma carga pontual. Seja a carga de cada sub-região tal que . Seja também o vetor posição de cada uma dessas sub-regiões .
O potencial num ponto P de vetor posição é dado, aproximadamente, pela expressão (3.16) para um sistema de cargas pontuais:
| (3.19) |
onde é o modulo do vetor desde a região até o ponto P, ou seja, a distância desde a região até P (ver figura 2.2 no capítulo 2).
A aproximação torna-se exata no limite . Neste limite, a carga de cada região torna-se num elemento infinitesimal de carga , igual à densidade volúmica de carga, , vezes o elemento infinitesimal de volume, , os vetores posição tornam-se num contínuo de vetores posição identificando todos os pontos da região R carregada e o somatório torna-se num integral de volume sobre toda a região com carga:
| (3.20) |
onde varia dentro da região R de integração.
Se a carga estiver distribuída sobre uma superfície, o potencial será um integral de superfície:
| (3.21) |
Finalmente, se a carga estiver distribuída sobre uma linha, o potencial é calculado através de um integral de linha:
| (3.22) |
Os integrais que definem o potencial são semelhantes aos integrais usados para calcular o campo (capítulo 2). No entanto, para se determinar o potencial elétrico é preciso calcular apenas um integral e não três integrais (um para cada uma das três componentes) como no caso do cálculo do campo elétrico.
Como veremos nos dois exemplos a seguir, para determinar o campo elétrico de distribuições de carga, costuma ser mais fácil encontrar primeiro o potencial por integração e calcular o seu gradiente para obter o campo elétrico. No entanto, nos sistemas com algum simetria será mais fácil usar o processo posto, i.e., determinar o campo a partir da lei de Gauss e integrá-lo para obter o potencial.
Exemplo 3.4
Calcule o potencial e o campo elétrico devidos a uma esfera condutora de raio , com carga .
Resolução. Como a esfera é condutora, a carga distribuir-se-á uniformemente na sua superfície. Embora exista simetria esférica, sendo muito fácil obter o campo a partir da lei de Gauss, vamos calcular o potencial a partir do integral duplo (3.21), para ilustrar este método.
A densidade superficial de carga na superfície da esfera é constante e dada por:
Escolhendo a origem no centro da esfera, o eixo na direção do ponto P onde se pretende calcular o potencial e usando coordenadas esféricas, o vetor posição de P é , o vetor posição da carga é pelo que
com módulo:
Como na superfície da esfera é constante, usa-se o elemento infinitesimal de área da equação (A.60) para integrar a equação (3.21)
O integral em é igual a e o resultado do integral em conduz a
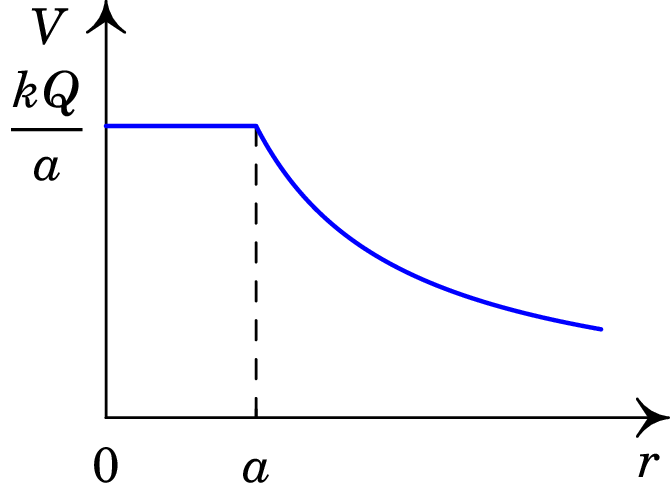
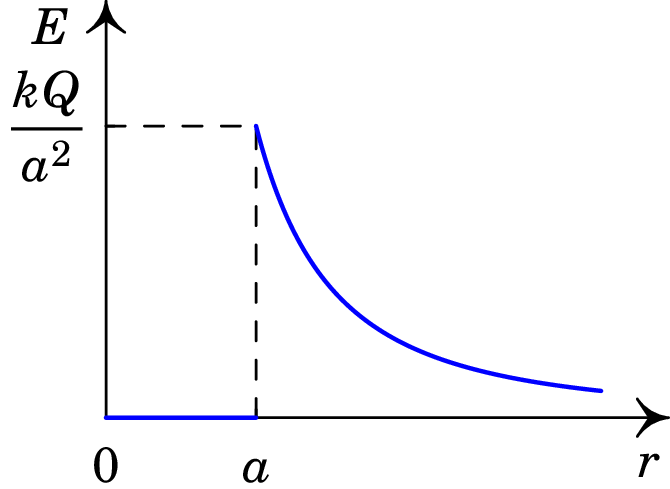
No interior da esfera (), , e:
Fora da esfera (), , e o potencial é
No interior da esfera, como o potencial é constante, o campo elétrico é nulo. No exterior da esfera, usando a expressão do gradiente em coordenadas esféricas (equação (A.70)), obtém-se a componente radial do campo:
O resultado do exemplo anterior, que será usado nos próximos capítulos, é fácil de lembrar, já que em o potencial e o campo são iguais aos de uma carga pontual concentrada no centro da esfera. Em , o campo é nulo e o potencial é constante, com o mesmo valor que possui na sua superfície. Em o potencial é contínuo, enquanto que o campo elétrico é descontínuo devido à aproximação de considerar a carga concentrada numa superfície sem nenhuma espessura. Na realidade a carga distribui-se numa camada muito fina na superfície, onde o campo varia continuamente desde zero até .
Resumindo, a expressão do potencial devido a uma esfera condutora de raio com carga é:
| (3.23) |
onde é a distância desde o centro da esfera. O campo elétrico é na direção radial, com componente radial dada por:
| (3.24) |
A figura 3.6 mostra os gráficos do potencial e da intensidade do campo elétrico.
 |
 |
Exemplo 3.5
Calcule o potencial produzido por um cilindro infinito, de raio R, com densidade volúmica de carga constante.
Resolução. Neste caso calcularemos primeiro o campo elétrico e a partir dele o potencial. Como existe simetria cilíndrica, o campo é na direção radial cilíndrica e com componente radial cilíndrica dada pela expressão (2.27) do capítulo 2
onde é a distância até o eixo do cilindro, e a carga dentro de uma superfície cilíndrica de raio e altura , com eixo no eixo de simetria. Usando a expressão (A.51) do elemento infinitesimal de volume em coordenadas cilíndricas, a carga dentro dessa superfície é
Se , é constante em todo o intervalo de integração, e o resultado do integral em é . Já se , é nula entre e e o resultado do integral é . Como tal, a carga interna é:
E a componente radial cilíndrica do campo é
Note que o campo elétrico é contínuo na superfície do cilindro, pois .
Neste sistema não é possível arbitrar potencial nulo no infinito. Podemos então arbitrar em que conduz a integrais mais simples e o percurso de integração será na direção radial cilíndrica, desde até . Se , em todo percurso de integração a expressão do campo é e o potencial é:
Em ,
Note que o potencial elétrico também é contínuo, como deve ser sempre, na superfície do cilindro, pois .
No exemplo anterior, se tivéssemos escolhido noutro valor diferente de , o resultado para seria o mesmo que obtivemos, mais um termo constante. No cálculo de integrais de funções definidas com expressões diferentes em diferentes intervalos, é preciso ter em conta que o intervalo de integração poderá ter de ser dividido em subintervalos, correspondentes às diferentes expressões da função. No exemplo anterior isso foi evitado escolhendo o valor de referência exatamente em , que é onde a expressão de se altera.
3.6 Expansão multipolar do potencial
Nesta secção encontraremos uma expressão para o potencial devido a uma carga distribuída dentro de uma região do espaço em pontos muito afastados da região onde a carga é não nula. Se a carga total dentro da região for diferente de zero, vimos no capítulo 1 que a distâncias muito maiores do que as dimensões lineares da região onde a carga é não nula, as linhas de campo deverão ter simetria radial esférica e o potencial aproximar-se-á do potencial de uma carga pontual, sendo a sua carga igual à carga total dentro da região. Mas como será no caso em que a carga total dentro da região é nula? Como serão o potencial e o campo elétrico de uma molécula, cuja carga total é nula?
É conveniente definir os vetores posição e na expressão (3.20) do potencial em relação a uma origem dentro da região R onde há carga, tal como mostra a figura 3.7.

Para encontrar a expressão do potencial em pontos muito afastados da região R, teremos de calcular o integral em (3.20) no limite em que for muito maior do que , i.e., . Observe-se que
| (3.25) |
e os dois primeiros termos na série de potências em são:
| (3.26) |
onde, em função à distância ao ponto P, o primeiro termo depende de , o segundo de e os termos seguintes da série de ordem , , etc., são muito menores, uma vez que estamos a considerar o limite de grandes distâncias à região, i.e., . Substituindo esses dois termos na equação (3.20) e colocando fora dos integrais em R os termos que não dependem de , obtém-se:
| (3.27) |
O primeiro integral é a carga total na região R e o segundo integral chama-se momento dipolar da distribuição de carga, pela sua semelhança com o caso de duas cargas pontuais de sinais opostos separadas por uma distância (ver problema 3.3.11 no fim do capítulo):
| (3.28) |
As unidades do momento dipolar são carga vezes distância. Em função da carga total e do momento dipolar, os dois termos dominantes do potencial da distribuição de carga são:
| (3.29) |
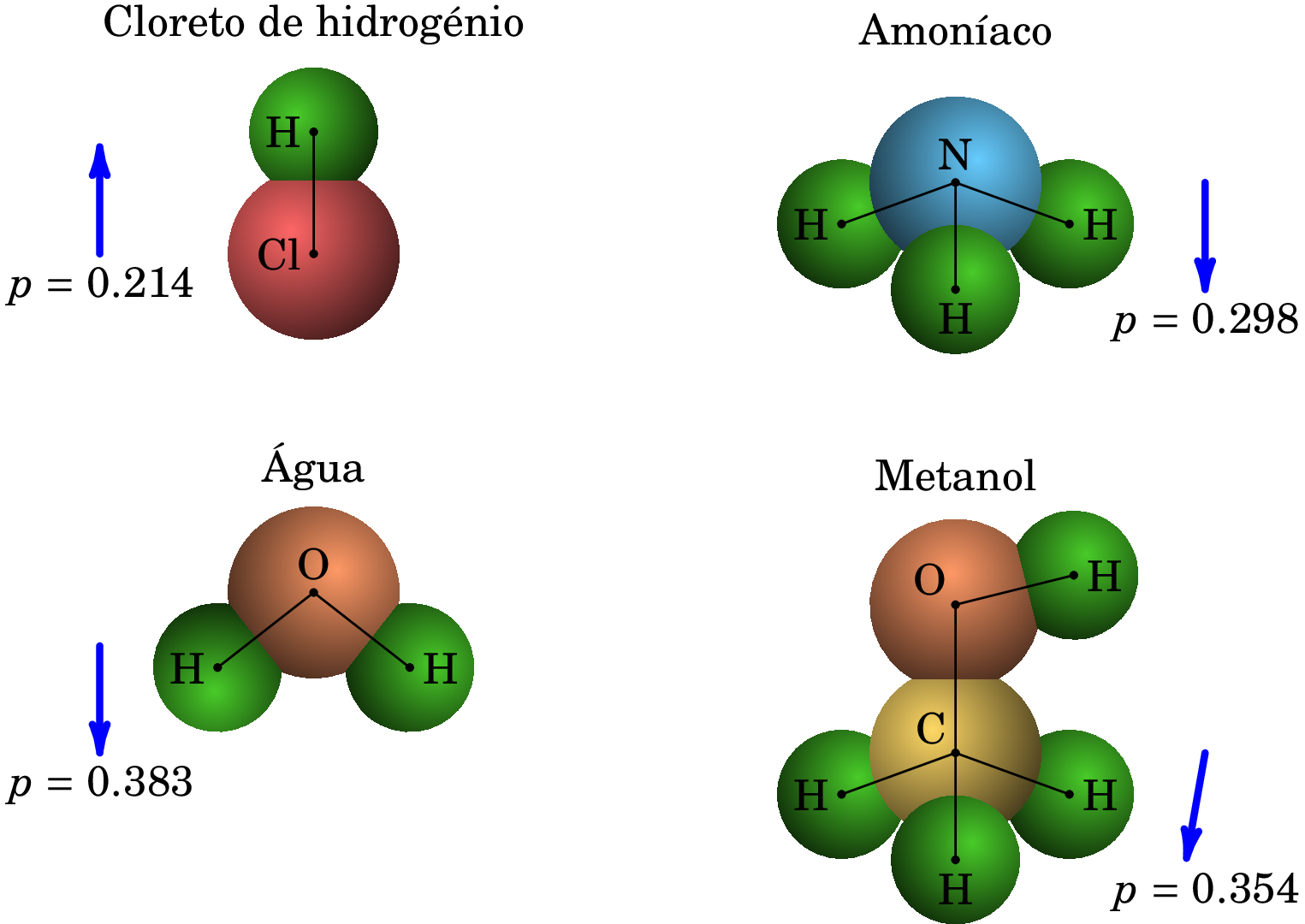
Quando a carga total é diferente de zero, o primeiro termo é muito maior do que o segundo e o sistema é aproximado por uma carga pontual na origem. Nos casos em que a carga total na região é nula, o primeiro termo é nulo e o sistema é aproximado por um dipolo na origem, com momento dipolar definido por (3.28). As moléculas não ionizadas têm todas carga total nula; algumas moléculas, como as que aparecem na figura 3.8 têm momentos dipolares apreciáveis.
Pode-se demonstrar que, quando a carga total é nula, o resultado do integral (3.28) não depende da escolha da origem, embora tenha de ter origem num ponto na região onde há carga.
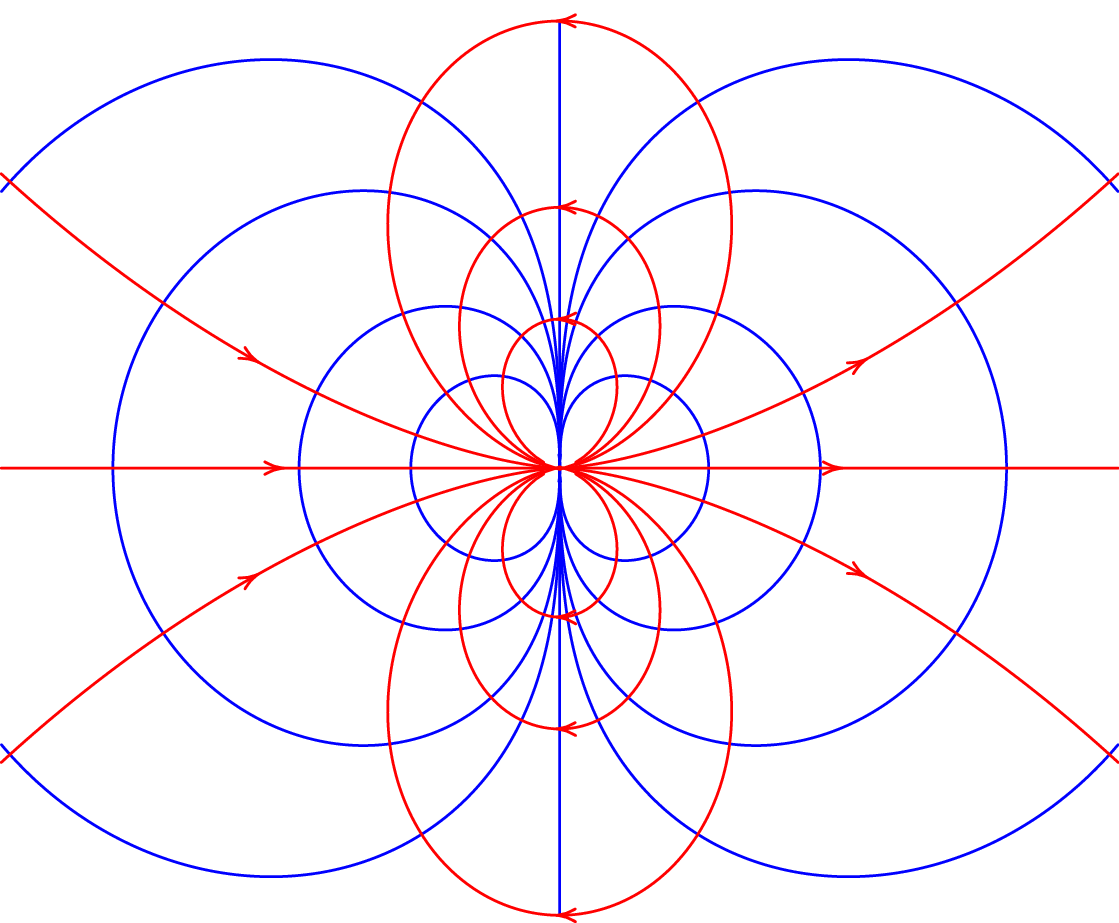
A figura 3.9 mostra as superfícies equipotenciais e linhas de campo elétrico de um dipolo muito pequeno, no plano do momento dipolar , apontando para a direita. As linhas de campo parecem ser fechadas, mas não o são, já que começam na carga positiva, terminam na carga negativa e no interior do dipolo mudam de sentido.
3.7 Equação de Poisson
As Equações (2.30) e (2.39) são as equações básicas da eletrostática. Conhecida a densidade de carga numa dada região do espaço, estas equações são usadas, juntamente com condições apropriadas para o campo elétrico na fronteira dessa região, para determinar o campo elétrico em todos os pontos pertencentes à região do espaço em estudo.
Quando o rotacional de um campo vetorial é sempre nulo (campo conservativo), a identidade (A.87) do apêndice A implica que o campo vetorial é igual ao gradiente de um campo escalar. No caso do campo já vimos que é igual ao gradiente de (equação (3.12)). Substituindo na lei de Gauss (2.30),
| (3.30) |
e usando a identidade (A.90) obtém-se a chamada equação de Poisson:
| (3.31) |
onde é o laplaciano do potencial (A.3.4). Existem, em geral, muitas soluções desta equação diferencial, para uma determinada densidade volúmica de carga dentro de uma região. Para obter uma solução única é necessário impor alguma condição na fronteira, como por exemplo o valor do potencial ao longo da fronteira.
Um caso particular é quando a região de interesse é todo o espaço, e a condição fronteira é no infinito; nesse caso, a solução de (3.31) é a equação (3.20), que foi obtida a partir do potencial de um sistema de cargas pontuais. Na prática não podemos pretender saber a distribuição de carga em todo o espaço, mas apenas numa região finita; para determinar o campo nessa região resolve-se a equação de Poisson, que é uma equação em derivadas parciais. Os métodos de resolução de equações diferenciais parciais encontram-se além dos objetivos deste livro. No capítulo 11, sobre ondas eletromagnéticas, serão estudados alguns exemplos simples de resolução das equações diferenciais parciais do campo eletromagnético.
Exemplo 3.6
O potencial numa região do espaço é (unidades SI). Calcule a carga total dentro de uma esfera com centro na origem e raio .
Resolução. A densidade volúmica de carga determina-se usando a equação de Poisson (equação (3.31)):
| (3.32) |
Para calcular a carga total dentro da esfera, integra-se dentro do seu volume. O integral é mais fácil de calcular em coordenadas esféricas, , em que a coordenada do vetor posição é dada por (expressão (A.58)); assim a expressão da densidade de carga em coordenadas esféricas é
Usando a expressão (A.63) para o elemento infinitesimal de volume em coordenadas esféricas, a carga total dentro da esfera é
3.8 Condutores em equilíbrio eletrostático
Dentro de um condutor isolado o campo elétrico é nulo. Se assim não fosse, existiria movimento das suas cargas livres, cujo efeito seria o de produzir um campo interno dentro do condutor com sentido contrário ao do campo externo.
No exemplo da figura 3.10, um condutor isolado e neutro encontra-se inicialmente numa região onde não há campo elétrico. A seguir, o condutor é sujeito a um campo elétrico externo, o qual faz deslocar as cargas livres do condutor (num condutor metálico, as cargas livres são os eletrões de condução); na figura mostra-se um eletrão de condução a ser deslocado no sentido oposto ao do campo. O movimento das cargas livres conduz à acumulação de cargas de sinais opostos nos dois extremos do condutor, cargas essas que produzem um campo elétrico interno que contraria o campo elétrico externo, fazendo diminuir o campo total dentro do condutor.
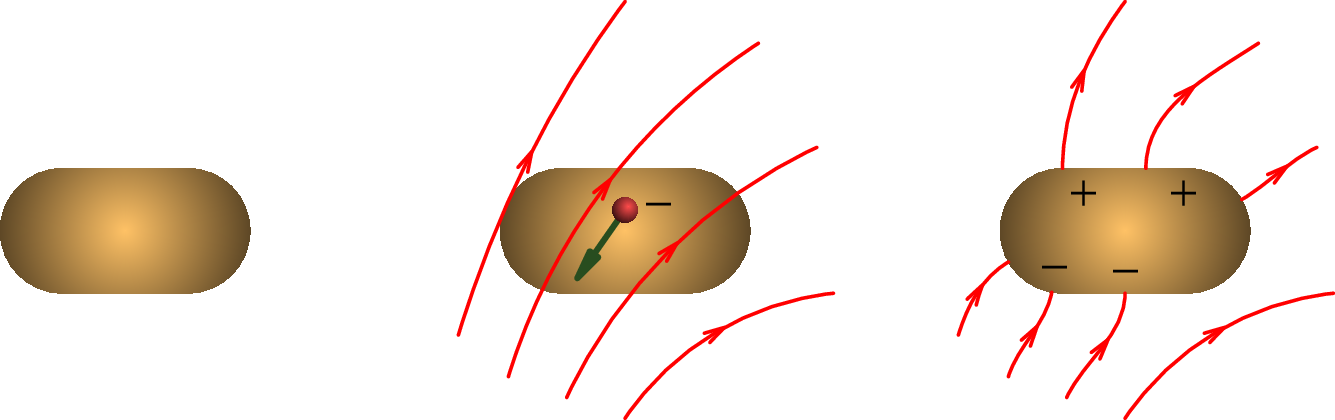
O movimento das cargas livres continuará enquanto o campo total não for nulo, fazendo diminuir ainda mais o campo total, até que chegará um momento em que o campo total seja nulo e o movimento de cargas livres cessa. Quando não há movimento de cargas livres diz-se que o condutor está em equilíbrio eletrostático. Num condutor típico o tempo necessário para atingir o equilíbrio é muito pequeno, da ordem dos segundos.
Resumindo, um condutor encontra-se em equilíbrio eletrostático, quando as suas cargas livres, estão em equilíbrio, i.e., quando a força que atua em cada uma das suas cargas livre é nula. A força atuando em cada carga livre no interior do condutor é dada, usando a expressão geral (1.10), por , onde é o campo elétrico total no interior do condutor. Uma vez em equilíbrio eletrostático, então:
| (3.33) |
Como o campo elétrico é nulo dentro de um condutor em equilíbrio eletrostático, não existem linhas de campo elétrico no interior do condutor e o potencial elétrico em todos os pontos dentro do condutor é o mesmo. Como o potencial elétrico é uma função contínua, o potencial na superfície do condutor, , é igual ao potencial no interior, , do condutor: . O condutor (interior e superfície) é pois um volume equipotencial.
O fluxo em qualquer superfície fechada dentro do condutor é então nulo e, de acordo com a lei de Gauss, não existe carga em nenhum ponto dentro do condutor, donde a densidade volúmica de carga no interior do condutor é sempre nula: . Toda a carga elétrica encontra-se exatamente na superfície do condutor, ou seja, o condutor possui, em geral, uma densidade superficial de carga, , na sua superfície.
A superfície do condutor é uma superfície equipotencial, já que todos os pontos do condutor têm o mesmo potencial, e as linhas de campo elétrico do condutor são portanto perpendiculares à sua superfície. Assim, o campo elétrico na superfície de um condutor em equilíbrio eletrostático possui apenas componente normal à superfície. Note que se o campo elétrico possuisse uma componente tangencial à superfície, as cargas livres na superfície mover-se-iam sobre esta e portanto não haveria equilíbrio eletrostático.
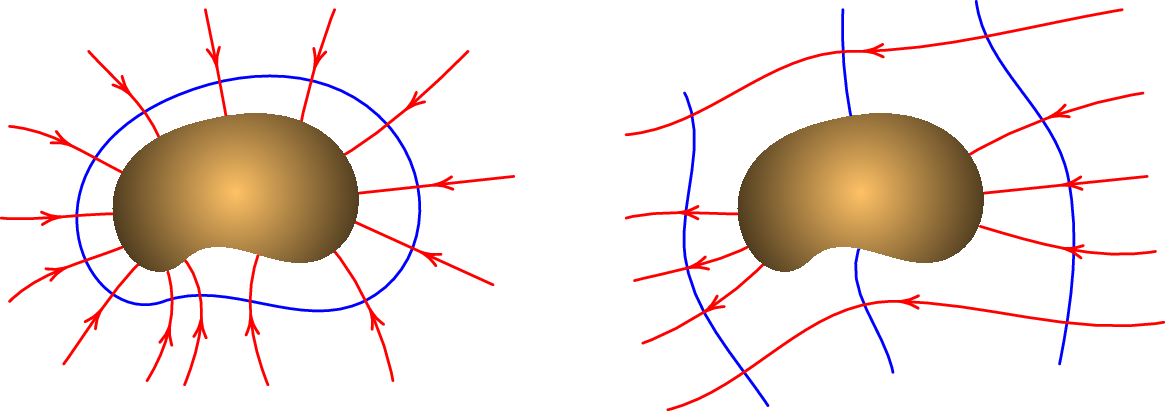
A figura 3.11 mostra as linhas de campo e as superfícies equipotenciais de um condutor com carga negativa e de um condutor neutro sujeito a um campo elétrico externo.
O vetor campo elétrico na superfície de um condutor isolado, , está relacionado com a densidade superficial de carga, , na sua superfície. Para calcular o campo elétrico na superfície, vamos utilizar a Lei de Gauss. Numa pequena região na superfície do condutor as linhas de campo são aproximadamente paralelas e o valor do campo pode ser calculado tal como foi determinado para o campo de um plano infinito no exemplo 2.6 do capítulo 2, calculando o fluxo através de um cilindro com tampas paralelas à superfície, uma dentro e a outra fora do condutor (figura 3.12).
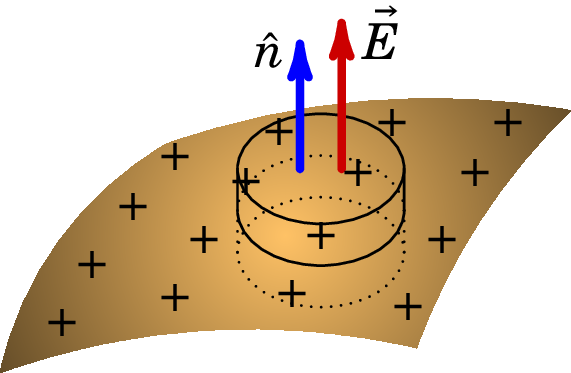
Como neste caso só há fluxo na tampa do cilindro fora do condutor o valor do campo é o dobro do resultado obtido para um plano infinito (ver exemplo (2.6)):
| (3.34) |
onde é o versor normal à superfície do condutor em cada ponto desta (note que como a superfície de um condutor isolado é fechada, então, por definição, aponta sempre para fora da superfície).
Vemos pois que o valor do campo elétrico na superfície de um condutor é diretamente proporcional à densidade superficial de carga. Outra consequência importante da equação (3.34) é que se a carga total de um condutor isolado aumentar, o valor do campo aumentará na mesma proporção e, como tal, o potencial no condutor é diretamente proporcional à carga nele.
A carga não se distribui uniformemente na superfície do condutor, como mostraremos usando um exemplo familiar de um condutor isolado: um automóvel. A carroçaria metálica é condutora e os pneus de borracha são isoladores. A superfície da carroçaria é uma superfície equipotencial e a Terra, que também é condutora, é outra superfície equipotencial.
Se o automóvel estiver carregado, e.g., com carga positiva como na figura 3.13, o potencial naquele tem um valor máximo local. A superfície da carroçaria é uma superfície equipotencial e há outras superfícies equipotenciais à sua volta, com um valor menor. Há linhas de campo a começar em todos os pontos da superfície da carroçaria, sendo perpendiculares a esta.
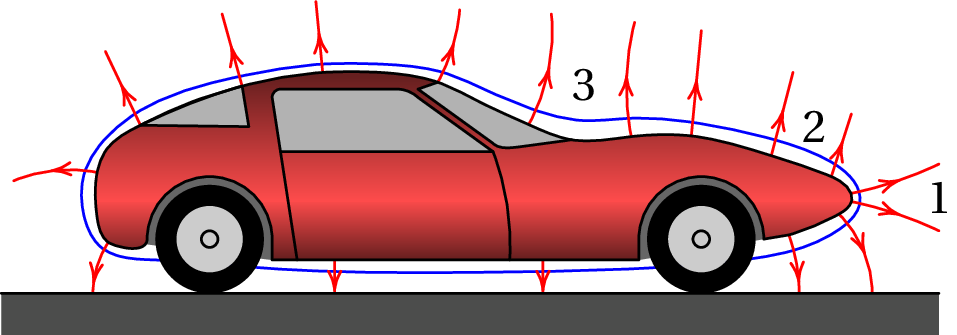
Consideremos as três regiões da superfície do automóvel identificadas na figura 3.13 com os números 1, 2 e 3. Se a densidade superficial de carga fosse igual nessas três regiões, , o módulo do campo (3.34) também seria igual: .
Como pode observar-se na figura 3.13, em 1, onde o condutor é convexo, as linhas de campo afastam-se entre si, ou seja, o campo elétrico diminui em função da distância medida a partir da superfície. Na região 2, onde o condutor é plano, as linhas de campo são paralelas na vizinhança da superfície, o que implica que o campo permanece constante para próximo de zero, mas as linhas acabam por se afastar entre si, fazendo com que comece a diminuir em função de . Na região 3, onde o condutor é côncavo, as linhas de campo inicialmente aproximam-se entre si, antes de começar a se afastar; isso implica que aumenta em função de até um valor máximo, e depois começa a diminuir. O gráfico no lado direito da figura 3.14 mostra como seria , em função de , nessas 3 regiões, no caso em que para .
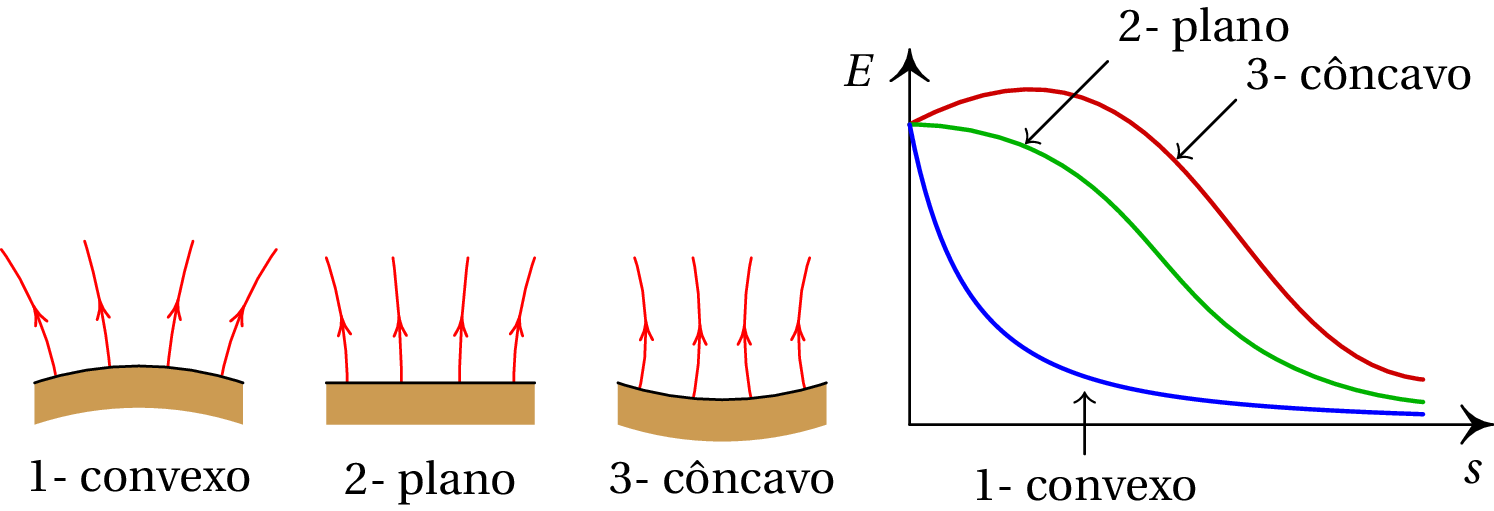
O potencial em cada uma das 3 regiões do condutor é o integral de linha do campo elétrico desde a superfície () até infinito, sendo portanto dado pela área sob cada uma das três curvas no gráfico da figura 3.14. Como tal, o potencial na região 3, onde o condutor é côncavo, seria maior do que na região 2, onde o condutor é plano, e ainda maior do que na região 1, onde o condutor é convexo.
Mas como o potencial nas três regiões tem de ser igual, a área sob cada uma das três curvas tem de ser igual. Conclui-se que o campo na superfície não pode ser igual nas três regiões, e consequentemente a densidade superficial de carga não pode ser a mesma nas três regiões (ver expressão (3.34)). A densidade superficial de carga tem de ser maior na região convexa, menor na região plana, e ainda menor na região côncava. Dessa forma obtém-se o mesmo valor para o integral do campo elétrico nas 3 regiões (figura 3.15).
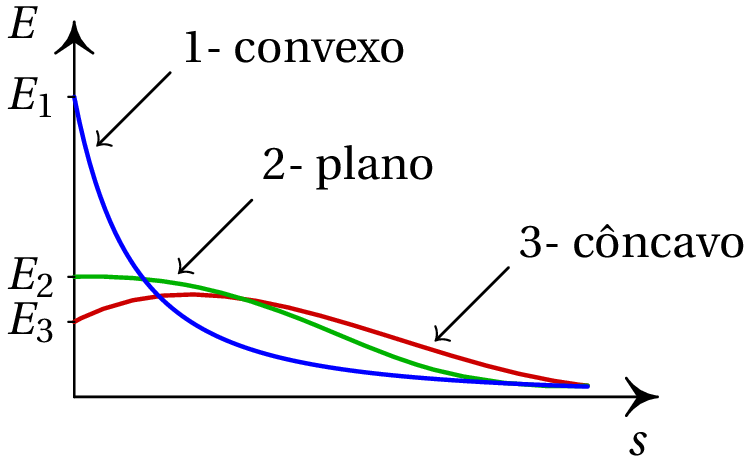
Nas regiões convexas, quanto menor for o raio da curvatura, maior será a densidade superficial de carga, e nas regiões côncavas quanto maior for o raio de curvatura, maior será a densidade superficial de carga. Conclui-se portanto que a carga elétrica se acumula mais nas regiões mais pontiagudas de um condutor, facto este que é designado por efeito de pontas. Esse efeito é o princípio de funcionamento do pára-raios; os raios, constituídos por iões ionizados e eletrões livres, são atraídos para a ponta do pára-raios, onde há uma maior acumulação de cargas e um campo elétrico mais forte.
As forças repulsivas entre as cargas da superfície de um condutor faz com que se exerça uma força na superfície do condutor, para fora deste. Para determinar esta força sobre um elemento infinitesimal de área na superfície do condutor, observe-se que o valor do campo elétrico no condutor dado pelas expressões (3.33) e (3.34) é devido tanto à carga no elemento infinitesimal quanto ao resto da superfície do condutor. A carga infinitesimal do elemento infinitesimal produz por si só um campo elétrico de valor igual a , tanto para dentro como para fora do condutor, à semelhança de um plano infinito (expressão (2.22)).
Conclui-se então que o resto da superfície do condutor, excluindo o elemento infinitesimal , tem de produzir na superfície do condutor um campo elétrico de valor na direção de dentro para fora do condutor, o qual no interior do condutor se anula com o campo do elemento infinitesimal e no exterior se soma a este, produzindo assim o campo total na superfície do condutor dado pelas expressões (3.33) e (3.34).
A força elétrica infinitesimal que atua no elemento infinitesimal de área calcula-se usando devidamente a expressão geral (1.10), i.e., multiplicando a carga no elemento infintesimal pelo o valor do campo produzido pelo resto da superfície do condutor, sem incluir o campo do próprio elemento infinitesimal:
| (3.35) |
Esta força é sempre para fora do condutor, i.e., , independentemente do sinal da densidade superficial de carga. A expressão (3.35) pode ser interpretada como uma pressão exercida em cada ponto da superfíce do condutor (com sentido para fora do condutor) dada por:
| (3.36) |
Esta pressão denomina-se por pressão eletrostática. Como a densidade superficial de carga depende de ponto para ponto na superfície, o mesmo ocorre com a força e a pressão eletrostáticas que se exercem sobre a superfície do condutor. Note-se ainda que quer a força quer a pressão eletrostática são porporcionais ao quadrado da densidade superficial de carga na superfície do condutor.
Problemas
-
3.1.
Demonstre a identidade (3.14):
-
3.2.
Uma esfera metálica encontra-se próxima de outra peça metálica formada por um cilindro e duas semiesferas, como mostra a figura. Ambos objetos estão isolados de qualquer outro condutor. A esfera tem carga positiva () e a peça cilíndrica está completamente descarregada (). Arbitrando que o potencial da peça cilíndrica é zero, então o potencial da esfera é 80 V. Faça um desenho mostrando as duas peças, a distribuição de cargas, as linhas de campo nas duas peças e à sua volta, e as superfícies equipotenciais de -5 V, 5 V e 75 V.
-
3.3.
O potencial elétrico a uma certa distância de uma carga pontual é 600 V (arbitrando potencial nulo no infinito) e o valor do campo elétrico é 200 N/C. Calcule a distância e o valor da carga.
-
3.4.
A figura representa as linhas de campo eletrostático de duas partículas carregadas e separadas por uma distância de 7 cm.
(a) Calcule a distância do ponto P às partículas.
(b) Sabendo que a carga da partícula no lado direito é de nC, calcule o potencial no ponto P (arbitre no infinito).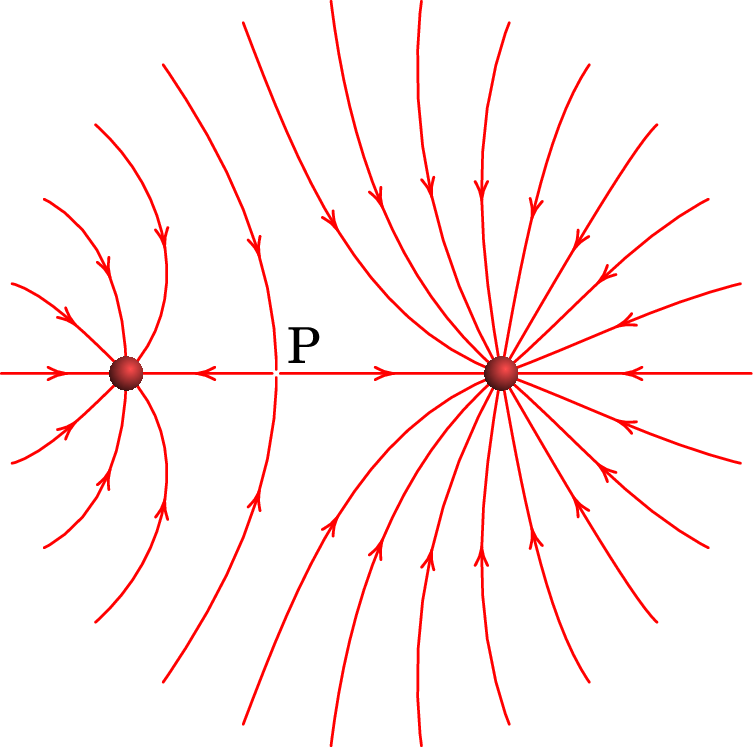
-
3.5.
Duas superfícies condutoras esféricas e concêntricas têm raios de 5 cm e 7 cm. A superfície menor tem carga total de 3 nC e a carga total na superfície maior é nC. Qual é a diferença de potencial entre as duas superfícies?
-
3.6.
A figura na capa deste livro é a representação gráfica das linhas de campo e superfícies equipotenciais do seguinte potencial sobre o plano :
Explique a que tipo de sistema corresponde este potencial e encontre a expressão do campo elétrico em qualquer ponto do plano .
-
3.7.
A figura mostra as superfícies equipotenciais de uma carga pontual no interior de um campo elétrico uniforme . A grandes distâncias da carga pontual as superfícies são planos paralelos distanciados 8 cm.
(a) Calcule o módulo e a direção do campo externo .
(b) Diga se a carga pontual é positiva ou negativa. Justifique.
(c) Qual é a direção da força sobre a carga pontual?
(d) Sabendo que a distância entre a carga pontual e o ponto P é 9 cm, calcule o valor da carga pontual.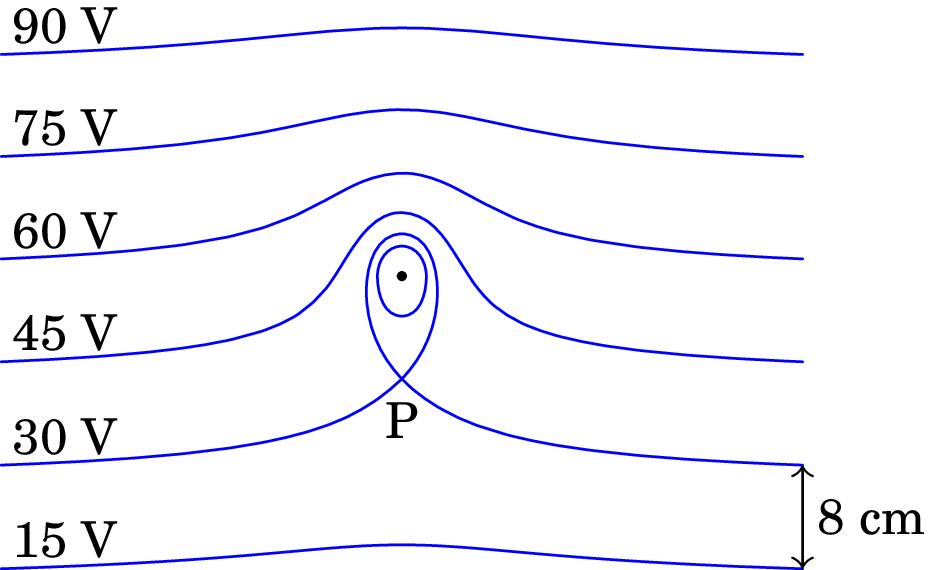
-
3.8.
Mostre que o campo elétrico , em que é uma constante e o vetor posição, é conservativo. Calcule o potencial correspondente a este campo.
-
3.9.
Um disco de raio tem carga superficial uniforme. Determine o potencial e o campo elétrico num ponto qualquer P ao longo do eixo longitudinal do disco.
-
3.10.
As três figuras seguintes representam as superfícies equipotenciais de três sistemas de duas cargas pontuais (esquerda) e (direita). Em todos os casos nC, e a distância entre as duas cargas é 6 cm. Nas figuras () e () a distância entre o ponto P e a carga é igual a 2 cm. Determine o valor de nos três casos.
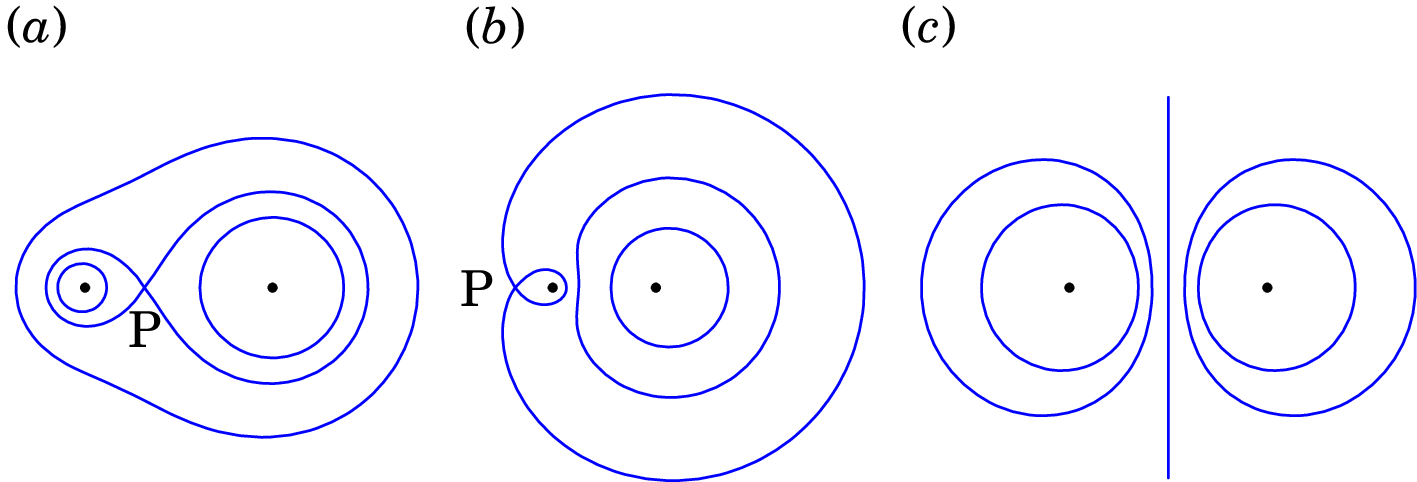
-
3.11.
Um dipolo elétrico é formado por duas cargas pontuais e a uma distância . Para determinar o potencial a uma distância do centro do dipolo, admita que as cargas estão no eixo , em e tal como mostra a figura, onde é o vetor desde a carga negativa até à carga positiva.
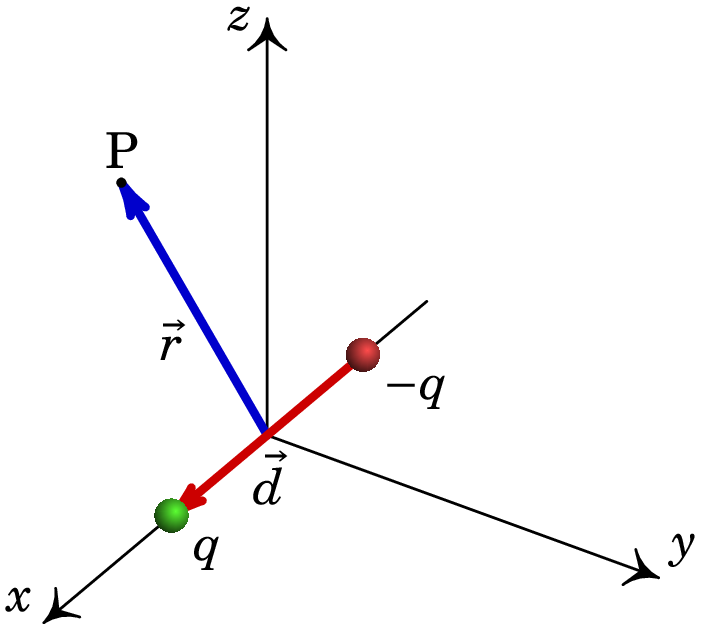
(a) Determine a expressão do potencial elétrico no ponto P de vetor posição , em função de , e .
(b) Mostre que no limite o potencial é:onde é o momento dipolar. (Sugestão: escreva as raízes nos denominadores da forma com e use a série do binómio de Newton.)
(c) Calcule o campo elétrico correspondente ao potencial na alínea anterior. (Sugestão: expresse as componentes cartesianas dos vetores e , calcule o gradiente em coordenadas cartesianas e a seguir escreva o resultado em função dos vetores e ).Note-se que os resultados das alíneas (b) e (c) não dependem da distância e são válidos até quando se aproximar de zero, como no caso de um dipolo molecular.
-
3.12.
A expressão do campo elétrico numa região é
(a) Mostre que o campo é conservativo.
(b) Determine a expressão do potencial eletrostático. -
3.13.
Usando a expressão do gradiente em coordenadas esféricas (apêndice A), encontre o campo elétrico correspondente ao potencial (onde e são constantes):
-
3.14.
Usando a expressão do gradiente em coordenadas cilíndricas (apêndice A), encontre o campo elétrico correspondente ao potencial:
-
3.15.
Determine as condições que devem cumprir as componentes esféricas de um campo vetorial para ser campo conservativo.
-
3.16.
O potencial dentro do cubo , , é
onde e são constantes. Calcule a carga total dentro do cubo.
-
3.17.
Diga quais dos seguintes campos podem ser campos eletrostáticos. Nos casos afirmativos, calcule a densidade volúmica de carga que produz esse campo ( e são constantes):
(a) .
(b) .
(c) . -
3.18.
No espaço tridimensional , existe um potencial eletrostático dado por:
onde e são constantes positivas. Determine:
(a) O campo elétrico associado a este potencial.
(b) A densidade volúmica de carga em qualquer ponto.
Descreva a região onde existe carga elétrica.
(c) Represente os gráficos das funções obtidas nas alíneas (a) e (b).
Respostas
-
3.1.
Em coordenadas cartesianas, e calculando as 3 derivadas parciais obtém-se o resultado.
-
3.2.
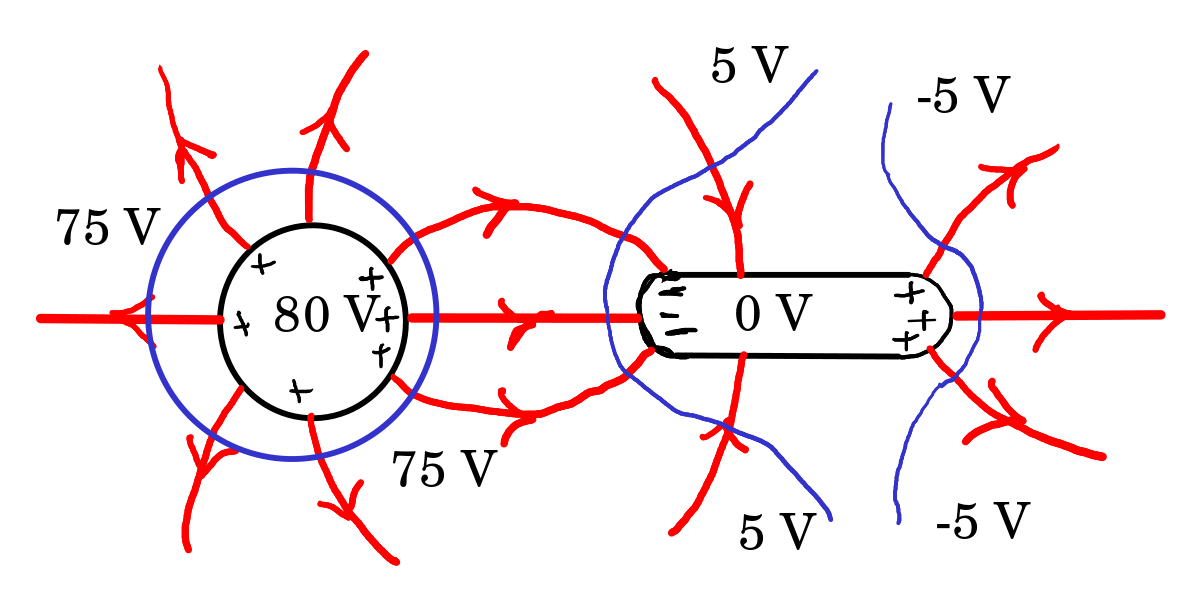
-
3.3.
3 m, 200 nC.
-
3.4.
(a) cm e cm. (b) V.
-
3.5.
154 V.
-
3.6.
Trata-se de um dipolo na origem, com momento dipolar na direção do eixo , e uma carga pontual na origem.
(em V/m) -
3.7.
(a) V/m, para baixo. (b) negativa. (c) para cima. (d) nC.
-
3.8.
Arbitrando o potencial nulo na origem do sistema de coordenadas usado, i.e, , então .
-
3.9.
, , onde aponta para fora da superfície do disco em ambos os lados.
-
3.10.
(a) 12 nC. (b) nC. () nC.
-
3.11.
(a)
(b) Observe que no primeiro termo,
e de forma semelhante para o segundo termo.
(c) -
3.12.
(b) , arbitrando no infinito.
-
3.13.
.
-
3.14.
.
-
3.15.
, , .
-
3.16.
.
-
3.17.
(a) Sim. .
(b) Não é campo eletrostático.
(c) Sim. . -
3.18.
(a) , onde
(b)
A região do espaço tridimensional onde existe carga elétrica, corresponde a um paralelepípedo de largura entre e de dimensões infinitas em e em . Corresponde pois a um "plano infinito" paralelo ao plano O, mas com uma espessura finita de .
(c)