5. Força eletromotriz, corrente e resistência

Alessandro Volta (1745–1827)
O biólogo Luigi Galvani (1737–1798), enquanto cortava a perna de uma rã morta, observou que esta se encolhia bruscamente como se estivesse viva. Galvani atribuiu o efeito a uma eletricidade de origem animal. Volta demonstrou que a origem desse fenómeno era o movimento de cargas elétricas na perna da rã, quando posta em contacto com dois metais diferentes — o da faca e o da mesa, a qual era metálica. Aproveitando este efeito, Volta constrói a primeira pilha química em 1800, dando origem ao rápido desenvolvimento da tecnologia elétrica nas primeiras décadas do século XIX.
5.1 Pilhas químicas
Um dos avanços mais importantes no estudo da eletricidade foi a invenção de Volta das pilhas químicas, no fim do século XVIII. As pilhas químicas permitiam manter fluxo constante de cargas num condutor, contrariando as forças dissipativas nele, algo que até então era impossível.
A primeira pilha de Volta foi feita colocando discos de zinco e de cobre, sobrepostos e separados entre si por discos de cartão molhado numa solução ácida (figura 5.1). Repetindo a mesma sequência de discos várias vezes, consegue-se produzir passagem de carga (corrente elétrica) suficientemente elevada para que os seus efeitos sejam visíveis. Por exemplo, Volta colocava as suas mãos dentro de dois recipientes com água salgada, ligados aos dois terminais da sua pilha e o choque elétrico nas suas mãos tornava-se doloroso quando a pilha era formada por mais de 20 grupos de discos de cobre e zinco.
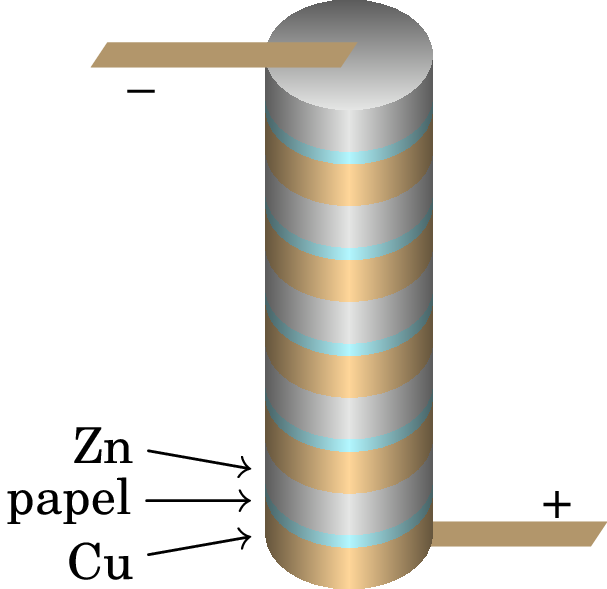
O princípio de funcionamento duma pilha química é a utilização de dois metais diferentes (condutores portanto), chamados elétrodos, separados e em contacto com uma substância com iões positivos e negativos, sendo esta portanto condutora, chamada eletrólito. O eletrólito oxida um dos elétrodos e reduz o outro. No caso da pilha de Volta, há oxidação no elétrodo de zinco e redução no elétrodo de cobre.
Os iões positivos do eletrólito (catiões) reagem com o elétrodo de cobre, que passa a ser o cátodo da pilha, i.e., o terminal positivo da pilha, e os iões negativos (aniões) reagem com o elétrodo de zinco, que passa a ser o ânodo da pilha, i.e., o terminal negativo da pilha.
A reação do elétrodo de cobre com os catiões do eletrólito é uma reação de redução, ocorrendo transferência de eletrões de condução do elétrodo para o eletrólito, acumulando o elétrodo de cobre carga positiva, funcionando portanto como cátodo. No elétrodo de zinco, a reação deste com os aniões do eletrólito é uma reação de oxidação, na qual são transferidos eletrões de condução do eletrólito para o elétrodo, o qual acumula carga negativa, funcionando assim como ânodo. No estado de equilíbrio, as cargas nos elétrodos impedem a ocorrência de mais reações.
Quando se acabam os reagentes das reações químicas de oxidação e redução numa pilha, em particular as concentrações de iões no eletrólito, a pilha encontra-se completamente descarregada. Se as reações químicas envolvidas forem reversíveis, então a pilha pode ser recarregada, invertendo-se para tal o sentido das reações químicas através do fornecimento de energia elétrica à pilha e restaurando-se assim a sua composição original. Contudo, as pilhas recarregáveis não podem ser recarregadas indefinidamente. Isto acontece devido, em grande parte, à diminuição dos reagentes, à perda de eletrólito e à corrosão interna na pilha. Cada ciclo de carga-descarga vai viciando a pilha.
5.2 Força eletromotriz
A energia associada a uma reação de redução de um elétrodo com um eletrólito depende do tipo de elétrodos e de eletrólito. Esta energia dividida pelo valor da carga elétrica envolvida na reação tem unidades de potencial elétrico e chama-se potencial de redução, . Por seu lado, a reação de oxidação possui associado o potencial de oxidação, , o qual é igual ao simétrico do potencial de redução, .
Numa pilha com dois elétrodos de condutores diferentes, o cátodo será o que tiver maior potencial de redução e o ânodo o que o tiver menor: . O potencial associado à reação conjunta no dois elétrodos, redução no cátodo e oxidação no ânodo, é então dado por:
| (5.1) |
Esta diferença de potencial entre os elétrodos depende do material dos elétrodos e do eletrólito e chama-se força eletromotriz da pilha, ou de forma abreviada f.e.m., sendo denotada pela letra grega . Note-se que a força eletromotriz é uma diferença de potencial, cuja sua unidade SI é o volt e não o newton, como erradamente o seu nome poderia sugerir. O valor da f.e.m. para a maioria das pilhas encontra-se entre 1 volt e 4 volt.
Consegue-se construir pilhas com f.e.m. de vários volt ligando várias pilhas em série, tal como a pilha de Volta na figura 5.1. A f.e.m. de um único conjunto de discos de cobre e zinco com um disco de papel húmido no meio é de aproximadamente 1.1 V. O lado esquerdo da figura 5.2 mostra o diagrama de circuito usado para representar essa pilha; a barra maior e mais comprida é o terminal positivo e a barra mais grossa e menos comprida é o terminal negativo. O lado direito da figura mostra-se um diagrama habitual para representar as 5 dessas pilhas ligadas em série da figura 5.1, que é equivalente a ter uma única pilha com f.e.m. de 5.5 V.
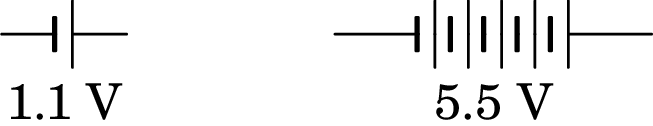
A f.e.m. de uma pilha não depende do tamanho nem da separação dos elétrodos, mas diminui à medida que a concentração de iões no eletrólito diminui. A tabela 5.1 mostra os materiais dos elétrodos e do eletrólito em vários tipos de pilhas usadas atualmente e os valores da f.e.m. obtida em cada caso.
| Tipo | cátodo | ânodo | eletrólito | f.e.m. |
| (V) | ||||
| seca | C | Zn | MnO / NHCl | 1.5 |
| alcalina | C | MnO | KOH | 1.5 |
| mercúrio | HgO | Zn | NaOH | 1.35 |
| óxido de prata | AgO | Zn | NaOH | 1.35 |
| NiCd | NiO | Cd | KOH | 1.2 |
| NiMH | NiO | liga metálica | KOH | 1.2 |
| iões de lítio | LiO / Co | C | Li | 3.7 |
(Fonte: Linden e Reddy 2001.)
A carga armazenada numa pilha corresponde à carga total dos iões positivos, (igual ao valor absoluto da carga dos iões negativos) no eletrólito. Por outras palavras, a carga armazenada é igual à carga acumulada no cátodo, sendo a carga acumulada no ânodo . O cátodo encontra-se a um potencial elétrico e o ânodo encontra-se ao potencial . A energia potencial elétrica armazenada numa pilha é a energia potencial associada à carga armazenada, a qual, segundo a expressão (4.4), é dada por:
| (5.2) |
onde foi usado a definiçao de f.e.m., expressão (5.1).
Outra caraterística importante de cada pilha, para além da sua f.e.m. , é a carga máxima que esta consegue armazenar, , a qual indica a carga total dos iões positivos (igual ao valor absoluto da carga dos iões negativos) no eletrólito, quando o eletrólito contiver o máximo número possível de iões. A energia elétrica associada à carga máxima é a energia máxima que a pilha pode armazenar, sendo portanto dada por:
| (5.3) |
onde se usou a expresão (5.2).
5.3 Corrente elétrica
Quando uma pilha é ligada a um dispositivo elétrico, tal como se mostra na figura 5.3, o excesso de eletrões de condução no terminal negativo da pilha passará através do dispositivo para o terminal positivo da pilha, fazendo diminuir quer a carga negativa do terminal negativo quer a carga positiva do terminal positivo. Enquanto ainda houver iões no eletrólito, ocorrerão reações químicas nos elétrodos que repõem a carga positiva e negativa dos terminais da pilha.
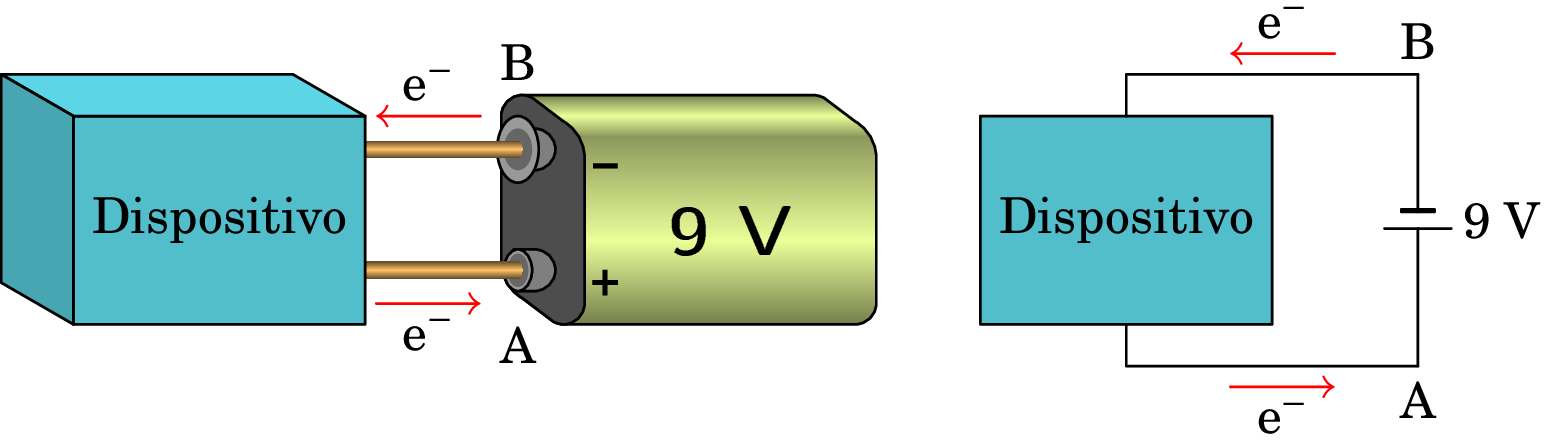
Os eletrões perdem energia potencial elétrica na passagem do terminal negativo para o positivo através do dispositivo. A energia potencial perdida por cada eletrão que circula através do dispositivo, usando a expressão (4.4), é dada por
| (5.4) |
onde é a carga elementar.
Como veremos mais adiante, a velocidade média dos eletrões de condução é constante, pelo que a sua variação de energia cinética é nula. Se o dispositivo for passivo (i.e., se este não contiver fontes de f.e.m.) existem neste forças dissipativas que contrariam o movimento dos eletrões de condução. O trabalho realizado por estas forças dissipativas (i.e., não conservativas) é então igual à energia potencial perdida por cada eletrão quando circula pelo dispositivo: . Por outro lado, a energia potencial ganha por cada eletrão que “atravessa” a pilha, usando a expressão (4.4), é dada por
| (5.5) |
Assim, a energia que a pilha fornece a cada eletrão que a “atravessa” é dada por:
| (5.6) |
Deste modo, vemos que a pilha fornece aos eletrões a mesma energia que estes perdem quando circulam através do dispositivo, mantendo-se assim o movimento constante de eletrões. Note-se que a pilha perde energia por cada eletrão que a “atravessa” igual a , pelo que se encontra a descarregar.
A passagem de cargas através do dispositivo constitui a corrente elétrica, com intensidade definida como o valor absoluto da carga total transferida por unidade de tempo:
| (5.7) |
Na figura 5.3, a passagem de eletrões durante um intervalo de tempo implica carga que que passa do elétrodo negativo para positivo. A diminuição da carga do elétrodo negativo é e a carga no elétrodo negativo também diminui nessa mesma quantidade. A situação é exatamente equivalente à situação em que tivesse passado carga positiva do elétrodo positivo para o elétrodo negativo. Como tal, independentemente do sinal da carga que é transportada define-se o sentido da corrente elétrica no sentido do campo elétrico, que é o sentido do deslocamento das cargas positivas, oposto ao sentido do deslocamento das cargas negativas.
A carga total que circula no dispositivo num intervalo de tempo entre e é o integral da corrente elétrica nesse intervalo:
| (5.8) |
observe-se que se durante o intervalo de tempo a corrente muda de sentido, o sinal da corrente também muda.
E a energia elétrica fornecida pela fonte de f.e.m. durante esse intervalo, usando a expressão (5.2), é dada por:
| (5.9) |
A unidade de corrente elétrica no Sistema Internacional de unidades é o ampere, representado pela letra A
| (5.10) |
Por exemplo, num condutor com corrente de durante 5 segundos passa uma carga total de coulomb através do condutor. Como um coulomb é igual a um ampere vezes um segundo, outra unidade de carga muito útil no caso dos circuitos elétricos é o ampere vezes hora (A·h), igual a 3600 C.
Exemplo 5.1
Numa lâmpada fluorescente de 3 cm de diâmetro, sabendo que existe um fluxo de eletrões por segundo, e um fluxo de iões (de carga ) por segundo. Calcule a corrente elétrica na lâmpada.
Resolução. O gás ionizado dentro da lâmpada é um condutor com portadores de carga positiva e negativa, como mostra a figura seguinte
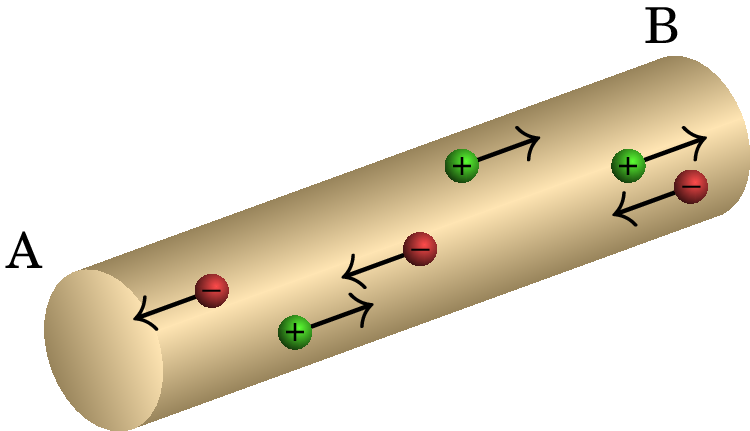
O movimento dos iões e eletrões através da lâmpada é produzido pela diferença de potencial entre os seus terminais A e B. Os eletrões deslocam-se para o terminal com maior potencial, enquanto os iões positivos deslocam-se no sentido oposto, pelo que .
As duas correntes, eletrónica e iónica, têm assim o mesmo sentido. A corrente total é a soma da corrente devida à passagem de eletrões (), mais a corrente e a corrente devida à passagem de iões positivos ():
Calcula-se a intensidade de cada uma dessas correntes multiplicando o número de partículas que passam a cada segundo, vezes o valor absoluto da carga de cada partícula:
Nos fios condutores que ligam as extremidades A e B da lâmpada à fonte elétrica existe um fluxo de eletrões correspondente à corrente total 0.400 A, ou seja, um fluxo de .
Assim, em cada segundo entram na lâmpada eletrões pelo ponto B (vindos do fio condutor ligado a este ponto), dos quais percorrem a lâmpada de B até A e os restantes recombinam-se com os iões que se deslocam em sentido contrário desde o ponto A até ao ponto B, dando origem a de átomos neutros.
Em cada segundo, o mesmo número de átomos neutros () são ionizados no ponto A, dando origem a eletrões e ao mesmo número de iões. Os eletrões libertados na ionização de átomos neutros mais os eletrões que percorrem a lâmpada desde B até A, saem pelo ponto A, indo para o fio condutor ligado a este ponto, enquanto que os iões resultantes da ionização se deslocam de A para B.
Se o sistema estiver em equilíbrio, existirá também um fluxo de átomos neutros por segundo, desde o ponto B até ao ponto A.
O fluxo total de massa é de eletrões por segundo desde o ponto B até ao ponto A ( eletrões de condução mais transportados pelos átomos neutros), o qual é igual ao fluxo total de massa nos fios condutores ( eletrões por segundo), como deve ser devido à conservação de massa.
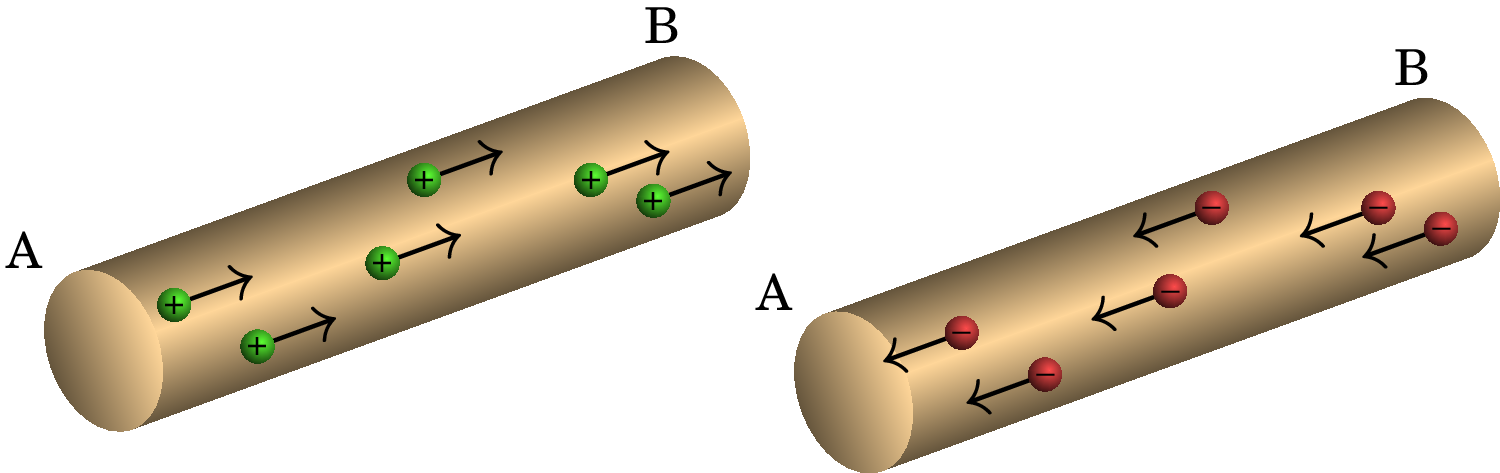
A lâmpada do exemplo anterior é um condutor com cargas de condução positivas e negativas. Existem também condutores em que todas as cargas de condução são negativas, tal como os metais, e ainda condutores em que todas as cargas de condução são positivas, tal como os semicondutores tipo p. A figura 5.4 mostra dois condutores com cargas de condução positivas e negativas. Se o potencial no extremo A desses condutores for maior do que o potencial do extremo B, tal como na lâmpada do exemplo, e o fluxo de cargas de condução por cada segundo fosse , a corrente nos três casos terá a mesma intensidade, 0.400 A, e possuirá a direção e o sentido de A para B, i.e., do maior potencial para o menor. Por simplicidade, sempre que houver corrente num condutor podemos admitir que as cargas de condução são positivas e deslocam-se no sentido da corrente.
Se o dispositivo na figura 5.3 for ativo (i.e., se este contiver fontes de f.e.m.), poderá estar ligado de forma a contrariar o movimento das cargas fornecidas pela pilha. Neste caso, os eletrões de condução saem do terminal positivo da pilha, circulam pelo dispositivo e chegam ao terminal negativo da pilha com maior energia potencial elétrica, a qual é fornecida pelo dispositivo ativo.
Neste caso, cada eletrão quando “atravessa” a pilha perde energia, a qual, usando a expressão (4.4), é dada por
| (5.11) |
A energia perdida pelo eletrão ao “atravessar” a pilha é absorvida por esta:
| (5.12) |
Neste caso, a pilha encontra-se portanto a carregar.
Se as reações nos elétrodos da pilha forem reversíveis, diz-se que a pilha é recarregável; a reação em cada elétrodo será a reação inversa de quando a pilha estava a descarregar e a concentração de iões no eletrólito aumentará, em vez de diminuir. A pilha será assim recarregada.
Os tipos de pilhas nas três últimas linhas da tabela 5.1 são recarregáveis. Numa pilha não recarregável, a inversão do sentido da corrente apenas aquece a pilha, mas não a recarrega.
Outro exemplo de pilha química recarregável é a bateria de um automóvel, com elétrodo negativo de chumbo (Pb), elétrodo positivo de dióxido de chumbo ) e eletrólito líquido de ácido sulfúrico () em em solução aquosa. Quando a bateria está a fornecer corrente, as reações de redução no terminal positivo e oxidação no terminal negativo são as seguintes:
| (5.13) | ||||
| (5.14) |
os dois eletrões envolvidos nessas reações circulam pelo circuito externo ligado à bateria, do elétrodo negativo para o positivo (corrente do elétrodo positivo para o negativo).
Por cada dois eletrões que circulam no circuito, duas moléculas de ácido sulfúrico do eletrólito da bateria reagem com o metal dos elétrodos, produzindo duas moléculas de água e duas moléculas de sulfato de chumbo, insolúveis, que ficam aderidas aos elétrodos. A bateria descarrega à medida que a concentração de ácido no eletrólito diminui.
Quando a bateria está a ser recarregada, a corrente no circuito externo circula do terminal negativo para o positivo, há passagem de eletrões do elétrodo positivo para o negativo e as reações nos elétrodos são as reações inversas do caso anterior:
| (5.15) | ||||
| (5.16) |
Ao recarregar a bateria, o sulfato de chumbo acumulado nos elétrodos desaparece, e a concentração de ácido no eletrólito aumenta. De referir que quando a bateria está a ser recarregada, o elétrodo positivo, que é o catodo quando a bateria está a descarregar, passa a ser considerado ânodo, e o elétrodo negativo cátodo. A razão é porque quando a bateria esta a ser recarregada, os catiões do eletrólito deslocam-se para o elétrodo negativo e os aniões para o elétrodo positivo. Por isso, é melhor falar de elétrodos positivo e negativo, em vez de cátodo e ânodo.
5.4 Densidade de corrente
Num fio condutor como o da figura 5.5, se houver diferença de potencial entre os extremos do fio, haverá corrente elétrica do ponto a maior potencial para o ponto a menor potencial. No caso da figura, temos então que .
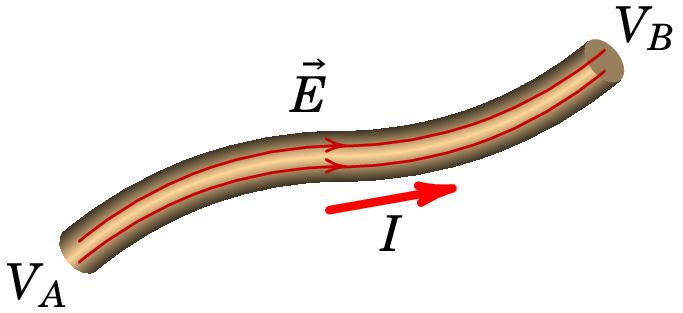
As cargas de condução do condutor são uma nuvem muito densa, incompressível, tal como a água num tubo. Como tal, a cada intervalo de tempo , a carga que entra por um extremo é exatamente igual há carga que sai pelo outro extremo, pois não há acumulação ou produção de carga elétrica em nenhuma parte do condutor; este tipo de corrente é designada por corrente elétrica estacionária, embora possa ser diferente em diferentes instantes de tempo (corrente elétrica variável no tempo).
As linhas de campo elétrico passam pelo interior do fio, desde o extremo a maior potencial até ao extremo a menor potencial e não podem atravessar as paredes laterais do fio para fora deste, nem começar nas paredes laterais para dentro do fio, porque isto implicaria acumulação ou produção de carga nessas paredes, respetivamente.
Se nalguma parte o fio for mais estreito, as linhas de campo ficarão mais próximas e a intensidade do campo será maior; a velocidade da nuvem de cargas de condução também terá de ser maior, para que no intervalo de passe a mesma carga que está a passar em qualquer outra parte do fio, já que a área da secção transversal, , será menor nessa parte do fio.
Num ponto qualquer do fio, com secção transversal de área , a carga que passa durante o intervalo é igual à carga no volume de um cilindro com base igual à secção transversal do fio e altura , igual ao deslocamento da nuvem de cargas de condução durante o intervalo (ver figura 5.6).
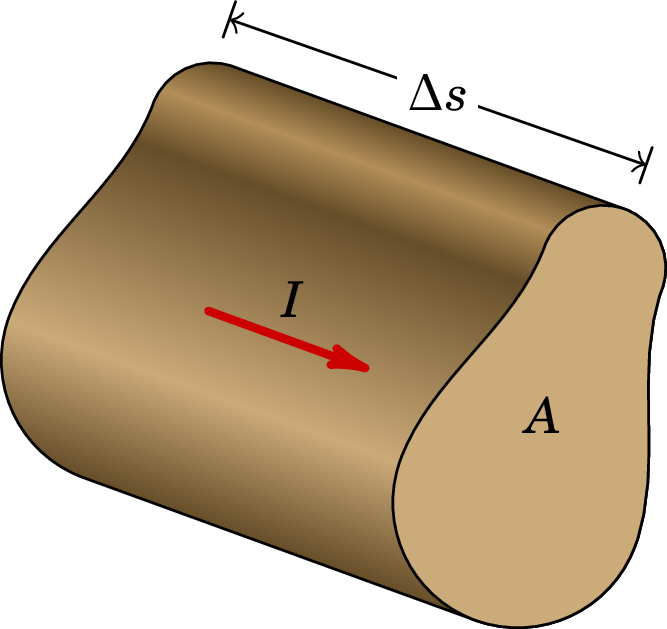
Se a densidade volúmica de carga da nuvem de condução for , então a carga que passa pela área é dada por:
| (5.17) |
O deslocamento da nuvem de carga de condução durante o intervalo é igual a , onde é o módulo da velocidade da nuvem de condução, considerada constante se for suficientemente pequeno. Substituindo em (5.17) e dividindo por , obtém-se,
| (5.18) |
O produto da densidade volúmica das cargas de condução vezes a sua velocidade é designado por densidade de corrente elétrica :
| (5.19) |
e é igual à intensidade da corrente dividida pela área da secção transversal do fio. As unidades SI de J são pois A/m.
O conceito de densidade de corrente pode ser generalizado a qualquer situação em que exista uma distribuição de carga, que pode ter diferentes velocidades em diferentes pontos, com diferentes direções. Nesse caso a densidade de corrente elétrica é um campo vetorial que em cada ponto é igual à densidade volúmica de carga nesse ponto vezes a velocidade da carga nesse ponto:
| (5.20) |
Dadas as propriedades (5.19) e (5.20) do vetor densidade de corrente , o fluxo do campo através de uma superfície S é igual à corrente elétrica que atravessa essa mesma superfície:
| (5.21) |
Ou seja, o fluxo do campo é igual à carga elétrica que atravessa a superfície S por unidade de tempo. De facto, a expressão (5.21) é a definição mais geral de corrente elétrica, sendo a expressão (5.7) um caso particular.
Numa superfície fechada S, o integral de superfície de , i.e., o seu fluxo, será igual à carga total que sai da superfície menos a carga total que entra por unidade de tempo. Devido à conservação da carga, a carga que sai através da superfície fechada S menos a carga que entra nesta deverá ser igual a menos a variação da carga no interior, , da região delimitada por S por unidade de tempo:
| (5.22) |
A equação (5.22) chama-se equação de continuidade, e traduz o princípio da conservação da carga elétrica. A equação de continuidade pode ser escrita na forma diferencial (ou forma local). Notando que
| (5.23) |
onde R é a região delimitada pela superfície fechada S e usando o teorema da divergência (A.75), temos então que:
| (5.24) |
Exemplo 5.2
A intensidade da corrente num fio de cobre de raio é . Determine a densidade de corrente e a velocidade média dos eletrões de condução, sabendo que a massa atómica do cobre é , a sua densidade volúmica de massa e por cada átomo de cobre existe aproximadamente um eletrão de condução.
Resolução: A densidade de corrente é,
Por cada átomo de cobre existe um eletrão de condução, logo, por cada mole de cobre existem (número de Avogadro) eletrões de condução.
Lembrando que a massa atómica de um dado elemento corresponde à massa em gramas de uma mole de átomos desse elemento, o número de eletrões de condução por grama de cobre é então dado por:
A densidade volúmica de eletrões de condução (número de eletrões de condução por unidade de volume) é o produto deste número pela densidade volúmica de massa do cobre:
A densidade volúmica de carga de condução é o produto de pela carga elétrica de cada carga de condução, a qual, neste caso, é igual à carga elementar :
Finalmente, a velocidade média dos eletrões de condução, usando a expressão (5.19), é:
O exemplo anterior mostra que os eletrões de condução num fio de cobre, com corrente de 1 A, têm uma velocidade média de poucos centímetros por hora. No entanto, há que ter em conta que apesar da velocidade ser tão baixa, num fio de vários metros, começará a fluir corrente elétrica num extremo do fio no mesmo instante em que começa a entrar corrente elétrica pelo extremo oposto. A situação é semelhante a uma mangueira, com muitos metros de comprimento, cheia de água; no instante em que é ligada a torneira começa a sair água pelo extremo oposto, porque a água que sai não teve de percorrer toda mangueira desde a torneira até ao outro extremo.
5.5 Potência elétrica
A figura 5.7 é o diagrama de circuito de um dispositivo passivo ligado a uma bateria ideal entre o ponto A, no elétrodo negativo da bateria, e o ponto B, no elétrodo positivo. O ponto A encontra-se a um potencial elétrico e o ponto B a um potencial , sendo . A bateria é dita ideal porque estamos a admitir que a diferença de potencial entre os pontos A e B, , é igual à f.e.m da bateria, , o que não acontece numa bateria real, como veremos adiante na secção 5.7.4.
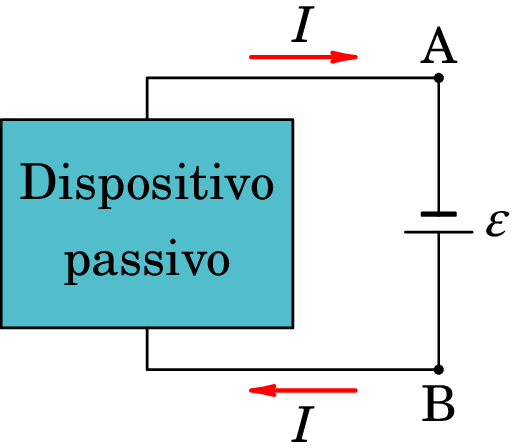
Pelo dispositivo circula uma corrente elétrica desde o ponto B até ao ponto A. Durante um intervalo de tempo sai carga positiva por B e entra a mesma carga por A. A energia elétrica desta carga no ponto B é (ver expressão (4.4)) e no ponto A é .
Como o potencial em B é maior do que em A, a variação da energia elétrica da carga quando esta circula pelo dispositivo é negativa. Portanto, durante o intervalo , a carga de condução perde energia potencial elétrica na passagem pelo dispositivo igual a:
| (5.25) |
Note-se que na expressão acima e . Esta energia perdida é dissipada e/ou convertida em outro tipo de energia no dispositivo. A energia dissipada neste caso é pois dada por:
| (5.26) |
A potência dissipada no dispositivo passivo, igual à energia dissipada por intervalo de tempo , é então dada por:
| (5.27) |
Por outro lado, na passagem de A para B pela bateria a carga ganha, no intervalo de tempo , uma energia e a potência fornecida à carga pela bateria ideal é então dada por:
| (5.28) |
Como a energia ganha pela carga provém da bateria, então a bateria perde uma energia , encontrando-se pois a descarregar. Uma vez que , vemos que a potência dissipada no dispositivo é igual à potência fornecida pela bateria, facto este que traduz o princípio da conservação da energia. Concluindo, a potência fornecida pela bateria ideal, proveniente de reações químicas, é convertida em outro tipo de energia (mecânica, lumínica, etc.) e/ou dissipada sob a forma de calor no dispositivo passivo.
A unidade de SI de potência, o watt (W), é então igual ao produto das unidades SI de corrente e potencial:
| (5.29) |
Exemplo 5.3
Num condutor, ligado a uma pilha ideal com f.e.m. de 1.5 V, circulam eletrões de condução durante 2 segundos. Calcule: (a) A corrente média; (b) A energia fornecida pela pilha durante esse intervalo; (c) A potência média fornecida pela pilha; (d) Sabe-se que a carga máxima da pilha é de 3 A·h e que esta se encontrava completamente carregada quando começou a fornecer os eletrões ao condutor. Se fosse possível manter a mesma corrente média até a pilha descarregar totalmente, quanto tempo demoraria a pilha a descarregar?
Resolução. (a) A carga transferida é o valor absoluto da carga dos eletrões:
e a corrente média é:
(b) A energia elétrica fornecida pela pilha nesse intervalo é,
(c) A potência média fornecida é igual a essa energia, dividida pelo intervalo de tempo:
ou alternativamente:
(d) Admitindo que a corrente fornecida pela pilha é constante no tempo, então a carga na pilha diminui linearmente em função do tempo:
A pilha descarrega totalmente para um tempo para o qual . Deste modo, o tempo é igual à carga máxima da pilha a dividir pela corrente média:
5.6 Curvas características voltagem-corrente
Como vimos, a potência elétrica dissipada num dispositivo passivo é igual ao produto da corrente vezes a diferença de potencial no dispositivo. As especificações de cada dispositivo costumam ser a sua voltagem (diferença de potencial à qual deverá ser ligado) e potência nominal, i.e. a potência que dissipará se a diferença de potencial for a indicada. Por exemplo, duas lâmpadas de 12V, com potências nominais de 1 W e de 2 W; as lâmpadas podem ser ligadas a uma diferença de potencial diferente da voltagem recomendada de 12 V, mas sempre que ambas sejam ligadas à mesma diferença de potencial, a corrente na lâmpada de 2 W será o dobro da corrente na lâmpada de 1 W.
A corrente correspondente a uma determinada diferença de potencial será diferente para diferentes dispositivos. Cada dispositivo tem uma curva característica que relaciona a sua corrente , com a diferença de potencial a que for ligada. A figura 5.8 mostra as curvas características de três dispositivos diferentes.
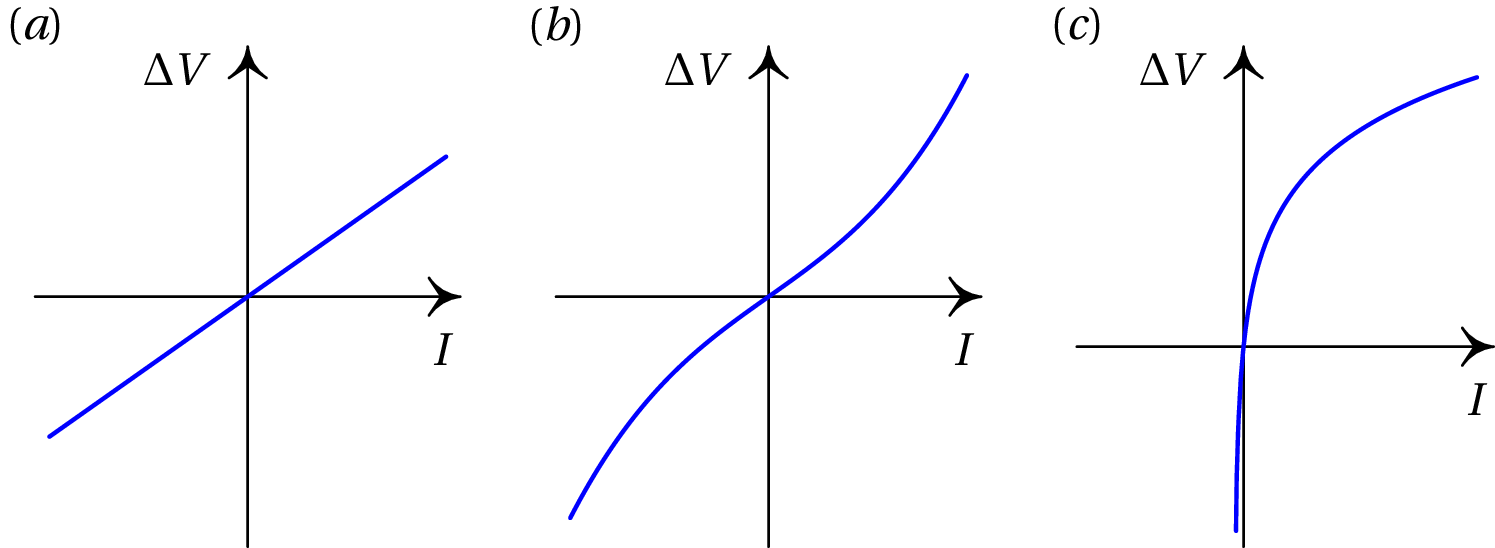
5.7 Resistência elétrica e lei de Ohm
Consideremos uma barra metálica homogénea, com secção transversal de área constante e comprimento , tal como mostra a figura 5.9 (não tem de ser retilínea, como na figura, enquanto tenha secção transversal de área constante tal como o fio da figura 5.5).
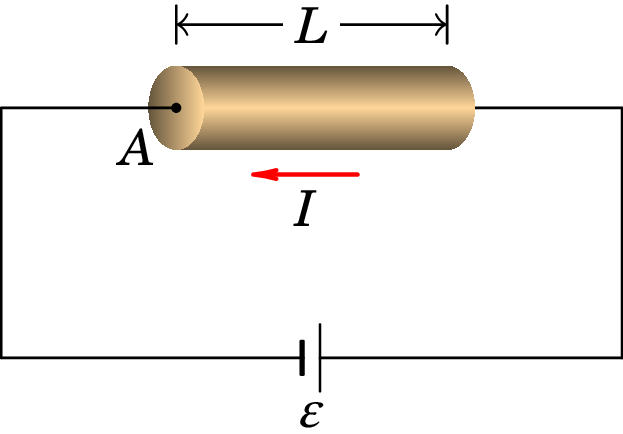
Nos metais e noutros condutores com uma nuvem densa de cargas de condução, a nuvem de condução é semelhante a um fluido incompressível. O movimento das cargas de condução através do condutor é contrariado por forças dissipativas de tipo viscoso devido à interação entre a nuvem de cargas de condução e a rede cristalina formada pelos iões positivos da barra metálica.
O lado esquerdo da figura 5.10 mostra a nuvem de eletrões de condução a deslocar-se com velocidade em relação à rede cristalina. No lado direito da figura, visto no referencial que se desloca com a nuvem de condução, os iões positivos deslocam-se através da nuvem de eletrões de condução com velocidade , comportando-se como esferas a caírem dentro de um líquido viscoso, por exemplo, a glicerina; neste caso, em vez da força gravítica, os iões são acelerados pelo campo elétrico dentro da barra.

A força dissipativa entre a nuvem de eletrões de condução e cada ião é tratada como sendo do tipo viscoso de Stokes, sendo portanto proporcional e contrária à velocidade relativa entre os iões e a nuvem de eletrões de condução. A força dissipativa tem pois módulo diretamente proporcional ao módulo da velocidade :
| (5.30) |
onde é uma constante característica de cada material.
O módulo da velocidade atinge um valor limite, (constante), quando a força dissipativa (5.30) é igual à força elétrica:
| (5.31) |
onde é a carga de cada ião e o módulo do campo elétrico dentro do condutor. A velocidade limite é designada por velocidade de condução.
A velocidade pode ser escrita em função da corrente e da área usando a equação (5.19), com densidade volúmica de carga de condução igual ao número de cargas de condução por unidade de volume, (ver exemplo 5.2), vezes a carga de cada uma dessas cargas: 11Observe-se que o valor absoluto da densidade volúmica de cargas de condução é igual à densidade volúmica de carga dos iões positivos. No lado direito da equação (5.31) o campo elétrico, uniforme, é igual à diferença de potencial no condutor, dividida pelo seu comprimento . Como tal, a equação (5.31) conduz a:
| (5.32) |
O primeiro termo entre parêntesis, é a denominada resistividade elétrica, a qual depende das propriedades físicas do material, sendo portanto uma característica de cada material, e identificá-la-emos pelo símbolo :
| (5.33) |
O segundo termo entre parêntesis da expressão (5.32) depende da forma geométrica do condutor e o seu produto com a resistividade é a denominada resistência elétrica do condutor:
| (5.34) |
Note-se que a resistência elétrica de um condutor depende do material condutor usado () e de fatores geométricos destes ( e ). Esta análise é análoga à efetuada anteriormente para a capacidade elétrica dos vários tipos de condensadores estudados.
A equação (5.32) é a lei de Ohm:
| (5.35) |
A diferença de potencial num condutor é diretamente proporcional à corrente elétrica através dele, sendo a constante de proporcionalidade a resistência elétrica do condutor.
A unidade usada para medir resistências no sistema internacional de unidades é o ohm representado pela letra grega (ómega maiúsculo). Uma resistência de 1 ohm é uma resistência em que uma voltagem de 1 volt produz uma corrente de 1 ampere:
| (5.36) |
Assim, a unidade SI da resistividade elétrica, , expressão (5.33), é .
A lei de Ohm é válida unicamente nos materiais condutores com forças dissipativas como as estudadas nesta secção, chamados condutores óhmicos. Um condutor óhmico designa-se simplesmente por resistência. A figura 5.11 mostra o símbolo usado para representar uma resistência num diagrama de circuito. A caraterística voltagem-corrente de uma resistência é uma reta que passa pela origem, como no gráfico (a) da figura 5.8, no qual o declive é o valor da resistência elétrica.
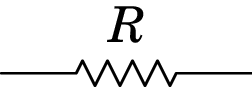
As forças dissipativas num condutor óhmico acarretam geração de calor, devido às vibrações da rede cristalina, fenómeno este designado por efeito Joule. Basicamente, o efeito Joule consiste na conversão de energia elétrica em calor. A energia elétrica perdida pela nuvem de eletrões de condução quando atravessa um condutor é absorvida pela rede cristalina, aumentando a energia das vibrações dos seus iões e portanto a temperatura do condutor, o qual dissipa depois energia sob a forma de calor.
O calor gerado é então igual à energia elétrica dissipada pelo condutor, cuja potência é dada pela expressão (5.27).
A lei de Ohm (5.35) permite escrever a potência dissipada numa resistência em função do seu valor:
| (5.37) |
onde se usou a expressão (5.27).
A lei de Ohm pode ser escrita também como a relação entre a densidade de corrente e o campo elétrico em cada ponto do material, combinando as equações (5.20) e (5.31):
| (5.38) |
A expressão (5.38) é por vezes designada por lei de Ohm microscópica e mostra que, para , o sentido do vector densidade de corrente elétrica, i.e., o sentido da corrente elétrica, é o mesmo que o sentido do campo elétrico, tal como discutido anteriormente na secção 5.3. Vemos também que a densidade de corrente elétrica é um campo vetorial, definido portanto em cada ponto do espaço e que as suas de linhas de campo possuem a forma e o sentido das linhas do campo elétrico no interior de um condutor óhmico
5.7.1 Condutores e dielétricos
Na prática, os materiais dielétricos não são isoladores perfeitos. Um isolador perfeito deveria ter uma resistividade infinita. A porcelana, usada em instalações elétricas por ser muito bom isolador, tem resistividade de aproximadamente ; valor este muito elevado em comparação com a resistividade dos metais (da ordem de ), mas não infinito.
Calculando a divergência nos dois lados da expressão (5.38) e usando a equação de continuidade (5.24) e a lei de Gauss num dielétrico (4.52), obtém-se uma equação diferencial para a densidade volúmica de carga livre em qualquer ponto dentro do material, em ordem ao tempo:
A constante , com unidades de tempo, é denominada por constante de tempo do material. Para um valor inicial da densidade de carga livre num ponto, se quiser, numa dada sub-região pequena de um material, a solução dessa equação diferencial é:
| (5.39) |
A carga livre diminui de forma exponencial (deslocando-se para a superfície do material) e o tempo de relaxação indica o quão rápido diminui a carga, ou por outras palavras, o quão rápido a carga se difunde pelo material. Nos metais, com susceptibilidade praticamente nula e constante dielétrica , o tempo de relaxação é da ordem de s. Num isolador este tempo pode ser da ordem de horas ou de dias.
5.7.2 Variação da resistência com a temperatura
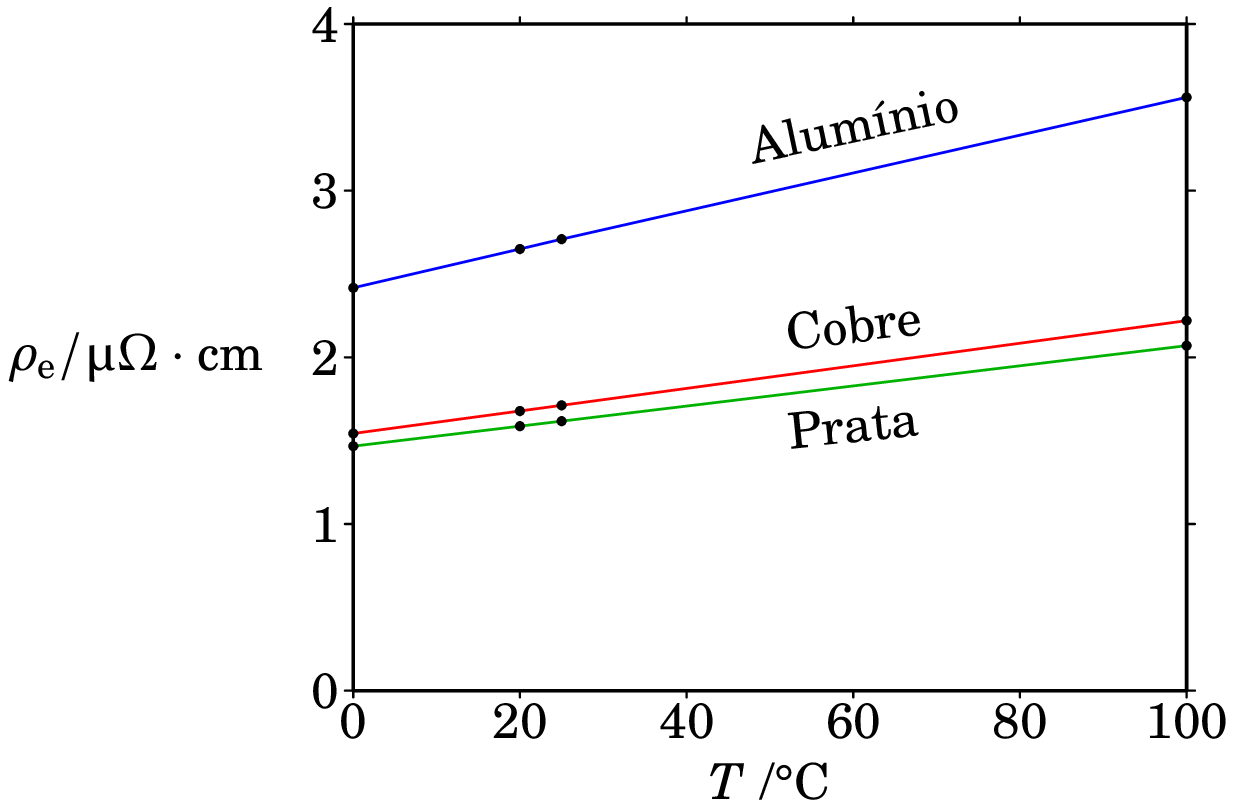
Nos metais e ligas metálicas, observa-se experimentalmente que a relação entre a resistividade e a temperatura é bastante linear a temperaturas entre °C e °C. A figura 5.12 mostra o gráfico dos valores medidos das resistividades do alumínio, cobre e prata a 0 °C, 20 °C, 25 °C e 100 °C.
Os dados experimentais de cada metal ou liga metálica podem então ser reproduzidos com apenas duas constantes, a saber, a resistividade elétrica à temperatura ambiente de 20 °C, , e o coeficiente de temperatura, . Com estas duas constantes, a resistividade em função da temperatura , em graus Celsius, é dada pela seguinte relação empírica:
| (5.40) |
Como o coeficiente de expansão linear/superficial dos condutores costuma ser muito menor do que o seu coeficiente de temperatura , costuma admitir-se que o fator na equação (5.34) permanece constante e a equação (5.40) conduz a:
| (5.41) |
onde é a resistência elétrica a 20 °C e é a resistência elétrica à temperatura , em graus Celsius.
A tabela 5.2 mostra os valores da resistividade e do coeficiente de temperatura dos metais e ligas metálicas mais usados para construir cabos para circuitos elétricos. O constantan é uma liga que tem a vantagem de ter resistividade quase constante e é usada na construção de termopares; o valor negativo do coeficiente de temperatura do constantan indica que a sua resistividade de facto diminui entre 0 e 100 °C, mas essa diminuição é muito pequena. A resistividade do níquel-crómio também não aumenta muito entre 0 e 100 °C, sendo muito usado para resistências de aquecimento, devido ao facto de suportar temperaturas muito elevadas. O tungsténio é o material que era usado nas lâmpadas incandescentes, nas quais a temperatura muito elevada fazia com que o metal emitisse luz amarela.
| Metal/ Liga | ||
| () | () | |
| Alumínio | 2.650 | |
| Latão (70% Cu, 30% Zn) | 6.08 | |
| Constantan (60% Cu, 40% Ni) | 45.38 | |
| Cobre | 1.678 | |
| Níquel-crómio (79% Ni, 21% Cr) | 107.5 | |
| Platina | 10.5 | |
| Prata | 1.587 | |
| Tungsténio | 5.28 |
(Fonte: Rumble 2023)
A equação (5.40) pode escrever-se como,
| (5.42) |
ficando assim mais claro que é dada pela equação de uma reta com declive e, como tal, apesar do declive ser constante, o valor do coeficiente de temperatura depende da temperatura escolhida como referência, neste caso 20 °C. Os dados da tabela 5.2 permitem calcular o declive da resistividade de cada material em função da temperatura em graus Celsius.
Exemplo 5.4
Um fio de cobre de raio 0.0815 cm e comprimento de 40 cm transporta uma corrente de 1 A. Calcule o campo elétrico dentro do fio e a diferença de potencial nos extremos, quando a temperatura for de 30 °C.
Resolução. A resistividade no fio calcula-se usando os valores para o cobre (tabela 5.2)
a resistência do fio é
A diferença de potencial obtém-se a partir da lei de Ohm:
Como a secção transvesal do fio é constante, o módulo do campo elétrico também deve ser constante e, portanto, pode ser calculado através da expressão para o campo elétrico médio
5.7.3 Supercondutividade
Em 1911, o físico holandês Heike Kamerlingh Onnes (1853-1926) descobriu que a resistividade de alguns condutores diminui drasticamente quando a temperatura se aproxima do zero absoluto ( °C). A figura 5.13 mostra o gráfico original publicado por Kamerlingh Onnes em 1911, quando observou que a uma temperatura absoluta de 4.2 K (aproximadamente °C), a resistência do mercúrio diminui bruscamente 4 ordens de grandeza. Essa temperatura de 4.2 K é chamada temperatura crítica, do mercúrio. Este fenómeno chama-se supercondutividade, e os materiais que apresentam este comportamento são conhecidos como supercondutores.
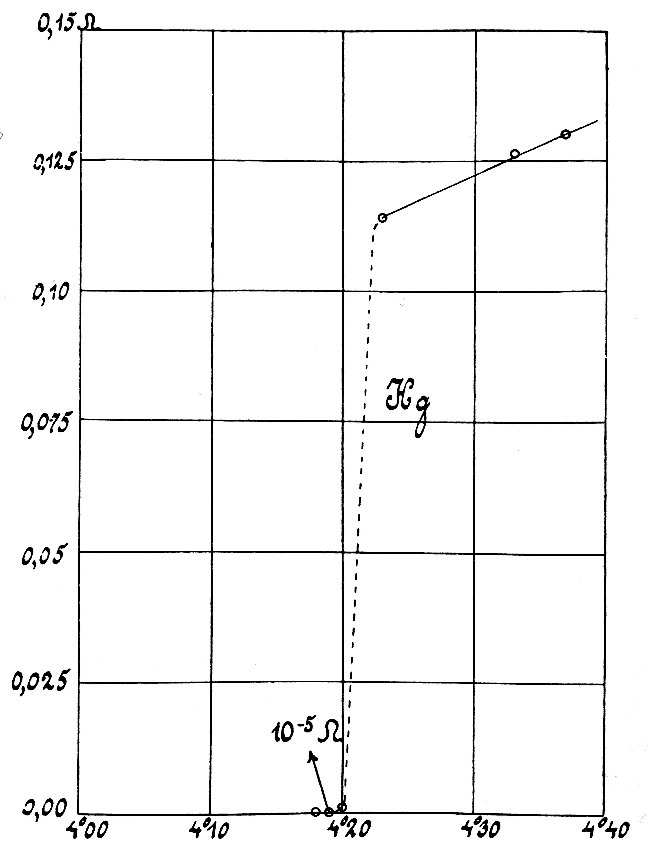
A supercondutividade, inicialmente vista como uma curiosidade, começou a atrair a atenção da comunidade científica com a sua descoberta em vários elementos metálicos (tais como alumínio, estanho, vanádio, chumbo, nióbio), mas sempre com temperaturas críticas abaixo de K, bem como em compostos metálicos, em particular, o boreto de magnésio possui temperatura crítica K, a mais alta até ao momento para um supercondutor do tipo metálico à pressão atmosférica.
A compreensão do mecanismo físico responsável pela supercondutividade de tipo metálico permaneceu um desafio teórico durante várias décadas. Em 1957, o engenheiro eletrotécnico norte-americano John Bardeen e os físicos norte-americanos Leon Cooper e Robert Schrieffer explicam o fenómeno da supercondutividade nos supercondutores metálicos.
A sua teoria (de base quântica), conhecida por Teoria BCS (iniciais dos seus autores), prevê essencialmente um estado supercondutor devido ao emparelhamento de dois eletrões nos denominados pares de Cooper. Este emparelhamento é devido à interação dos eletrões com a rede de iões do metal. Curiosamente, a rede de iões que se comporta como um obstáculo à passagem da corrente elétrica num material condutor ou isolador, revela-se como essencial para que ocorra supercondutividade do tipo metálico. A supercondutividade é pois um fenómeno quântico à escala macroscópica.
Durante muito tempo, as aplicações práticas da supercondutividade eram bastante limitadas, devido às temperaturas críticas serem difíceis de obter por serem muito baixas. Contudo, durante a década de 1980 e até ao presente vários novos materiais foram descobertos, nos quais a temperatura crítica é muito mais elevada, sendo possível obtê-la usando azoto líquido, abrindo-se assim a possibilidade de múltiplas aplicações práticas.
Os físicos experimentais suíços Alex Müller e Jorg Bednorz observam em 1986 que o cuprato de lantânio , um material cerâmico isolador do ponto de vista elétrico, quando dopado com Bário, (onde denota a concentração de dopagem), torna-se supercondutor à temperatura crítica K para uma dopagem óptima de , descobrindo o primeiro supercondutor de alta-temperatura.
Após esta descoberta, vários supercondutores cerâmicos de alta-temperatura à base de cuprato foram sendo descobertos. A sigla HTS (High-Temperature Superconductors) denonima esta classe de supercondutores. De referir a descoberta em 1987 que o composto de cuprato possui uma temperatura crítica K para uma dopagem óptima de , sendo o primeiro supercondutor a superar a temperatura de liquefacção do azoto (77 K). O cuprato , descoberto em 1993, possui K e é atualmente o HTS com a mais elevada temperatura crítica à pressão atmosférica.
De referir, que do ponto de vista da rede cristalina estes materiais, grosso modo, são constituídos por planos de óxido de cobre, intercalados com os restantes elementos. Enquanto que a condução elétrica nos supercondutores metálicos de baixa temperatura é tridimensional, movendo-se os electrões por toda a rede, nos supercondutores de alta-temperatura, a condução elétrica é bidimensional, movendo-se os electrões nos planos de óxido de cobre, o que faz com que a interação coulombiana eletrão-eletrão desempenhe um papel preponderante, originando fortes correlações eletrónicas. Apesar de inúmeros trabalhos experimentais e teóricos sobre os HTS, presentemente ainda não existe uma teoria bem estabelecida que explique o mecanismo físico responsável pela sua supercondutividade.
Refira-se ainda que nos supercondutores do tipo metálico e nos HTS é possível obter temperaturas críticas mais elevadas quando estes são sujeitos a altas pressões (por exemplo, o possui K C à pressão de GPa, uma pressão cerca de vezes maior do que a pressão atmosférica).
5.7.4 Resistência interna de uma bateria
No modo normal de funcionamento das baterias ou pilhas, em que a corrente entra na bateria pelo elétrodo negativo e sai pelo elétrodo positivo, a energia elétrica das cargas de condução aumenta quando passam pela bateria, i.e, a bateria fornece energia elétrica e diz-se que funciona como gerador, pois gera energia elétrica. As reações químicas no eletrólito fornecem potência elétrica . Uma parte dessa potência é dissipada em calor dentro da própria bateria, devido à passagem das cargas pelos elétrodos e pelo eletrólito. Se os elétrodos e o eletrólito forem condutores ohmicos, com resistência total , a potência dissipada em calor dentro da bateria é e, como tal, a potência fornecida pela bateria ao dispositivo ligado entre os elétrodos é . Como esta potência fornecida ao dispositivo é igual a , obtém-se então a expressão da caraterística da bateria, no modo normal em que fornece energia a um dispositivo:
| (5.43) |
A figura 5.14 mostra a caraterística do gerador. A ordenada na origem é o valor da f.e.m. e o valor absoluto do declive é a resistência interna da bateria, . A corrente é a corrente máxima que pode fornecer a bateria, quando for ligada em curto-circuito (diferença de potencial nula entre os elétrodos).
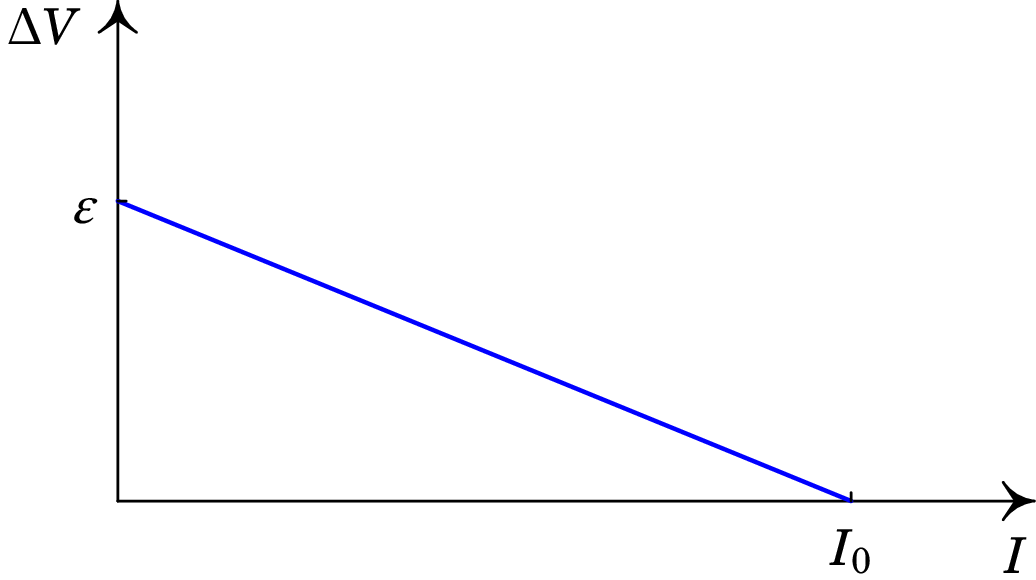
Nas baterias recarregáveis, o sentido normal da corrente pode ser invertido, ligando outra fonte externa com f.e.m. maior que a da bateria e contrariando a sua polaridade. Nesse caso, a corrente entra na bateria pelo elétrodo positivo e sai pelo elétrodo negativo. As cargas de condução perdem energia elétrica durante a sua passagem pela bateria. A bateria está então a absorver potência elétrica , que está a ser fornecida pela fonte externa. A bateria passa a funcionar como recetor, pois recebe energia elétrica. Uma parte dessa potência absorvida é usada para inverter as reações químicas no eletrólito, aumentando o número de catiões e aniões; essa parte é igual . A outra parte da potência absorvida pela bateria é dissipada em calor na resistência interna e é igual a . Como tal, a caraterística da bateria, no modo recetor, é
| (5.44) |
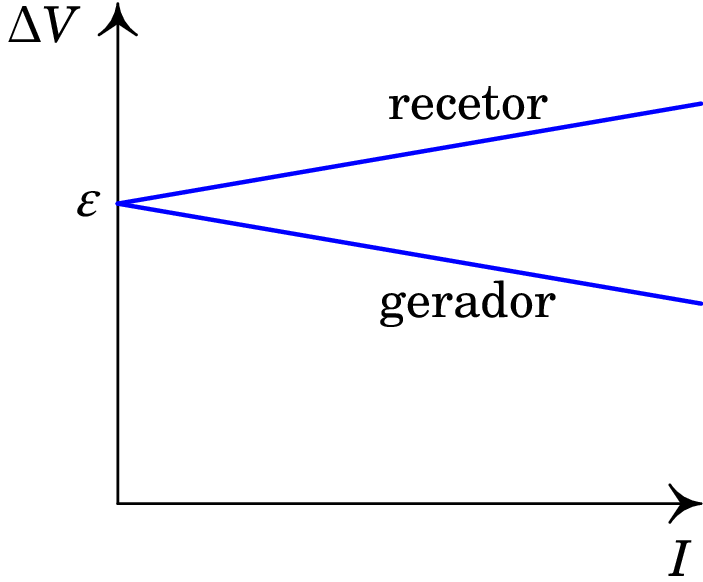
A figura 5.15 mostra as caraterísticas da bateria nos dois modos de funcionamento. Nos dois casos, o valor absoluto do declive é igual à resistência interna . A voltagem da bateria, , só é igual ao valor da sua f.e.m., , quando a bateria não está ligada a nenhum dispositivo (corrente nula) — por outras palavras, a f.e.m. de uma bateria é igual à diferença de potencial entre os seus terminais em circuito aberto.
Quando a bateria é ligada a um dispositivo, passando corrente através dela, a voltagem da bateria é maior que a f.e.m. no modo recetor e menor que a f.e.m. no modo gerador. No modo gerador, quando a bateria está em curto-circuito (ligam-se os dois terminais da bateria entre si), a voltagem diminui para zero, e toda a energia fornecida pelas reações químicas é dissipada em calor dentro da própria bateria, descarregando-se totalmente, se antes não se queimar pelo calor dissipado.
O diagrama de circuito correspondente deve incluir uma fonte ideal de f.e.m. ligada em série a uma resistência , tal como na figura 5.16, em que a bateria é todo o conjunto entre os pontos P (elétrodo positivo) e N (elétrodo negativo); as duas partes do diagrama de circuito da bateria, fonte ideal de f.e.m. e resistência interna , representam as reações químicas no eletrólito e geração de calor por efeito Joule dentro da própria bateria.
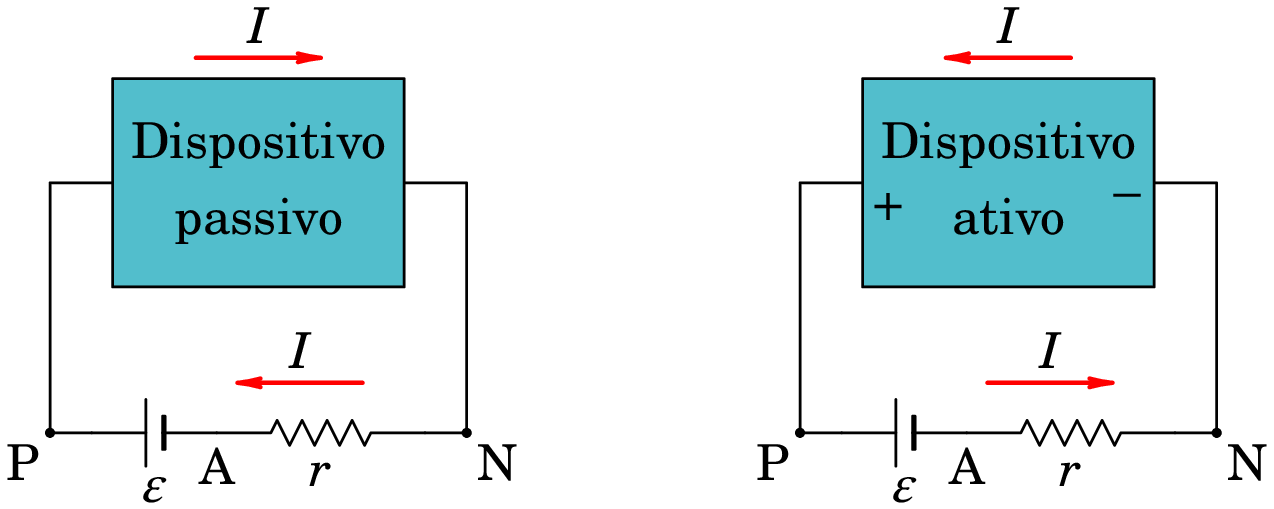
O calor libertado por efeito Joule implica sempre potência elétrica dissipada, qualquer que seja o modo de funcionamento da bateria. As reações químicas fornecem energia elétrica no modo gerador e absorvem energia elétrica no modo recetor. No lado esquerdo da figura 5.16 a bateria está ligada a um dispositivo passivo, em que a bateria funciona sempre como gerador, e no lado direito da figura está ligada a um dispositivo ativo, em que pode trabalhar como gerador ou como recetor; se o dispositivo ativo incluir uma fonte de f.e.m. maior do que a da bateria e estiver ligada como indicado na figura, a bateria passa a trabalhar como recetor.
No lado esquerdo da figura 5.16, o diagrama da fonte ideal de f.e.m. mostra que o potencial do elétrodo positivo é maior do que o potencial do ponto intermédio A, e a diferença de potencial entre eles é . O sentido da corrente na resistência interna mostra que o potencial do elétrodo negativo é maior do que e, pela lei de Ohm, a diferença de potencial entre eles é . A voltagem nos elétrodos da bateria é então:
| (5.45) |
e confere-se que o circuito corresponde à curva característica (5.43) do modo gerador.
No lado direito da figura 5.16, note-se que o potencial do elétrodo positivo P continua a ser maior do que o potencial do ponto intermédio A, pelo que a diferença entre estes dois pontos é sempre dada por , e que o sentido da corrente na resistência interna mostra que agora é menor do que , sendo a diferença entre eles . Assim, a voltagem nos elétrodos da bateria é neste caso dada por:
| (5.46) |
e confere-se que o circuito corresponde à curva característica (5.44) do modo recetor.
5.8 Associações de resistências
A curva caraterística voltagem-corrente de um conjunto de várias resistências tem sempre o aspecto da característica de uma única resistência; nomeadamente, é uma reta que passa pela origem. O declive dessa reta é a resistência equivalente. Podem-se usar algumas regras simples para calcular a resistência equivalente, quando as resistências estão ligadas em série ou em paralelo.
Várias resistências , , …, estão ligadas em série, quando cada uma de elas está a seguir à anterior, de modo que a corrente que passa por cada uma delas é a mesma, como mostra a figura 5.17.

A diferença de potencial no sistema é a soma das diferenças de potencial em cada uma das resistência, e como a corrente é igual em todas elas, obtém-se:
| (5.47) |
Como tal, o sistema é equivalente a uma única resistência com valor igual à soma das resistências.
| (5.48) |
Diz-se que resistências , , …, estão ligadas em paralelo, quando cada uma delas estiver ligada entre dois pontos comuns a todas elas, de tal modo que a diferença de potencial em cada uma delas é a mesma, tal como na figura figura 5.18.
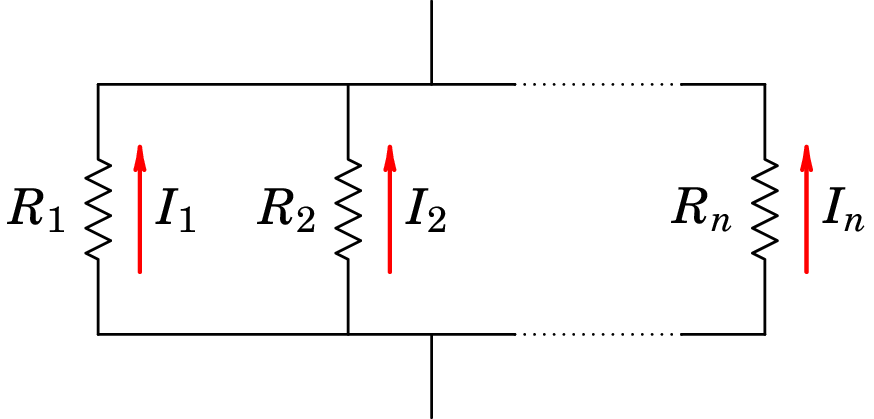
A diferença de potencial, , é a mesma em todas as resistências e a corrente no sistema é a soma das correntes em cada resistência:
| (5.49) |
O sistema é então equivalente a uma única resistência que verifica a equação
| (5.50) |
No caso particular em que há apenas duas resistências, esta equação pode ser escrita também da forma seguinte:
| (5.51) |
É possível simplificar alguns sistemas com várias resistências, substituindo sucessivamente as resistências que se encontram em série ou em paralelo por uma resistência equivalente, até obter uma única resistência equivalente.
Exemplo 5.5
No circuito da figura, calcule a corrente através de cada uma das resistências, para uma diferença de potencial igual a 12 V.
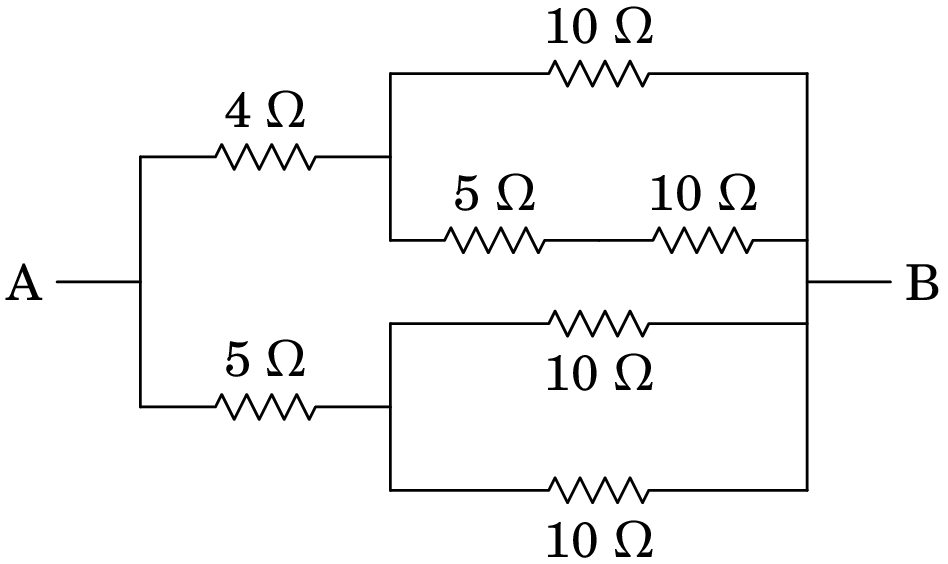
Resolução. Substituindo sucessivamente as resistências ligadas em série ou em paralelo, pode simplificar-se o circuito entre A e B em 3 passos:
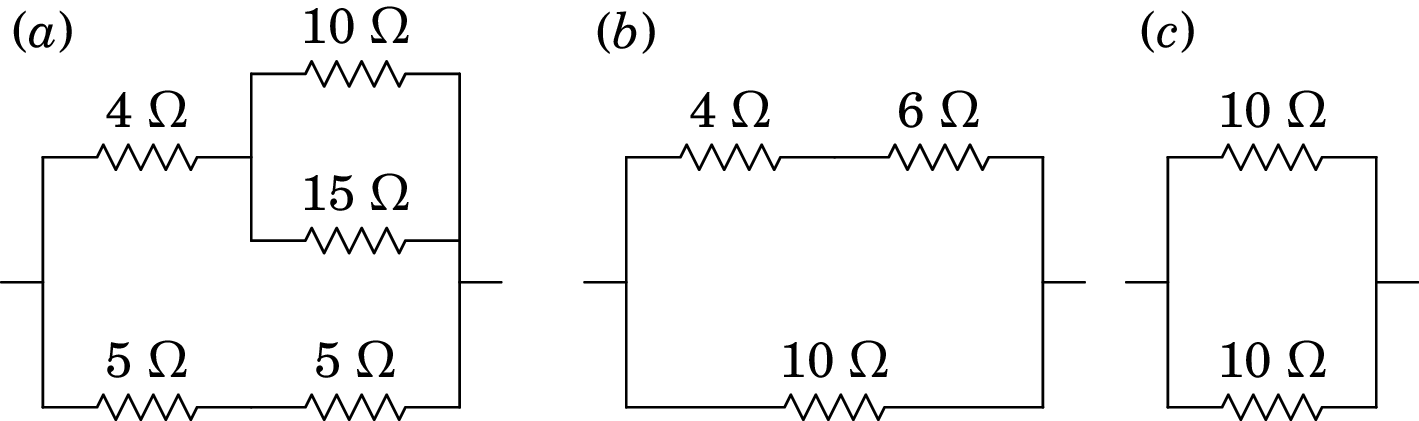
Note-se que não é necessário reduzir o circuito até ficar com uma única resistência equivalente, pois no passo (c) já se podem calcular as correntes correspondentes a uma diferença de potencial de 12 V em cada resistência; a corrente é 12/10 = 1.2 A através de cada uma delas.
Uma vez calculadas as correntes e diferenças de potencial em (c), pode-se resolver o circuito da figura (b): nas 3 resistências a corrente é neste caso igual a 1.2 A, pelo que a diferença de potencial na resistência de 6 é 61.2 = 7.2 V.
A seguir procede-se a analisar o circuito da figura (a); a corrente nas resistências de 4 e 5 é a calculada em (b), nomeadamente, 1.2 A. Nas resistências de 10 e 15 a diferença de potencial é 7.2 V, conforme cálculo feito para a resistência equivalente em paralelo. As correntes nessas duas resistências são então:
Finalmente, no circuito original, a corrente na série de resistências de 5 e 10 é igual a , enquanto a corrente nas duas resistências de 10 em paralelo é distribuída por igual, passando 0.6 A por cada resistência.
Resumindo, no ponto A entra uma corrente total de 2.4 A, passando 1.2 A pelas resistências de 4 e 5 . Ao ponto B chegam quatro correntes: uma corrente de 0.72 A da resistência de 10 na parte superior, uma corrente de 0.48 A que percorre as resistências de 10 e 5 em série e duas correntes de 0.6 A que passam por cada uma das resistências de 10 em paralelo. A corrente total que sai em B é 2.4 A.
Problemas
-
5.1.
Determine o trabalho realizado por uma pilha de 9 V, que fornece uma corrente de 235 mA durante 5 minutos.
-
5.2.
Uma certa bateria de automóvel tem carga máxima de 250 Ah, que corresponde à carga disponível quando está carregada a 100%.
(a) Depois de algum uso, a bateria descarrega até 60% da sua carga máxima. Qual é a carga, em coulomb, com que fica a bateria?
(b) A seguir, a bateria liga-se a um carregador de 12 V para a recarregar e observa-se que inicialmente a corrente do carregador tem intensidade de 7 A, mas 6 horas depois diminui a 3 A. Admitindo diminuição linear da corrente em ordem ao tempo, com que percentagem da sua carga máxima fica a bateria no fim das 6 horas? -
5.3.
A corrente num cabo varia de acordo com a função , onde mede-se em miliampere e em segundos.
(a) Que carga transporta o cabo desde até s?
(b) Qual o valor da corrente constante que transporta a mesma quantidade de carga no mesmo intervalo de tempo? -
5.4.
Num condutor ligado a uma pilha com f.e.m. de 1.5 V, circulam eletrões de condução durante 2 horas. Determine:
(a) A intensidade da corrente média.
(b) A energia fornecida pela pilha durante esse intervalo.
(c) A potência média fornecida pela pilha.
(d) Se a carga inical da pilha era de 3 A·h, com que carga fica após as 2 horas? -
5.5.
No circuito da figura, determine a resistência equivalente:
(a) entre B e D,
(b) entre A e B,
(c) entre A e D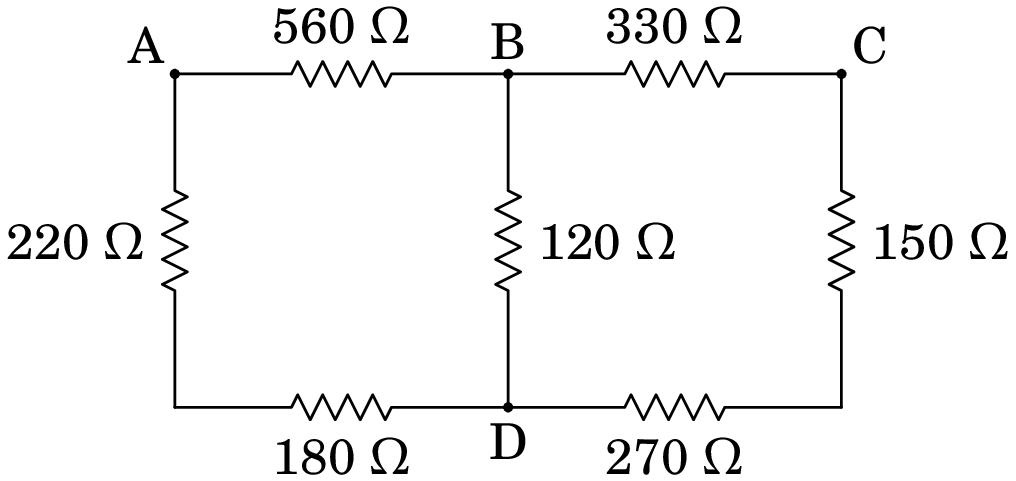
-
5.6.
Determine a corrente e a diferença de potencial em cada resistência:
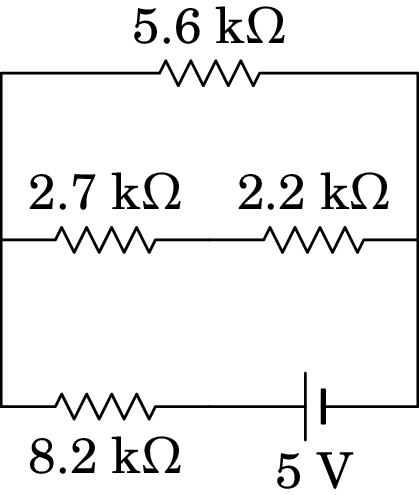
-
5.7.
A temperatura num dado momento é 12 °C. Quanto deve aumentar a temperatura para que a resistência de um fio de cobre aumente 10%?
-
5.8.
A resistência de uma lâmpada incandescente de 60 W e 230 V, cujo filamento é feito de tungsténio, medida à temperatura ambiente de 20 °C é . No entanto, as especificações do fabricante (60 W e 230 V) conduzem a um valor muito mais elevado da resistência. Justifique esta diferença e calcule a temperatura do filamento de tungsténio quando a lâmpada se encontra acesa, assumindo que a resistividade elétrica do tungsténio varia linearmente com a temperatura.
-
5.9.
Para manter a temperatura a 20 °C num quarto, durante um dia de inverno, estima-se ser necessária energia de 132 kJ cada minuto. Se essa energia for fornecida por um aquecedor elétrico, ligado à tensão de 220 V disponível na casa:
(a) Determine a intensidade da corrente no aquecedor.
(b) Se o custo da energia elétrica for de 12 cêntimos por kw·h, qual o custo de manter ligado o aquecedor durante 10 minutos? -
5.10.
Uma bateria tem f.e.m. e resistência interna .
(a) Determine o valor da resistência de um circuito que, quando for ligado a essa bateria, consiga absorver a máxima potência possível (Sugestão: escreva a expressão da potência dissipada em em função de e , derive em ordem a e iguale a zero).
(b) Calcule o valor da potência máxima que a bateria pode fornecer a um circuito, em função de e . -
5.11.
Mostre que a constante de tempo, , tem unidades de tempo e calcule o tempo de relaxação do cobre.
-
5.12.
Um fio condutor de 1 m de comprimento tem uma resistência de 0.3 . O fio é esticado até o seu comprimento aumentar para 2 m. Qual será o novo valor da resistência?
-
5.13.
A diferença de potencial entre os elétrodos de uma bateria é 3 V quando a bateria é percorrida por uma corrente de 4 A, no sentido do elétrodo negativo para o positivo. Quando a corrente é de 2 A, no sentido oposto, a diferença de potencial aumenta até 12 V.
(a) Calcule a resistência interna da bateria.
(b) Qual é a f.e.m. da bateria? -
5.14.
No circuito representado na figura, mediu-se a corrente na resistência de 8 k obtendo-se o valor de 2 mA. Use esses dados para calcular o valor da f.e.m. da fonte e a diferença de potencial em cada resistência.
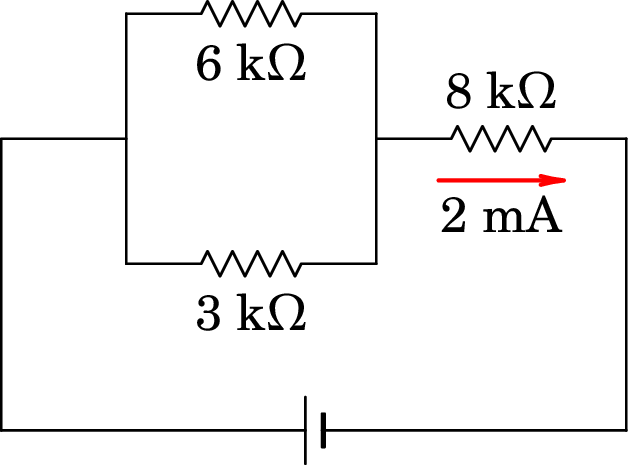
-
5.15.
Determine a corrente máxima que pode fornecer uma pilha com f.e.m. de 1.5 V e resistência interna de 0.2 , bem como a potência dissipada em calor dentro da própria pilha quando esta fornece a corrente máxima.
-
5.16.
No circuito da figura, determine a potência dissipada em cada resistência e a potência fornecida pela fonte de f.e.m.. Verifique que a potência fornecida pela fonte de f.e.m. é igual à soma das potências dissipadas em todas as resistências.
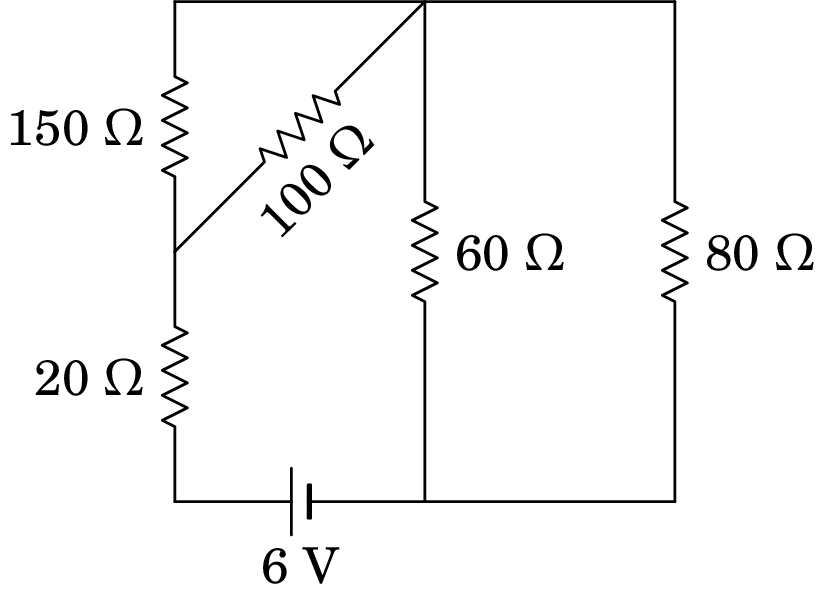
-
5.17.
Um fio condutor de cobre de 1.29 mm de diâmetro e revestido a borracha pode suportar, com segurança, uma corrente máxima de 6 A.
(a) Qual é a diferença de potencial que pode ser aplicada a 40 m deste fio? (admita temperatura ambiente, igual a 20 °C.)
(b) Calcule a potência dissipada no fio quando a corrente for igual à corrente máxima. -
5.18.
Um fio de níquel-crómio de 1.8 mm de diâmetro vai ser usado como aquecedor numa caldeira de água que produz 8 g de vapor de água por segundo. A fonte de alimentação fornece voltagem contínua de 220 V. Calcule o comprimento que deve ter o fio. (O calor de evaporação da água é 2257.2 J/g, e use 100 °C para a temperatura de ebulição da água.)
Respostas
-
5.1.
634.5 J.
-
5.2.
(a) C. (b) 72%.
-
5.3.
(a) 1.2 C. (b) 120 mA.
-
5.4.
(a) 214 mA. (b) 2.307 kJ. (c) 320 mW. (d) 2.573 A·h.
-
5.5.
(a) 93.39 . (b) 265.1 . (c) 249.5 .
-
5.6.
Na resistência de 5.6 k, 1.21 V e 216 µA. Na resistência de 2.7 k, 0.67 V e 246 µA. Na resistência de 2.2 k, 0.54 V e 246 µA. Na resistência de 8.2 k, 3.79 V e 462 µA.
-
5.7.
24.0 °C (i.e, a temperatura final é 36.0 °C).
-
5.8.
Quando a lâmpada está acesa, a temperatura do filamento de tungsténio é muito mais elevada do que a temperatura ambiente e, portanto, a resistência também é muito mais elevada. A temperatura do filamento é da ordem de 2822 °C.
-
5.9.
(a) 10 A. (b) 4.4 cêntimos.
-
5.10.
(a) . (b) .
-
5.11.
Em unidades SI, tem unidades de F/m (inverso das unidades de ) e tem unidades de . Como F é C/V e é V/A, as unidades de são C/A que é segundo. .
-
5.12.
1.2 .
-
5.13.
(a) 1.5 . (b) 9 V.
-
5.14.
V. Nas resistências de 3 k e 6 k, V; na resistência de 8 k, V.
-
5.15.
7.5 A e 11.25 W.
-
5.16.
Na resistência de 20 , 55.1 mW. Na resistência de 100 , 99.2 mW. Na resistência de 150 , 66.2 mW. Na resistência de 60 , 54.0 mW. Na resistência de 80 , 40.5 mW. A fonte de f.e.m. fornece 315 mW.
-
5.17.
(a) 3.08 V. (b) 18.5 W.
-
5.18.
6.30 m.