10. Circuitos de corrente alternada

Nikola Tesla (1856–1943)
No fim da década de 1880 viveu-se nos Estados Unidos da América um período conhecido como Guerra das Correntes. Nessa época já existia uma rede elétrica pública, de corrente contínua, usada principalmente para alimentar lâmpadas incandescentes e motores elétricos. A exploração dessa rede elétrica revertia grandes lucros a Thomas Alva Edison (1847–1931). Outras pessoas tentaram entrar nesse novo negócio milionário com as suas inovações; George Westinghouse (1846–1914) contratou Tesla, um jovem brilhante imigrante da Croácia, quem tinha inventado geradores de corrente alternada. A guerra das correntes acabaria por ser ganha pelo sistema de corrente alternada de Tesla e Westinghouse. Uma das principais vantagens sobre o sistema de corrente contínua de Edison é que permite transmitir eletricidade a grandes voltagens, diminuindo as perdas por efeito de Joule na transmissão, sendo depois convertida, por meio de transformadores, em voltagens menores, mais seguras, para uso industrial e doméstico.
10.1 Circuito LC
Um circuito com um indutor ligado em série a um condensador, denominado circuito LC, é um exemplo em que a corrente e a tensão oscilam em função do tempo. Num circuito LC ideal, sem resistência, essas oscilações mantêm a sua amplitude constante.
No circuito do lado esquerdo da figura 10.1, o interruptor está fechado (há muito tempo) e o interruptor aberto. Num instante, , abre-se o interruptor e, simultaneamente, fecha-se o interruptor . Assim, em o circuito equivalente é o circuito LC ideal no lado direito da figura 10.1.
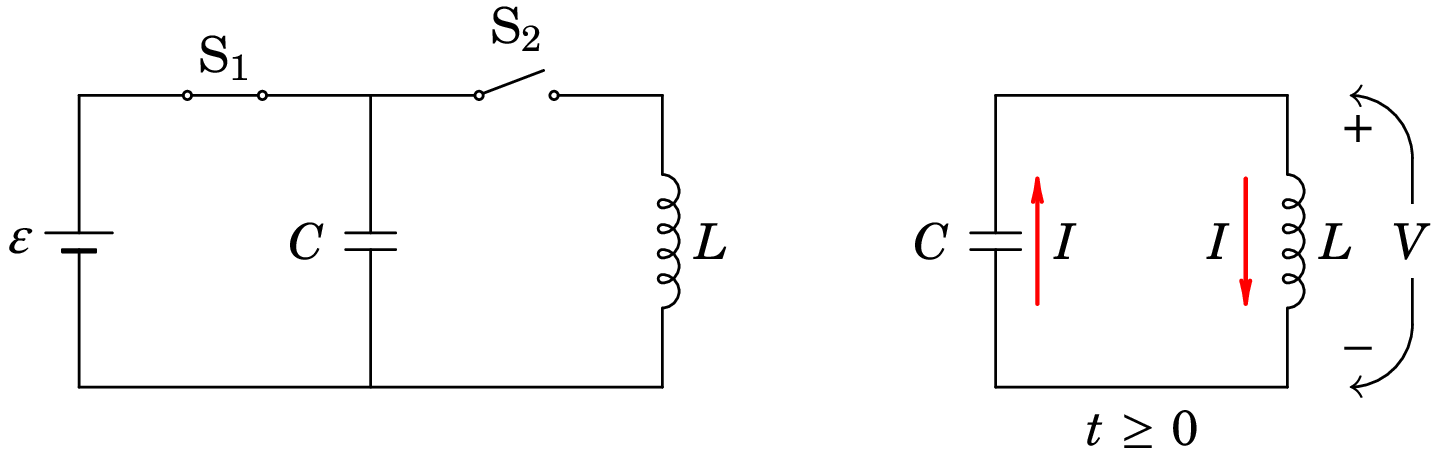
Consideremos que para , a fonte esteve ligada durante um tempo suficiente para que o condensador atingisse o seu estado estacionário. Para , veremos que a tensão no condensador variará no tempo: . A tensão inicial no condensador, em , é , e nesse instante a sua derivada em ordem ao tempo é nula: , porque o condensador está em estado estacionário.
Como mostra a equação (6.28), a corrente no condensador é diretamente proporcional à derivada da tensão nos seus terminais, a saber, . Mas, a forma como foram definidos os sentidos positivos de e de na figura 10.1, implica que o condensador funciona como um dispositivo ativo e o indutor como um dispositivo passivo, pelo que a corrente no circuito é:
| (10.1) |
e como a derivada de é nula em , a corrente inicial também é nula.
A relação entre a corrente e a tensão no indutor é dada pela equação (9.19):
| (10.2) |
Substituindo a equação (10.1) em (10.2) obtém-se a equação diferencial para a tensão:
| (10.3) |
onde,
| (10.4) |
é uma constante com unidades de frequência (como veremos, é uma frequência angular, dita frequência angular natural de um circuito LC).
A equação (10.3) é a equação de um oscilador harmónico simples, que já resolvemos na secção 7.2.1. é uma função que derivada duas vezes em ordem a dá a mesma função multiplicada por . As duas funções com essa propriedade são o seno e cosseno de . deverá ser então uma combinação linear dessas duas funções:
| (10.5) |
As condições iniciais em , e permitem calcular as constantes, obtendo-se que e . A tensão em função do tempo é então,
| (10.6) |
E a corrente no circuito em função do tempo, obtém-se a partir da equação (10.1):
| (10.7) |
onde,
| (10.8) |
Como tal, a corrente e a tensão oscilam com frequência , desfasadas de 90, de forma que quando uma delas é nula, a outra tem o seu valor máximo ou mínimo (figura 10.2).
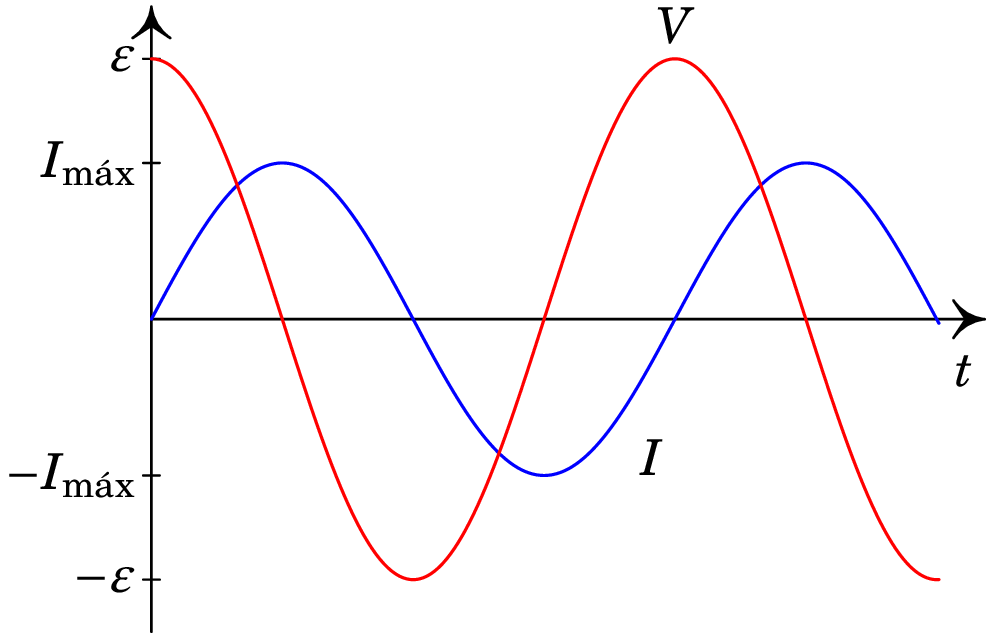
Vemos portanto que considerando o indutor como elemento passivo num circuito LC, então e , pelo que a corrente está atrasada de 90 em relação à tensão (ou, equivalentemente, a tensão está adiantada de 90 em relação à corrente).
Alternativamente, considerando o condensador como sendo o elemento passivo num circuito LC, o sentido da corrente no circuito da direita da figura 10.1 teria de ser invertido. Deste modo, e , pelo que a corrente estaria adiantada de 90 em relação à tensão ou, equivalentemente, a tensão estaria atrasada de 90 em relação à corrente.
Independentemente da escolha arbitrada, a corrente e a tensão num circuito LC, estão portanto desfasadas de 90, como referido anteriormente.
A tensão (10.6) e a corrente (10.7) são dois exemplos de funções alternadas: funções sinusoidais que oscilam entre um valor máximo e um valor mínimo, igual ao simétrico do valor máximo, com valor médio igual a zero. Outro exemplo de função alternada é a tensão produzida por um alternador (exemplo 9.3).
10.2 Tensão alternada
A figura 10.3 mostra a forma geral de uma função alternada . A função é caraterizada por 3 parâmetros: , e . é o valor máximo ou amplitude da função; o período é o intervalo de tempo entre dois máximos ou dois mínimos consecutivos e é o instante mais próximo de em que a função atinge o seu valor máximo.
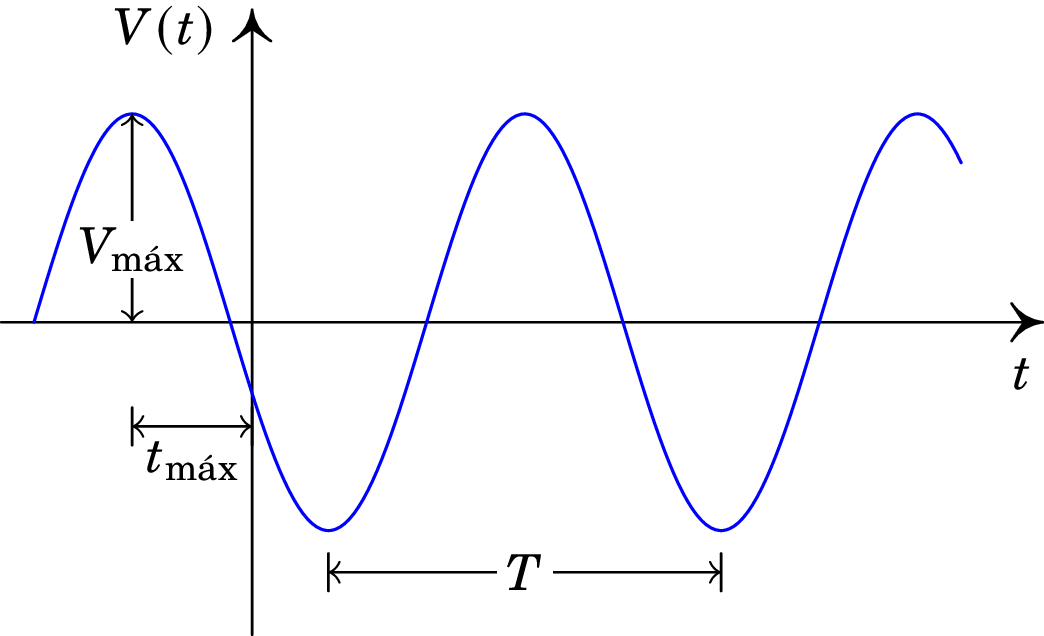
A frequência , ou número de oscilações por unidade de tempo, é o inverso do período () e a frequência angular é definida por:
| (10.9) |
Define-se também a fase inicial:11A fase inicial é positiva no caso da figura 10.3
| (10.10) |
Em vez do período e o tempo podemos caraterizar a função pela sua frequência angular e a sua fase inicial :
| (10.11) |
Note-se que é possível representar a mesma função de várias formas. Pode-se substituir o cosseno por seno e subtrair à fase inicial, sem alterar o resultado. Pode-se também inverter os sinais da frequência angular e da fase inicial, simultaneamente, e ainda somar ou subtrair qualquer múltiplo de à fase inicial. No entanto, para facilitar a caraterização dessas funções, usaremos apenas a função cosseno, frequências angulares positivas e fase inicial no intervalo . A fase inicial também pode ser arbitrada igual a zero se definirmos o instante quando a tensão tem o seu valor máximo. Basta então saber o valor máximo e a frequência angular da tensão alternada.
Nos diagramas de circuito, uma fonte ideal de tensão alternada representa-se pelo símbolo indicado na figura 10.4. Junto do símbolo costuma indicar-se a tensão máxima e a frequência . Os valores apresentados na figura são os usados na rede elétrica pública da União Europeia: frequência de 50 Hz e tensão máxima de 325 V.
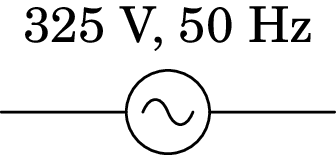
Num circuito com uma fonte de tensão alternada ligada a resistências, condensadores e indutores, a lei de Ohm (5.35), a equação (6.28) para os condensadores e a a equação (9.19) para os indutores garantem que a tensão e a corrente em todos esses dispositivos serão também funções sinusoidais com a mesma frequência angular da fonte, mas com diferentes valores máximos e diferentes fases iniciais.
Como se mostra no apêndice B, qualquer uma dessas tensões ou correntes pode ser representada por um fasor, que é um número complexo com módulo igual ao valor máximo da função e argumento igual à fase inicial da função. Por exemplo, os fasores da tensão e da corrente do circuito LC da secção anterior, mostrados na figura 10.2, são os seguintes:
| (10.12) |
As respetivas funções sinusoidais obtêm-se facilmente a partir do fasor, multiplicando o seu módulo pelo cosseno de mais o seu argumento em radianos (note-se que é igual a ). Para somar correntes ou tensões no circuito, basta somar os respetivos fasores.
Exemplo 10.1
Num nó de um circuito de corrente alternada entram duas correntes e saem outras duas correntes. Sabendo que as expressões das correntes que entram são e , e uma das correntes que sai é , calcule a outra corrente que sai, indicando o seu valor máximo e a sua fase inicial.
Resolução. Em termos matemáticos, usando a lei dos nós de Kirchhoff, expressão (6.5), o que está a ser pedido é o cálculo de
de forma a obter uma única função cosseno.
Comecemos por escrever os fasores das três correntes dadas. Para tal, basta usar as amplitudes e fases iniciais das três funções acima para escrever os respetivos fasores e somá-los (no caso da primeira função é necessário subtrair ao argumento, para substituir o seno por cosseno, pois :
O lado esquerdo da figura seguinte mostra o resultado dessa soma no plano complexo.
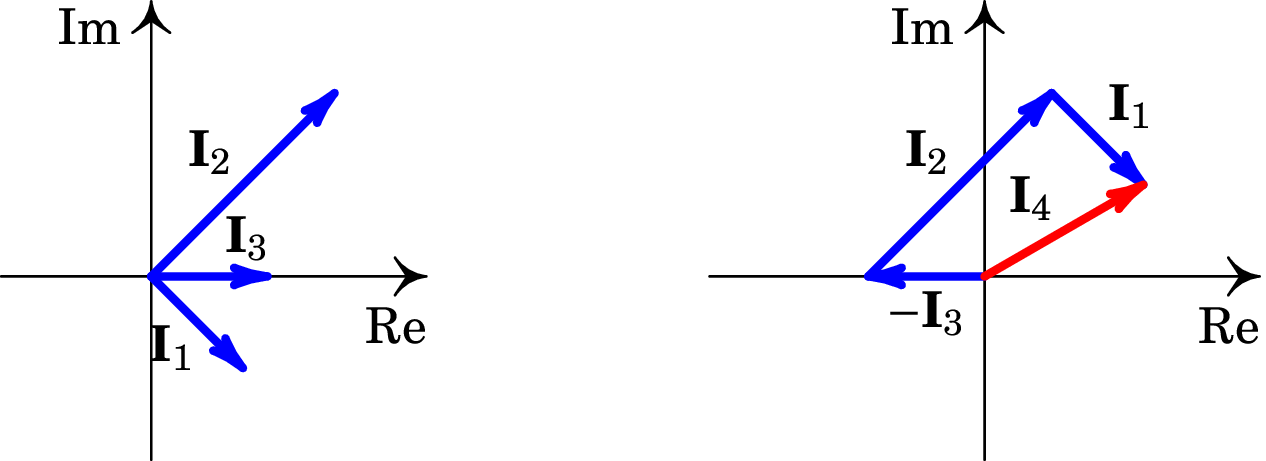
Transformemos agora os fasores da forma polar para a sua forma retangular:
A soma de números complexos é feita no plano complexo somando as partes reais e as partes imaginárias (ver lado direito da figura acima), e o resultado é:
O módulo deste fasor é a hipotenusa do triângulo retângulo com catetos de e 1 unidades (fasor na figura acima), que é,
e a sua fase é o ângulo oposto ao cateto de comprimento 1 nesse triângulo retângulo,
O fasor da corrente pretendida é pois e portanto a corrente é:
10.3 Impedância
O produto de um fasor por um número é outro fasor e a derivada de um fasor em ordem ao tempo é o fasor original multiplicado por um número complexo. Como tal, a lei de Ohm (5.35), a equação (6.28) para os condensadores e a a equação (9.19) para os indutores implicam que nos circuitos de corrente alternada o fasor da tensão em qualquer resistência, condensador ou indutor será igual a um número, que pode ser complexo, vezes o fasor da corrente:
| (10.13) |
em que o número complexo é chamado impedância. Numa combinação de resistências, condensadores e indutores a impedância total será um número complexo com parte real e parte imaginária.
A equação (10.13) pode ser considerada uma generalização da lei de Ohm. Separando a impedância nas suas partes real e imaginária,
| (10.14) |
as funções reais e são designadas de resistência e reatância. A resistência é sempre positiva, independentemente da frequência angular , enquanto que a reatância pode ser positiva para algumas frequências (reatância indutiva) e negativa para outras frequências (reatância capacitiva).
Para um determinado valor de , o módulo e o argumento da impedância podem ser calculados usando a representação gráfica de no plano complexo, obtendo-se o triângulo de impedância apresentado na figura 10.5. Como não pode ter valores negativos, o argumento estará sempre entre e radianos.
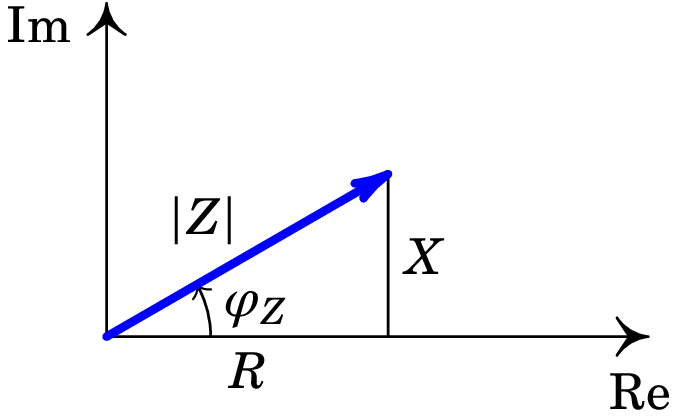
A impedância não é um fasor mas sim um número complexo ordinário, que pode ser multiplicada e somada com outras impedâncias.22Os fasores somam-se como números complexos, mas o produto de dois fasores não pode ser feito multiplicando números complexos porque o produto de duas funções sinusoidais não é outra função sinusoidal. Também pode-se multiplicar ou dividir um fasor por várias impedâncias e o resultado é outro fasor com a mesma frequência.
Em função dos fasores da tensão e da corrente, e , a lei de Ohm (10.13) para fasores é,
| (10.15) |
e a equação complexa (10.13) é equivalente às duas equações reais:
| (10.16) |
10.3.1 Resistências
Numa resistência, a lei de Ohm (5.35) implica que e, como tal, a impedância da resistência é real e igual ao valor da resistência:
| (10.17) |
A impedância tem módulo e argumento nulo. As equações (10.16) indicam que as fases iniciais de e são iguais () e os seus valores máximos verificam a relação,
| (10.18) |
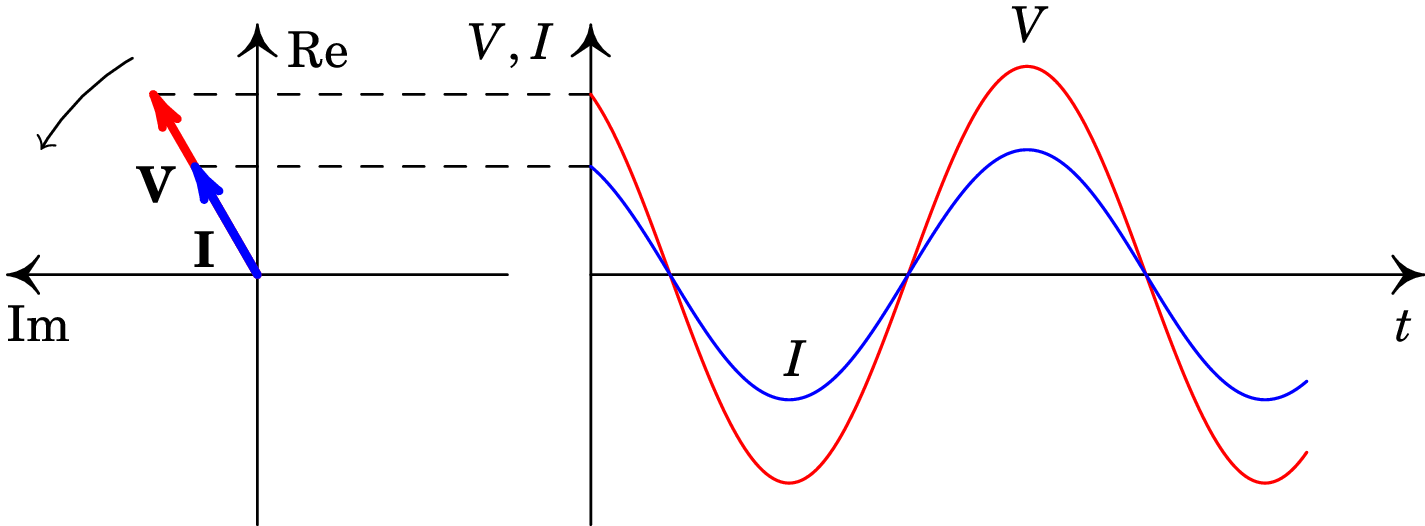
Os vetores no lado esquerdo da figura 10.6 são os fasores no instante = 0, mas como os dois vetores rodam com a mesma velocidade angular, estarão sempre na mesma direção e sentido em qualquer instante. Imaginando esses dois vetores a rodar no sentido anti-horário, com a mesma velocidade angular, as suas projeções no eixo real (tensão e corrente em função do tempo) são as funções apresentadas no lado direito da figura. Diz-se que a tensão e a corrente estão em fase: os dois vetores têm sempre a mesma direção e sentido, de forma que as duas funções atingem os respetivos valores máximo e mínimo em simultâneo.
10.3.2 Condensadores
Num condensador, a expressão (6.28), que relaciona a corrente com a tensão, pode ser escrita da forma,
| (10.19) |
em que pode ser usada qualquer primitiva da função . No apêndice B mostra-se que o fasor da primitiva de um fasor com frequência angular é igual ao fasor original dividido por . Como tal, a relação entre os fasores da tensão e da corrente é,
| (10.20) |
onde a impedância do condensador é:
| (10.21) |
O condensador não tem resistência, apenas reatância, negativa e inversamente proporcional à frequência angular,
| (10.22) |
Aplicando as equações (10.16) obtém-se
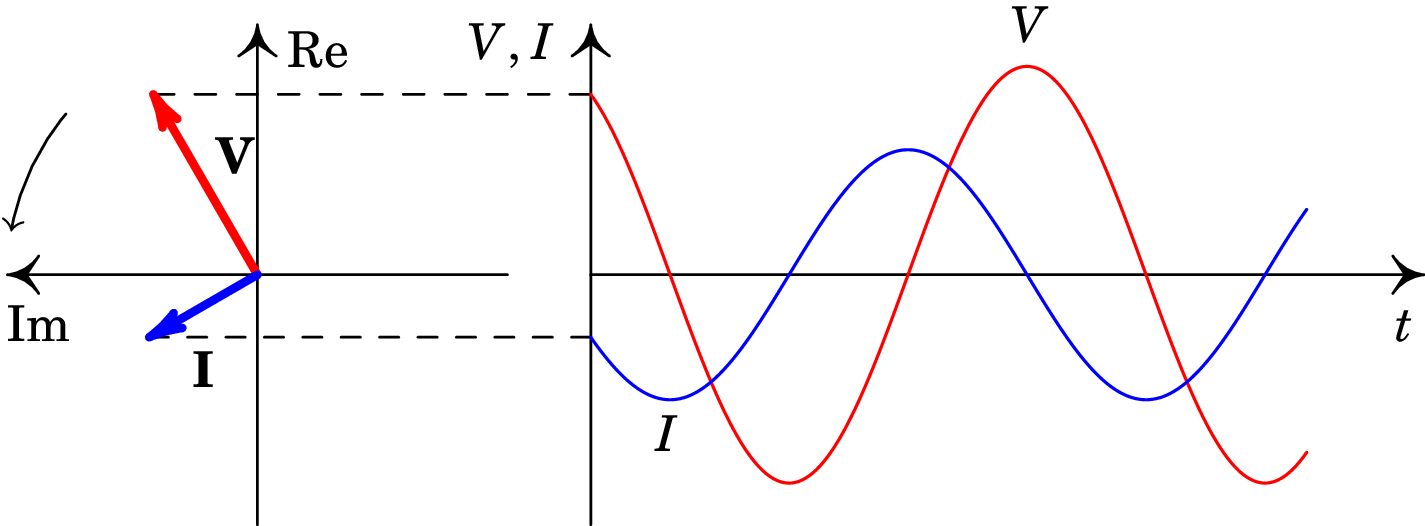
Ou seja, a fase inicial da corrente é maior que a da tensão. Na representação vetorial dos fasores, no lado esquerdo da figura 10.7, a corrente é perpendicular à tensão e está adiantada em relação ao sentido de rotação anti-horário.
Os vetores no lado esquerdo da figura 10.7 estão nas posições em que estão os fasores em ; enquanto esses vetores rodam no sentido anti-horário, com velocidade angular constante, a projeção no eixo real produz as funções representadas no lado direito da figura. Como os dois vetores rodam com a mesma velocidade angular, são perpendiculares em qualquer instante. O desfasamento de entre a corrente e a tensão observa-se nos gráficos do lado direito, pelo facto de ter valor máximo ou mínimo cada vez que é nula. E o facto de ser a corrente a que está adiantada em relação à tensão descobre-se observando dois máximos (ou mínimos), das duas funções e , que estejam próximos entre si: o máximo de ocorre sempre antes do que o máximo de ).
10.3.3 Indutores
Num indutor, a expressão (9.19) que relaciona a corrente com a tensão é,
| (10.23) |
No apêndice B mostra-se que o fasor da derivada de um fasor com frequência angular é igual ao fasor original multiplicado por . Como tal, a relação entre os fasores da tensão e da corrente é,
| (10.24) |
onde a impedância do indutor é:
| (10.25) |
A resistência de um indutor é nula e a sua reatância é positiva e diretamente proporcional à frequência angular:
| (10.26) |
As equações (10.16) implicam que a fase inicial da corrente é menor que a da tensão. Na representação gráfica dos fasores (lado esquerdo da figura 10.8) o fasor da corrente é perpendicular ao da tensão e está atrasado, em relação ao sentido da rotação. Como os dois vetores rodam com a mesma velocidade angular, em qualquer outro instante também são perpendiculares.
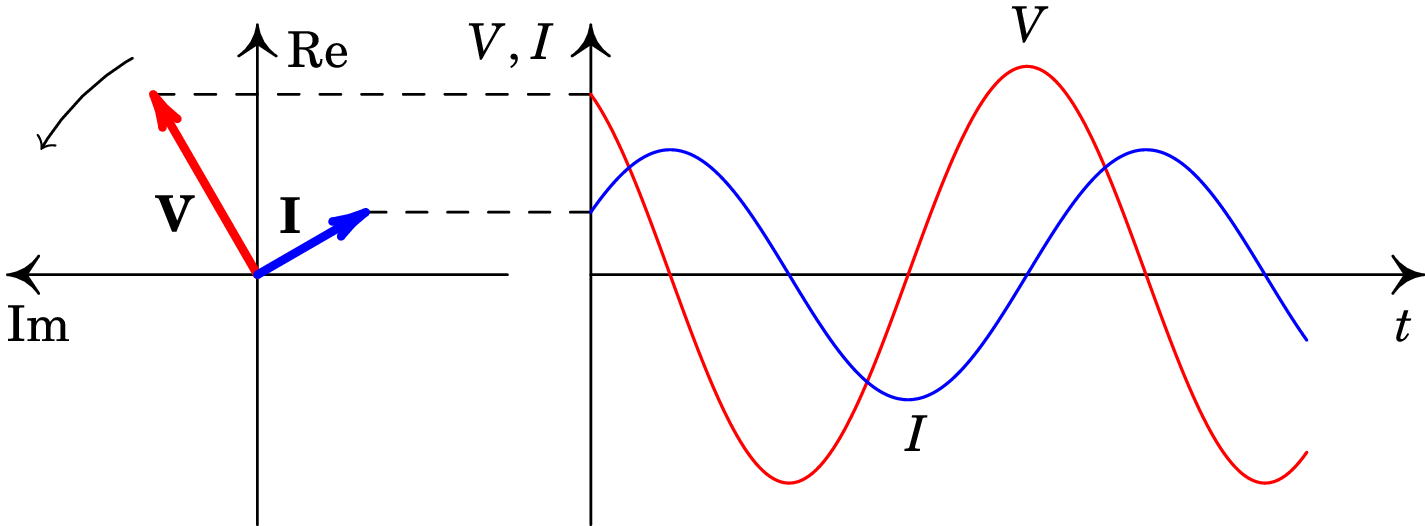
As projeções no eixo real quando os vetores rodam no sentido anti-horário conduzem às duas funções representadas no lado direito da figura. O atraso em do fasor da corrente é visível no gráfico das funções, porque olhando para os valores máximos dessas duas funções, que estão mais próximos entre si, primeiro ocorre o máximo de e a seguir o de . Esse atraso da corrente em em relação à tensão pode também ser observado no gráfico 10.2 da corrente e da tensão no circuito LC da secção 10.1.
10.3.4 Associações de impedâncias
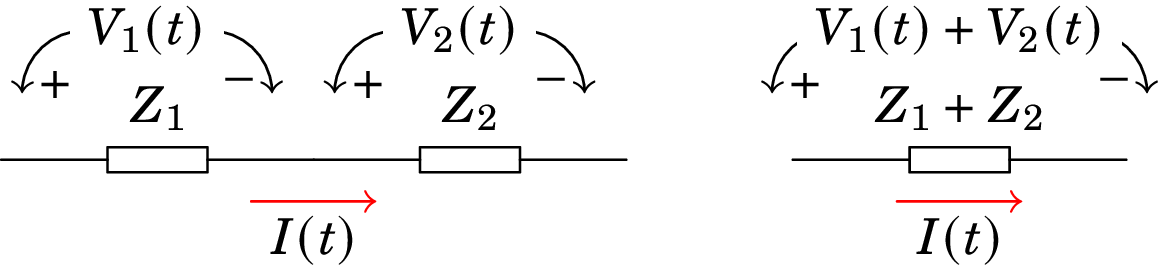
Na secção 5.8 encontrou-se o valor da resistência equivalente para duas resistências ligadas em série ou em paralelo. Para obter as expressões das resistências equivalentes uso-se a lei de Ohm e o facto de que nos dispositivos em série a corrente é a mesma em todos e a tensão total é igual à soma das tensões, enquanto que nos dispositivos em paralelo a tensão é igual em todos e a corrente total é soma das correntes nos dispositivos. Como vimos na equação (10.13), a lei de Ohm aplica-se também aos fasores no caso da corrente alternada. Como tal, a impedância equivalente dos dispositivos ligados em série ou em paralelo obedece as mesmas regras do que as resistências em série ou em paralelo.
No caso de dois dispositivos ligados em série (figura 10.9), a impedância equivalente é igual à soma das impedâncias dos dois dispositivos:
| (10.27) |
Já no caso de dois dispositivos ligados em paralelo (figura 10.10), a impedância equivalente é:
| (10.28) |
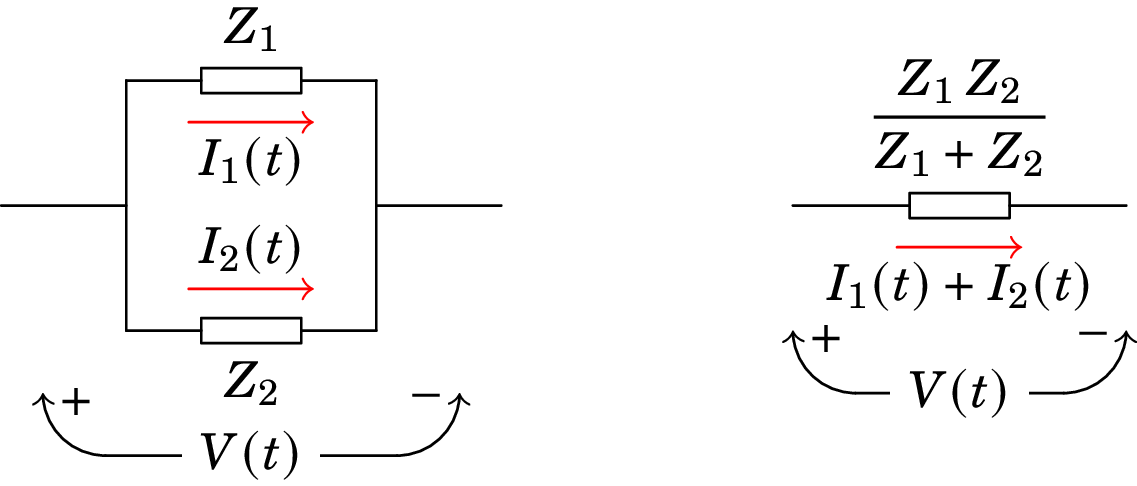
Como as leis de divisão de voltagem e divisão de corrente nas resistências foram obtidas a partir da lei de Ohm, as mesmas leis aplicam-se no caso das impedâncias.
10.3.5 Unidades de impedância, tempo e frequência
A lei de Ohm aplicada a fasores, equação (10.13), implica que as unidades da impedância, qualquer que for o dispositivo, são as mesmas unidades da resistência elétrica. Como a impedância de um condensador é e tem unidades do inverso do tempo, então as unidades da capacidade são unidades de tempo sobre resistência.
De forma semelhante, conclui-se que as unidades de indutância são unidades de resistência vezes tempo. As constantes e que aparecem nas expressões da tensão e da corrente dos circuitos RC e RL (secções 6.6.1 e 9.4.1), têm unidades de tempo. O produto tem unidades de tempo ao quadrado e a constante que apareceu no circuito LC da secção 10.1 tem unidades de frequência. A constante tem unidades de resistência.
Estas relações ajudam na escolha das unidades que simplificam os cálculos num circuito dado. Por exemplo, se as resistências no circuito fossem da ordem dos k e as capacidades da ordem dos nF, a unidade de tempo mais conveniente seria o µs (produto entre k e nF), a unidade de indutância mais conveniente seria então o mH (produto entre µs e k) e a unidade de frequência mas conveniente seria MHz (inverso de µs). Convertendo os valores das resistências para k, as capacidades para nF, as indutâncias para mH, os tempos para µs e frequências para MHz, teremos um sistema de unidades consistente.
Exemplo 10.2
Calcule a tensão e corrente instantâneas em todos os elementos do circuito representado no diagrama.
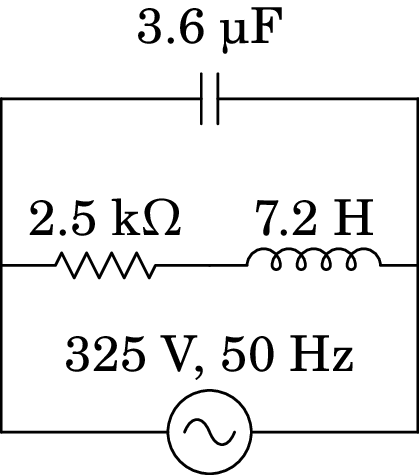
Resolução. Usando unidades de k para as impedâncias e µF para as capacidades, teremos então de usar ms como unidade de tempo e H como unidade de indutância. Usando V para as tensões, as correntes estarão em mA. A frequência angular da fonte é: Hz, mas como deve ser convertida para kHz, tem o valor .
A impedância da resistência é 2.5, a do condensador e a do indutor é . Como a resistência está em série com o indutor, podem ser substituídos por um único elemento com impedância igual à soma das impedâncias:
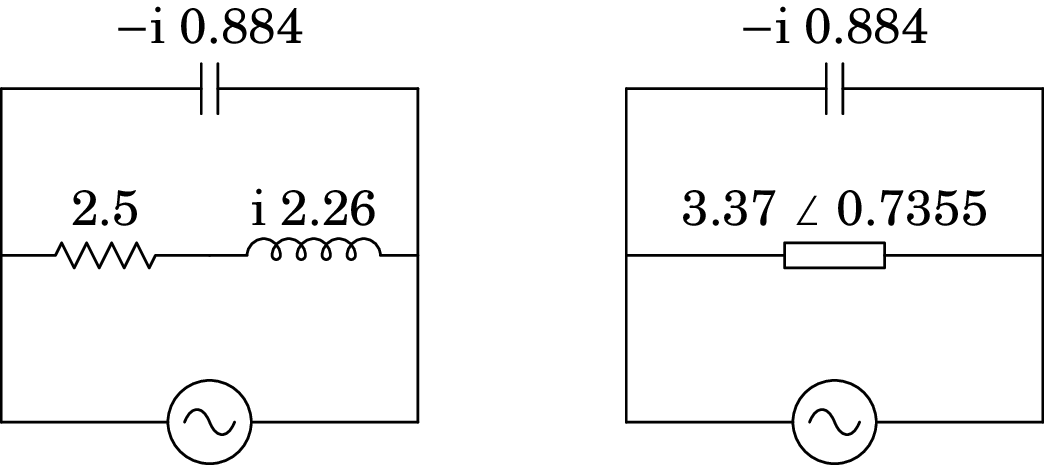
Como os dois elementos no circuito simplificado estão em paralelo, o fasor da tensão é o mesmo para os dois e igual ao fasor da fonte: . Dividindo esse fasor pelas impedâncias dos dois elementos, calculam-se os fasores das correntes (lado esquerdo da figura seguinte). Em seguida, multiplicando o fasor da segunda corrente pelas impedâncias da resistência e do indutor, calculam-se os fasores das tensões (lado direito da figura seguinte):
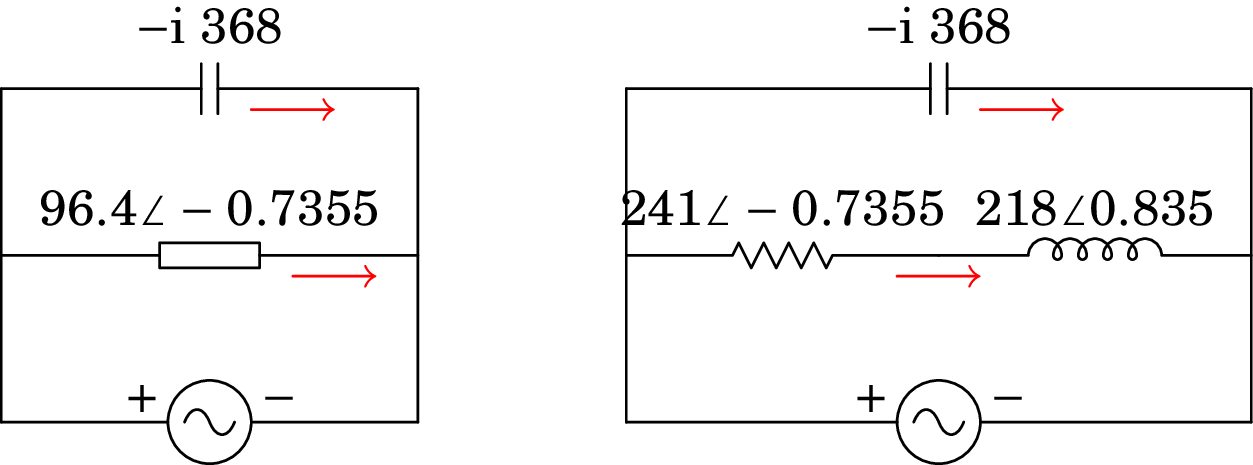
A partir dos fasores podem-se exprimir as tensões e correntes instantâneas:
10.4 Potência nos circuitos de corrente alternada
Em qualquer ponto de um circuito de corrente alternada, a corrente é uma função sinusoidal; em cada período de oscilação, a mudança de sinal da função sinusoidal indica que o sentido da corrente muda. O integral da função em cada período é nulo, o quer dizer que a carga total transferida é nula. Durante metade do período há transporte de carga num sentido e no meio período seguinte a mesma carga é transportada no sentido oposto.
Não há transferência efetiva de carga nos circuitos de corrente alternada. As cargas de condução simplesmente oscilam à volta de uma posição de equilíbrio. Apesar de não haver transferência efetiva de cargas, há dissipação efetiva de energia elétrica, pois a oscilação das cargas é contrariada pela resistência dos condutores e há efeito Joule, independentemente do sentido da corrente.
Em qualquer dispositivo passivo num circuito com fonte de tensão alternada, a tensão e a corrente são funções sinusoidais com a mesma frequência da fonte, após uma possível resposta transitória inicial:
| (10.29) |
A potência instantânea, , é a potência no dispositivo em qualquer instante
| (10.30) |
Usando uma relação trigonométrica para o produto de dois cossenos e o facto de ser (equação (10.16)), conclui-se que a expressão anterior é equivalente a:
| (10.31) |
Note-se que o primeiro cosseno dentro dos parêntesis retos na equação (10.31) é uma função sinusoidal, com frequência igual ao dobro da frequência da fonte, enquanto o segundo cosseno é uma função constante. Assim, o produto de duas funções sinusoidais (neste caso e ) com a mesma frequência não conduz a outra função sinusoidal com a mesma frequência, mas a uma função sinusoidal com o dobro da frequência, mais uma constante.
A potência instantânea (10.31) pode ser positiva ou negativa em alguns intervalos e nula em alguns instantes, dependendo do valor da constante , chamada fator de potência. Como está entre e , o fator de potência situa-se entre 0 e 1.
Se a reatância for nula (dispositivo resistivo) o argumento da impedância () é nulo, o fator de potência é igual a 1 e a potência instantânea é sempre positiva, indicando que o dispositivo está sempre a dissipar energia.
Já se a resistência for nula (dispositivo reativo), o argumento da impedância é , o fator de potência é nulo, e os intervalos em que a potência instantânea é positiva possuem a mesma duração que os intervalos em que é negativa pelo que a potência média é nula. Como exemplo, tomemos o ciruito LC da secção 10.1. A energia inicialmente armazenada no condensador sob a forma de energia elétrica é transformada em energia armazenada no indutor sob a forma de energia magnética, sendo depois sucessivamente trocada entre o indutor e o condensador. Neste caso, não há nem dissipação de energia nem fornecimento de energia, conservando-se a energia total. 33 Esta situação é análoga ao sistema massa-mola sem atrito, onde a energia cinética da massa e a energia potencial elástica da mola se transformam uma na outra sucessivamente, ou a um pêndulo simples gravítico sem atrito, onde a energia cinética e a energia potencial gravítica se transformam continuamente uma na outra, mas a energia total conserva-se.
No caso geral, em que o fator de potência é maior que 0 e menor que 1, os intervalos em que há dissipação de energia são mais compridos do que os intervalos em que há fornecimento de energia e, em média, o circuito dissipa energia.
O valor médio da potência, , calcula-se integrando a função (10.31) durante um período e dividindo pelo valor do período. O integral do primeiro termo é nulo, durante um período, enquanto que o valor médio do termo constante é igual a si próprio. Consequentemente, a potência média é:
| (10.32) |
e tem valor positivo ou nulo, indicando que, em média o dispositivo passivo não pode fornecer energia. É também habitual definir a tensão eficaz e a corrente eficaz:
| (10.33) |
e como tal, a potência média é igual ao produto da tensão e corrente eficazes e o fator de potência:
| (10.34) |
A tensão máxima de 325 V usada na União Europeia corresponde a uma tensão eficaz de 230 V. No continente americano usa-se tensão máxima de 170 V, a 60 Hz, que corresponde a uma tensão eficaz de 120 V.
10.5 Filtros de frequência
Um filtro de frequência é um circuito passivo usado para modificar uma tensão alternada. A tensão alternada que vai ser modificada é considerada a tensão de entrada, , e a tensão modificada é considerada a tensão de saída, , do filtro. Podemos analisar o filtro como qualquer outro circuito de corrente alternada em que há uma fonte de tensão e a tensão em alguma parte do circuito é designada por .
Se o circuito é composto por resistências, indutores e condensadores, o fasor da tensão de saída, , será sempre proporcional ao fasor da tensão de entrada, , ou seja,
| (10.35) |
onde é uma função complexa denominada função de resposta em frequência.
Se a tensão de entrada for a tensão alternada,
| (10.36) |
o fasor de entrada será e o fasor de saída será,
| (10.37) |
onde e são o módulo e o argumento da função complexa , ambos dependentes da frequência angular .
A tensão de saída é então a função,
| (10.38) |
Assim, um filtro é caraterizado por uma função complexa e o efeito do filtro é multiplicar o valor máximo da tensão de entrada pelo módulo de e desfasá-la num ângulo igual ao argumento de .
Exemplo 10.3
Determine a função de resposta em frequência do filtro passa-alto representado na figura.
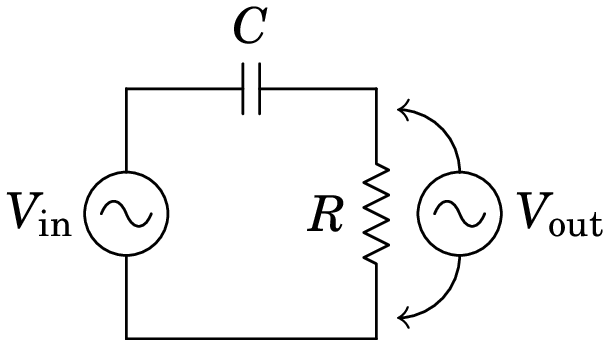
Resolução. A impedância da resistência é e a impedância do condensador é . Como a resistência e o condensador estão em série, a lei de divisão da voltagem conduz ao fasor da tensão de saída:
A função de resposta em frequência é então,
com módulo e argumento:
| (10.39) |
Onde , com unidades de frequência, é designada por frequência angular de corte do filtro.
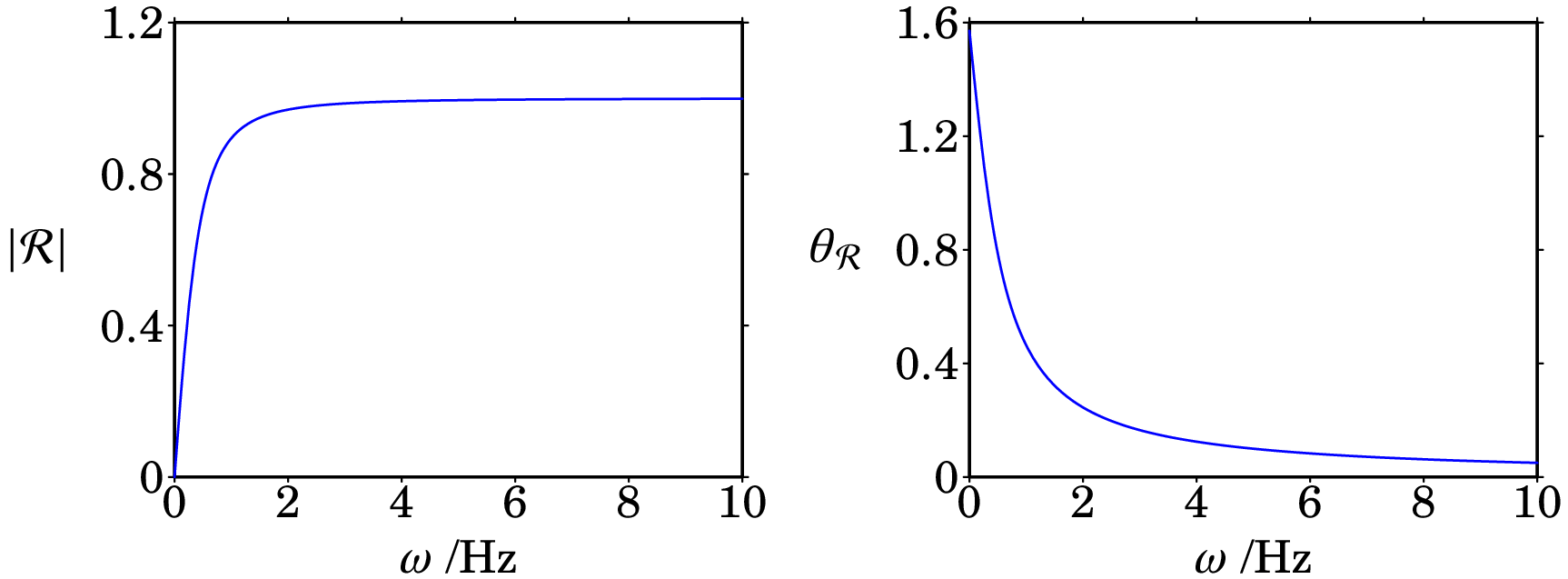
A figura 10.11 mostra o módulo e o argumento da função de resposta em frequência de um filtro passa-alto com frequência angular de corte igual a Hz 44A frequência angular de corte, dependendo apenas de e , que são constantes, é uma característica intrínseca do filtro.. No limte em que , usando as equações do exemplo 10.3, temos que (, ), pelo que a tensão de saída é nula. Este limite de frequência nula corresponde a uma tensão de entrada contínua, a reactância do condensador é infinita e a função de resposta é nula.
Este resultado está de acordo com o anteriormente obtido na secção 6.8 de que um condensador, no seu estado estacionário, não deixa passar corrente elétrica contínua, sendo equivalente a um circuito aberto. Observe-se que em , tem módulo e argumento . Note-se ainda que no limite em que temos que e , pelo que a tensão de saída é igual à de entrada. Neste limite de frequência infinita, a impedância do condensador é nula, comportando-se o condensador portanto como um curto-circuito.
Este filtro é denominado por passa-alto, porque as frequências menores do que a frequência de corte são atenuadas enquanto que se a frequência for muito maior do que a de corte, o sinal de saída é aproximadamente igual ao sinal de entrada. Por outras palavras, um filtro passa-alto, essencialmente deixa passar apenas as frequências mais altas (comparadas com a de corte).
Vários filtros podem ser combinados de forma sequencial e a função de resposta é o produto das funções de todos os filtros na sequência. Por exemplo, o filtro passa-banda da figura 10.12 é a combinação de um filtro passa-alto, com frequência angular de corte e um filtro passa-baixo, com frequência angular de corte .
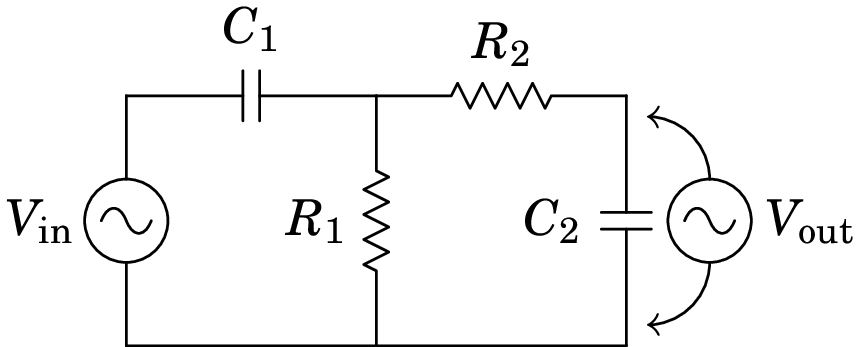
A função de resposta em frequência deste filtro (problema 10.10.12) é a seguinte:
| (10.40) |
onde , chamado ganho do filtro, é uma constante sem unidades. O módulo dessa função, , é nulo em e no limite , e tem valor máximo quando a frequência angular for igual à média geométrica das duas frequências de corte: .
Um filtro ideal teria uma função de resposta nula para as frequências que se pretende eliminar, e igual a 1 nas outras frequências. Com circuitos mais complicados conseguem-se obter filtros com comportamento mais próximo do ideal. Outro fator a ter em conta é a resposta transitória, que tem sido ignorada por ser nula após algum tempo, mas num filtro de boa qualidade é necessário garantir que a resposta transitória desaparece rapidamente.
10.6 Ressonância
Quando um circuito com condensadores e indutores é ligado a diferentes fontes com a mesma tensão máxima , mas com diferentes frequências, a potência absorvida pelo circuito varia em função da frequência. Normalmente, existe uma frequência de ressonância tal que a potência dissipada pelo circuito é máxima. Se a frequência da fonte é igual à frequência de ressonância do circuito, diz-se que o circuito está em ressonância com a fonte.
No caso particular do circuito RLC, com uma resistência, um indutor e um condensador em série, a reatância equivalente é função contínua da frequência . Quando se aproxima de infinito ou de zero, o valor absoluto da reatância aproxima-se de infinito. Como tal, a corrente nos 3 dispositivos é nula. A frequência de ressonância é a frequência que faz com que a reatância seja nula e o módulo da impedância seja mínimo: . Isso implica que o argumento da impedância seja nulo, , e o fator de potência igual a 1, . A corrente máxima e a potência média em função de serão ambas máximas e a tensão e a corrente estarão em fase.
A frequência (ou frequências) de ressonância é um valor caraterístico de cada circuito. Nos circuitos em que os indutores e condensadores não estão em série, a frequência de ressonância pode surgir quando a reatância não é nula, com fator de potência diferente de 1, i.e, corrente desfasada da voltagem.
Exemplo 10.4
Determine a frequência de ressonância do circuito e a potência média no circuito representado no diagrama seguinte.
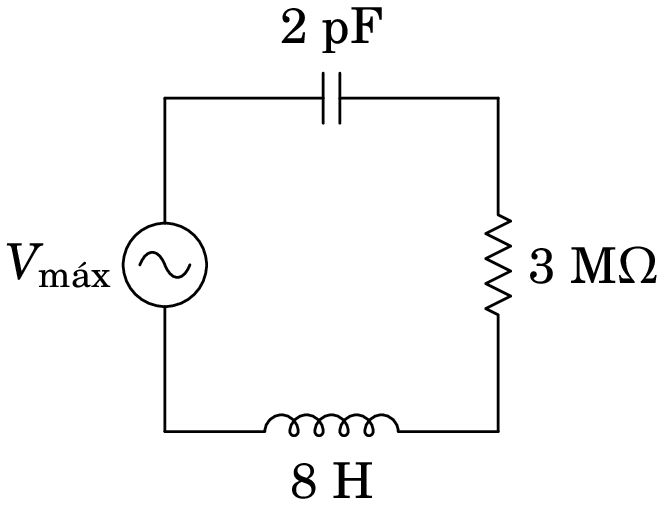
Resolução. Com a resistência em M e a capacidade em pF, a unidade de tempo será µs e, portanto, a frequência será dada em MHz e a indutância deverá estar em H.
A impedância total do circuito é a soma das 3 impedâncias:
Observe-se que a parte real da impedância não depende da frequência, angular porque o condensador e o indutor estão em série com a resistência e, como tal, o valor mínimo do módulo da impedância obtém-se quando a parte imaginária seja igual a zero:
No sistema de unidades usado, a frequência de ressonância é MHz, igual a kHz.
Se a fonte tivesse essa frequência, a impedância equivalente seria real, M, e a corrente máxima teria o valor (µA, se estiver em volts). A potência média máxima é (µW, se estiver em volts).
No circuito do exemplo anterior, a fonte faz oscilar a carga no condensador. Se a fonte fosse desligada, a carga oscilaria com a frequência angular própria de um circuito (equação (10.4)). Se a frequência angular da fonte for diferente de , as duas oscilações interferem produzindo uma oscilação com amplitude menor, mas se as duas frequências angulares forem iguais, as duas oscilações reforçam-se mutuamente produzindo oscilação com maior amplitude.
A situação é semelhante a uma massa pendurada de uma mola elástica, na qual atua uma força externa que tenta manter a massa oscilando para cima e para baixo. Se a força externa não oscila com a mesma frequência própria de oscilação do sistema mola-massa, há momentos em que a força externa está a tentar fazer subir a massa, enquanto a mola elástica faz força no sentido oposto; mas quando a força externa tiver a mesma frequência do sistema mola-massa, as duas forças atuam sempre no mesmo sentido e a amplitude de oscilação é máxima.
Se a resistência fosse nula, quando a frequência da fonte fosse a frequência de ressonância, seria nula e aparentemente seria infinita. No entanto, a corrente não aumentaria instantaneamente até esse valor, mas sim gradualmente, com as oscilações da carga no condensador. Quando essa carga máxima fosse muito elevada, haveria rutura do dielétrico no condensador ou a corrente elevada queimaria o indutor.
Problemas
-
10.1.
A resistência de uma bobina é 150 e a sua indutância é 1.4 H. A bobina é ligada à rede elétrica com tensão máxima 325 V e frequência de 50 Hz. Encontre a expressão para a corrente na bobina em função do tempo .
-
10.2.
Nos dois circuitos representados na figura, calcule a corrente e a tensão em todos os elementos do circuito.
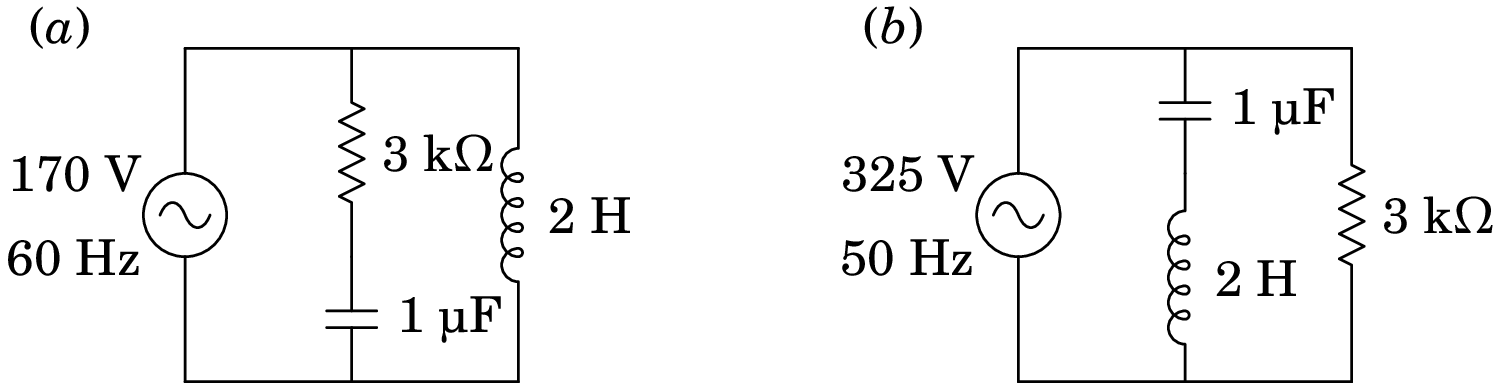
-
10.3.
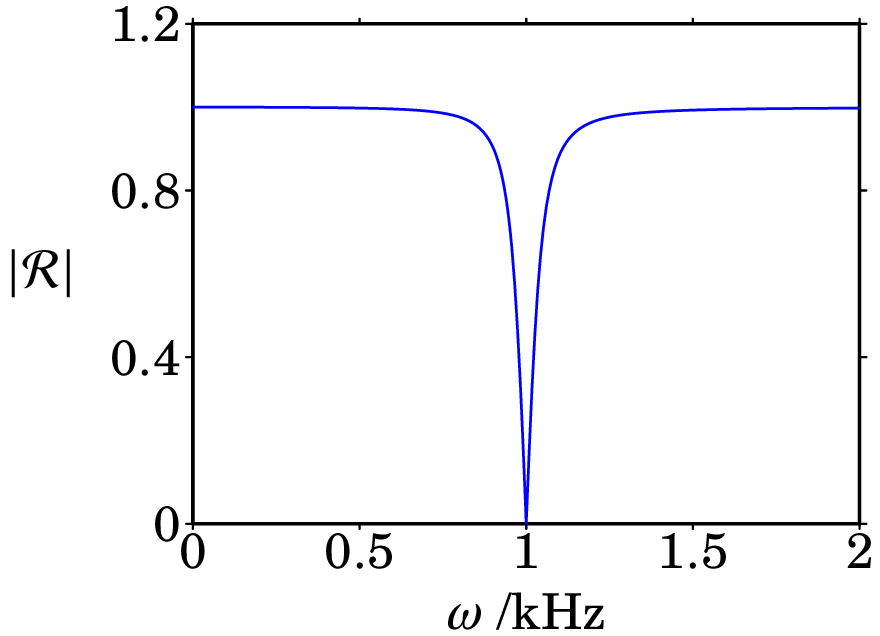
A figura mostra um filtro rejeita-banda que atenua as frequências angulares próximas de 1 kHz.
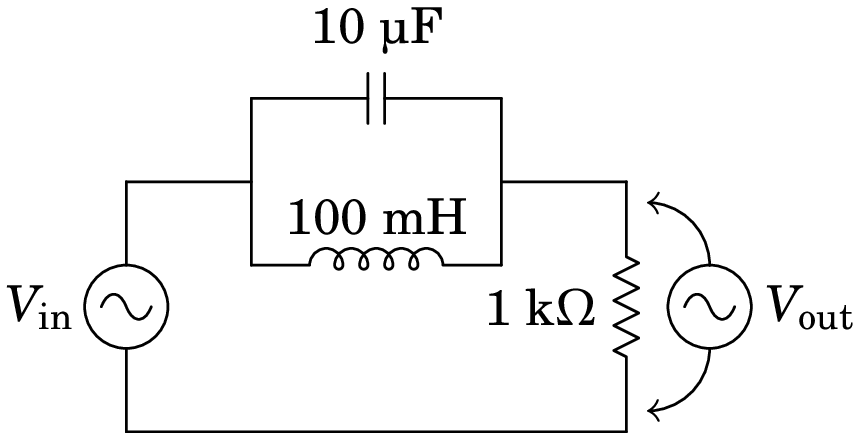
(a) Determine a função de resposta em frequência, , do circuito.
(b) Mostre que para kHz, é igual a zero.
(c) Calcule o módulo de e trace o seu gráfico para entre 0 e 2 kHz. -
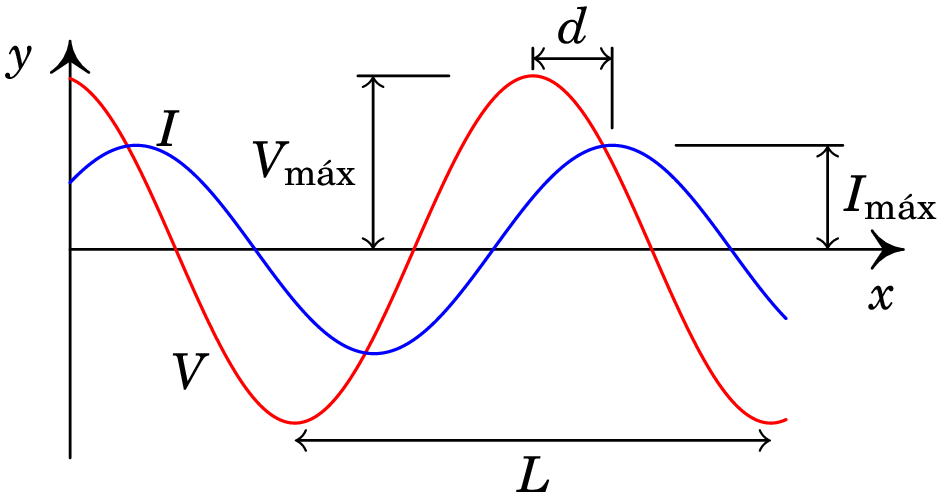
10.4.
A figura mostra o ecrã de um osciloscópio onde aparecem a tensão e a corrente num elemento de um circuito. As distâncias e foram medidas diretamente no ecrã, obtendo-se os valores cm e cm. O osciloscópio também permite determinar que a tensão máxima é V e a corrente máxima é mA. Com esses dados, calcule a parte real e a parte imaginária da impedância do elemento do circuito.
-
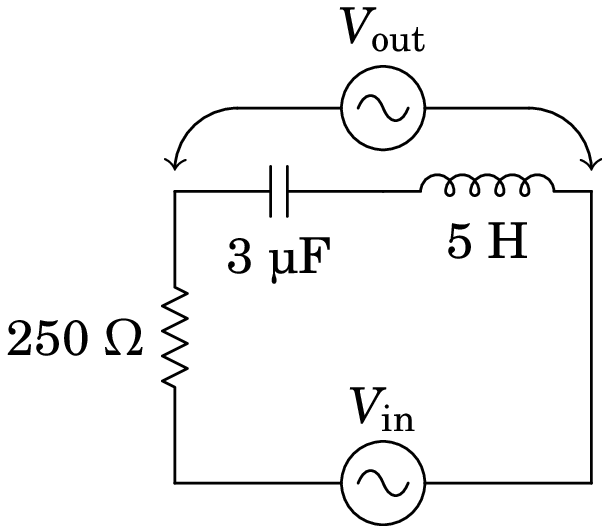
10.5.
No filtro de frequências representado no diagrama, o sinal de entrada é a tensão de uma fonte de tensão alternada, com frequência angular , e o sinal de saída é a tensão medida no indutor e no condensador, como indica a figura. Encontre a expressão da função de resposta em frequência.
-
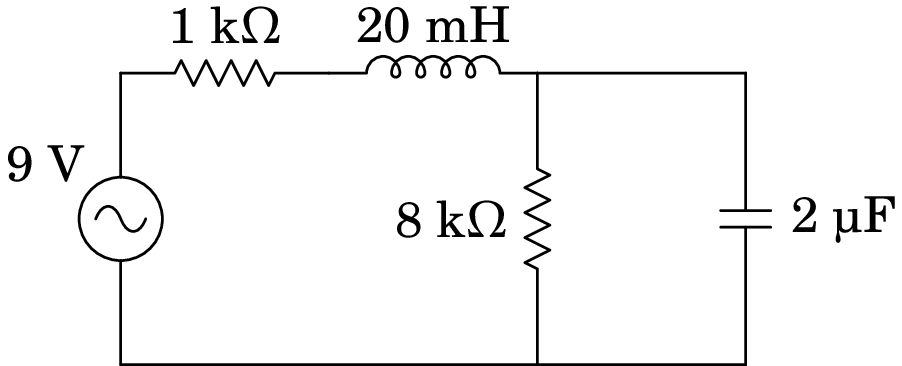
10.6.
No circuito representado no diagrama, determine a potência média fornecida pela fonte, sabendo que esta tem frequência de 30 Hz e voltagem máxima de 9 V.
-
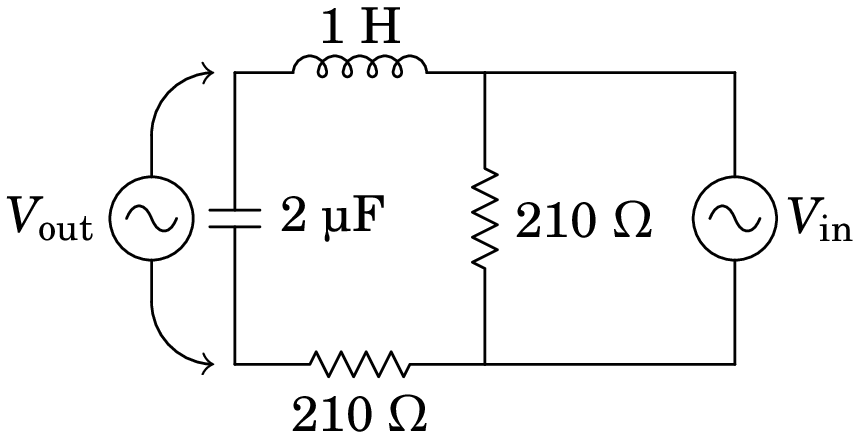
10.7.
No filtro de frequências representado no diagrama, o sinal de entrada é a tensão de uma fonte de tensão alternada, com frequência angular , e o sinal de saída é a tensão medida no condensador, como indica a figura. Encontre a expressão da função de resposta em frequência, em função de .
-
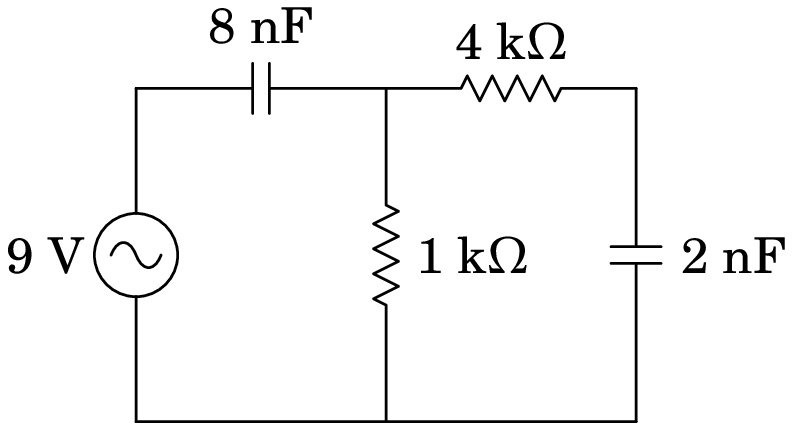
10.8.
A fonte no circuito representado no diagrama tem voltagem máxima 9 V e frequência angular kHz. Determine a voltagem máxima no condensador de 2 nF.
-
10.9.
Uma bobina, com indutância de 36 mH e resistência de 40 , liga-se em paralelo com um condensador de 32 nF e com uma fonte de tensão alternada (em volts se o tempo estiver em segundos). Calcule:
(a) A corrente máxima na bobina.
(b) A corrente eficaz no condensador.
(c) As potências médias dissipadas na bobina e no condensador. - 10.10.
-
10.11.
Num segmento de um circuito de corrente alternada a tensão em função do tempo é dada pela expressão (em volt, com em milissegundos) e a corrente é (µA, com em ms).
(a) Calcule a resistência e reatância desse segmento.
(b) O segmento do circuito pode ser substituído por apenas dois dispositivos. Diga quais são esses dispositivos e com que valores. -
10.12.
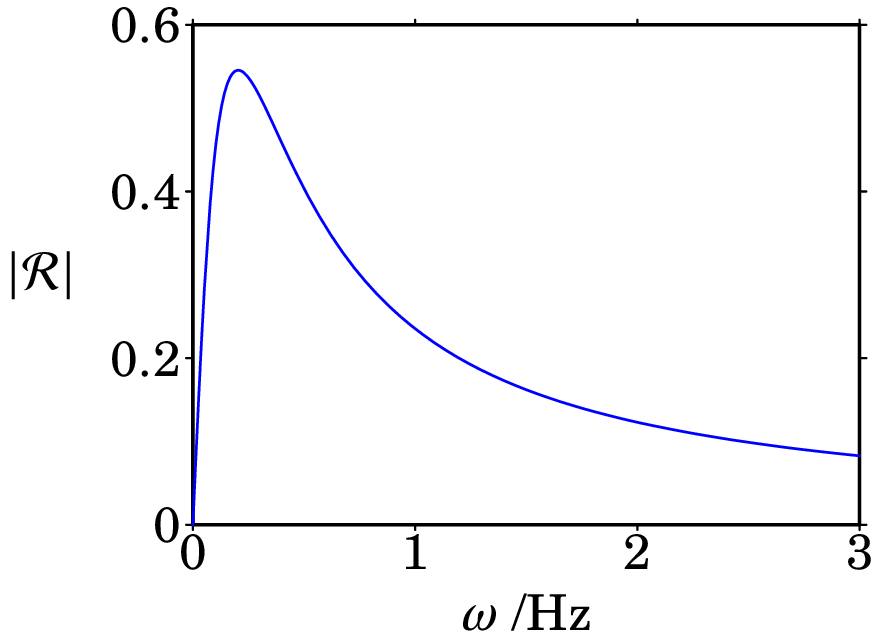
O seguinte diagrama mostra um filtro passa-banda:

(a) Demonstre que a função de resposta em frequência é a expressão na equação (10.40), onde , e .
(b) Determine o valor máximo de e a frequência angular em que essa função é máxima.
(c) Trace o gráfico de , com , entre 0 e 3 kHz, no caso particular µF, µF, k e k -
10.13.
Um condensador de µF, um indutor de H e uma resistência de k ligam-se em série a uma fonte de tensão alternada, com voltagem máxima de V e frequência de Hz. Encontre a expressão da voltagem no indutor, em função do tempo.
-
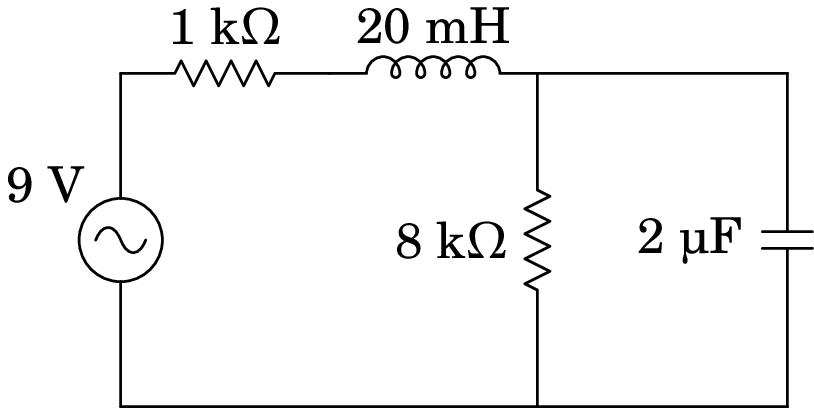
10.14.
No circuito representado no diagrama, determine a potência média fornecida pela fonte, sabendo que esta tem frequência de 30 Hz e voltagem máxima de 9 V.
-
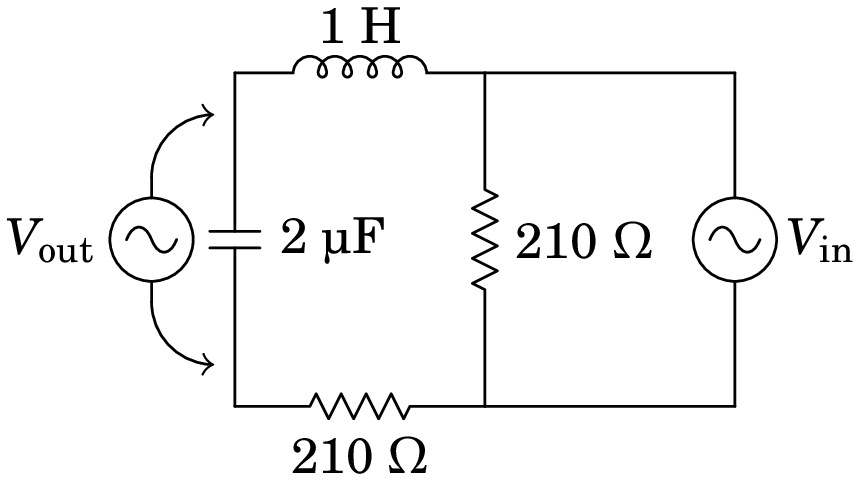
10.15.
No filtro de frequências representado no diagrama, o sinal de entrada é a tensão de uma fonte de tensão alternada, com frequência angular , e o sinal de saída é a tensão medida no condensador, como indica a figura. Encontre a expressão da função de resposta em frequência, em função de .
-
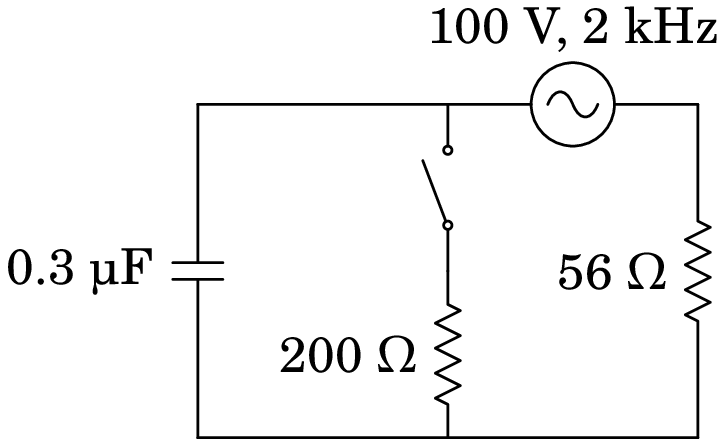
10.16.
A fonte no circuito representado no diagrama tem tensão eficaz de 100 V e frequência de 2 kHz. Calcule a corrente eficaz na resistência de 56 , quando o interruptor estiver aberto e quando estiver fechado.
Respostas
-
10.1.
A.
-
10.2.
(a) Com tensões em V, correntes em mA e tempo em ms,
No condensador:
Na resistência:
No indutor:
(b) Com tensões em V, correntes em mA e tempo em ms,
No condensador:
Na resistência:
No indutor:
-
10.3.
(a) (c)
-
10.4.
-
10.5.
-
10.6.
8.15 mW.
-
10.7.
( em kHz).
-
10.8.
4 V.
-
10.9.
(a) 7.94 A. (b) 3.68 mA (c) 1.261 kW na bobina e 0 no condensador.
-
10.10.
kHz, mA, µC.
-
10.11.
(a) resistência e reatância . (b) Uma resistência de 2.63 M e um condensador de 2.21 nF, ligados em série.
-
10.12.
(b) , .
(c) O gráfico é o seguinte:
-
10.13.
(unidades SI).
-
10.14.
8.15 mW.
-
10.15.
-
10.16.
0.483 mA.