7. Força magnética

William Gilbert (1544–1603)
Gilbert trabalhou como médico ao serviço da corte inglesa. Em 1600 publicou o primeiro tratado rigoroso sobre o magnetismo, De Magnete (título em latim que significa acerca do magnetismo). Gilbert reconhece a importância da experimentação direta e no seu livro descreve as muitas experiências que realizou. Entre os principais contributos conta-se a explicação do funcionamento da bússola e a conclusão de que a própria Terra é um íman com dois polos magnéticos. Gilbert descobre também que quando um íman é dividido em duas partes cada um dos fragmentos é outro íman com dois polos; estudou também a força elétrica e mostrou as diferenças com a força magnética entre ímanes.
A força magnética é também um tipo de força que atua a distância, sem necessidade de um meio nem de contacto, tal como a força gravítica e a força elétrica. Pode ser atrativa ou repulsiva, o que fez com que fosse confundida com a força elétrica desde a época dos gregos em que já eram conhecidas essas duas forças, até 1600, quando William Gilbert a identificou como uma força diferente da elétrica. Na Grécia antiga, as rochas extraídas das minas da região da Magnésia eram ímanes naturais que deram origem ao termo magnetismo.
Um íman tem sempre um polo norte e um polo sul. Aproximando os polos opostos de dois ímanes, surge uma força atrativa entre eles; entre polos semelhantes a força é repulsiva. A própria Terra é também um íman natural e, por isso, a bússola aponta na direção do polo norte geográfico. A bússola, que é também um pequeno íman tem dois polos e serve para definir qual dos polos é o polo norte e qual o sul num íman. O polo norte da bússola é o que aponta na direção do norte geográfico; se colocarmos a bússola próxima de um dos polos de outro íman, rodará e o polo desse íman será o oposto do polo da bússola que fica mais próximo dele.
Partindo um íman em vários pedaços menores, em cada pedaço aparecem sempre um polo norte e um polo sul. É impossível obter um íman com unicamente um polo norte ou sul. Isto significa que não existem monopolos magnéticos. Esta é a maior diferença em relação à força elétrica, onde podem existir cargas positivas e negativas (os "monopolos" elétricos) isoladamente.
7.1 Campo magnético
Tal como no caso da força elétrica, a força magnética sobre um objeto pode ser descrita como a sua interação com o campo magnético existente na posição onde se encontra o objeto. Uma bússola roda e aponta na direção norte, devido à sua interação com o campo magnético terrestre. Em cada ponto define-se a direção das linhas de campo magnético na direção em que aponta a bússola e seguindo essas direções obtêm-se linhas contínuas que são as linhas de campo magnético.
Para obter as linhas de campo magnético produzidas por um íman retangular como o da figura 7.1, coloca-se uma pequena bússola em diferentes pontos próximos do íman. Define-se o sentido das linhas de campo como o sentido em que aponta o polo norte da bússola.
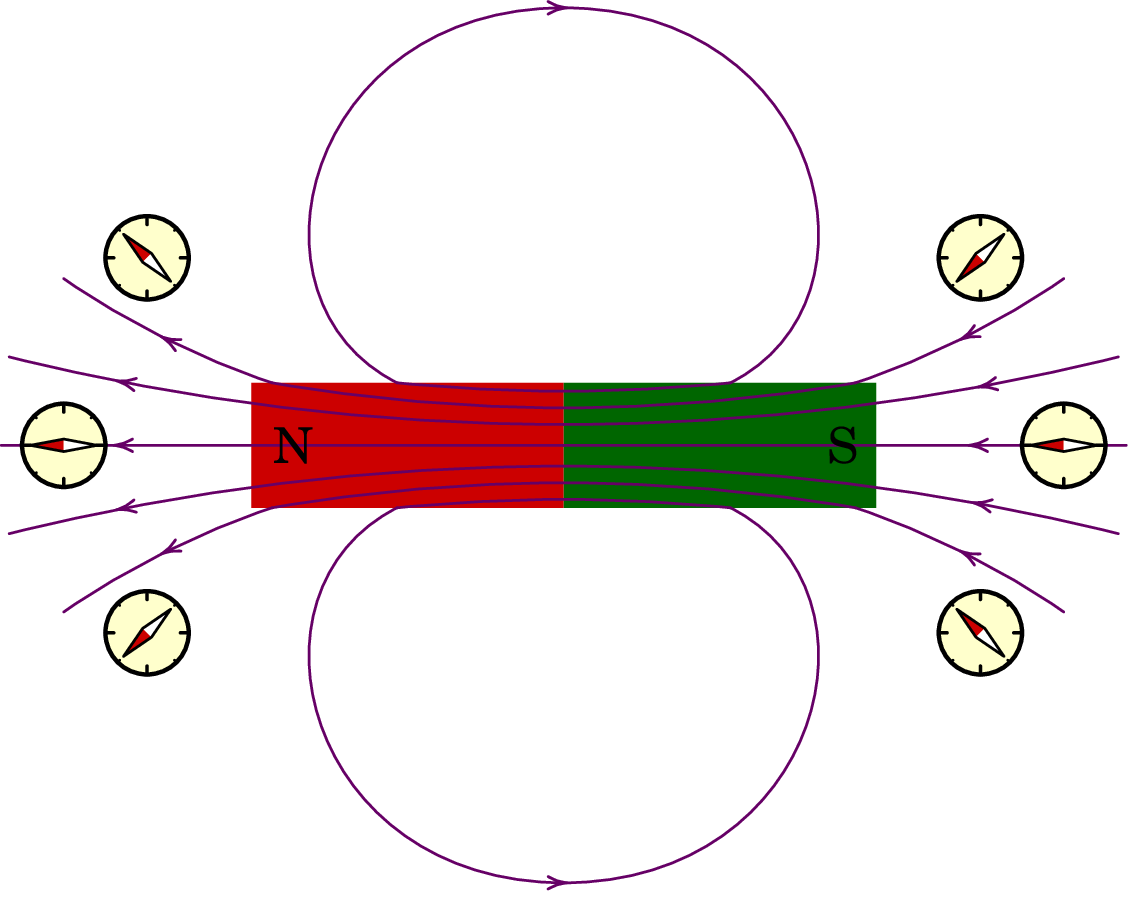
Em cada ponto define-se o vetor de campo magnético, , tangente às linhas de campo e na direção em que estas apontam. As linhas de campo saem do polo norte e entram no polo sul. Observe-se que as linhas de campo continuam dentro do íman e que se fecham sobre si próprias. Um ponto do espaço onde houvesse linhas de campo magnético a convergir ou divergir em todas as direções implicaria um monopolo magnético, os quais nunca foram observados experimentalmente.
O facto de as linhas de campo serem fechadas também implica que o campo magnético não é conservativo, já que o integral de linha ao longo de uma das linhas de campo fechada é diferente de zero, porque a componente do campo na sua própria direção é igual ao seu módulo, positivo; como vimos, num campo conservativo, o seu integral de linha numa curva fechada tem de ser nulo.
Se a bússola usada na figura 7.1 é suficientemente pequena, ao longo do seu comprimento as linhas de campo do íman são aproximadamente constantes, i.e., o campo magnético é aproximadamente uniforme nessa região. Nesse caso a bússola roda, mas não é atraída para o íman. A situação é análoga à de um dipolo elétrico dentro de um campo elétrico uniforme, em que a força elétrica total sobre o dipolo é nula, mas há um binário não nulo que faz rodar o dipolo (ver problema 1.14 do capítulo 1.)
Para definir a intensidade do campo magnético em cada ponto é necessário algum objeto pequeno no qual atue uma força magnética suficientemente elevada para poder ser medida. Um pequeno íman não serve, mas uma partícula com carga elétrica, em movimento, pode sofrer uma força magnética mesurável numa região onde exista campo magnético.
Experimentalmente observam-se as seguintes caraterísticas da força magnética, , sobre uma partícula de carga com velocidade , num ponto onde existe um campo magnético :
-
1.
Mantendo a direção da velocidade constante e mudando o seu módulo, , observa-se que a força é diretamente proporcional a .
-
2.
Mantendo o módulo da velocidade constante e mudando a sua direção, a força é máxima quando a velocidade é perpendicular ao campo magnético e nula se tem direção paralela ao campo magnético. De forma mais precisa, observa-se que a força é diretamente proporcional a , onde é o ângulo entre a velocidade e o campo magnético.
-
3.
A força sobre diferentes partículas com a mesma velocidade mas com cargas diferentes é diretamente proporcional a e a força sobre partículas de sinais opostos é em sentidos opostos.
-
4.
A direção da força é dada pela regra da mão direita como mostra a figura 7.2, i.e., a força é perpendicular tanto a como a . No caso de uma carga positiva, a força possui o sentido em que aponta o dedo polegar da mão direita quando os outros dedos rodam de para . Ou também, estendendo os dedos polegar, indicador e médio da mão direita, de forma a formarem 90° entre si como os 3 eixos coordenados, se o indicador aponta no sentido de e o dedo médio no sentido de , o sentido da força sobre uma partícula de carga positiva é no sentido em que aponta o polegar. No caso de uma carga negativa, o sentido é o oposto do sentido em que aponta o dedo polegar.
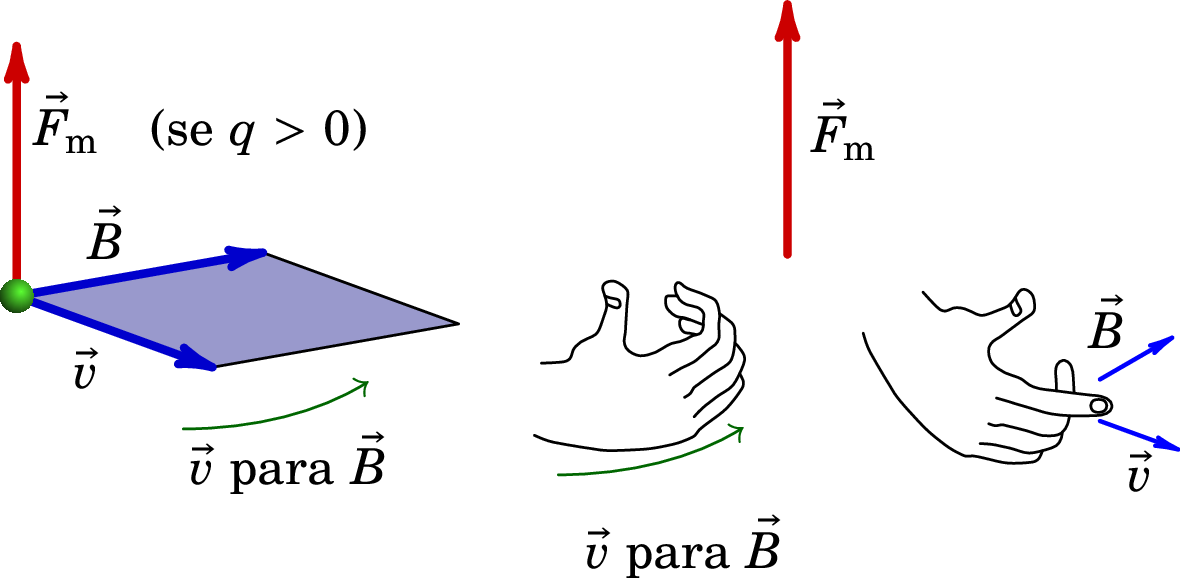
Como o módulo da força magnética é diretamente proporcional a , e , o seu módulo é,
| (7.1) |
onde é a constante de proporcionalidade usada para definir o módulo do campo magnético.
Assim, o campo magnético tem unidades de força sobre carga e sobre velocidade. No Sistema Internacional de unidades usa-se o tesla (T), igual a:
| (7.2) |
Um campo de um tesla é muito forte. Outra unidade usada habitualmente é o gauss (G), definido como:
| (7.3) |
Tendo em conta a expressão (7.1) e a regra da mão direita para definir o sentido da força sobre cargas pontuais, a expressão vetorial da força magnética sobre uma carga pontual é;
| (7.4) |
onde é o produto vetorial dos vetores e . Se a carga for positiva, terá a direção e sentido do produto vetorial ; se a carga for negativa, a força terá a direção de , mas no sentido oposto.
7.2 Força de Lorentz
A força sobre uma partícula pontual de carga , num ponto onde há campo elétrico e campo magnético é dada pela expressão,
| (7.5) |
designada de força de Lorentz. A combinação do campo elétrico e do campo magnético permite produzir movimentos muito variados. Nas sub-secções seguintes, veremos em detalhe os movimentos circular uniforme, helicoidal, retilíneo uniforme e cicloidal.
Em geral, a força de Lorentz pode ter componentes nas direções tangencial e normal da trajetória da partícula (ver figura 7.3). A força magnética é sempre no plano perpendicular à direção tangencial. Qualquer mudança do módulo de , devida à aceleração tangencial, será produzida unicamente pelo campo elétrico, porque o termo , sendo perpendicular a , não tem componente tangencial. A mudança da direção da velocidade, devida à aceleração normal, pode ser originada pelo campo elétrico ou pelo campo magnético, ou por ambos.
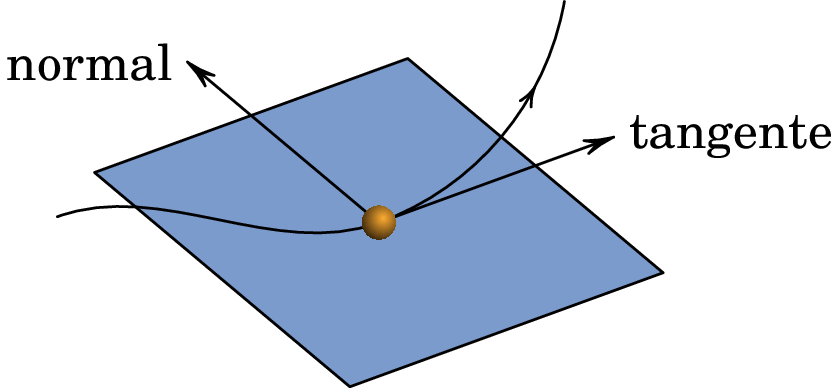
Numa região em que as linhas de campo magnético sejam paralelas, o campo é uniforme. Como é sempre perpendicular à força magnética , e no caso particular deste ser perpendicular a , é por vezes conveniente representar as linhas de campo perpendiculares ao plano da figura, o qual contém os vetores e . Se a linha de campo é no sentido dos nossos olhos para o plano da figura, representa-se com um x, que faz lembrar um seta a afastar-se de nós. Um ponto representa uma linha de campo que é no sentido da figura para os nossos olhos (seta a aproximar-se de nós). Esta representação pode também ser usada noutras situações.
A força de Lorentz pode conduzir a vários tipos de trajetórias diferentes. Nas próximas secções veremos alguns exemplos, admitindo que a velocidade da partícula não seja muito elevada para que possa ser usada a mecânica clássica.
7.2.1 Movimento num campo magnético uniforme
Consideremos uma partícula de carga e massa numa região onde não existe campo elétrico, mas existe campo magnético uniforme. Podemos escolher o eixo na direção e sentido do campo e, como tal, o campo é onde é uma constante. A força magnética em função das componentes cartesianas da velocidade da partícula é:
| (7.6) |
e a segunda lei de Newton () conduz a
| (7.7) |
onde as linhas nas variáveis do lado esquerdo da equação indicam derivada em ordem ao tempo. A equação vetorial anterior é equivalente a 3 equações para as 3 componentes. Para simplificar a resolução destas equações vamos definir uma constante positiva,
| (7.8) |
Vamos admitir primeiramente carga positiva, , e depois de resolvidas as equações discutiremos o caso da carga ser negativa. As 3 equações para as derivadas das componentes da velocidade são:
| (7.9) |
A solução da terceira equação é que a componente permanece constante, igual ao seu valor inicial; para já admitiremos que essa velocidade é nula e mais à frente veremos o caso geral. Para resolver as outras duas equações, deriva-se a primeira em ordem ao tempo, ficando no lado direito que é substituída usando a segunda equação:
| (7.10) |
Esta equação é do mesmo tipo que a equação do oscilador harmónico simples. Por ser uma equação diferencial linear de segunda ordem, têm de existir duas funções diferentes que sejam soluções particulares e a solução geral é a combinação linear dessas duas funções. Neste caso é fácil ver que duas funções diferentes que derivadas duas vezes dão a mesma função inicial multiplicada por são e . A solução geral é portanto dada por:
| (7.11) |
onde e são duas constantes. A solução geral para , de acordo com a primeira equação (7.9), é a derivada de , dividida por :
| (7.12) |
As constantes e encontram-se a partir da velocidade inicial em . Como e , se escolhermos os eixos e de forma que a velocidade inicial tenha apenas componente e não componente , então , e as constantes são , . Escrita de forma vetorial, a solução que encontramos para a velocidade é,
| (7.13) |
observe-se que o módulo da velocidade permanece constante, igual ao seu valor inicial, e que o vetor velocidade roda em sentido horário, com frequência angular constante igual a (equação (7.8)). Isto mostra que o movimento da partícula é um movimento circular uniforme.
Se a carga for negativa então e basta substituir por , o que conduz a movimento circular uniforme no sentido anti-horário.
| (7.14) |
Vemos, deste modo, que as partículas de carga positiva rodam num sentido e as de carga negativa no sentido oposto quando sujeitas ao mesmo campo magnético.
Num campo magnético uniforme todas as cargas pontuais descrevem movimento circular uniforme com frequência angular , denominada por frequência de ciclotrão, porque este tipo de movimento foi aproveitado num dos primeiros aceleradores de partículas chamado ciclotrão. A frequência do movimento circular uniforme é,
| (7.15) |
O período, tempo para completar uma volta, do movimento circular uniforme é dado por . A frequência , igual ao número de voltas completas por unidade de tempo, tem unidades de inverso do tempo. A unidade SI de frequência é o hertz, em homenagem a Heinrich R. Hertz (1857–1894), representada pelo símbolo Hz e equivalente a s. A frequência angular tem unidades de radianos por unidade de tempo: rad/s.
Para determinar o raio das trajetórias circulares, encontraremos a expressão do vetor posição de forma análoga à que foi usada para calcularmos o vetor velocidade. A derivada do vetor posição deverá ser igual à expressão (7.13) do vetor velocidade:
| (7.16) |
equivalente às três equações,
| (7.17) |
A terceira equação acima indica que permanece constante e pode ser escolhido como sendo zero. As primitivas das duas primeiras equações são:
| (7.18) |
em que as constantes e dependem da posição inicial, . Podemos escolher a origem de forma a que a posição inicial seja e, como tal, as duas constantes, e , são nulas. O vetor posição é então:
| (7.19) |
o qual é perpendicular a , expressão (7.13), pois , roda no sentido horário e tem módulo constante, igual ao raio da trajetória circular, dado por:
| (7.20) |
Se a carga for negativa, substituindo por na equação (7.19) fica,
| (7.21) |
em que a origem foi definida de forma a que a posição inicial seja . Note que é perpendicular a , expressão (7.14), roda no sentido anti-horário e tem módulo constante igual a .
A figura 7.4 mostra as trajetórias circulares, no plano , para os casos de carga positiva (esquerda) e negativa (direita).
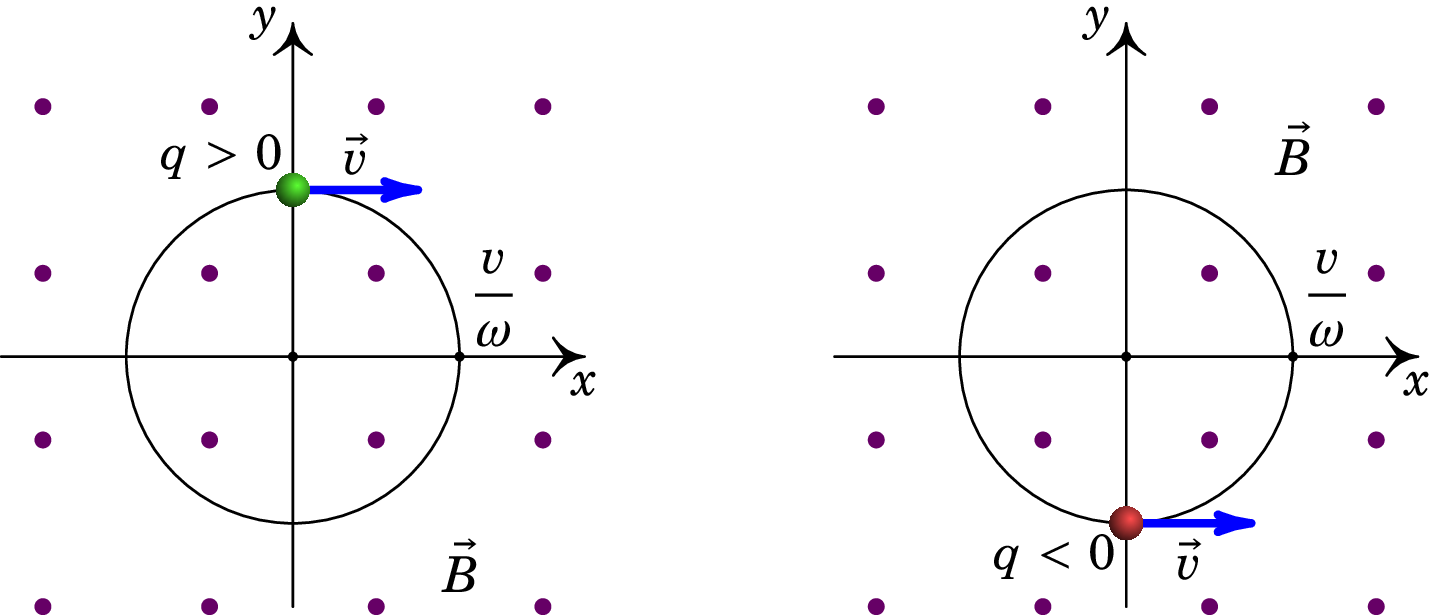
Finalmente, a aceleração da partícula pode ser obtida a partir da expressão (7.7), ou derivando a expressão da velocidade em ordem ao tempo. A aceleração é então dada por:
| (7.22) |
onde é o sinal da carga. Vemos assim, que a aceleração possui sentido oposto ao vetor posição, é perpendicular à velocidade , possui apenas componente normal (apontando para dentro da trajetória) e tem módulo constante igual a , como deve ser num movimento circular uniforme.
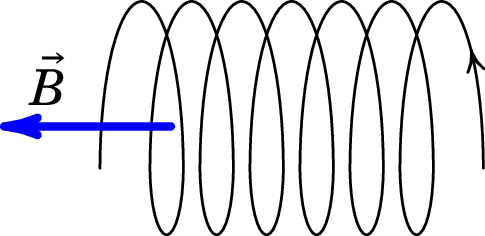
Se a componente da velocidade inicial não for nula, como essa componente permanece constante, o movimento será a sobreposição do movimento circular uniforme, com frequência angular e raio igual à componente da velocidade no plano dividida por , mais o movimento uniforme na direção . A trajetória resultante é uma hélice (ver figura 7.5), com eixo paralelo ao campo magnético, em que a partícula roda com a frequência angular de ciclotrão (equação (7.8)) enquanto se desloca no sentido do campo com velocidade constante (componente da velocidade paralela ao campo). A hélice envolve um cilindro com raio igual ao raio do movimento circular na projeção no plano perpendicular ao campo:
| (7.23) |
onde é a componente da velocidade perpendicular ao campo: , sendo o ângulo entre e .
Num campo magnético não uniforme, as partículas com carga descrevem hélices em torno das linhas de campo magnético, com frequência maior e raio menor nas regiões onde o campo é mais forte. Na atmosfera terrestre, as partículas dos raios cósmicos seguem as linhas de campo magnético terrestre até aos polos magnéticos, onde chocam entre si dando origem às auroras boreais no polo norte e às auroras austrais no polo sul.
Exemplo 7.1
Em vários dispositivos em que são aceleradas partículas usando uma diferença de potencial, e.g., osciloscópios e microscópios eletrónicos, as partículas que passam por um pequeno orifício (O na figura) após serem aceleradas, têm todas a mesma componente da velocidade ao longo do eixo , mas podem ter também uma componente da velocidade perpendicular ao eixo , formando um feixe que diverge do ponto O. Todas as partículas têm a mesma massa e a mesma carga . Para focar o feixe num ponto a uma distância da origem O, usa-se um campo magnético uniforme, na direção do eixo . Mostre que de facto o feixe converge e encontre o módulo do campo magnético para que o ponto onde convergem esteja à distância da origem.
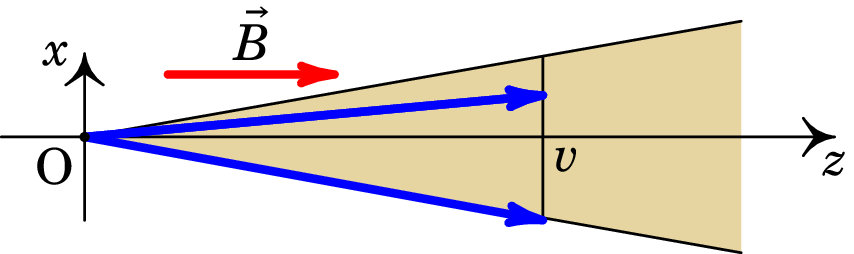
Resolução. Dependendo da componente perpendicular da velocidade, as partículas seguem por hélices diferentes. Mas como a frequência angular de ciclotrão (equação (7.8)) não depende da velocidade, todas as partículas rodam nas hélices com a mesma frequência e o mesmo período:
Após completarem cada volta na hélice, as partículas passam novamente pelo eixo . Como a componente da velocidade de cada partícula permanece constante, a posição onde uma partícula completa a sua primeira volta é essa componente da velocidade vezes o período:
que é igual para todas as partículas no feixe. Como tal, todas as partículas convergem no eixo após o tempo (e , , etc.). Para que esse ponto esteja à distância da origem, o valor do módulo do campo magnético deverá ser:
(poderia ser também o dobro, o triplo, etc.).
A figura seguinte mostra o movimento de três partículas que passam por O: a partícula 1 com componente perpendicular da velocidade inicial no sentido negativo do eixo , a partícula 2 sem velocidade perpendicular a e a partícula 3 com componente perpendicular da velocidade inicial no sentido positivo do eixo .
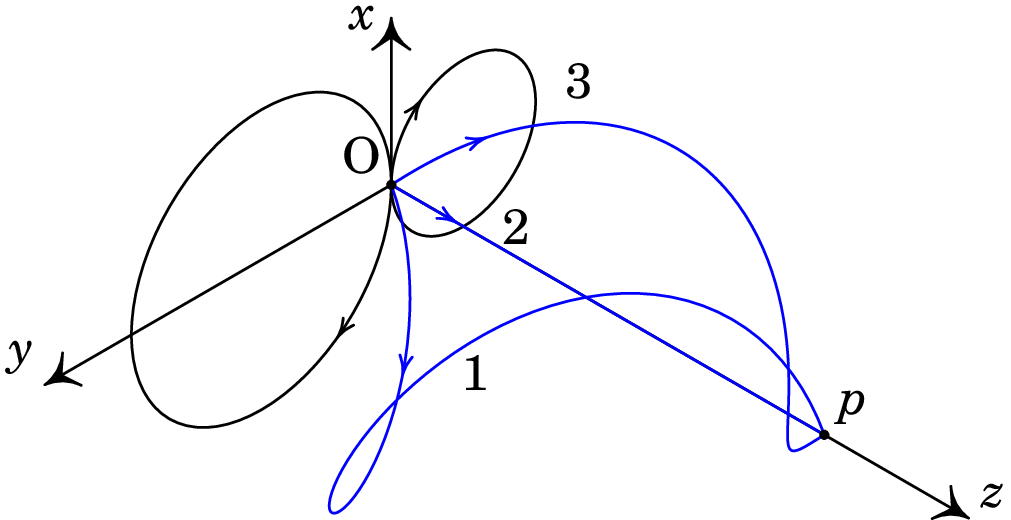
A figura mostra também as projeções dos movimentos das partículas 1 e 3 no plano , perpendicular ao campo magnético, que são círculos com raios diferentes.
7.2.2 Espetrómetro de massa
Uma aplicação prática do movimento circular de partículas num campo magnético uniforme é o espetrómetro de massa, usado para determinar a massa atómica das moléculas que compõem um gás. A figura 7.6 ilustra o espetrómetro inventado por Arthur J. Dempster, em 1918.
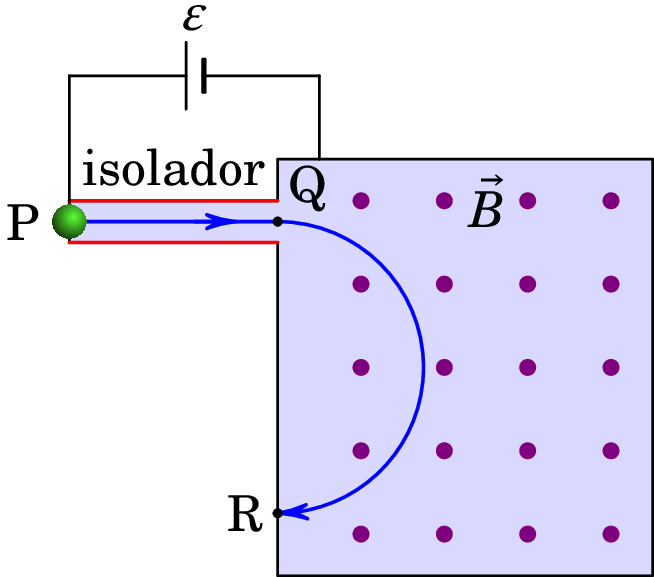
O espetrómetro da figura 7.6 é um contentor hermético e com vácuo, composto por um tubo isolador, entre os pontos P e Q, e uma caixa metálica. Os átomos ou moléculas são ionizados e inseridos no ponto P. Entre o ponto P e a caixa metálica liga-se uma f.e.m. que acelera os iões, de carga postiva, no tubo isolador até à entrada da caixa no ponto Q. No interior da caixa metálica (condutor fechado) não existe campo elétrico, mas há campo magnético uniforme , perpendicular à trajetória dos iões e com módulo que pode ser ajustado até que os iões com uma determinada massa descrevam a trajetória semi-circular entre Q e R, sendo depois detectados num medidor de corrente iónica em R.
Admitindo que os iões partem do repouso em P, a energia cinética com que entram na caixa é igual à perda de energia potencial elétrica entre P e Q,
| (7.24) |
Tendo em conta que a distância é duas vezes o raio da trajetória semi-circular, usando a expressão (7.23), a relação entre a velocidade de um ião na caixa metálica e o campo magnético é,
| (7.25) |
Combinando as equações (7.24) e (7.25), obtém-se a massa de um ião de carga em função dos parâmetros do espetrómetro e do módulo do campo magnético:
| (7.26) |
No caso dos átomos ou moléculas ionizados possuirem carga elétrica negativa, de modo a estes descreverem a mesma trajetória da figura 7.6, então a polaridade da f.e.m. deve invertida e o sentido do campo magnético também tem de ser invertido, sendo que a expressão (7.26) permanece válida substituindo-se neste caso por .
7.2.3 Campos perpendiculares e uniformes
No caso em que há campos elétrico e magnético, ambos uniformes e perpendiculares entre si, podemos definir o eixo na direção e sentido do campo magnético e o eixo na direção e sentido do campo elétrico. A força de Lorentz (7.5) em função das componentes cartesianas da velocidade da partícula com carga é:
| (7.27) |
Um caso simples é quando a velocidade inicial da partícula é:
| (7.28) |
o que faz com que a força seja nula e, como tal, o movimento é retilíneo e com velocidade constante. Este resultado é usado num dispositivo chamado filtro de velocidades. Trata-se de selecionar as partículas com um valor específico da velocidade, num feixe de partículas todas com velocidade na mesma direção, mas com módulos diferentes.
Estabelece-se um campo elétrico uniforme, de módulo , perpendicular à velocidade das partículas, e um campo magnético uniforme perpendicular à velocidade das partículas e ao campo elétrico, com módulo tal que seja igual ao valor da velocidade que vai ser selecionada (ver figura 7.7).
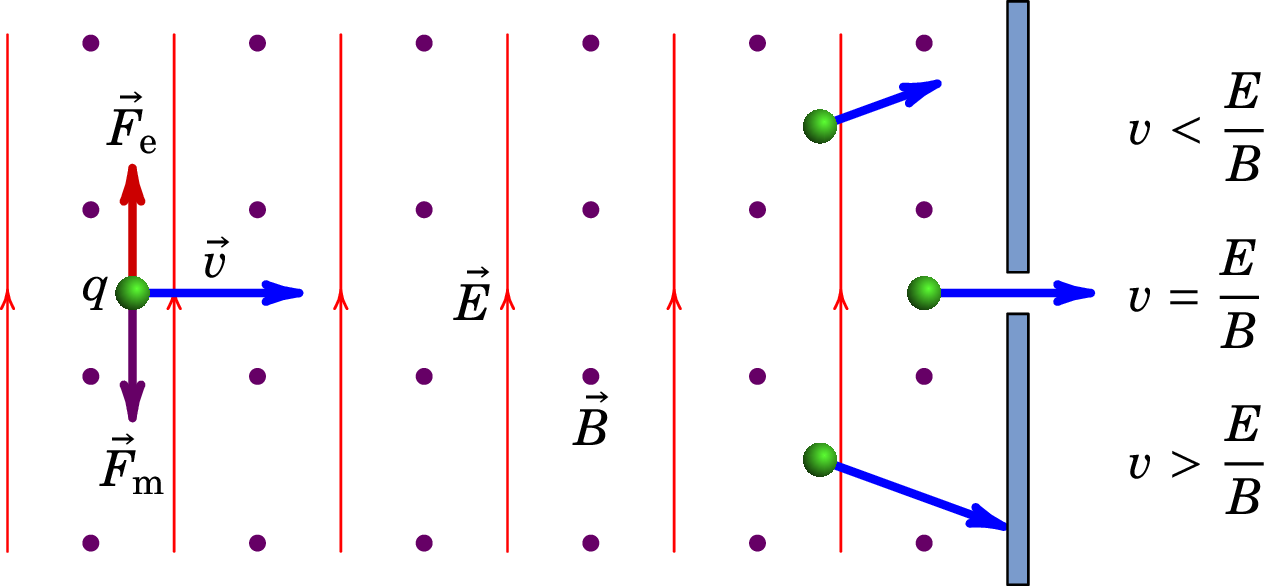
Coloca-se uma barreira no filtro, de maneira que unicamente as partículas que se deslocam em linha reta (com velocidade em módulo igual a ) logrem ultrapassar a barreira. As partículas com outras velocidades diferentes seguirão uma trajetória curva; as cargas representadas na figura são positivas, de maneira que se a velocidade for superior a , a força magnética, para baixo, é superior à força elétrica, para cima; e se a velocidade for menor que , a força elétrica, para cima, é superior à força magnética, para baixo.
Admitiremos primeiro que é positiva () e usaremos a definição (7.8) da frequência de ciclotrão. Partindo da expressão (7.27) e usando a segunda lei de Newton (), o vetor aceleração da partícula é dado por:
| (7.29) |
As três equações diferenciais das componentes da velocidade são portanto:
| (7.30) |
A solução geral das equações (7.30) é obtida usando o mesmo método usado na secção 7.2.1. Deriva-se a primeira equação em ordem ao tempo e substitui-se usando a segunda equação:
| (7.31) |
Com a substituição , a equação diferencial obtida para é a mesma equação (7.10) com a mesma solução geral (7.11), mas para em vez de . A componente obtém-se derivando e dividindo por . Como tal, a solução geral das equações (7.30) é:
| (7.32) |
onde , e são três constantes que dependem da velocidade inicial.
No caso da partícula possuir velocidade inicial , então e a velocidade permanece constante. O vector posição, considerando como posição inicial a origem, é então dado por . Este caso corresponde ao movimento retilíneo uniforme anteriormente referido, no qual a partícula não é defletida pela presença dos campos elétrico e magnético (ver figura 7.7). De salientar que este resultado é independente do valor da carga das partículas, i.e., do seu módulo e do seu sinal.
Um caso interessante ocorre quando a partícula parte do repouso, para o qual e . O movimento é então no plano e as componentes da velocidade são,
| (7.33) |
O vetor velocidade pode-se escrever como a soma de duas velocidades; no caso :
| (7.34) |
O primeiro termo corresponde a translação no sentido positivo de , com velocidade uniforme , e o segundo termo é uma rotação no sentido horário, com frequência angular constante e velocidade de módulo constante , tal como o movimento circular uniforme descrito pela expressão (7.13). O movimento da partícula é portanto a composição de um movimento de translação com um movimento de rotação. Como os módulos das velocidades de translação e rotação são iguais em módulo, o movimento é então semelhante ao movimento de um ponto na periferia de uma roda que se desloca para a direita com velocidade . Em relação ao eixo da roda, o ponto roda no sentido horário, com velocidade tangencial , enquanto o eixo da roda se desloca para a direita com velocidade . Nos instantes em que o ponto toca o chão, a sua velocidade é nula; a seguir o ponto acelera e tem velocidade máxima, , para a direita, quando estiver mais afastado do chão. A trajetória resultante é um cicloide (ver figura 7.8). As coordenadas da posição da partícula em função do tempo são as primitivas das expressões (7.33) e as constantes de integração podem ser definidas de forma a que a posição inicial seja a origem:
| (7.35) |
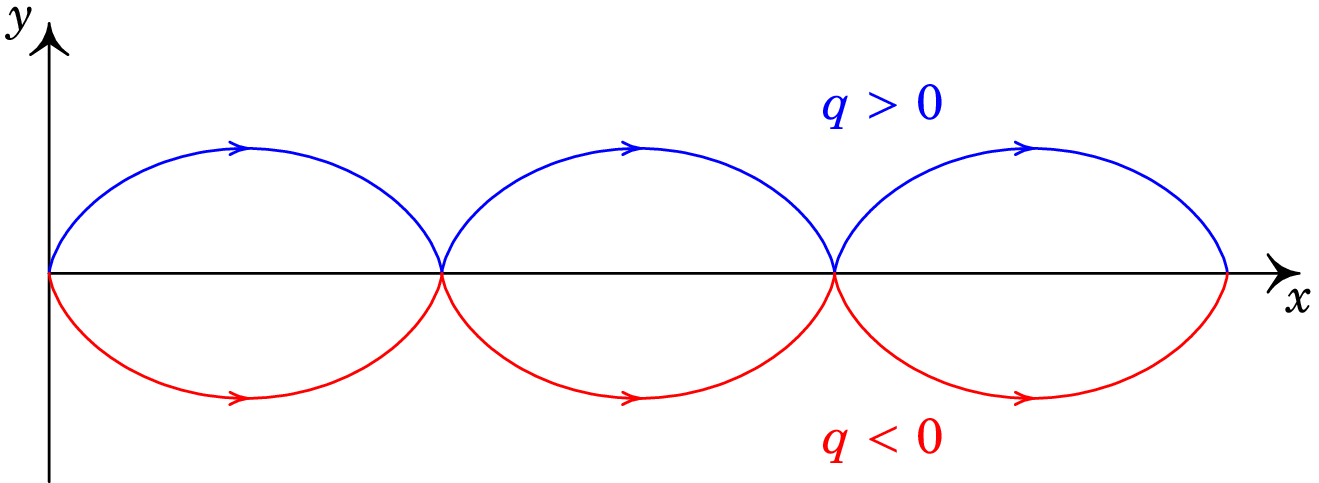
Para o caso no qual a carga é negativa então , o que implica substituir por . A velocidade da partícula é então dada por:
| (7.36) |
e as componentes do vetor posição por:
| (7.37) |
De notar que a velocidade e a posição iniciais se mantêm nulas. A diferença em relação ao movimento cicloidal de uma partícula de carga positiva é que agora o movimento cicloidal possui rotação no sentido oposto, i.e., no sentido anti-horário (ver figura 7.8).
O movimento pode também ser compreendido da seguinte forma. Como a partícula possui velocidade inicial nula, a força magnética inicial é nula e a força elétrica acelera a partícula segundo o eixo . A velocidade passa então a ser não nula e a força magnética faz a partícula rodar em torno das linhas de campo magnético (ver figura 7.4), enquanto que a força elétrica continua a provocar aceleração segundo o eixo . O movimento é pois uma combinação dos dois efeitos produzidos pelas forças elétrica e magnética. Resolvidas as equações de movimento, verifica-se que a partícula possui movimento cicloidal (ver figura 7.8).
7.3 Força magnética sobre condutores com corrente
Quando um condutor, que transporta corrente, se encontra numa região onde existe um campo magnético, o movimento das suas cargas de condução dá origem a forças magnéticas que atuam sobre o próprio condutor (ver figura 7.9).
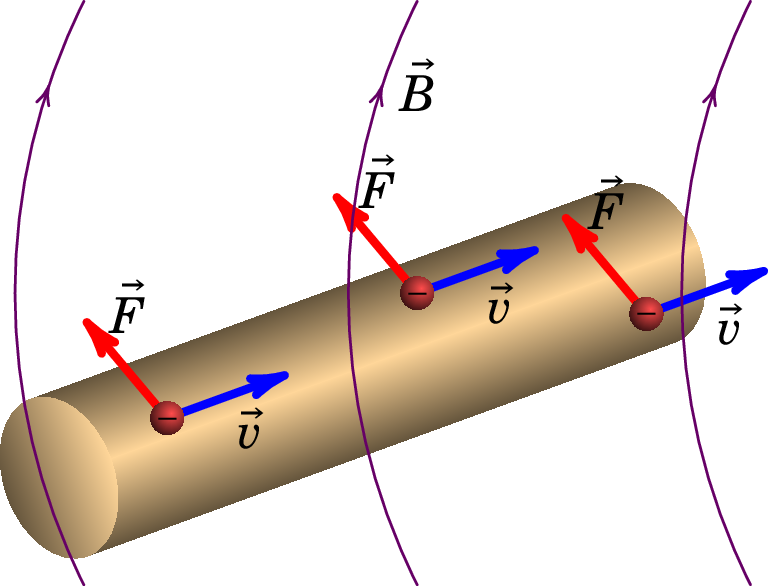
A força magnética média sobre cada carga de condução do condutor é o produto vetorial do vetor velocidade média das cargas de condução pelo campo magnético a que estão sujeitas, multiplicado pelo valor de cada carga. O elemento infinitesimal de força magnética sobre um comprimento infinitesimal de fio , possuindo um número infinitesimal de cargas de condução , é então dado por:
| (7.38) |
Como é um comprimento infinitesimal, pode-se admitir que o campo é constante neste. A carga total de condução no comprimento infinitesimal de fio, , é igual ao produto da densidade volúmica de cargas de condução, , pelo volume do comprimento infinitesimal de fio:
| (7.39) |
onde é a área da secção transversal do fio. Como tal, temos que:
| (7.40) |
sendo que produto é o valor médio da densidade de corrente elétrica, , cujo módulo multiplicado pela área da secção transversal, , é igual ao valor da corrente elétrica que percorre o fio.
O vetor deslocamento infinitesimal ao longo do fio possui módulo igual a e é tangente ao fio, possuindo portanto a direção e o sentido do vetor densidade de corrente elétrica , ou seja, , onde é o versor do vetor densidade de corrente elétrica. Assim, o elemento infinitesimal de força magnética, expressão (7.40), em função da corrente e do vetor deslocamento infinitesimal, escreve-se como:
| (7.41) |
A força magnética total sobre o fio obtém-se integrando a força infinitesimal, expressão (7.41), ao longo do fio entre a sua extremidade inicial A e a sua extremidade final B. Tendo em conta que a intensidade da corrente é constante ao longo do fio, obtemos então que:
| (7.42) |
No caso do campo ser uniforme, obtém-se:
| (7.43) |
De salientar que as expressõe (7.42) e (7.43) são válidas qualquer que seja a forma geométrica do fio condutor. No caso particular de um fio retilíneo de comprimento percorrido por uma corrente elétrica constante e sujeito a um campo uniforme, então e a força magnética sobre o fio é dada por:
| (7.44) |
onde o vetor corrente elétrica é dado por , possuindo módulo igual à corrente elétrica e a direção e o sentido desta. Observe-se que a força magnética sobre o fio, expressão (7.44), possui módulo dado por:
| (7.45) |
onde é o ângulo entre o campo magnético e o fio. Vemos pois que quando o campo magnético é paralelo ao fio a força magnética é nula e que quando o campo é perpendicular ao fio a força magnética é máxima.
Exemplo 7.2
Uma espira retangular por onde circula corrente de intensidade , no sentido indicado na figura, tem uma aresta de comprimento dentro de uma região onde há campo magnético uniforme, de módulo , para dentro da figura. Na aresta oposta, fora da região com campo, está pendurado na vertical um objeto de massa . Que valor deverá ter a intensidade da corrente para que o sistema esteja em equilíbrio?
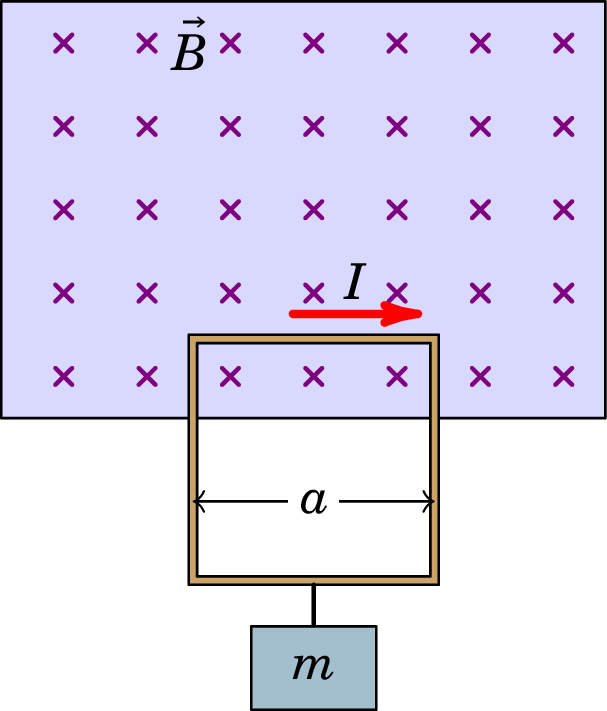
Resolução. Usando a equação (7.44) para fios retilíneos, a força magnética na aresta de comprimento dentro do campo aponta para cima e tem módulo,
Para equilibrar o peso do objeto, , para baixo, a corrente deverá ser:
Nas partes das duas arestas verticias da espira que estão dentro da região onde existe campo magnético também há força magnética na direção horizontal; as forças nestas duas partes possuem o mesmo módulo e como são opostas anulam-se.
7.4 Momento magnético
Uma espira tal como a do exemplo 7.2, é um fio condutor que forma um circuito fechado e por onde pode circular corrente, por exemplo, a espira circular no lado esquerdo da figura 7.10. O fio não é completamente fechado, mas em alguns pontos terá uma entrada e uma saída, ligadas a uma fonte que fornece a corrente. No entanto, será representada como se fosse um circuito fechado com corrente a circular por ele. Um fio condutor enrolado em várias voltas é uma bobina, tal como a bobina cilíndrica no lado direito da figura 7.10. Pode-se considerar como se cada volta fosse uma espira, todas elas com a mesma corrente.

Na espira do exemplo 7.2 há força magnética para cima, porque uma das arestas está fora da região onde existe campo magnético. Se a espira estiver completamente dentro da região onde há campo magnético uniforme, as forças magnéticas nas arestas anulam-se e a força magnética resultante é zero. De facto, este resultado é geral para um fio condutor fechado com uma forma geométrica qualquer percorrido por uma corrente constante e sujeito a um campo magnético uniforme. Usando a expressão (7.43) e notando que para um percurso fechado temos (a adição de todos os deslocamentos infinitesimais ao longo de um percurso fechado é nula), conclui-se que a força magnética total é nula. Como a força total é nula então o centro de massa do percurso fechado permanece fixo, i.e., não há movimento de translação.
No entanto, existe um binário magnético não nulo que faz rodar a espira; para calcular este binário, consideremos a espira retangular da figura 7.11, dentro de uma região onde há campo magnético uniforme de baixo para cima, no mesmo plano da aresta.
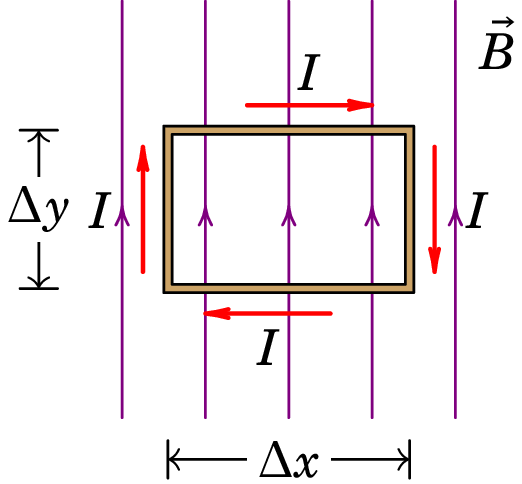
As forças magnéticas nas duas arestas laterais (esquerda e direita) são nulas. Na aresta de cima atua uma força magnética para fora da figura e na aresta de baixo atua uma força magnética com o mesmo módulo, mas para dentro da figura. Como estas forças são iguais em módulo e possuem sentidos opostos, a sua soma é nula. As suas linhas de ação são paralelas, afastadas uma da outra e não passam pelo centro da espira, produzindo assim um binário que faz rodar a espira de forma que a aresta de cima desloca-se para fora do plano da figura e a aresta de baixo desloca-se para dentro do plano da figura. O módulo de cada uma dessas forças é,
| (7.46) |
E o momento do binário, igual ao módulo das forças opostas vezes a distância entre as suas linhas de ação, é:
| (7.47) |
o produto é igual à área da espira.
A rotação da espira faz diminuir a distância entre as linhas de ação das forças para , em que é o ângulo que a espira rodou. O momento do binário é agora,
| (7.48) |
Define-se o versor normal da espira, perpendicular ao seu plano e no sentido da regra da mão direita segundo o sentido da corrente. Na espira da figura 7.11 a direção da corrente implica que o versor normal é para dentro da figura. O ângulo que o plano da espira roda em relação às linhas de campo, implica um ângulo entre o versor normal e o campo magnético. Como , então . E o momento do binário magnético escreve-se de forma vetorial como:
| (7.49) |
onde o vetor , denominado por momento magnético da espira, tem módulo igual ao produto da sua área vezes a intensidade da corrente e direção do versor normal:
| (7.50) |
De referir que, quando a espira roda, surgem forças nas duas arestas laterais (esquerda e direita), as quais são iguais em módulo e de sentidos opostos. Estas forças anulam-se e como se encontram na mesma linha de ação, a qual passa pelo centro da espira, o seu momento de binário é nulo.
Uma espira com qualquer forma e tamanho pode ser aproximada pela soma de várias espiras retangulares infinitesimais, com as da figura 7.11. Como tal, a expressão (7.50) do momento magnético é geral para qualquer tipo de espira plana e o momento de binário quando a espira for colocada num campo magnético uniforme é dado pela equação (7.49). O momento magnético é perpendicular ao plano da espira e na direção da regra da mão direita segundo o sentido da corrente, como mostra a figura 7.12: o polegar da mão direita define o sentido de , quando os outros quatro dedos rodam no sentido da corrente na espira.

Resumindo um campo magnético uniforme não produz nenhuma força sobre uma espira condutora com corrente elétrica, mas produz binário que faz rodar a espira, em torno do seu centro de massa. O campo magnético exterior faz rodar a espira e o seu momento magnético de modo a este ficar com a direção e o sentido de . Este facto encontra-se em analogia com o momento do binário elétrico que atua num dipolo elétrico sujeito a um campo elétrico exterior, o qual faz rodar o dipolo e o seu momento dipolar de modo a este ficar com a direção e o sentido do campo elétrico exterior (ver problema 1.14 do capítulo 1).
O momento magnético de uma bobina é a soma dos momentos magnéticos de todas as suas espiras. Se a bobina tiver espiras, todas com a mesma área , o seu momento magnético é .
A equação (7.49) pode ser generalizada para o caso em que o campo magnético não é uniforme, dividindo a espira em pequenos pedaços com momento magnético infinitesimal e admitindo que o campo em cada espira infinitesimal é constante; a soma de todas as contribuições conduz ao momento do binário total igual ao integral de na superfície delimitada pela espira:
| (7.51) |
O momento do binário produzido pelo campo magnético é o princípio usado nos motores elétricos. A figura 7.13 mostra um mostor de corrente contínua. A bobina do motor está fixa a um eixo que lhe permite rodar e é atravessada por um campo magnético produzido por ímanes fixos. Os dois terminais da bobina ligam-se a um comutador que roda juntamente com a bobina. O comutador é um cilindro com dois setores metálicos isolados a fazer contato com os dois terminais e ligados a uma f.e.m. No instante mostrado a figura, terminais positivo e negativo produzem corrente na direção que faz com que o momento magnético da bobina aponte para cima.
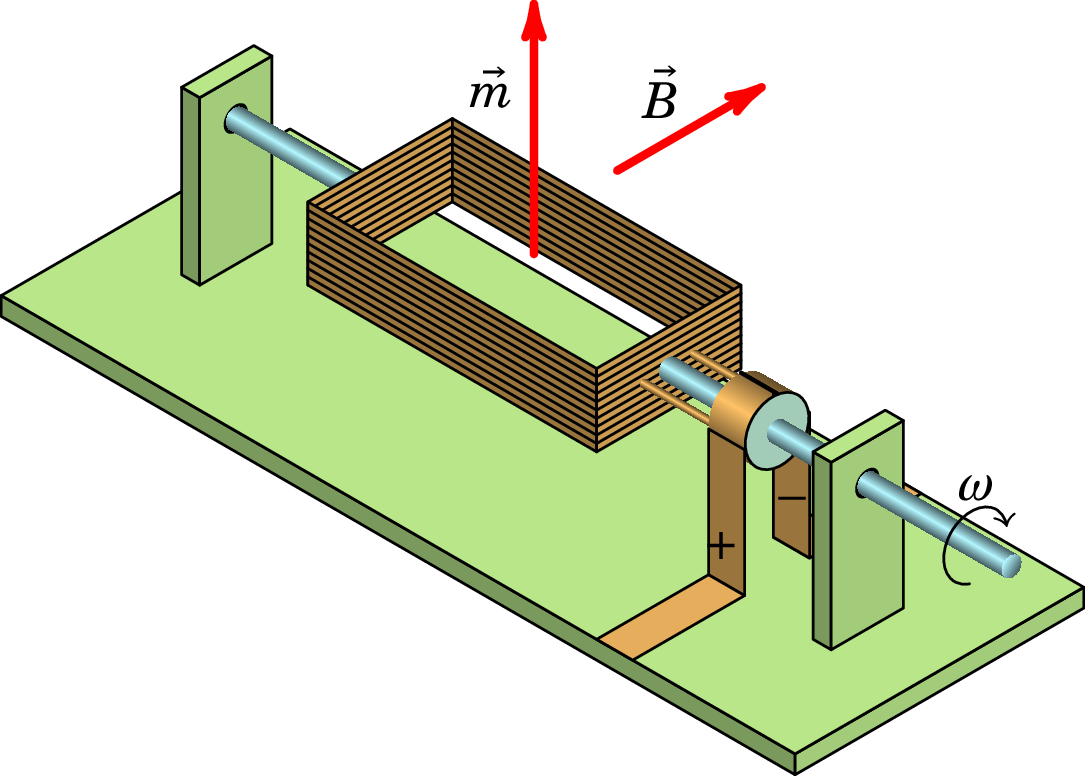
Como o campo magnético aponta para o lado, a bobina roda com a velocidade angular no sentido indicado. Quando a bobina roda até à posição em que aponta para o lado direito, na mesma direção do campo , o momento de binário é zero nessa posição. Nesse momento os terminais positivo e negativo ficam em contacto com as duas separações entre os sectores do comutador deixando de passar corrente pela bobina e o momento magnético é nulo. Mas por inércia a bobina roda mais um pouco, de forma que os terminais positivo e negativo voltam a fazer contacto com os sectores metálicos do comutador, mas agora houve uma troca dos sectores; como tal, agora a corrente circula no sentido inverso e troca de sentido apontando para a esquerda. Volta a aparecer momento de binário que faz rodar no sentido de e assim continua a rotação no mesmo sentido.
Exemplo 7.3
Uma espira retangular com lados de 25 cm e 30 cm, transporta uma corrente de 2.5 A, no sentido indicado na figura. A espira encontra-se num plano vertical que faz um ângulo de 30° com o plano O e existe um campo magnético uniforme (SI). Calcule o momento do binário produzido pelo campo magnético sobre a espira e diga em que sentido rodará a espira.
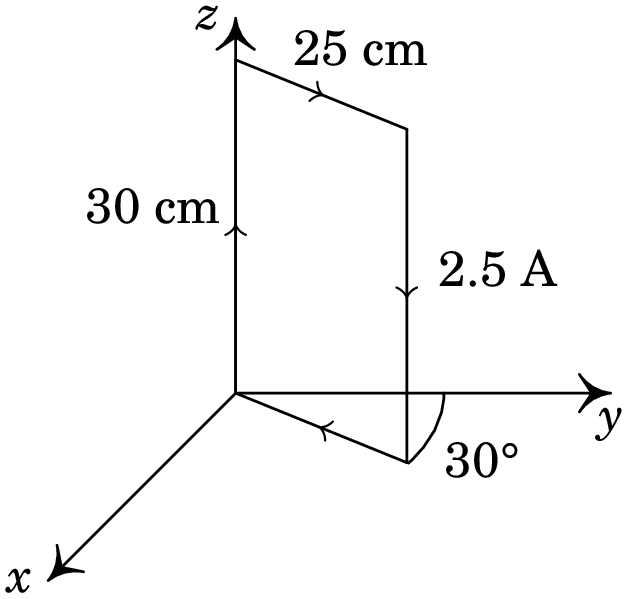
Resolução. A área da espira é:
Usando a regra da mão direita, vê-se que o momento magnético da espira é paralelo ao plano O com o sentido indicado na figura seguinte:
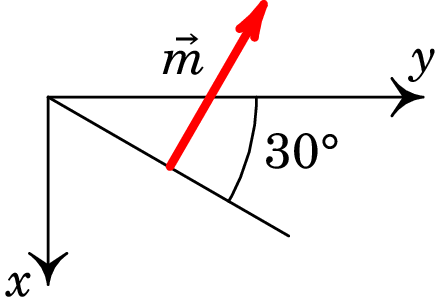
Como tal, o versor normal é:
e o momento magnético da espira é:
O momento do binário é igual ao produto vetorial entre o momento magnético da espira e o campo magnético:
A direção de significa que a espira roda com o sentido oposto ao dado pela regra da mão direita em relação ao eixo , até o seu momento magnético apontar na direção e no sentido do campo magnético. Consequentemente, a bobina roda em torno de um eixo paralelo ao eixo , que passa pelo seu centro de massa, de forma a que o ângulo inicial de 30° aumente até 90°.
Problemas
-
7.1.
Um protão (massa kg) encontra-se na origem, em , com velocidade (km/s), dentro de uma região onde há vácuo e campo magnético uniforme: (T). Determine a posição do protão em µs.
-
7.2.
Um protão "navega"na atmosfera solar, a uma velocidade de , onde é a velocidade da luz no vazio ( m/s). O protão atravessa um campo magnético uniforme de 0.12 T, formando um ângulo de 25° com a sua velocidade. Calcule o raio do cilindro que envolve a órbita helicoidal do protão (a massa de um protão é kg e admita que com a velocidade os efeitos relativistas são desprezáveis).
-
7.3.
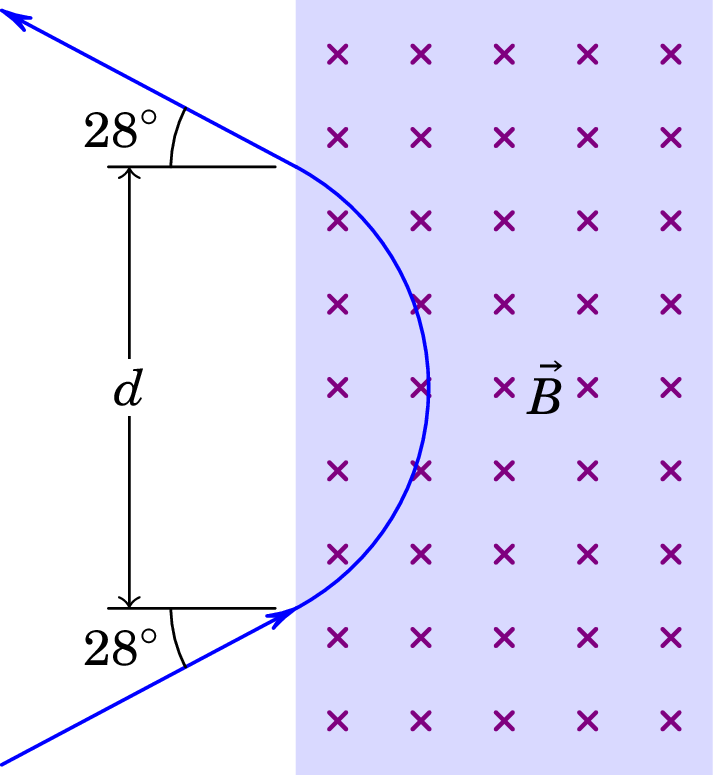
Um protão desloca-se no vácuo, com velocidade de m/s, entrando numa região retangular onde existe campo magnético constante , perpendicular à sua velocidade, como mostra a figura. No ponto onde o protão penetra o campo magnético, a sua velocidade faz um ângulo de 28° com a fronteira do retângulo. Após a trajetória circular dentro do campo magnético, o protão sai do retângulo com velocidade que faz novamente um ângulo de 28° com a fronteira do retângulo. Sabendo que o módulo do campo magnético é 0.64 T, e a massa do protão é kg, determine a distância entre os pontos onde o protão entra e sai do retângulo onde existe campo magnético.
-
7.4.
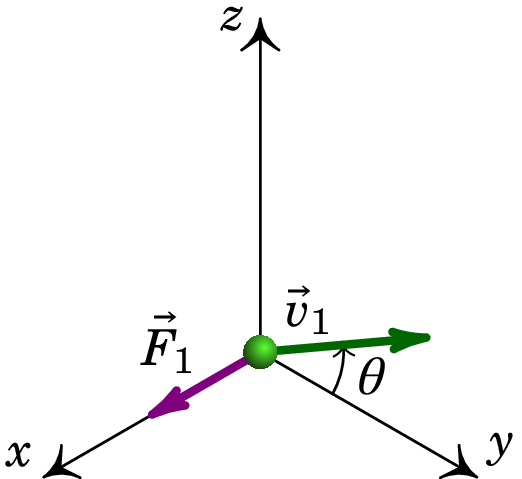
Uma partícula com carga de nC encontra-se numa região onde existe campo magnético uniforme . Quando se move com velocidade , no plano e fazendo um ângulo com o eixo dos , tal como mostra a figura, a força magnética sobre ela é , na direção e sentido do eixo dos . Quando a velocidade da partícula é m/s, a força magnética sobre ela é µN. Determine o campo .
-
7.5.
A espira triangular na figura tem um vértice na origem, o vértice P no eixo dos , a 30 cm da origem, e o vértice Q no eixo dos , a 40 cm da origem. Existe um campo magnético uniforme (em teslas) e na espira circula corrente de intensidade mA, no sentido indicado na figura.
(a) Determine a força magnética sobre cada um dos três lados da espira.
(b) Determine a força magnética total sobre a espira.
(c) Determine o momento do binário magnético sobre a bobina.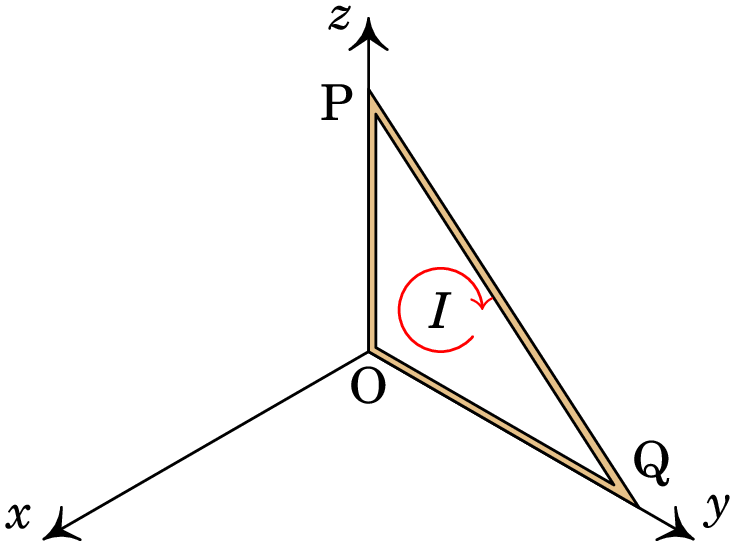
-
7.6.
Num filtro de velocidades há campos elétrico e magnético uniformes e perpendiculares, e as partículas entram com velocidade perpendicular aos dois campos. O módulo do campo magnético é 0.1 T e o do campo elétrico 0.2 MV/m.
(a) Qual a velocidade das partículas à saída do filtro, i.e., das partículas que não são desviadas na sua passagem pelo filtro?
(b) Qual a energia de um protão à saída do filtro?
(c) Qual a energia de um eletrão à saída do filtro? (A massa de um protão e do eletrão encontram-se no apêndice C.) -
7.7.
Calcule a intensidade máxima do momento do binário magnético que atua sobre uma bobina circular de 400 espiras de raio 0.1 cm, percorrida por uma corrente de 92 mA, num campo magnético uniforme de 0.3 T.
-
7.8.
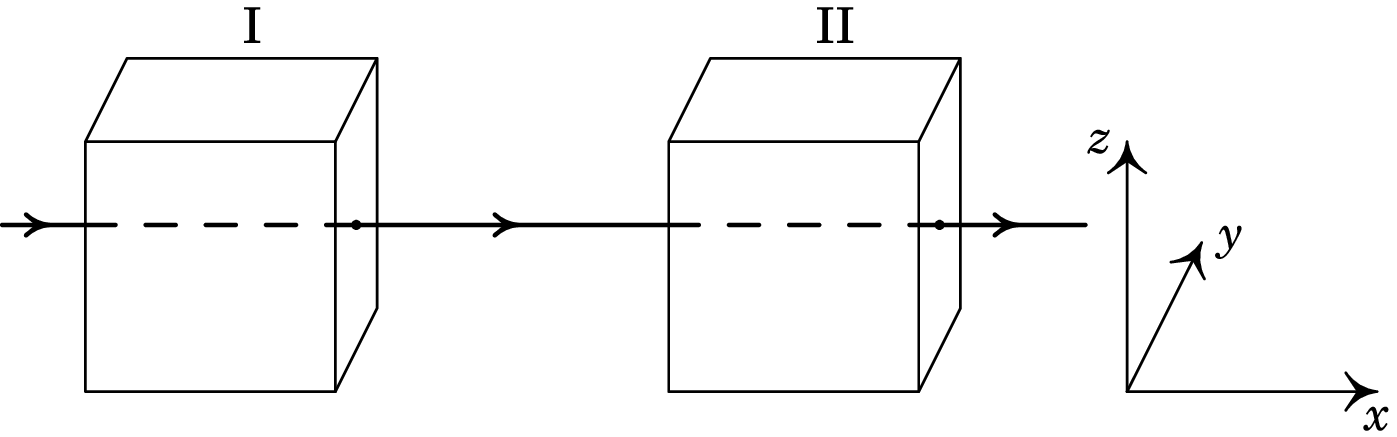
Um feixe de protões desloca-se com velocidade constante segundo o eixo , atravessando duas regiões, I e II, caracterizadas do seguinte modo: na região I existe um campo magnético e na região II coexistem um campo magnético e um campo elétrico . Todos os campos são uniformes nas regiões em que foram definidos e anulam-se fora delas. O peso dos protões não é significativo. Quais as condições a que devem obedecer os campos e para que o feixe não sofra qualquer perturbação no seu movimento, enquanto atravessa duas regiões? Se em vez de protões, fosse um feixe de eletrões, as condições estabelecidas manter-se-iam?
-
7.9.
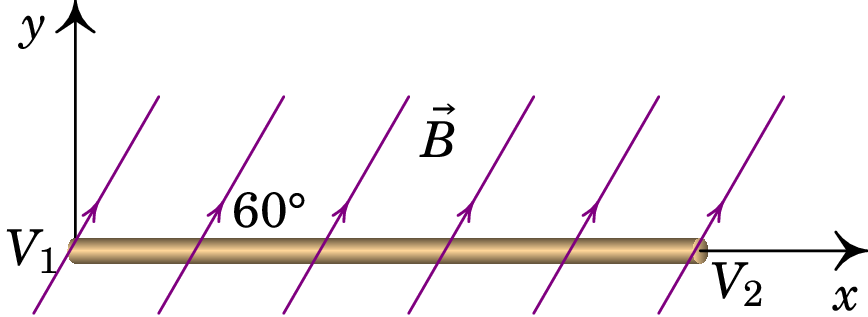
Um fio linear de cobre, de diâmetro 2.59 mm e de comprimento 2 m, encontra-se dentro de um campo magnético uniforme ( G) que faz um ângulo de 60° com o fio. Calcule a força magnética sobre o fio quando se aplica uma diferença de potencial de 0.06 V entre os seus extremos.
-
7.10.
Partículas de carga e massa são aceleradas, a partir do repouso, por uma diferença de potencial e entram numa região de campo magnético uniforme de módulo perpendicular à velocidade. Sendo o raio de curvatura das órbitas circulares, mostre que é igual a .
-
7.11.
Um fio retilíneo com 2 m de comprimento encontra-se ao longo do eixo , centrado na origem. A corrente através do fio é de 5.0 A na direção e sentido de . Se a força magnética sobre o fio, devida a um campo magnético uniforme, for (unidades SI), determine o campo magnético .
-
7.12.
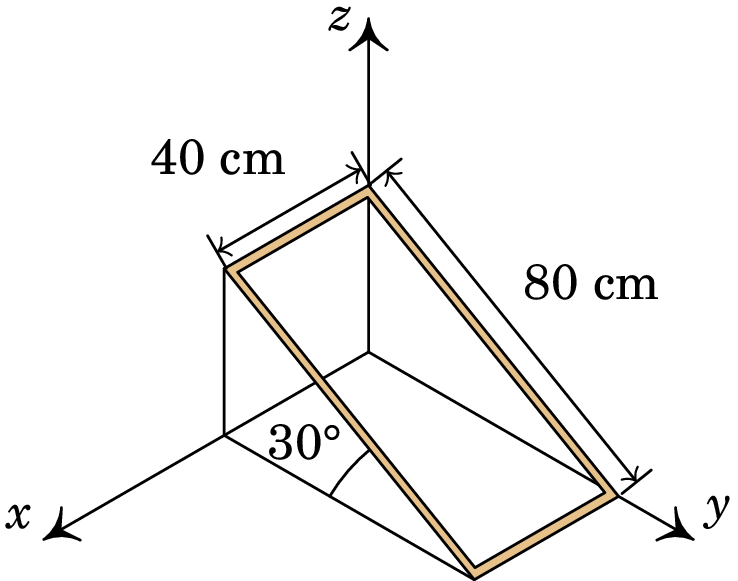
A espira retangular na figura, com arestas de 40 cm e 80 cm, está inclinada 30° em relação ao plano e é percorrida por uma corrente de 0.25 A no sentido indicado na figura. Determine o momento do binário na espira, quando o campo magnético é uniforme, na direção e sentido do eixo , com módulo de 1.8 T e interprete o resultado.
-
7.13.
Em 1879, o físico E. H. Hall descobriu que quando uma corrente elétrica atravessa uma lâmina metálica de largura , sujeita a um campo magnético que lhe é perpendicular, surge uma distribuição não homogénea de carga na direção perpendicular à corrente e ao campo magnético, a qual se traduz numa diferença de potencial entre os lados inferior e superior da lâmina, denominada por tensão de Hall, como se mostra na figura; este fenómeno designa-se por efeito Hall. A importância desta experiência é que pela primeira fez foi possível determinar o sinal de cargas de condução.
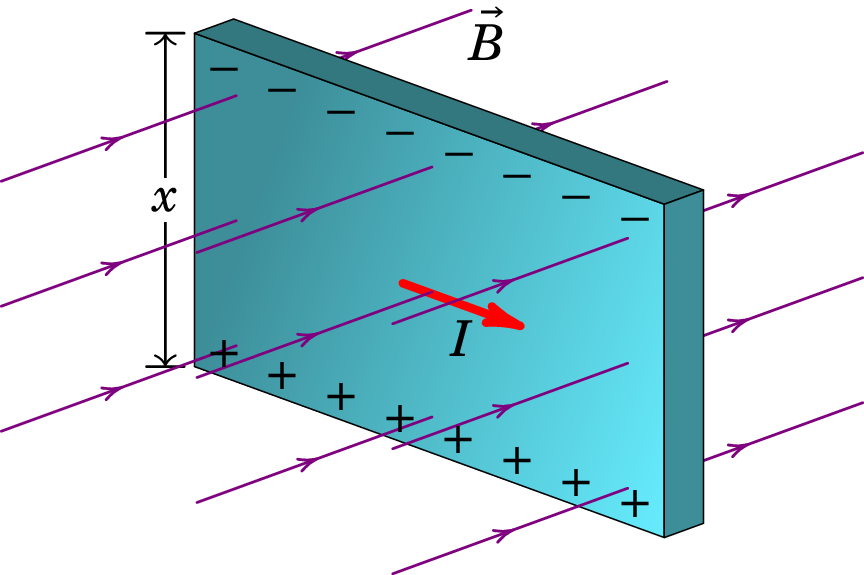
(a) Calcule a força magnética inicialmente sentida pelos portadores de carga quando se movem na lâmina e explique o aparecimento da distribuição não homogénea de carga.
(b) Quando o estado estacionário é atingido, mostre que , em que é a densidade volúmica de cargas de condução e a área da secção transversal da lâmina.
(c) O efeito de Hall pode ocorrer em qualquer material condutor. Explique como se consegue determinar o sinal das cargas de condução. -
7.14.
Um ião de Mg, mono-ionizado, é acelerado por uma diferença de potencial de 2 kV e descreve uma trajetória circular no campo magnético de 50 mT de um espetrómetro de massa.
(a) Calcule o raio de curvatura da órbita do ião.
(b) Qual será a diferença entre os raios das órbitas dos iões dos isótopos Mg e Mg no mesmo campo? -
7.15.
Um feixe de partículas alfa são aceleradas, desde o repouso, no vácuo através de uma diferença de potencial de 1.6 kV e entram de seguida entre duas lâminas metálicas separadas de 7.6 mm entre si, que estão ligadas a uma f.e.m. de 200 V, tal como mostra a figura. Admitindo que o campo elétrico entre as lâminas é uniforme, qual deverão ser a direção, o sentido e o módulo do campo magnético entre as lâminas para que o feixe de partículas alfa atravesse as lâminas de forma paralela a elas e sem sofrer nenhum desvio? (Uma partícula alfa é formada por dois protões e dois neutrões, possuindo carga e massa kg.)
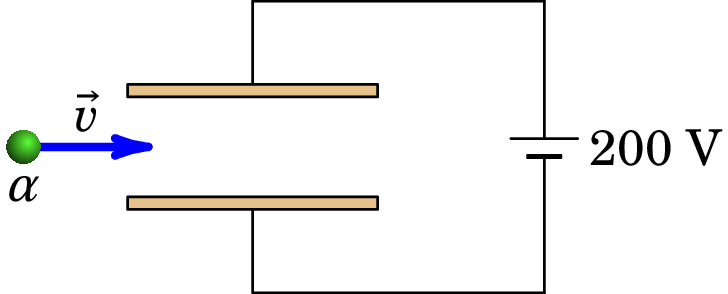
-
7.16.
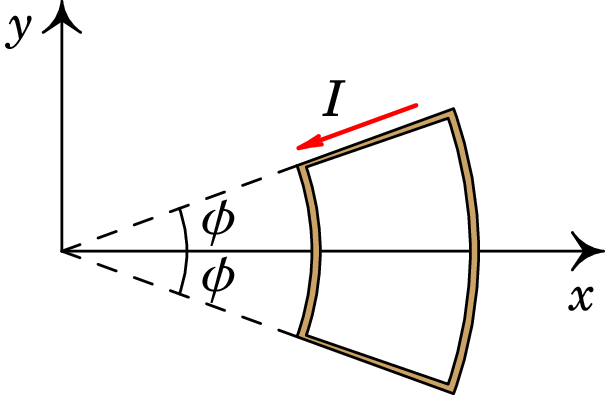
A espira da figura é formada por dois arcos de raios e (), cada um correspondente a um ângulo , e dois segmentos radiais de comprimento . Existe um campo magnético , onde é uma constante e são as coordenadas polares. Calcule o momento de binário sobre a espira quando esta é percorrida por uma corrente , no sentido indicado na figura.
Respostas
-
7.1.
(em metros).
-
7.2.
1.65 m.
-
7.3.
28.85 mm.
-
7.4.
T.
-
7.5.
(a) µN, µN,
µN. (b) .
(c) -
7.6.
(a) m/s. (b) J. (c) J.
-
7.7.
N·m
-
7.8.
, , onde , e podem ser quaisquer funções, não necessariamente constantes. As condições obtidas são as mesmas, seja a carga das partículas positiva ou negativa.
-
7.9.
81.57 mN.
-
7.11.
T + , onde é arbitrário.
-
7.12.
N·m. O momento do binário magnético é segundo , pelo que a espira roda em torno do eixo com sentido negativo de modo a alinhar o seu momento magnético na direção e sentido do campo magnético, como deve ser.
-
7.13.
(a) Como a lâmina é metálica, os portadores de carga são eletrões de condução, cuja velocidade é no sentido oposto ao da corrente , onde e é o versor da corrente. A força magnética é e aponta no sentido vertical de baixo para cima, pelo que se acumula carga negativa no lado superior da lâmina e o inferior apresenta excesso de carga positiva. (b) - . (c) No caso dos portadores de carga serem positivos com carga , a sua velocidade é no mesmo sentido da corrente elétrica , a força magnética é e aponta, tal como no caso de portadores negativos, no sentido vertical de baixo para cima; assim, passa a haver nos lados superior e inferior um excesso de carga positiva e negativa, respetivamente. A diferença de potencial de Hall possui sentido oposto ao indicado na figura. A polaridade de determina pois o sinal dos portadores de carga.
-
7.14.
(a) 63.1 cm. (b) 2.6 cm.
-
7.15.
Direção perpendicular à figura, para dentro dela, e módulo de 670.0 G.
-
7.16.
.