6. Circuitos de corrente contínua

Gustav Robert Kirchhoff (1824–1887)
Georg Simon Ohm (1789–1854) enunciou a lei que relaciona a diferença de potencial com a corrente num condutor, numa série de dois artigos publicados em 1826 e 1827. Em 1845 Gustav Kirchhoff estendeu a lei de Ohm a circuitos mais complicados, com várias fontes e resistências, na forma de duas leis para circuitos gerais. A análise dum circuito elétrico consiste em determinar a diferença de potencial e a corrente em todos os elementos do circuito. Essa análise pode ser feita usando as leis de Kirchhoff ou outros métodos, baseados nelas, que são estudados neste capítulo.
6.1 Circuitos elétricos
Neste capítulo estudam-se circuitos elétricos com resistências, condensadores e fontes de f.e.m. constantes. No caso dos circuitos com condensadores, serão considerados unicamente o instante em que os condensadores estão descarregados, atuando como curto-circuitos, ou no estado estacionário, em que a carga neles já não varia. No capítulo 10 este estudo será estendido a circuitos com resistências, condensadores, indutores e fontes de tensão alternada.
6.2 Nós, ramos e malhas
A figura 6.1 mostra um exemplo do tipo de circuito que vamos estudar, possuindo 3 fontes de f.e.m. e 7 resistências11Admite-se que as resistências no diagrama já incluem resistências internas das fontes e resistências de cabos de ligação, caso não sejam desprezáveis. As linhas entre resistências servem apenas para mostrar o diagrama de forma mais clara e não correspondem a cabos de ligação.. O nosso objetivo é determinar a voltagem (diferença de potencial) nas 7 resistências, assim como a intensidade e sentido da corrente em todos os 10 elementos. Começaremos com algumas definições que facilitam a análise do circuito.
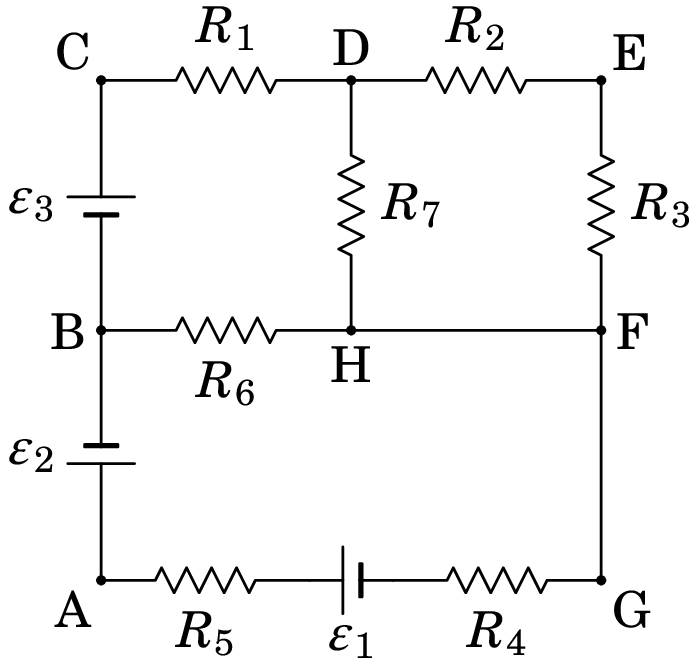
Nó: Qualquer ponto no circuito onde há divisão da corrente em dois ou mais percursos alternativos. Num nó é necessário portanto usar pelo menos 3 linhas diferentes. No circuito da figura 6.1 há quatro nós: B, D, H e F. Os pontos A, C, E e G não são nós porque nesses pontos a corrente só tem um percurso por onde circular. Cada nó pode ser caraterizado pelo valor do potencial elétrico nele.
Ramo: Percurso entre dois nós, sem nenhuma derivação. O circuito 6.1 tem 6 ramos: entre B e D (passando por C), entre D e F (passando por E), entre D e H (passando pela resistência de 3 k), entre B e H (passando pela resistência de 8 k), entre H e F (passando pelo fio sem qualquer elemento), e entre B e F (passando por A e G).
A corrente em todos os elementos de cada ramo é a mesma; i.e., cada ramo é caraterizado pelo valor da corrente elétrica que circula nele. Como tal, teremos de determinar seis correntes , , …, , correspondentes aos seis ramos.
Por exemplo, a corrente nas f.e.m. de 6 V e 9 V, e nas resistências de 6 k e 4 k terá a mesma intensidade, , e o mesmo sentido; a análise do circuito permitirá determinar se a corrente é de B para F (neste caso, a fonte de 6 V estará em modo gerador e a de 9 V em modo recetor) ou se é de F para B (estando então a fonte de 6 V em modo recetor e a de 9 V em modo gerador).
A diferença de potencial entre B e F, , obtém-se somando as diferenças de potencial nos quatro elementos nesse ramo. Como estamos a calcular o potencial de B menos o potencial de F, soma-se a diferença de potencial do extremo de cada elemento mais próximo de B menos o potencial do extremo mais próximo de F. Nas fontes, a diferença de potencial é o valor da f.e.m. , e a barra mais comprida indica o elétrodo a maior potencial, i.e., a diferença de potencial numa fonte de f.e.m. possui sempre o sentido do elétrodo positivo para o elétrodo negativo da fonte. Nas resistências, a diferença de potencial é dada pela lei de Ohm, , e o sentido que arbitrarmos para a corrente apontará no sentido do extremo da resistência com maior potencial para o extremo com menor potencial (i.e., a diferença de potencial possui o mesmo sentido que o da corrente elétrica). Assim, se arbitrarmos o sentido da corrente como sendo de B para F, a expressão da diferença de potencial nesse ramo será (em unidades SI):
| (6.1) |
É muito importante compreender esta equação que constitui uma das bases da análise de circuitos. Esta equação também mostra que a diferença de potencial entre os extremos do ramo, e a corrente nele, não dependem da ordem em que estiverem os elementos no ramo; aliás, a equação pode ser escrita da forma seguinte:
| (6.2) |
Podemos assim substituir todas as resistências no ramo por uma única resistência, igual à soma delas (equivalente em série), e as f.e.m. podem ser substituídas por uma única f.e.m. igual à soma algébrica delas, tendo em conta os seus sinais.
De referir, que no caso de termos arbitrado o sentido da corrente como sendo de F para B, então a diferença de potencial entre B e F seria escrita como: ; ou seja, muda o sinal da expressão da voltagem nas resistências mas não mudam os sinais das f.e.m. Após obtermos a solução das 6 equações dos ramos, esta indicar-nos-á qual o sentido real da corrente : caso se obtenha com sinal positivo, então o sentido arbitrado estará correto, caso contrário, o sentido real de será o oposto ao arbitrado.
Como o ramo entre H e F é um curto-circuito, o potencial desses dois nós é o mesmo; contudo, a corrente pode ter qualquer intensidade e qualquer sentido. É provável que no circuito real estes dois pontos sejam o mesmo ponto, os quais no diagrama de circuito foram indicados como dois pontos diferentes, por pura questão estética. Juntando o ponto H ao ponto F e combinando as resistências e as fontes em série nos ramos BAGF e DEF, obtém-se o circuito da figura 6.2, que é equivalente ao circuito da figura 6.1, mas tem apenas 2 fontes, 5 resistências, 3 nós e 5 ramos.
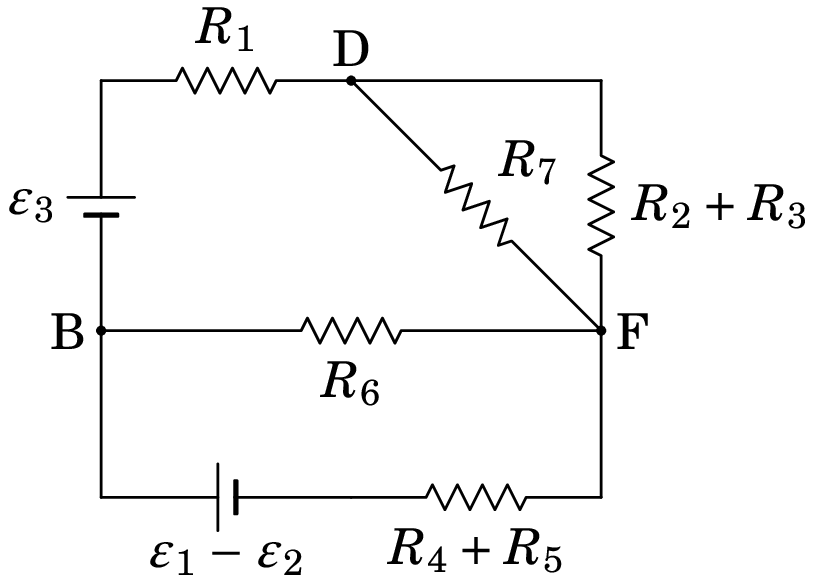
Podemos ainda substituir as resistências de 3 k e 6 k, que estão em paralelo entre os nós D e F, por uma única resistência de 2 k, entre D e F, e essa resistência soma-se à outra resistência de 2 k. Obtemos assim o circuito equivalente da figura 6.3.
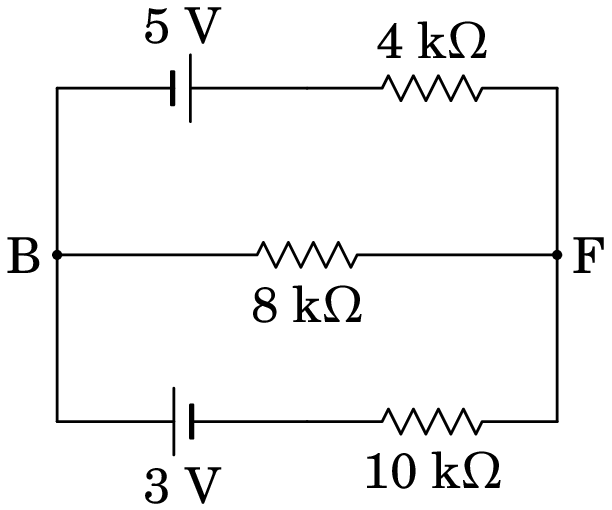
Temos agora um circuito com 2 nós e 3 ramos. As três equações dos três ramos incluem 5 variáveis: , , , e . Faltam então mais duas equações para podermos resolver o circuito, que serão introduzidas na próxima secção, mas antes de continuar definiremos ainda mais um conceito importante.
Malha: Uma malha é um qualquer percurso fechado num circuito, que não passe duas vezes pelo mesmo nó. Por exemplo, no circuito da figura 6.3 há três malhas: os dois retângulos por cima e por baixo da resistência de 8 k, e o retângulo que inclui todos os outros elementos exceto a resistência de 8 k.
Uma malha simples é uma malha em que não há nenhum nó, tal como na figura 6.4.
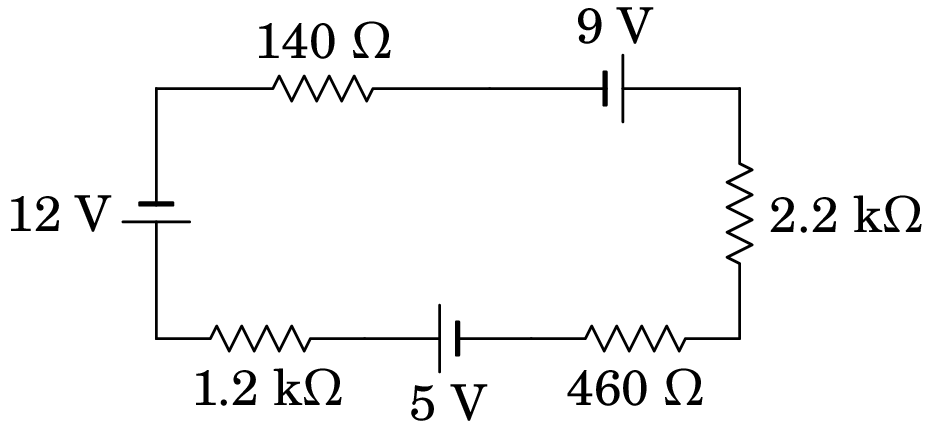
Nesse caso, a corrente deverá ser igual em todos os dispositivos na malha, e podemos aplicar a mesma equação dum ramo, em que o ponto inicial e final é o mesmo. Por analogia com a equação (6.2) do ramo entre B e F no circuito da figura 6.1, a equação da malha no circuito da figura 6.4 é, em unidades SI e arbitrando a corrente no sentido anti-horário,
| (6.3) |
ou arbitrando corrente no sentido horário. Como tal, a corrente é no sentido horário, e com intensidade:
| (6.4) |
A voltagem em cada resistência calcula-se multiplicando o valor da resistência pela corrente da malha. Na resistência de 1.2 k a voltagem é V, e as voltagens nas outras 3 resistências são V, V e V. Note que a soma das voltagens nas 4 resistências é igual à f.e.m. total, 2 V, como deve ser.
As f.e.m. de 5 V e 9 V encontram-se em modo gerador, fornecendo potências de mW e mW e a f.e.m. de 12 V encontra-se em modo recetor, absorvendo uma potência de mW. Dos 7 mW fornecidos pelos dois geradores, o recetor absorve 6 mW e o restante 1 mW é dissipado sob a forma de calor nas quatro resistências. A potência dissipada em cada resistência é igual à sua voltagem vezes a corrente que a percorre (ou, equivalentemente, igual ao valor da resistência vezes a corrente ao quadrado): as quatro resistências dissipam mW, mW, mW e mW, verificando-se assim que a potência fornecida é igual à soma da potência absorvida mais a potência dissipada, como deve ser.
6.3 Leis de Kirchhoff
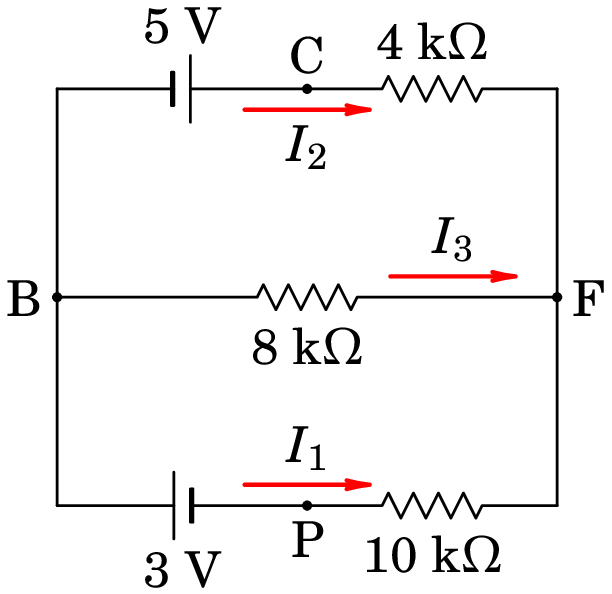
Um circuito pode ser analisado usando a lei de Ohm e duas regras simples, chamadas leis de Kirchhoff. Vamos enunciar essas leis usando o exemplo concreto do circuito da figura 6.3, que aqui reproduzimos na figura 6.5. Como já foi referido na secção anterior, esse circuito tem 2 nós e 3 malhas.
6.3.1 Lei dos nós
A lei dos nós, ou lei das correntes, estabelece que a soma algébrica das correntes em qualquer nó é igual a zero. Soma algébrica das correntes quer dizer que as correntes que convergem para o nó deverão ser somadas com sinal oposto ao das correntes que divergem do nó. Em um nó no qual divergem e convergem um número total de correntes , a lei dos nós escreve-se como:
| (6.5) |
onde às correntes que convergem é atribuído um sinal e às que divergem o sinal oposto.
Outra forma equivalente de enunciar a lei é dizer que a soma total das correntes que entram no nó deverá ser igual à soma das correntes que saem do nó. Esta lei é uma consequência do príncipio da conservação da carga elétrica, o qual se traduz na equação da continuidade anteriormente deduzida — ver equações (5.22) e (5.24). As correntes no circuito são estacionárias, e, como tal, não pode haver acumulação de carga nos nós, nem produção de carga nestes. Em qualquer intervalo de tempo, toda a carga que chega a um nó por alguma derivação tem de sair por uma outra.
No caso do circuito 6.5, há 3 correntes a serem determinadas, uma por cada ramo. Como não sabemos os seus sentidos a priori, podemos arbitrá-los e usá-los de forma consistente na lei dos nós; a resolução das equações do circuito conduzirá a sinais negativos nos casos em que o sentido real da corrente seja oposto ao que foi arbitrado. Usando as correntes , , e tal como indicado na figura 6.5, a lei dos nós em B e F conduz às seguintes equações:
| (6.6) |
As duas equações são equivalentes neste caso. Num caso geral, se existirem nós, existirão apenas equações de nó independentes.
6.3.2 Lei das malhas
A lei das malhas, ou lei das tensões 22Em circuitos, o potencial é também designado por tensão elétrica ou simplesmente por tensão. A diferença de potencial entre dois pontos é também designada por queda de tensão., diz que a soma algébrica das diferenças de potencial numa malha deverá ser igual a zero. Neste caso a soma algébrica quer dizer que percorrendo a malha, i.e, começando num dado ponto da malha e terminando no mesmo ponto, no sentido que arbitremos (direto ou retrógrado), na passagem por cada elemento deverá ser sempre somado o potencial do ponto final menos o potencial do ponto inicial em todos os elementos (ou ao contrário, em todos os elementos). Numa malha contendo elementos, em que cada elemento possui uma diferença de potencial , a lei das malhas escreve-se então como:
| (6.7) |
onde pode ser devido a uma fonte de f.e.m., a uma resistência, a um condensador, etc.
A lei das malhas é uma consequência do princípio da conservação da energia. A soma algébrica das diferenças de potencial ao longo duma malha é equivalente a calcularmos o integral de linha do campo elétrico ao longo da malha (percurso fechado), o qual, uma vez que o campo eletrostático é conservativo, conduz ao resultado nulo —ver equação (2.38).
Nas malhas com fontes, podemos explicar a conservação da energia, notando que dentro de uma fonte de f.e.m. existe um campo eletrostático que aponta do elétrodo positivo para o negativo 33De facto, dentro do eletrólito de uma bateria existe um outro campo elétrico, dito campo elétrico impresso, o qual possui sentido oposto ao do campo eletrostático e que é responsável pela passagem das cargas positivas presentes no eletrólito do elétrodo negativo para o positivo e das cargas negativas do elétrodo positivo para o negativo, mantendo assim a corrente elétrica pelo circuito exterior. Este campo impresso é não eletrostático e portanto não conservativo, estando associado às reações químicas responsáveis pelo aparecimento da força eletromotriz da fonte.. Efetuando o integral de linha do campo eletrostático ao longo da malha, usando novamente a equação (2.38), obtemos que a soma algébrica das f.e.m. das fontes na malha mais as diferenças de potencial nos elementos passivos (resistências, condensadores, etc.) da malha é igual a zero. Em termos de energia, num circuito a energia fornecida pelas fontes geradoras, a qual é proveniente da energia química destas, é igual à energia absorvida pelas fontes recetoras mais a energia dissipada nas resistências mais a energia associada a outros elementos passivos.
No exemplo da figura 6.5, as equações das 3 malhas são as seguintes:
| (6.8) |
Tendo em conta os valores das f.e.m. e a forma como estão ligadas, temos que: V e V. Usando a lei de Ohm e os sentidos das correntes arbitrados na figura 6.5, , e (todas em unidades SI). Substituindo nas equações das malhas obtemos as seguintes equações:
| (6.9) |
As primeiras duas equações são linearmente independentes, mas a terceira é a soma das duas primeiras (a terceira malha é a sobreposição das duas primeiras).
6.4 Método das malhas
No método das malhas, imagina-se o circuito como a sobreposição de malhas simples cada uma com uma corrente . No caso do circuito da figura 6.5, o circuito separa-se nas duas malhas simples apresentadas na figura 6.6, com correntes e , que podem ser arbitradas nos sentidos que mostra a figura.
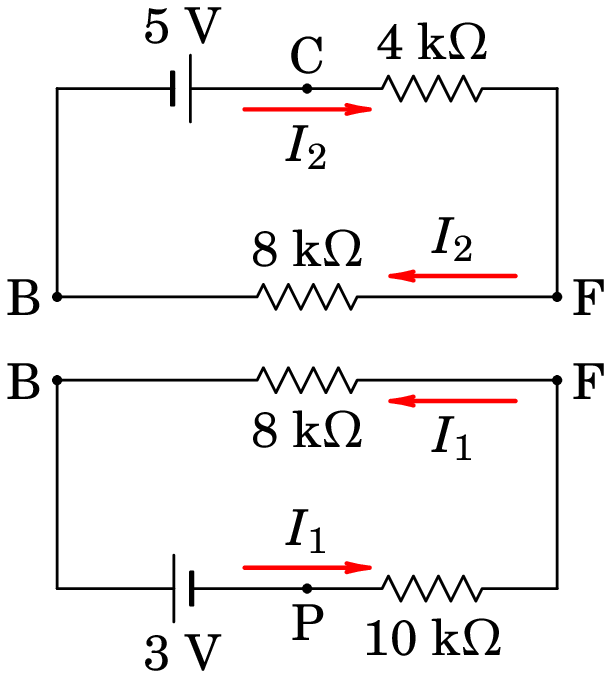
Quando colocarmos as duas malhas simples juntas, a corrente no ramo BF passa a ser , apontando de F para B. Como tal, comparando com a figura 6.5, foi substituída por 44Essa substituição faz com que a lei dos nós esteja garantida.. As duas equações das malhas são então as duas primeiras equações em (6.9), substituindo por :
| (6.10) |
Resolvem-se essas duas equações para encontrar os valores das correntes das malhas; o resultado obtido é: mA e mA. Ou seja, a corrente no ramo da f.e.m. de 3 V é 0.5 mA, de F para P, a corrente no ramo da f.e.m. de 5 V é 0.75 mA, de C para F, e a corrente no ramo do meio é 0.25 mA, de F para B.
6.5 Método dos nós
O valor do potencial nos nós de um circuito é arbitrário, pois não tem significado físico. O que tem significado físico é a diferencia de potencial entre dois nós, que determina a corrente que circula por um ramo entre esses dois nós.
O método dos nós consiste em arbitrar um valor qualquer do potencial (habitualmente zero), num nó qualquer. O valor do potencial nos restantes nós do circuito serão as variáveis do problema. Para as determinar, escreve-se a expressão da corrente em cada ramo em função dos valores do potencial nos dois nós nos extremos do ramo. A seguir, aplica-se a lei dos nós em cada nó (exceto no nó onde arbitramos o valor do potencial, pois não será necessário).
Obtém-se assim um sistema de equações lineares que permite determinar os potenciais dos nós. Substituindo esses potenciais nas expressões das correntes nos ramos, determinam-se essas correntes. Para ilustrar o método, resolveremos o circuito da figura 6.5, arbitrando potencial igual a zero no nó B, o potencial do ponto C será então V, e o potencial do ponto P será V. A única variável do sistema é então o potencial do nó F, e a única equação é a lei do nó F. A figura 6.7 mostra, em azul, os valores do potencial e, a vermelho, os sentidos arbitrados para as correntes dos ramos.
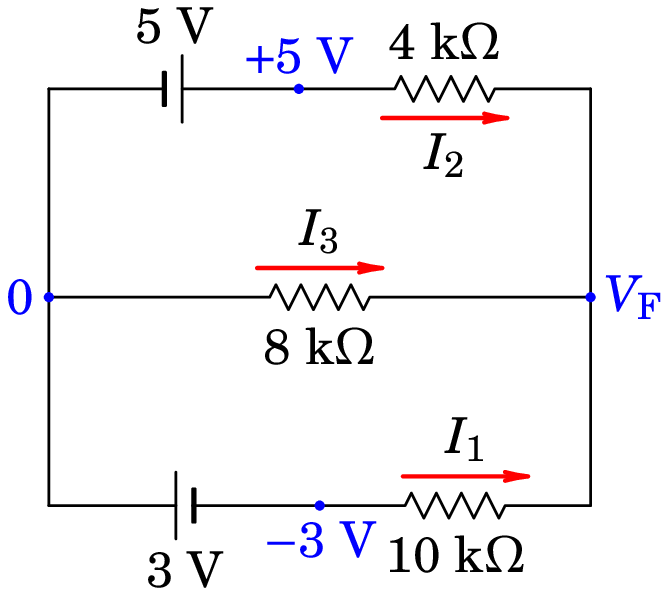
As expressões das correntes dos 3 ramos, em função de , encontram-se aplicando a lei de Ohm a cada uma das 3 resistências totais dos 3 ramos (voltagens em volt, resistências em k e correntes em mA):
| (6.11) |
E aplicando a lei dos nós em F:
| (6.12) |
Multiplicando os dois lados da equação por 40, obtém-se:
| (6.13) |
que conduz à solução V. Substituindo esse valor nas equações (6.11), conclui-se que mA, mA e mA.
Exemplo 6.1
Determine a intensidade e sentido da corrente em cada uma das 7 resistências do circuito da figura 6.1.
Resolução. Com as correntes encontradas na versão simplificada do circuito, na figura 6.7, e comparando com o circuito original da figura 6.1, vemos que a corrente , que é a corrente que passa pela f.e.m. de 5 V, de B para C, é também a corrente na resistência de 2 k:
no sentido de C para D. A corrente é a corrente que circula pelo ramo das duas f.e.m. de 6 V e 9 V, que é a mesma corrente através das resistências de 6 k e 4 k, com intensidade:
e no sentido de G para A. Na resistência de 8 k, que não foi combinada com nenhuma outra, a corrente tem a mesma intensidade de na figura 6.7:
de H para B.
Para determinar a corrente nas outras três resistências, podemos determinar primeiro a diferença de potencial entre os pontos D e F, na versão do circuito na figura 6.2. Como vimos, a resistência equivalente em paralelo entre D e F é de 2 k e, como tal,
e a partir dessa diferença de potencial obtêm-se as intensidades das correntes nas resistências de 3 k e 6 k da figura 6.2:
com sentido de D para F. Finalmente, como a resistência de 6 k foi obtida combinando as resistências de 5 k e 1 k em série, a corrente nessas resistências é a mesma (de D para F):
Observe-se que no curto-circuito entre H e F, em que a diferença de potencial é nula, circula corrente de 0.25 mA, de H para F.
6.6 Transformação delta-estrela
Três resistências ligadas entre três pontos formando um triângulo (ou um delta maiúsculo ), tal como no lado esquerdo da figura 6.8, podem ser sempre substituídas por outras três resistências ligadas a um ponto comum, tal como no lado direito da figura.
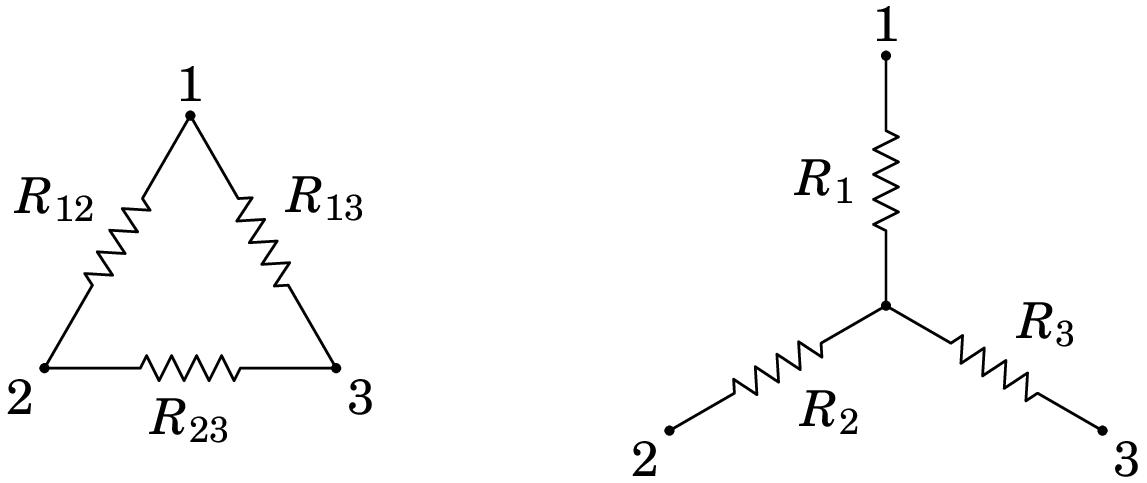
Para que as duas configurações na figura 6.8 sejam equivalentes, a condição necessária e suficiente é que a resistência entre os pontos 1 e 2, entre os pontos 2 e 3 e entre os pontos 1 e 3 seja igual nas duas configurações. Começando com os pontos 1 e 2 e na configuração estrela do lado direito da figura, como não há nada ligado no ponto 3, não passará corrente através de ; toda a corrente que passa por passa também por e a resistência entre 1 e 2 é então igual à soma destas duas resistências.
Na configuração delta do lado esquerdo da figura, a resistência entre 1 e 2 é o resultado de em paralelo com . Fazendo a mesma comparação entre os pontos 2 e 3 e os pontos 1 e 3, obtém-se o seguinte sistema de equações lineares em , e :
| (6.14) |
E a solução desse sistema linear é:
| (6.15) |
onde 1, 2 ou 3, e e são os outros dois índices, entre 1 e 3, diferentes de ( considera-se igual a ).
Exemplo 6.2
Determine a corrente fornecida pela fonte no circuito da figura seguinte:
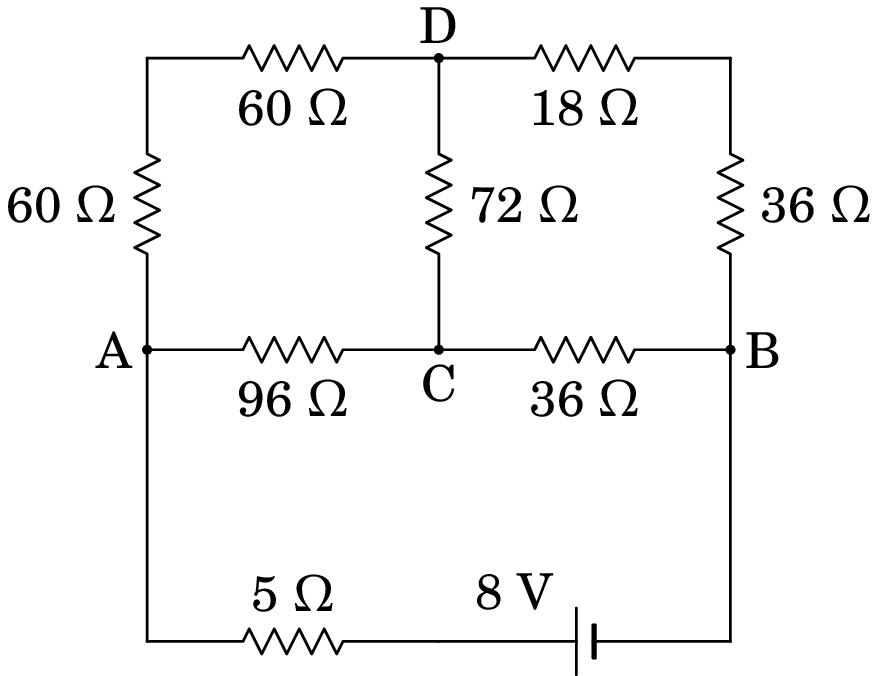
Resolução. Aplicando a transformação delta-estrela às resistências nos três ramos AD, AC e DC, obtêm-se as seguintes resistências:
Substituindo o delta ACD por uma estrela entre os pontos A, C e D, obtemos o seguinte circuito equivalente:
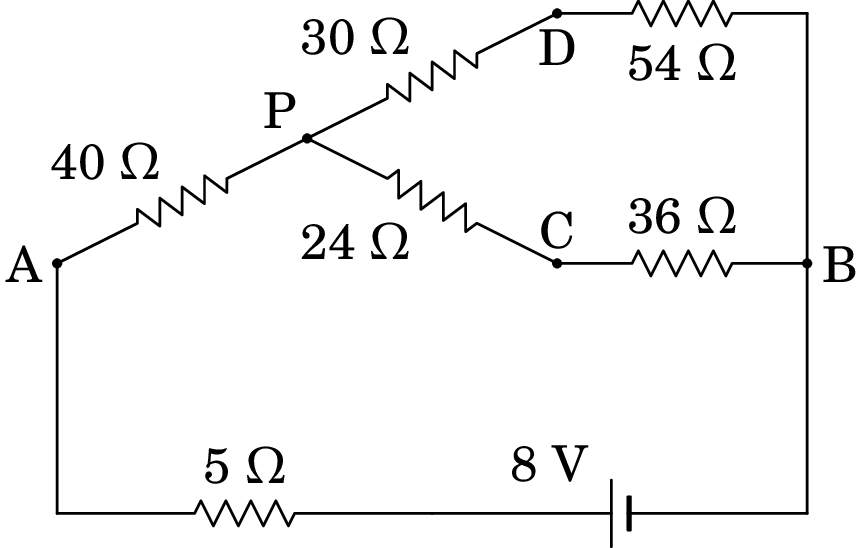
As resistências de 30 e 54 , em série, são equivalentes a 84 , e as de 24 e 36 são equivalentes a 60 . As resistências de 84 e 60 , em paralelo, são equivalentes a:
Com essa substituição obtém-se o seguinte circuito entre A e B:
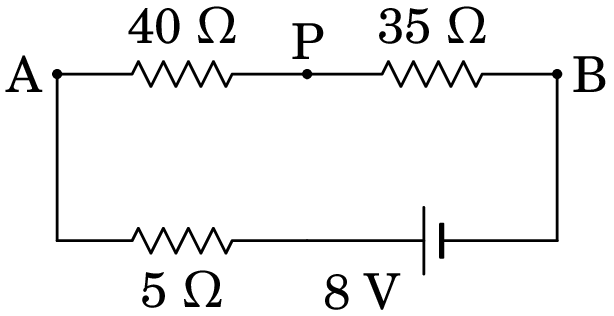
Que é uma malha simples com equação (unidades SI):
6.7 Divisão de voltagem e de corrente
Num ramo com várias resistências, , , …, , ligadas portanto em série, como na figura 6.9, a voltagem total no ramo, , distribui-se pelas várias resistências. Cada resistência terá uma diferença de potencial igual ao produto , onde é acorrente no ramo.

A corrente no ramo é , onde é a resistência total, em série; como tal, a diferença de potencial em cada resistência é:
| (6.16) |
A expressão anterior mostra que:
Num sistema de resistências em série a voltagem divide-se entre elas na proporção direta ao valor de cada resistência.
Se todas as resistências fossem iguais, cada uma teria a mesma diferença de potencial, . Se, por exemplo, uma das resistências for o dobro de outra, a sua diferença de potencial será o dobro dessa outra. No caso particular de termos apenas duas resistências e em série, a expressão (6.16) conduz ao seguinte resultado:
| (6.17) |
Consideremos agora o caso de resistências em paralelo entre dois nós A e B, tal como na figura 6.10. Admitindo que o potencial é maior no nó A, a corrente total , que entra por A distribui-se pelas resistências antes de sair por B.
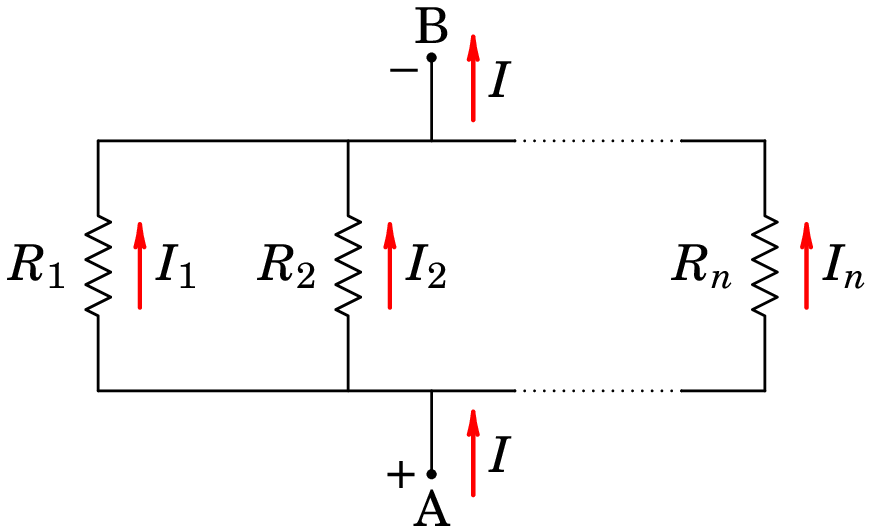
Designando por a corrente que passa pela resistência , como a diferença de potencial entre os nós A e B é , onde é a resistência equivalente das resistências em paralelo, então a corrente através de é igual a:
| (6.18) |
Dito em palavras,
Num sistema de resistências em paralelo a corrente divide-se entre elas na proporção inversa ao valor de cada resistência.
Se todas as resistências são iguais, então todas elas têm a mesma corrente . Se, por exemplo, uma das resistências for o dobro de outra, a sua corrente será metade dessa outra. No caso particular de existirem apenas duas resistências e , a expressão (6.18) conduz ao seguinte resultado:
| (6.19) |
Exemplo 6.3
Determine as correntes e as diferenças de potencial em todas as resistências do circuito do exemplo 6.2.
Resolução. Lembramos aqui a forma simplificada do circuito obtida no exemplo 6.2:
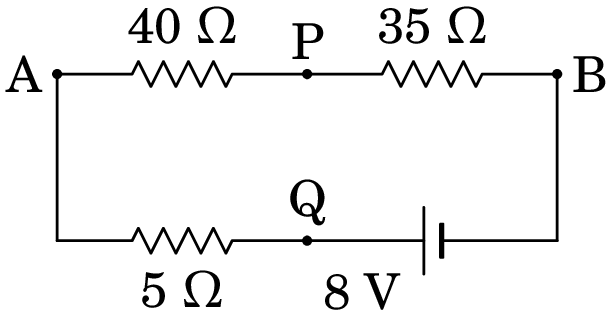
A f.e.m. da fonte distribui-se entre as 3 resistências de acordo com o princípio de divisão da voltagem (a corrente é no sentido horário):
Regressando ao circuito equivalente anterior na simplificação do circuito no exemplo 6.2,
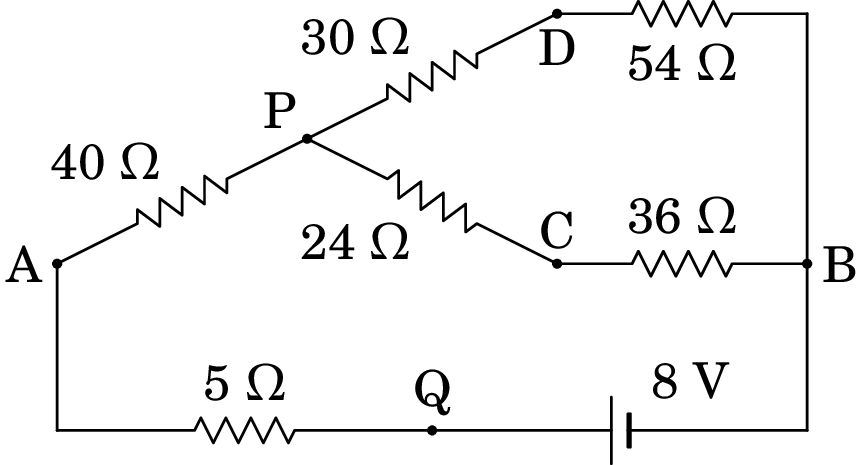
Os 3.5 V entre P e B dividem-se nos dois ramos da forma seguinte:
Consideremos agora o circuito inicial:
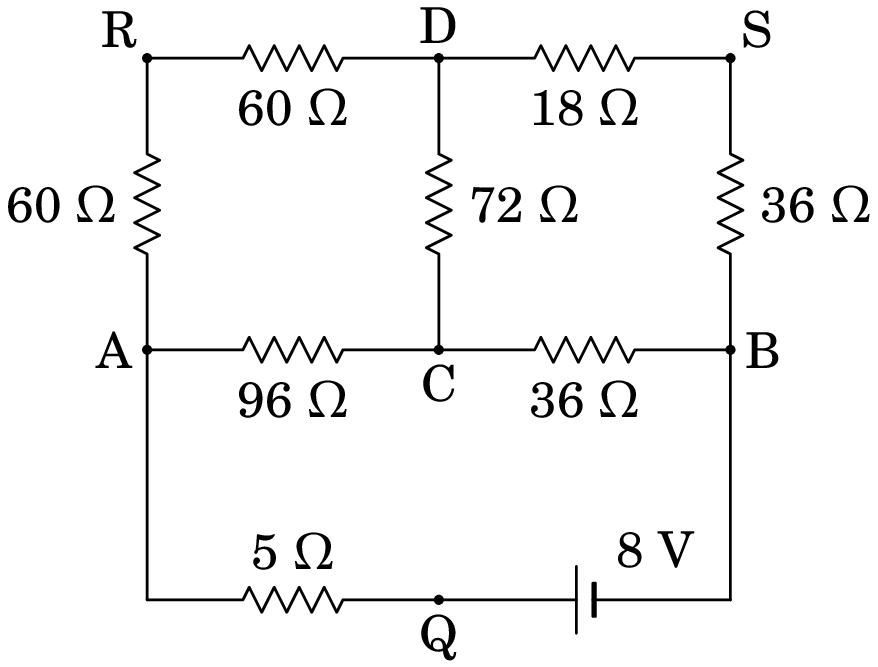
Os 2.25 V entre D e B dividem-se em:
E as voltagens nas resistências em delta entre A, C e D são:
A voltagem distribui-se por igual entre as duas resistências de 60 . A tabela seguinte mostra as voltagens nas resistências e as correntes obtidas a partir da lei de Ohm:
| Resistência | /V | /mA |
| 96 | 5.4 | 56.25 (de A para C) |
| 60 | 2.625 | 43.75 (de A para D) |
| 72 | 0.15 | 2.083 (de D para C) |
| 36 (CB) | 2.1 | 58.333 (de C para B) |
| 36 (SB) | 1.5 | 41.667 (de S para B) |
| 18 | 0.75 | 41.667 (de D para S) |
| 5 | 0.5 | 100 (de Q para A) |
O exemplo anterior podia também ser resolvido pelo método dos nós, sem usar a transformação delta-estrela, mas como o circuito tem 4 nós, teríamos de resolver um sistema de três equações com três variáveis.
6.7.1 Divisor de voltagem
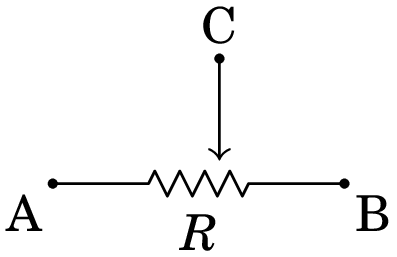
Um potenciómetro é uma resistência com um contacto móvel que pode ser deslocado desde um extremo até o outro da resistência, rodando uma barra. A figura 6.11 mostra o diagrama de circuito dum potenciómetro, com três terminais, A, B e C, em que o terminal C (no meio) é o contacto móvel. Rodando a barra, a resistência entre os terminais B e C pode ser ajustada entre 0 e .
A figura 6.12 mostra um circuito chamado divisor de voltagem. Uma fonte de f.e.m. foi ligada aos extremos de um potenciómetro de resistência .
Se for a resistência entre os terminais B e C do potenciómetro, a diferença de potencial entre esses terminais será, de acordo com princípio de divisão de voltagem,
| (6.20) |
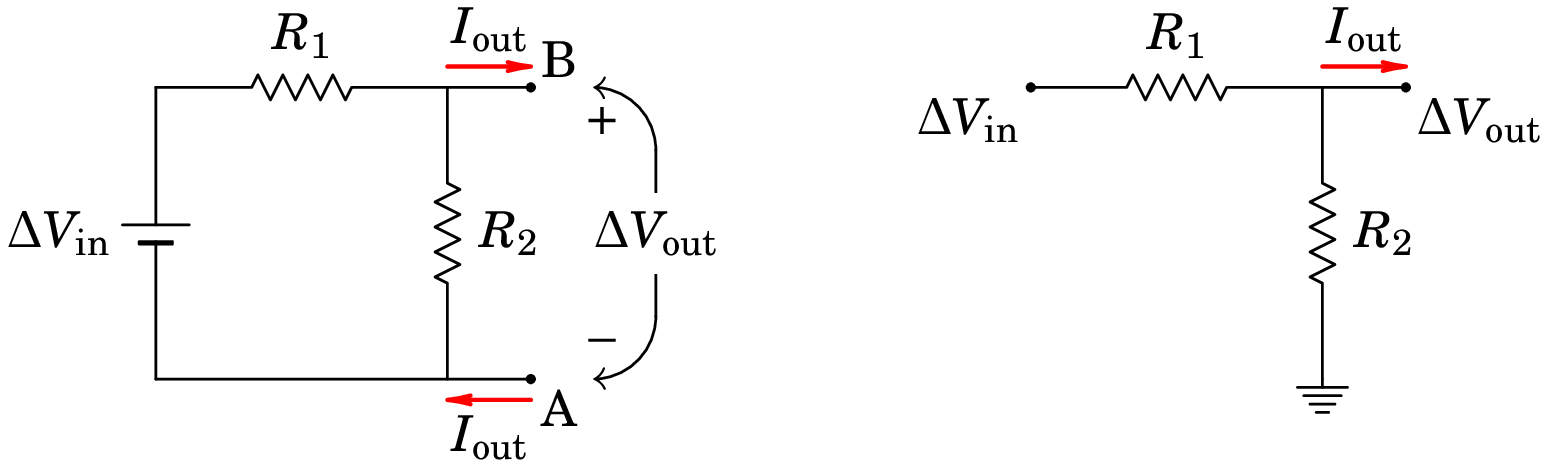
Como a resistência pode ser ajustada entre 0 e , então a voltagem pode ser ajustada entre 0 e a voltagem da fonte, , rodando a barra do potenciómetro. Ligando um dispositivo entre os terminais B e C, é possível fornecer ao dispositivo uma voltagem que pode ser ajustada entre 0 e .
6.8 Circuitos com condensadores
Quando um condensador é colocado num circuito, a diferença de potencial entre as suas armaduras é diretamente proporcional à carga armazenada no condensador, com maior potencial na armadura que tiver carga positiva. A corrente que passa pelo ramo onde estiver o condensador implica alteração da carga no condensador com a consequente alteração da sua diferença de potencial. Na armadura para onde aponta o sentido da corrente entra carga positiva, e a intensidade da corrente é igual à derivada temporal da carga armazenada.
Consideremos um condensador, inicialmente descarregado, colocado num ramo entre dois nós e , que pode incluir resistências e fontes, como na figura 6.13.
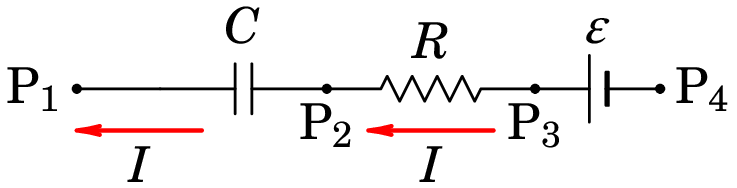
Se houver corrente no lado direito do condensador, no sentido indicado na figura, na armadura do lado direito está a entrar carga positiva; admite-se que a carga positiva na armadura do lado direito induz imediatamente carga com o mesmo valor absoluto, mas com sinal negativo, na armadura do lado esquerdo. Esse aumento da carga negativa na armadura do lado esquerdo, à mesma taxa de aumento do que na armadura do lado direito, implica corrente no lado esquerdo do condensador com a mesma intensidade e sentido do que no lado direito.
Se a corrente for no sentido indicado na figura 6.13, é porque o potencial de é maior do que o potencial de . No instante inicial, no condensador, porque está descarregado, mas é diferente de zero, porque a corrente é diferente de zero. Nesse instante, o condensador é equivalente a um curto-circuito (ou interruptor fechado), em que a diferença de potencial é nula, mas pode circular qualquer corrente.
Quando o condensador está descarregado, e a voltagem na resistência é . À medida que a carga no condensador aumenta, a voltagem na resistência, , diminui, e chegará um momento em que essa voltagem e a corrente serão nulas; a partir desse instante, a carga no condensador e o potencial do ponto permanecerão constantes.
Se a carga no condensador permanece constante, diz-se que está no estado estacionário. Nesse estado, em que não deixa passar corrente, mas mantém uma diferença de potencial entre as armaduras, o condensador é equivalente a um circuito aberto (ou interruptor aberto).
O estado intermédio, em que há corrente e carga diferentes de zero no condensador, chama-se estado transitório. Determinar a variação temporal das voltagens e correntes do circuito no estado transitório corresponde a resolver equações diferenciais, que está para além dos objetivos deste livro; contudo, nas secções 6.8.1, 9.4.1 e 10.1 mostraremos como determinar a tensão e a corrente no estado transitório em circuitos RC, RL e LC. Nesta secção consideram-se apenas condensadores descarregados ou no estado estacionário.
Exemplo 6.4
Um condensador de 1.2 µF, inicialmente descarregado, liga-se a uma pilha com f.e.m. de 9 V e resistência interna de 230 e usa-se um voltímetro com resistência interna de 3.2 k para medir a voltagem no condensador. (a) Determine a corrente na pilha, no instante inicial e no estado estacionário. (b) Determine o valor da carga do condensador no estado estacionário.
Resolução. A ligação do condensador à pilha pode ser representada por um interruptor inicialmente aberto, tal como no diagtrama seguinte. O voltímetro, representado pela sua resistência interna de 3.2 k, é ligado em paralelo com o condensador.
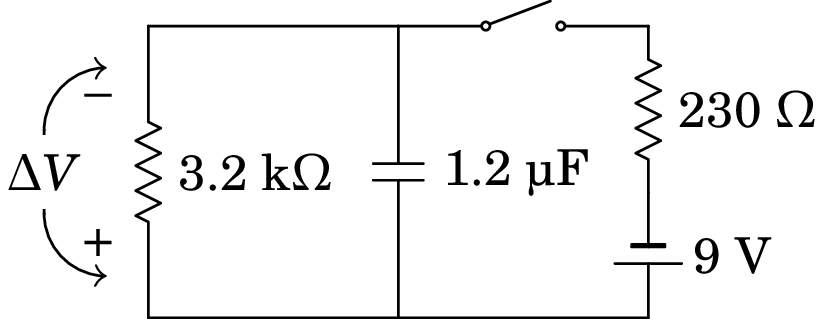
(a) No instante inicial, quando se fecha o interruptor, o condensador está descarregado, e o circuito equivalente é o seguinte:
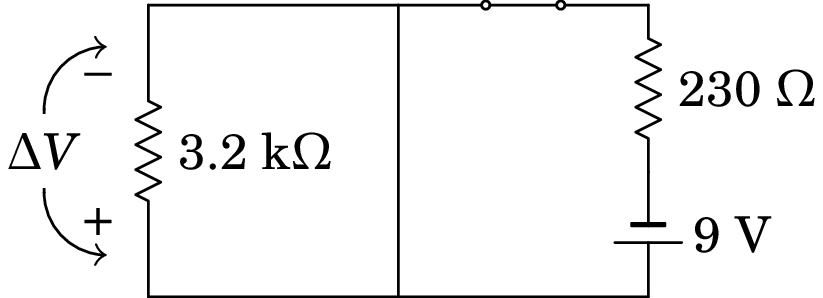
A voltagem no voltímetro é nula no instante inicial por ser igual à voltagem do condensador; como tal, a corrente inicial no voltímetro também é nula. Na pilha, a corrente inicial é:
No estado estacionário, quando a carga do condensador já não aumenta, este é equivalente a um interruptor aberto e o circuito equivalente é o seguinte:
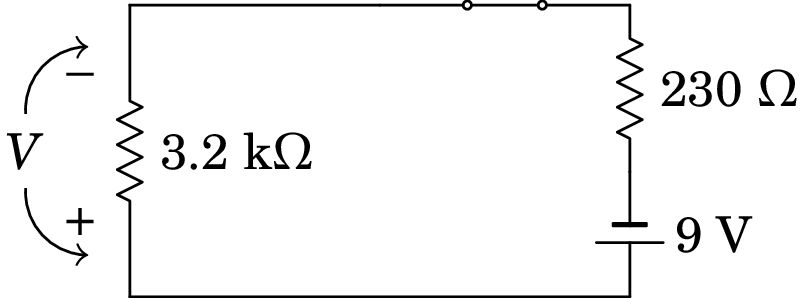
A corrente nesse caso é,
(b) Como o condensador está ligado em paralelo com o voltímetro, a diferença de potencial final entre as suas armaduras é igual à diferença de potencial final na resistência de 3.2 , que é:
e a carga final do condensador é,
Nos circuitos com várias fontes e vários condensadores, substituindo os condensadores por curto-circuitos, no estado inicial, e por circuitos abertos, no estado estacionário, obtêm-se dois circuitos diferentes, que podem ser analisados pelo método dos nós para determinar as correntes e voltagens, no estado inicial e no estado estacionário.
Exemplo 6.5
No circuito representado no diagrama, determine a potência dissipada em cada resistência e a energia armazenada em cada condensador, no estado estacionário.
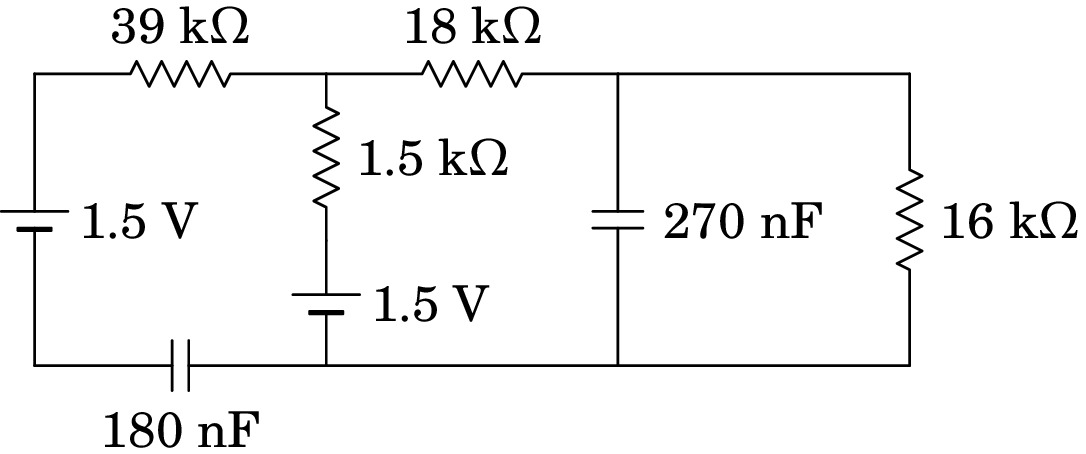
Resolução. Quando o circuito estiver no estado estacionário, os condensadores são equivalentes a circuitos abertos e o diagrama do circuito equivalente é o seguinte:
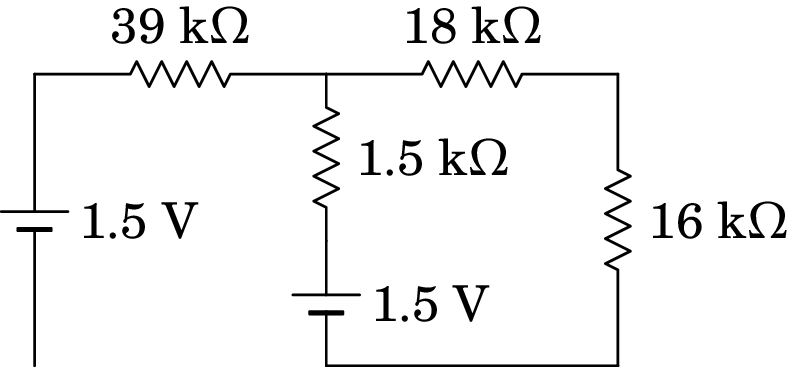
Na resistência de 39 k a corrente é nula (não tem por onde circular) e o circuito tem apenas uma malha, com resistência total 1.5 + 18 + 16 = 35.5 k e corrente igual a,
A partir dessa corrente calculam-se a seguir todas as potências dissipadas nas resistências e as energias armazenadas nos condensadores.
Na resistência de 39 k, , já que a corrente é nula.
Na resistência de 18 k,
Na resistência de 16 k,
Na resistência de 1.5 k,
No condensador de 270 nF, a diferença de potencial é a mesma que na resistência de 16 k:
e a energia armazenada nesse condensador é
No condensador de 180 nF, um possível percurso entre os dois pontos onde está ligado passa pela fonte do lado esquerdo, pela resistência de 39 k (com diferença de potencial nula), pela resistência de 1.5 k e pela segunda fonte. Como tal,
Quando um condensador, inicialmente descarregado, é ligado a uma fonte com f.e.m. e resistência interna , a voltagem entre as armaduras do condensador é a voltagem da fonte no modo gerador:
| (6.21) |
como no instante inicial no condensador é nula, a corrente inicial que passa pelo condensador é,
| (6.22) |
ou seja, igual à corrente máxima que pode fornecer a fonte. Quando o condensador atinge o estado estacionário, a corrente é nula, a voltagem no condensador fica igual a , e a carga final no condensador é:
| (6.23) |
Como tal, um condensador pode usar-se para determinar a f.e.m. e a resistência interna de uma fonte. A f.e.m. da fonte, , é igual à voltagem do condensador, no estado estacionário, e a sua resistência interna, , é igual à voltagem no estado estacionário dividida pela corrente inicial.
Exemplo 6.6
No circuito representado na figura, o condensador está inicialmente descarregado. Determine a corrente inicial no condensador e a carga no estado estacionário, indicando a sua polaridade.
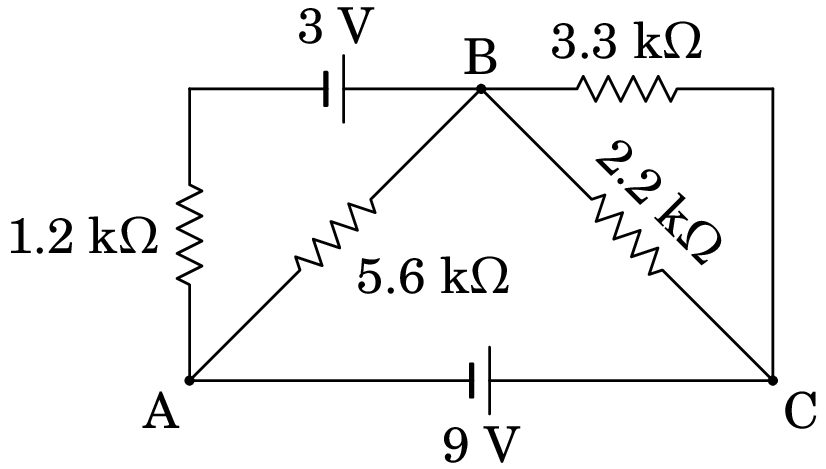
Resolução. No instante inicial, o condensador pode ser considerado um interruptor fechado. A figura seguinte mostra o diagrama do circuito equivalente, após ter combinado as resistências de 2.2 k e 3.3 k que estão em paralelo, e ter mudado a forma geométrica do circuito (apenas por questão de gosto pessoal):
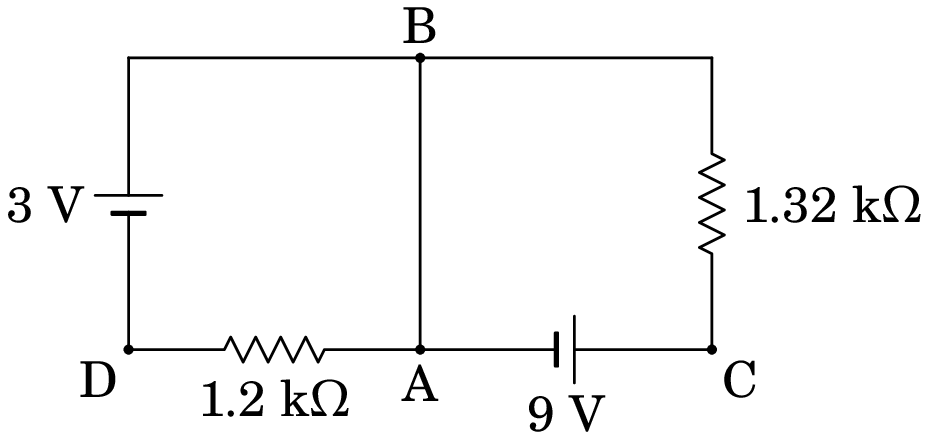
O potencial nos pontos A e B é o mesmo, e podemos arbitrar que é igual a zero. Como tal, o potencial no ponto C é 9 V, e no ponto D é V. As correntes nas duas resistências são:
No nó A sai corrente para o ponto D, e sai corrente para o ponto C. Isso implica que a corrente inicial no condensador (corrente entre A e B) é de mA, de B para A.
No estado estacionário, o condensador é equivalente a um interruptor aberto. Como tal, não existe ligação entre os pontos A e B, e o diagrama equivalente do circuito é o seguinte:
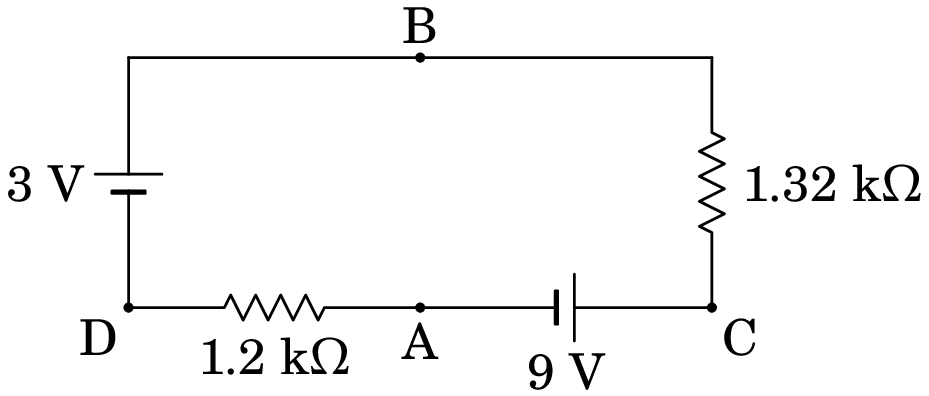
A corrente nessa malha simples é,
e circula em sentido anti-horário. A diferença de potencial na resistência de k é,
e a diferença de potencial entre A e B é,
Finalmente, a carga armazenada no condensador, no estado estacionário, é:
O resultado do exemplo anterior mostra que as duas f.e.m. e três resistências ligadas entre os pontos A e B podiam ser substituídas por uma única fonte com f.e.m. de 5.857 V (voltagem do condensador no estado estacionário), e resistência interna de 628.4 (f.e.m. dividida pela corrente inicial no condensador).
6.8.1 Circuito RC
Mostraremos aqui como determinar o estado estacionário de um circuito RC, formado por uma resistência em série com um condensador de capacidade . A corrente e a diferença de potencial (ou tensão) no condensador serão funções do tempo, que designaremos por e (sem escrever o delta em , para simplificar a notação).
Na figura 6.14 o circuito RC está ligado a uma fonte ideal de f.e.m. usada para fornecer carga inicial no condensador. Num instante designado por abre-se o interruptor S para desligar a fonte e o diagrama do circuito passa a ser o que está representado no lado direito da figura. Admitindo que a fonte esteve ligada o tempo suficiente para que o condensador atingisse o seu estado estacionário, a tensão inicial no condensador, em , é igual ao valor da f.e.m., , sendo portanto a sua carga inicial igual a (conforme a expressão (4.57)).
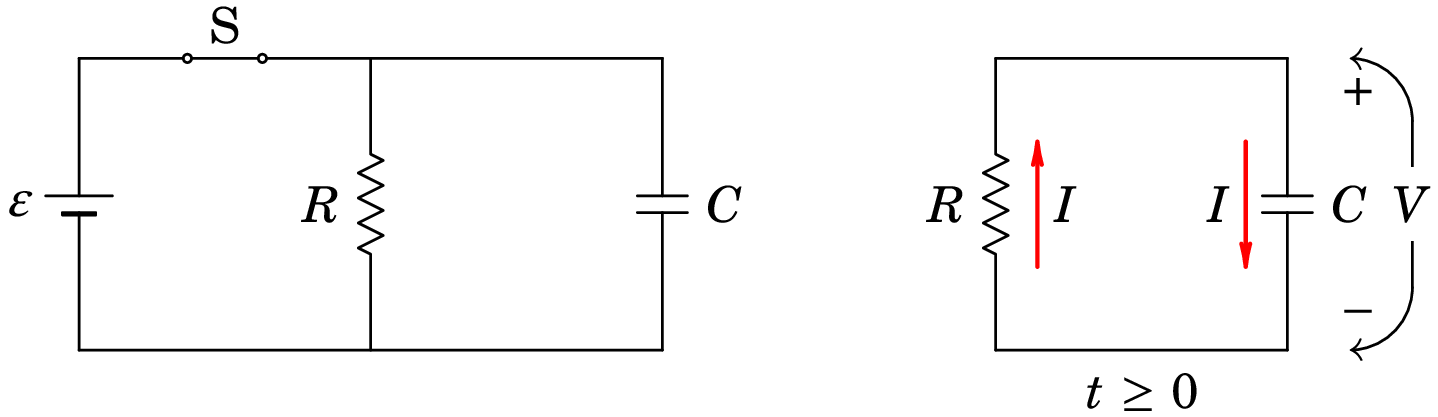
Como mostra a expressão (4.57) do capítulo 4, a carga armazenada no condensador é diretamente proporcional à tensão no condensador, sendo portanto também função do tempo:
| (6.24) |
Definem-se os sentidos positivos da tensão e a corrente no condensador de forma consistente com a definição na lei de Ohm para uma resistência, como indicado na figura 6.14. Como tal, um valor positivo de indica aumento da carga positiva no condensador e a derivada temporal de é a função . Derivando a equação (6.24), obtém-se a relação entre a corrente e a tensão no condensador:
| (6.25) |
Na resistência, a corrente e a tensão são as mesmas do que no condensador, mas o sentido positivo escolhido para corrente é oposto ao sentido positivo da tensão (corrente a passar de menor para maior potencial). Como tal, a lei de Ohm na resistência é,
| (6.26) |
e igualando à equação (6.25) obtém-se a seguinte equação diferencial:
| (6.27) |
A equação (6.27) diz que a tensão é uma função que quando derivada em ordem a , o resultado é a mesma função multiplicada pela constante . Como tal, será uma função exponencial com expoente , multiplicada por uma constante; constante esta que deverá ter o valor de no instante :
| (6.28) |
A constante chama-se constante de tempo do circuito, porque tem unidades de tempo. Em unidades SI, o produto de um ohm vezes um farad é um segundo:
| (6.29) |
A carga em função do tempo obtém-se a partir da expressão (6.24),
| (6.30) |
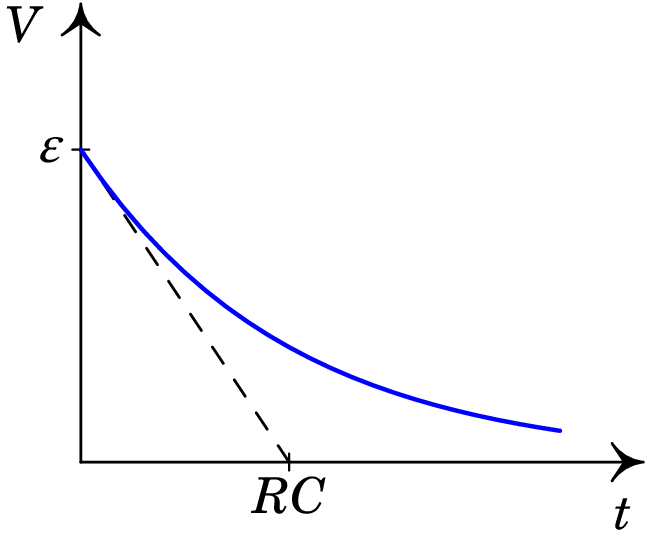
A figura 6.15 mostra os gráficos da tensão e da carga no condensador, expressões (6.28) e (6.30), em função do tempo. As retas a tracejado são as tangentes às curvas em . Os seus declives são iguais às derivadas das funções e em . Usando a expressão (6.27), os declives são dados por e , respetivamente, e as equações das retas são então:
| (6.31) |
as quais cortam o eixo do tempo em .
 |
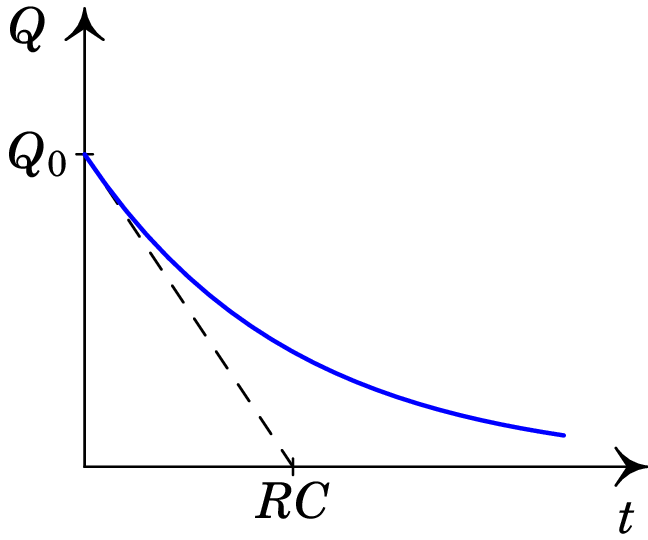 |
A tensão e carga armazenada no condensador diminuem exponencialmente, desde os seus valores iniciais e até zero. Se estas continuassem a diminuir à mesma taxa inicial (i.e., linearmente), demoraria um tempo igual à constante de tempo para serem iguais a zero. Quanto maior for a constante de tempo, mais lenta será a diminuição exponencial da tensão e da carga no condensador, até estas serem nulas, i.e., até ao condensador ficar descarregado.
A corrente calcula-se a partir da tensão usando a equação (6.26)
| (6.32) |
que é uma função exponencial que aumenta desde a corrente inicial até zero. O valor negativo da corrente indica que o condensador atua como dispositivo ativo e não passivo, como foi admitido na escolha dos sentidos positivos de e de na figura 6.14.
Problemas
-
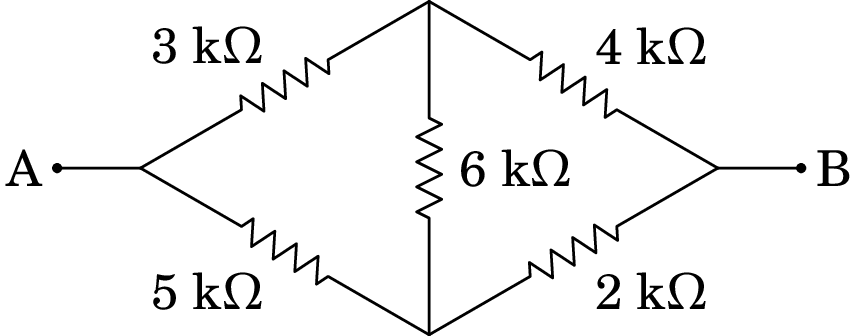
6.1.
Determine a resistência equivalente entre os pontos A e B.
-
6.2.
Considere duas resistências e ligadas em paralelo. Uma corrente total distribui-se entre as duas resistências, passando corrente por e corrente por . Admita que as correntes e podem tomar qualquer valor (inclusivamente negativo) desde que . Determine os valores de e que minimizam a potência dissipada por efeito Joule nas resistências e mostre que se obtém o resultado da equação (6.19).
-
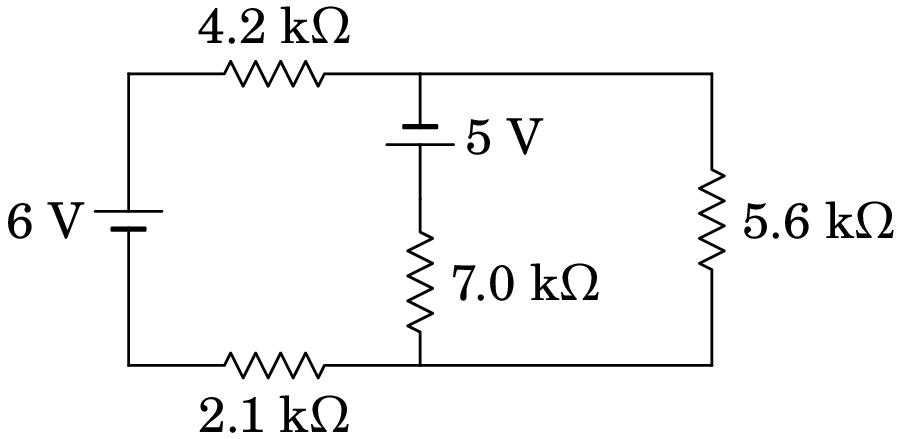
6.3.
No circuito da figura, determine quais das fontes de força eletromotriz fornecem ou absorvem energia e calcule a potência fornecida, ou absorvida, por cada uma.
-
6.4.
Uma resistência de 2.7 k liga-se a duas pilhas, em paralelo, ambas com a mesma f.e.m. de 9 V, mas com diferentes resistências internas, tal como mostra o digrama seguinte.
(a) Determine a corrente na resistência de 2.7 k.
(b) Qual das duas pilhas fornece maior potência?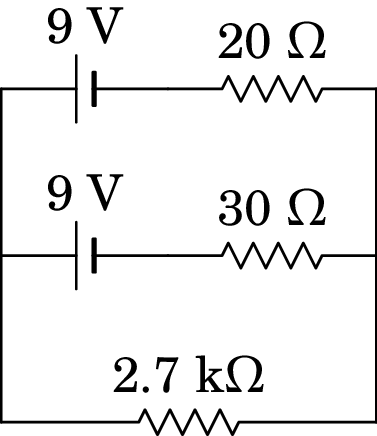
-
6.5.
Uma fonte com voltagem é ligada a uma resistência , mas pretende-se que a voltagem nessa resistência seja reduzida para , menor do que a voltagem de entrada . Para conseguir esse objetivo, usa-se um circuito chamado atenuador. A figura mostra, dentro da caixa a tracejado, um possível circuito atenuador que tem a vantagem de permitir fazer com que a resistência entre os pontos de entrada A e B continue igual à resistência do dispositivo ligado entre os pontos de saída C e D.
(a) Mostre que para que a resistência entre A e B seja igual a , as resistências e do atenuador devem verificar a condição:(b) Se e verificam a condição da alínea anterior, mostre que o fator de atenuação, é dado pela expressão:
(c) Determine os valores de e que fazem com que a resistência entre A e B seja igual a , com atenuação .
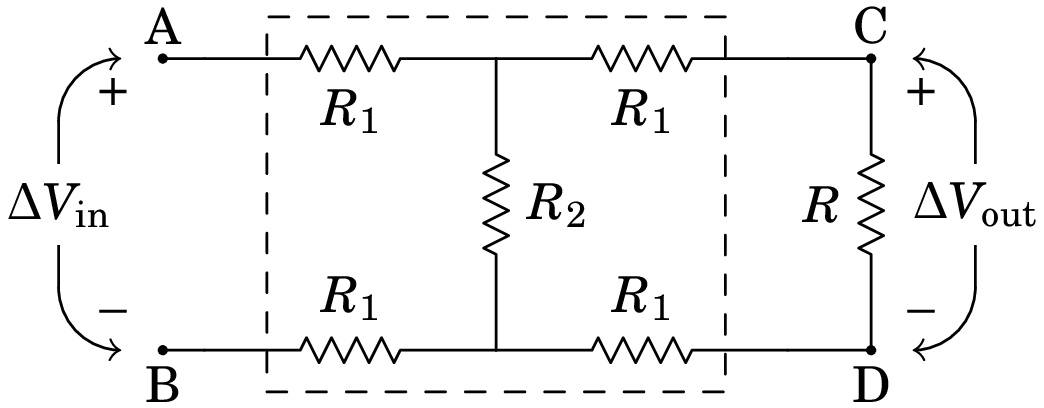
(Problema retirado de Nilsson e Riedel 2015, pág. 117)
-
6.6.
Determine a potência dissipada em cada resistência no circuito representado no diagrama e a potência fornecida pela f.e.m. Verifique que a potência fornecida pela f.e.m. é igual à soma das potências dissipadas em todas as resistências.
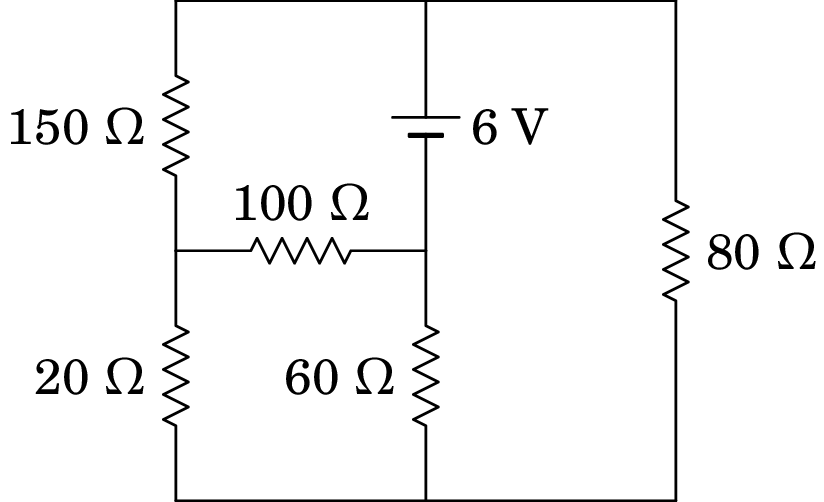
-
6.7.
No circuito representado no diagrama, os dois condensadores estão inicialmente descarregados. Determine:
(a) As correntes iniciais nas resistências e condensadores.
(b) As cargas finais nos condensadores, indicando as suas polaridades.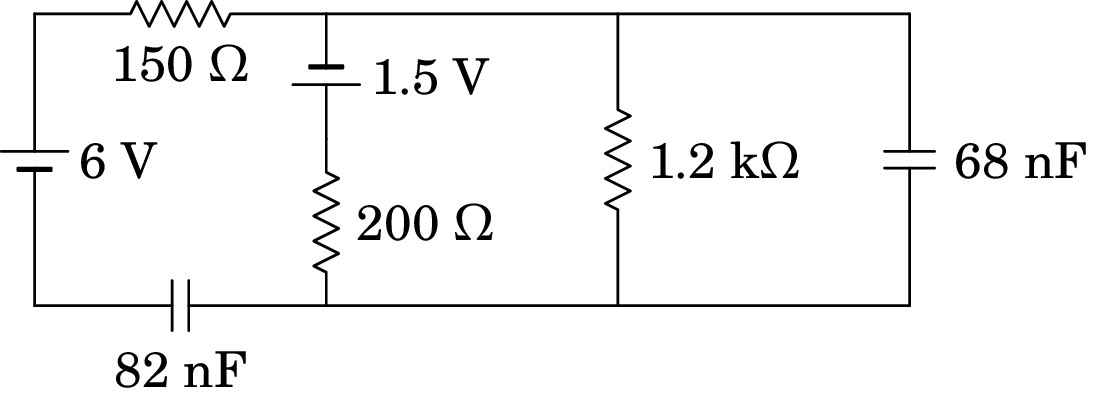
-
6.8.
Relativamente ao circuito da figura abaixo:
(a) Determine a intensidade e sentido da corrente no instante inicial no condensador, sabendo que este estava inicialmente descarregado.
(b) Determine a carga final no condensador, indicando a sua polaridade.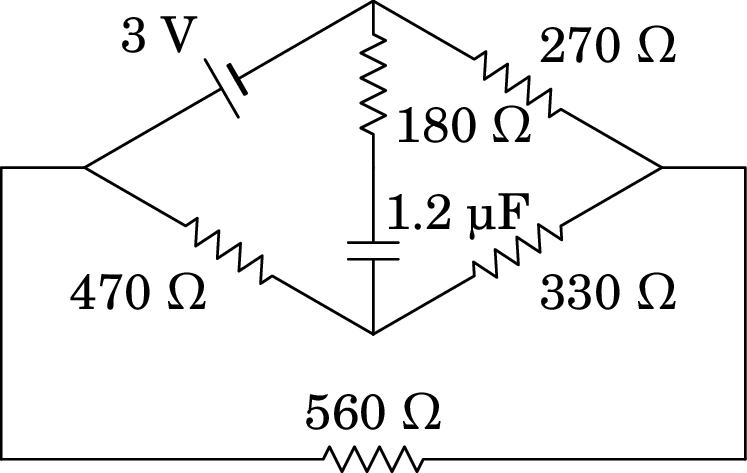
-
6.9.
No problema 6.6.6, se a resistência de 100 for substituída por um condensador de 39 nF, qual a energia final armazenada nesse condensador?
-
6.10.
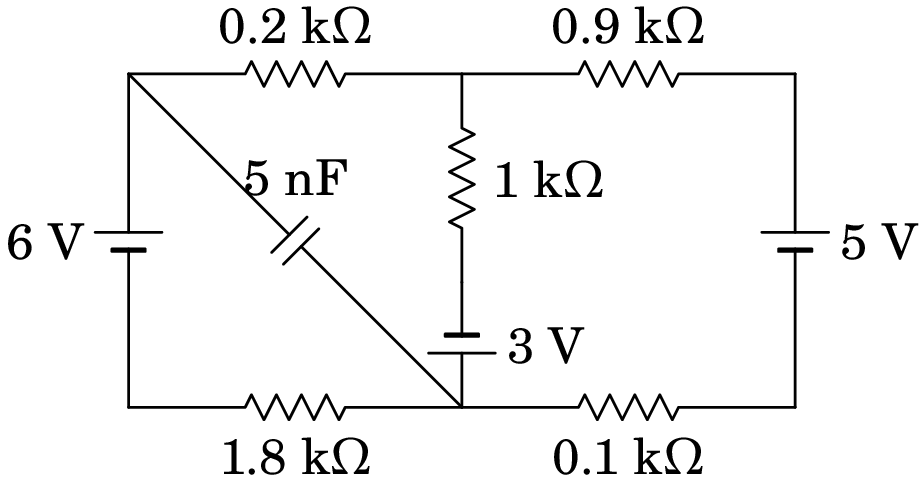
No circuito representado no diagrama, determine a carga no condensador, no estado estacionário ().
-
6.11.
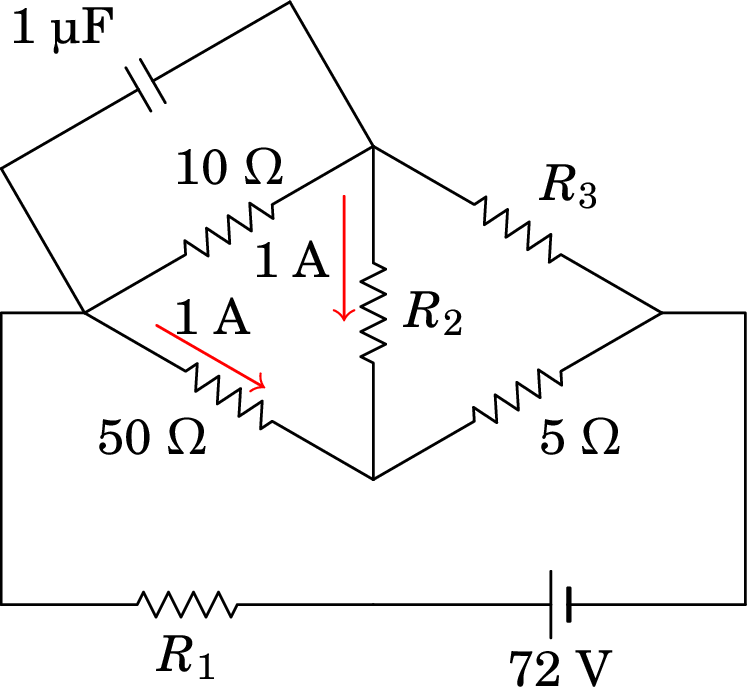
No circuito representado no diagrama, sabendo que no estado estacionário (após muito tempo) a carga no condensador é igual a 40 µC e as correntes na resistência de 50 e em são ambas 1 A, no sentido indicado, determine os valores de , e .
-
6.12.
No circuito representado no diagrama:
(a) Determine a corrente e diferença de potencial na resistência de 6 k.
(b) Determine as correntes nas resistências de 10 k e 15 k.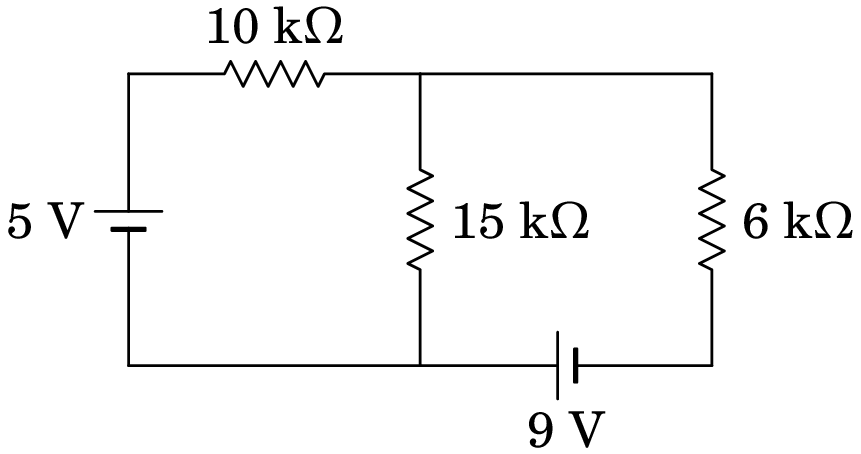
Respostas
-
6.1.
3.3939…k.
-
6.2.
Há duas variáveis, e . A potência total, em função de é ou, em função de , . Derivando essas duas expressões em ordem a e e igualando a zero, obtém-se e
-
6.3.
As duas fontes fornecem potência; a f.e.m. de 6 V fornece 5.24 mW, e a f.e.m. de 5 V fornece 3.93 mW.
-
6.4.
(a) 3.32 mA. (b) A que tem resistência interna menor (20 ).
-
6.5.
(a) A resistência entre A e B é igual a duas resistências em série com o sistema de em paralelo com em série com as outras duas resistências . (b) Para determinar , encontra-se a voltagem no sistema de em paralelo com em série com as duas resistências , usando divisão de voltagem, e usa-se novamente divisão de voltagem para determinar a voltagem em . (c) , .
-
6.6.
Na resistência de 20 , 45 µW. Na resistência de 100 , 62.0 mW. Na resistência de 150 , 82.1 mW. Na resistência de 60 , 105.8 mW. Na resistência de 80 , 151.4 mW. A f.e.m. fornece 401.4 mW.
-
6.7.
Usando subíndices iguais ao valor da resistência ou capacidade, (a) , mA, mA, mA. (b) , mA, nC (positiva na armadura de baixo e negativa na de cima), nC (positiva na armadura da direita e negativa na da esquerda).
-
6.8.
(a) 4.78 mA, de baixo para cima. (b) 2.44 µC (negativa na armadura de cima e positiva na de baixo).
-
6.9.
236.5 nJ.
-
6.10.
12 nC.
-
6.11.
, , .
-
6.12.
(a) 1 mA e 6 V. (b) Na resistência de 10 k, 0.8 mA, e na resistência de 15 k, 0.2 mA.