1. Ótica geométrica

1.1. Raios luminosos

Um ponto luminoso emite luz que se propaga em linha reta nas direções radiais com centro nesse ponto. Cada uma dessas linhas retas é o que designamos por raio de luz. Trata-se de uma ferramenta matemática, mais do que um conceito físico, que já tinha sido proposta por Euclides no seu livro "Ótica" (c. 300 a.C.). Num meio isótropo (igual em todas as direções) e homogéneo (igual em todos os pontos), os raios luminosos são linhas retas uma vez que não se podem curvar em nenhuma direção preferencial.

Uma primeira evidência da propagação da luz em linha reta são as sombras bem definidas produzidas pelos objetos iluminados por uma fonte luminosa. A região escura na sombra do objeto são os pontos em que a reta desde o ponto até a fonte interseta o objeto; como tal, nenhum dos raios que saem da fonte consegue atingir esses pontos na sombra.

Outra evidência da propagação da luz em linha reta é a câmara escura, que consiste numa caixa escura com um pequeno orifício numa das suas paredes; a luz que passa pelo orifício produz uma imagem dos objetos fora da caixa, na parede oposta da caixa. A figura 1.1 mostra a imagem da paisagem de Lisboa, produzida na câmara escura do Castelo de São Jorge. Cada ponto luminoso na paisagem produz um ponto na imagem, na posição que está na reta que passa pelo ponto luminoso e pelo orifício. Na câmara do Castelo de São Jorge o orifício encontra-se no teto de um quarto escuro, e fora da cobertura há um sistema de espelhos (periscópio) que permite desviar os raios de luz horizontais na direção vertical passando pelo orifício e produzindo a imagem no chão. A propagação dos raios de luz em linha reta conduz a imagens muito realistas na câmara escura, que já têm sido aproveitadas pelos pintores desde há vários séculos.

Os raios luminosos, que saem de um ponto luminoso nas direções radiais, podem ser desviados produzindo um feixe com raios paralelos, tal como na figura 1.2. Coloca-se uma lente convergente frente da fonte, a uma distância apropriada, que faz com que o feixe de luz cónico que sai da fonte e atinge a lente seja desviado formando um feixe cilíndrico. O tamanho do feixe pode ser reduzido colocando uma barreira com um pequeno orifício circular; o feixe paralelo é composto por raios de luz paralelos.

A velocidade da luz tem sido medida com precisão, e o seu valor, no vácuo é,

No entanto, neste livro usaremos apenas 4 algarismos significativos, aproximando o valor para $c=2.998\times {10}^8$ m/s.

1.2. Reflexão da luz

Alguns objetos, como o ecrã do televisor na figura 1.3, emitem raios de luz que se propagam em linha reta em várias direções. Cada ponto luminoso no ecrã emite raios nas direções radiais da esfera com centro no ponto.

Os raios de luz provenientes de uma fonte luminosa são refletidos pelos objetos à sua volta. Em alguns objetos a luz que incide em cada ponto da sua superfície diverge propagando-se nas direções radiais da esfera com centro nesse ponto, de forma semelhante à luz que sai de um ponto luminoso. Esse tipo de reflexão é designada de difusa.

Na figura 1.3 todos os objetos diferentes do ecrã do televisor produzem reflexão difusa; a luz do Sol após ser refletida por outros corpos no exterior do quarto, entra pela janela sendo refletida pelos objetos no quarto. Cada objeto absorve algumas partes da luz incidente e reflete outras partes, dando origem às diferentes cores dos diferentes objetos; há ainda outros objetos, como as folhas da árvore na figura 1.3, que para além de refletir a luz verde, deixam passar também parte dessa luz através deles (objetos translúcidos).

Quando a superfície do objeto que reflete a luz é completamente lisa, a reflexão designa-se de especular. O ângulo ${\theta }_{\mathrm{i}}$ (ângulo de incidência) que cada raio de luz faz com a perpendicular à superfície, no ponto onde é refletido, é igual ao ângulo ${\theta }_{\mathrm{r}}$ (ângulo de reflexão) que o raio faz com a mesma perpendicular após ser refletido (ver figura 1.4):

Na figura 1.3, alguns há alguns objetos lisos a produzirem reflexão especular: a secção mais luminosa no chão é a reflexão especular da luz do céu e a barra de som por baixo do ecrã do televisor produz reflexão especular da luz do ecrã. Esses dois objetos que produzem reflexão especular produzem também reflexão difusa. Essa dupla reflexão pode ser compreendida mais facilmente no caso da capa plastificada do livro da figura 1.5. A película plástica que cobre a capa é lisa e produz a reflexão especular observada na parte de baixo. Mas o plástico transparente também deixa passar parte da luz para a superfície pintada sobre o cartão da capa, onde é produzida a reflexão difusa que observamos no resto da capa.

A figura 1.6 mostra uma superfície áspera coberta por uma película transparente e lisa. Uma parte de cada raio que atinge a superfície lisa da película é refletido, e a parte restante penetra a película transparente sendo depois refletido na superfície áspera por baixo da película transparente.

A luz refletida na superfície plana é mais intensa, mas cada raio refletido ilumina uma zona específica; já a luz da reflexão difusa na superfície áspera é mais fraca mas dispersa-se em várias direções, iluminando toda região por cima da superfície.

1.3. Refração da luz

Num meio diferente do vácuo, a luz propaga-se com velocidade menor do que a sua velocidade $c$ no vácuo. Define-se o índice de refração de um material:

onde $v$ é a velocidade da luz nesse material. Como tal, $n$ será sempre maior que 1. O índice de refração do ar é aproximadamente 1.0003 e, como estamos a usar quatro algarismos significativos para as constantes, admitiremos que o índice de refração do ar é 1 (velocidade da luz no ar igual à velocidade da luz no vácuo).

Quando um raio de luz passa de um meio 1 para outro meio 2 como na figura 1.7, parte da luz é refletida no meio 1 e outra parte é refratada, passando para meio 2. O ângulo que o raio refratado faz com a perpendicular, ${\theta }_2$, é diferente do ângulo que o raio incidente faz com a perpendicular à superfície de separação entre os dois meios, ${\theta }_1$.

Mudando o ângulo ${\theta }_1$, observa-se que a relação,

designada por Lei de Snell.

A simetria da lei da reflexão (1.2) e da lei da refração (1.4), em relação à troca dos índices i e r, ou 1 e 2, mostra que se a direção dum raio de luminoso for invertida, o raio percorrerá o percurso inverso: princípio de reversibilidade.

1.4. Princípio do tempo mínimo de Fermat

Antes da era de Cristo, Hero de Alexandria explicou a lei da reflexão afirmando que o raio de luz refletido percorre o caminho mais curto entre o ponto inicial e final. Entre esses dois pontos existem outros percursos possíveis, formados por um segmento desde o ponto inicial até um ponto na superfície refletora e um segundo segmento desde esse ponto até o ponto final, mas os percursos em que os ângulos de incidência e de reflexão são diferentes conduzem a tempos maiores.

No século XVII, Pierre de Fermat estendeu esse princípio à propagação em meios com diferentes índices de refração. O princípio de Fermat estabelece que: A trajetória seguida por um raio luminoso entre dois pontos é aquela que é percorrida no menor tempo possível. No exercício 1.7 mostra-se que esse princípio conduz à lei de Snell, usando como analogia o percurso que um nadador-salvador deverá seguir para alcançar uma pessoa em dificuldades no menor tempo possível.

O que dá origem às miragens é o facto de que em dias quentes de verão a temperatura do ar é maior quanto mais próximo do solo, fazendo com que a densidade do ar diminua quanto mais próximo do solo. Com menor densidade o índice de refração também é menor.

Consideremos um raio luminoso atravessa $n$ camadas com índices de refração diferentes. Na camada em que o índice de refração é $n_i$, a velocidade da luz é $v_i=c/n_i$; a trajetória nessa camada será um segmento de reta de comprimento $s_i$ e o tempo que o raio demora a percorrer esse segmento é $s_i/v_i=n_i{s}_i/c$. O tempo total $t$ será a soma dos tempos em todas as $n$ camadas e define-se o percurso ótico, $\mathrm{\Delta }$, igual a esse tempo vezes $c$:

e, no caso em que o índice de refração varia continuamente com a posição, o somatório é substituído por um integral:

O percurso ótico é a distância que o raio percorreria no vácuo durante o mesmo intervalo de tempo entre o ponto inicial P e o ponto final Q. O comprimento do percurso real do raio luminoso é maior do que o percurso ótico. O princípio do tempo mínimo entre P e Q implica também o percurso ótico mínimo entre esses pontos.

As miragens, observadas nas estradas nos dias quentes, são devidas a que o ar quente das camadas mais baixas, próximas da estrada, têm menor densidade e menor índice de refração do que as camadas mais altas. A luz de um objeto por cima da estrada curva-se, devido a essa variação do índice de refração, e chega aos olhos dum condutor como se tivesse partido de um objeto por debaixo da estrada (figura 1.8). A curvatura dos raios luminosos fazem parecer como se houvesse um espelho sobre a estrada, que reflete os raios luminosos do objeto, produzindo uma imagem virtual, tal como num espelho.

A curvatura dos raios luminosos que atravessam regiões de ar com variações no índice de refração explica também porque conseguimos continuar a ver o Sol mesmo depois de ter descido abaixo do horizonte. Neste caso as camadas de ar menos densas, com menor índice de refração, são as que estão a maior altura na atmosfera; a menor densidade é devida à menor pressão, e não a temperatura maior como no caso da miragem. O resultado é que os raios solares curvam-se no sentido indicado na figura 1.9. Um observador na superfície da Terra vê a imagem do Sol na prolongação da tangente à curva no ponto em que o raio solar chega à superfície solar, um certo ângulo por cima do horizonte, quando o Sol está realmente por baixo do horizonte.

Tal como foi enunciado por Fermat, o princípio do tempo mínimo não é sempre correto. Existem situações em que o percurso ótico de um raio luminoso não corresponde a um valor mínimo; em algumas circunstâncias pode corresponder a um ponto de inflexão ou até a um máximo. O que sim é sempre verdadeiro é que a luz segue sempre uma trajetória para a qual o percurso ótico não varia em relação a pequenas variações dessa trajetória.

1.5. Reflexão interna total

Quando a luz passa de um meio com índice de refração maior para outro com menor índice de refração, o ângulo de refração é maior do que o ângulo de incidência. Aumentando o ângulo de incidência, chega-se a uma situação em que o ângulo de refração é igual a $\mathrm{\pi }/2$, como no lado direito da figura 1.10.

Nesse caso, o raio refratado é paralelo à superfície de separação entre os dois meios, e não chega a passar para o segundo meio. O ângulo de incidência ${\theta }_{\mathrm{c}}$ que faz com que o ângulo de refração seja igual a $\mathrm{\pi }/2$ é designado por ângulo crítico. Como o seno de $\mathrm{\pi }/2$ é igual a 1, substituindo na lei de Snell (1.4) obtém-se a expressão do ãngulo crítico em função dos índices de refração:

Observe-se que para que exista ângulo crítico é necessário que o índice de refração $n_1$ do primeiro meio seja maior do que o índice de refração $n_2$ do segundo meio. Se o ângulo de incidência for maior do que o ângulo crítico, já não existirá refração, apenas reflexão interna e, diz-se que há reflexão interna total.

O princípio de reflexão total é usado nos refratómetros, que são instrumentos usados para medir o índice de refração de uma substância, que realmente medem o ângulo crítico. Outra aplicação é na construção de prismas de reflexão total, como os da figura 1.11. No primeiro prisma, a luz que entra perpendicular a uma das faces perpendiculares do prisma, é refletida saindo na direção perpendicular à outra face perpendicular; no segundo prisma, a luz que incide perpendicular à face oposta ao ângulo reto é refletida nas outras duas faces, saindo na direção oposta à que entrou.

Para que exista reflexão total nos prismas da figura 1.11, o ângulo crítico do vidro do prisma, em relação ao ar, deverá ser menor do que ${45}^{\circ }$. Substituindo $n_2=1$ para o ar, na equação (1.7), e ${\theta }_c={45}^{\circ }$, obtém-se que o índice de refração que conduz a ângulo crítico de ${45}^{\circ }$ é $n_2=\sqrt{2}\approx 1.414$. O vidro costuma ter índice de refração maior do que esse valor e, como tal angulo crítico menor do que ${45}^{\circ }$; qualquer tipo de vidro pode ser usado para o prisma de reflexão total.

As fibras óticas são fios de vidro. Desde que a fibra não seja dobrada para além do ângulo crítico, os raios luminosos batem nas paredes interiores do fio com ângulo maior do que o ângulo crítico, sofrendo múltiplas reflexões internas, que permite transportar os raios luminosos ao longo da fibra.

1.6. Espelhos planos

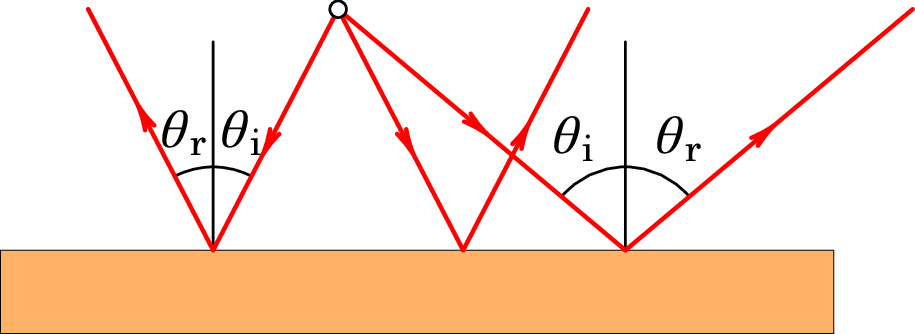
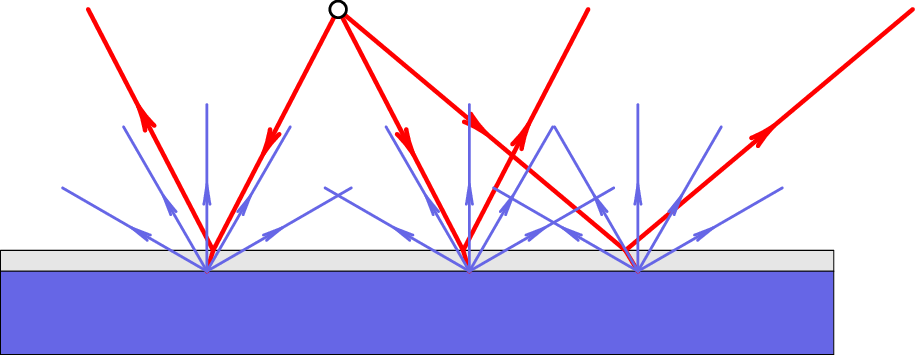
Um espelho plano é uma superfície plana e lisa, que produz unicamente reflexão especular, e não difusa. Os espelhos usados em casa costumam estar cobertos de vidro, para proteger a superfície metálica, mas vamos admitir espelhos sem nenhum vidro por cima. Como será demonstrado no exercício 1.4, qualquer ponto luminoso colocado a uma distância $d$ do espelho produz uma imagem virtual, do outro lado do espelho, à mesma distância $d$ do espelho, e na mesma reta perpendicular ao espelho que passa pelo ponto luminoso.

Cada objeto produz assim uma imagem virtual no lado oposto do espelho, sem nenhuma distorção, e com o mesmo tamanho do objeto. Uma imagem virtual pode ser observada, mas não pode ser projetada num ecrã, como a imagem real produzida numa câmara escura.

Exercícios resolvidos

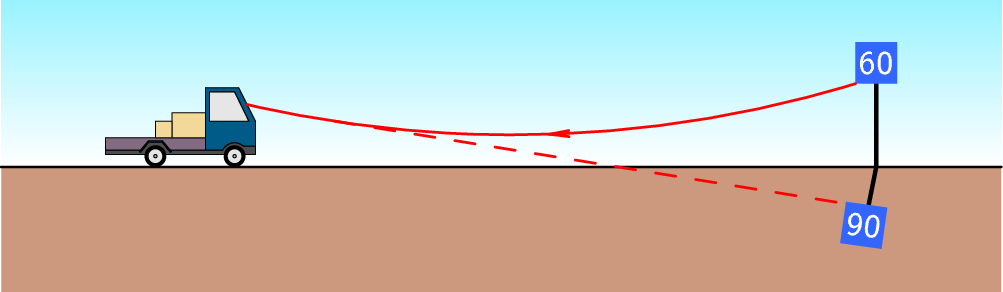
1.1. Numa câmara escura, a parede onde se forma a imagem é vertical e está a uma distância $d_{\mathrm{i}}$ do orifício. (a) Demonstre que a relação entre o tamanho ${\ell }_{\mathrm{o}}$ de um objeto vertical e o tamanho da sua imagem, ${\ell }_{\mathrm{i}}$, é igual à relação entre a distância do objeto até o orifício, $d_{\mathrm{o}}$, e a distância desde o orifício até à imagem, $d_{\mathrm{i}}$. (b) Se a distância do orifício até a imagem for igual a 90 cm, calcule o tamanho que terá a imagem do Sol (o Sol tem diâmetro de $1.394\times {10}^6$ km e está a uma distância de $149.6\times {10}^6$ km da Terra).

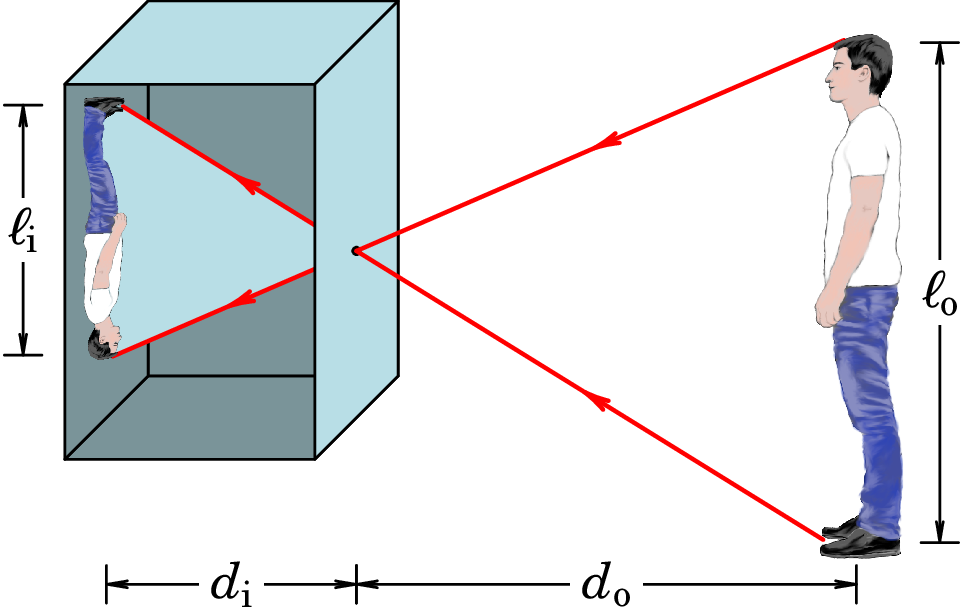
Resolução. (a) A figura acima mostra os raios que produzem as imagens dos dois extremos do objeto. como o ângulo entre esses raios é o mesmo nos dois lados do orifício, o triângulo formado pelo objeto e o orifício é semelhante ao triângulo formado pela imagem e o orifício. A semelhança de triângulos implica:

(b) Substituindo na expressão da alínea anterior a distância até o Sol, $d_{\mathrm{o}}$, o tamanho do Sol, ${\ell }_{\mathrm{o}}$, e a distância até a imagem, $d_{\mathrm{i}}=90$ cm, obtém-se:

o resultado anterior pode ser corroborado experimentalmente, e mostra que a luz propaga-se em linha reta até a distâncias tão elevadas como a distância da Terra ao Sol.

1.2. Um raio de luz, no ar, entra na água com um ângulo de incidência de 30${}^{\circ }$. Sabendo que o índice de refração da água é 1.333, determine o ângulo de refração.

Resolução. Aplicando a lei de Snell, com índices de refração $n_1=1.00$, para o ar, e $n_2=1.333$, para a água, temos:

e o valor do ângulo de refração é:

1.3. A figura mostra um método gráfico para determinar o ângulo de refração de um raio de luz que passa de um meio para outro.

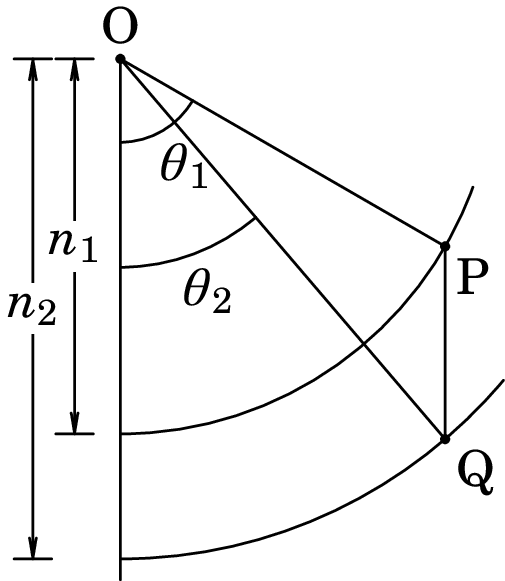
Desde um centro comum O traçam-se dois arcos de círculo com raios proporcionais aos índices de refração $n_1$ e $n_2$ dos dois meios, e uma reta que representa a normal à interface entre os meios. A seguir, traça-se o segmento OP, com um ângulo ${\theta }_1$ igual ao ângulo de incidência do raio no meio 1. Traça-se o segmento PQ, paralelo à normal entre os dois meios. O ângulo ${\theta }_2$ que o segmento PQ faz com a normal entre os dois meios é igual ao ângulo de refração. Demonstre que com essa construção geométrica, os ângulos ${\theta }_1$ e ${\theta }_2$ verificam a lei de Snell.

Resolução. A figura seguinte mostra os dois triângulos retângulos com hipotenusas OP e OQ, iguais aos índices de refração $n_1$ e $n_2$ dos dois meios, e um dos catetos na direção da normal ao meio, OS.

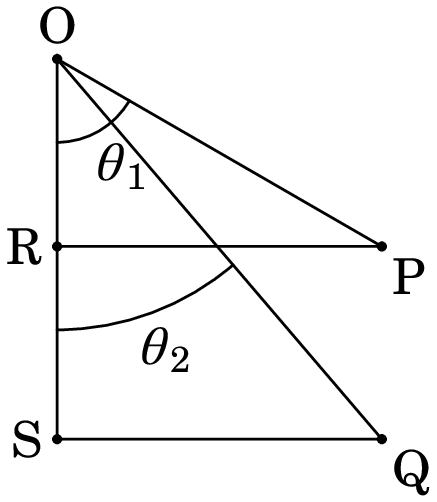
Os comprimentos dos catetos RP e SQ são,

Como RS é paralelo a PQ, então $\mathrm{R}\mathrm{P}=\mathrm{S}\mathrm{Q}$, e igualando as duas expressões anteriores obtém-se a lei de Snell:

1.4. Demostre que qualquer ponto luminoso próximo de um espelho plano produz uma imagem virtual, no outro lado do espelho, e que a distância desde o ponto (objeto) até à superfície do espelho, $d_{\mathrm{o}}$, é igual à distância $d_{\mathrm{i}}$, desde a imagem até à superfície do espelho.

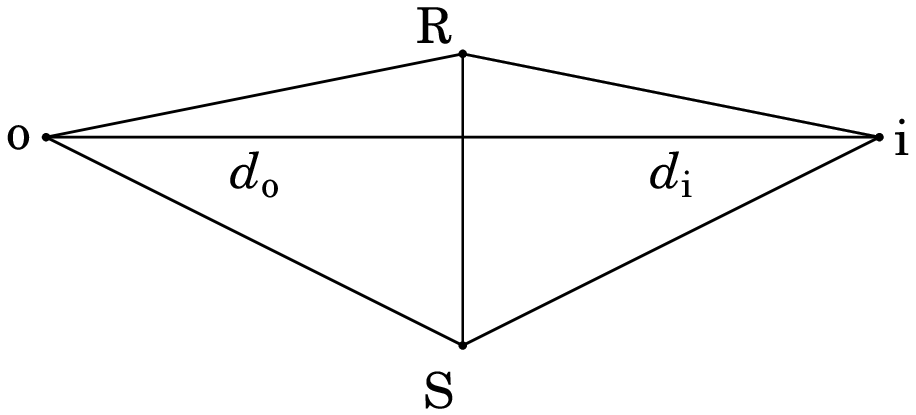
Resolução. A figura seguinte mostra dois raios de luz que saem do ponto luminoso o, sendo refletidos no espelho, nos pontos R e S.

Os dois raios refletidos em R e em S parecem vir do ponto comum i, no outro lado do espelho. Os ângulos de incidência e reflexão do raio em R são iguais, e são iguais também ao ângulo que o segmento RI faz com a perpendicular ao espelho ($\alpha$ na figura). E os ângulos de incidência e reflexão do raio em S são iguais, e são iguais também ao ângulo que o segmento SI faz com a perpendicular ao espelho ($\beta$ na figura). Os ângulos $\zeta$ e $\eta$ são ambos iguais a ${90}^{\circ }-\alpha$ e, como tal $\zeta =\eta$. De forma semelhante, $\varphi =\psi$, porque ambos ângulos são iguais a ${90}^{\circ }-\beta$. A igualdade da base, RS, e dos dois ângulos nessa base, implica que os dois triângulos, ORS e IRS, são semelhantes. As distâncias do ponto e da sua imagem até a superfície do espelho ($d_{\mathrm{o}}$ e $d_{\mathrm{i}}$) são as alturas desses triângulos, que são iguais, porque os triângulos são semelhantes:

Como não assumimos nenhum ângulo especial $\alpha$ ou $\beta$, quaisquer outros dois raios que considerarmos formarão outros dois triângulos semelhantes com altura $d_{\mathrm{o}}$ (igual a $d_{\mathrm{i}}$). A conclusão é que todos os raios refletidos no espelho parecem vir dum ponto único i, imagem de o, que está à mesma distância do espelho do que o ponto o.

1.5. Qual é a altura mínima que deverá ter um espelho vertical para que uma pessoa consiga ver a imagem do seu corpo completo, e como deverá ser posicionado?

Resolução. A figura seguinte mostra um homem, no lado direito de um espelho plano e vertical, e a sua imagem no lado esquerdo do espelho.

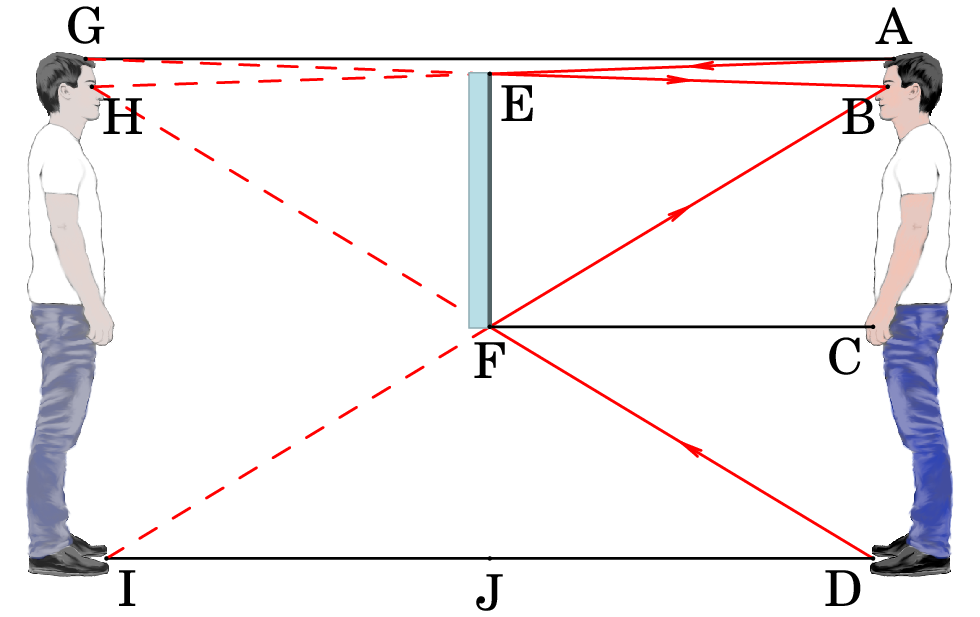
Para que o homem possa ver a sua imagem completa, deverá poder ver os raios DFB e AEB, que partem da parte mais baixa dos seus pés, e da parte mais alta do seu cabelo, e chegam aos seus olhos em B. O tamanho mínimo do espelho deverá ser então a distância entre E e F, onde esses dois raios são refletidos no espelho.

A altura do ponto F, desde o chão, é FJ, igual a CD, que é metade da altura dos olhos B do homem: FJ=BD/2. E a altura do ponto E é EJ, igual à altura do homem, AD, menos metade da distância AB entre os olhos e o ponto mais alto A: EJ=AD-AB/2. O tamanho mínimo do espelho é:

que é exatamente metade da altura do homem.

A posição onde debe ser colocado o espelho é o o seu ponto mais baixo à altura HI, ou seja, a uma altura igual a metade da altura dos olhos do homem.

1.6. Um peixe está nadar a 1 m por debaixo da superfície da água. Determine a que profundidade parece estar a nadar o peixe, quando visto por uma pessoa fora da água.

Resolução. A figura seguinte mostra dois raios luminosos que partem de um ponto "o" no peixe: um primeiro raio vertical, perpendicular à superfície da água, que atravessa para o ar sem ser desviado, e um segundo raio que atinge a superfície da água a um ângulo ${\theta }_2$ com a vertical, e sai para o ar formando um ângulo ${\theta }_1$ com a vertical.

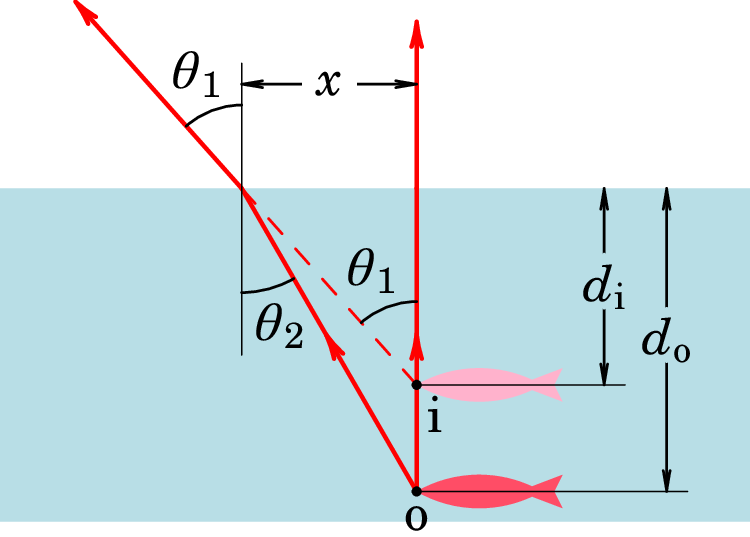
A imagem "i" do ponto "o" encontra-se na interseção entre a prolongação do raio que sai da água com ângulo ${\theta }_1$, e o raio vertical. Os raios mais luminosos, que contribuem mais para a formação da imagem, são os que estão mais próximos da vertical ($x$ próximo de zero). Como tal, podemos admitir que os ângulos ${\theta }_1$ e ${\theta }_2$ são suficientemente pequenos para podermos aproximar o seno desses ângulos pelas sua tangentes, que podem ser calculadas a partir das distâncias $x$, $d_{\mathrm{o}}$ e $d_{\mathrm{i}}$ na figura:

enquanto que o seno do ângulo ${\theta }_1$ é aproximadamente,

Substituindo esses senos na lei de Snell (1.4), obtém-se:

onde $n_1=1$ é o índice de refração do ar, $n_2=1.333$ é o índice de refração da água e $d_o=1$ m é a profundidade à que se encontra o peixe. O valor obtido para a profundidade da imagem do peixe é:

1.7. No ponto A de uma praia encontra-se um nadador-salvador, enquanto que num ponto B do mar encontra-se um banhista em dificuldades (ver figura). O nadador-salvador corre na praia a uma velocidade $v_{\mathrm{p}}$ e nada no mar a uma velocidade menor, $v_{\mathrm{m}}$. Qual a trajectória que o nadador-salvador deve seguir, desde A, para chegar o mais rapidamente possível ao banhista em B?

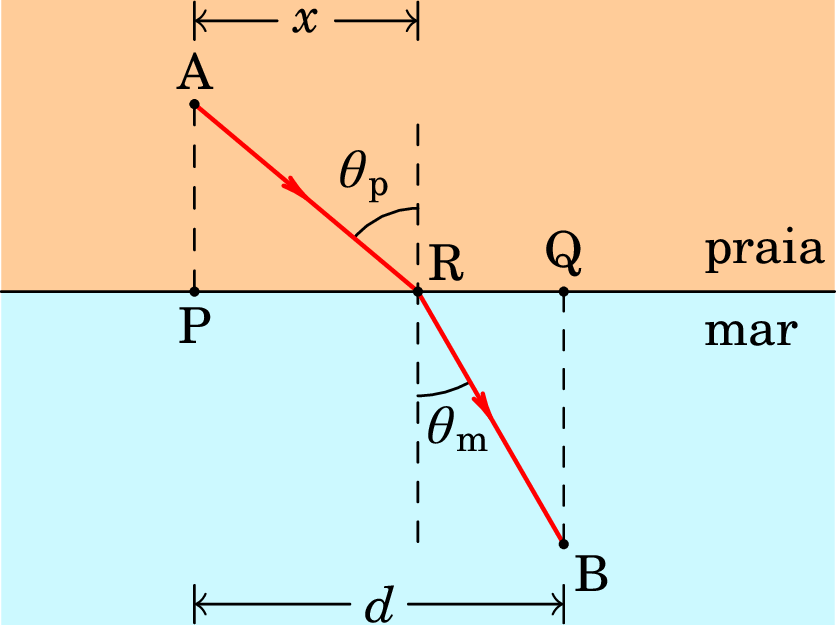
Resolução. Não há duvida que se os pontos inicial e final estão ambos na praia ou ambos no mar, a trajetória mais rápida é um segmento de reta. Como tal, a trajetória ótima desde A até B serão dois segmentos de reta, um na praia e outro no mar. Mas os esses dois segmentos, AR e BR na figura acima, não têm de ser parte dum mesmo segmento de reta entre A e B. O ponto R encontra-se $x$ unidades à direita de B, e o valor ótimo de $x$ é o que faz com que o tempo desde A até B seja mínimo.

A distância que o nadador-salvador percorre na praia é a hipotenusa do triângulo APR, igual a,

e o tempo $t_{\mathrm{p}}$ do percurso na praia, desde A até R, é:

De forma semelhante, a distância percorrida no mar é a hipotenusa do triângulo BQR e o tempo necessário para percorrer essa distância é:

Como as distâncias AP, BQ, $d$ e as velocidades $v_{\mathrm{p}}$ e $v_{\mathrm{m}}$ têm valores fixos (não dependem da posição do ponto R), a expressão do tempo total, $t=t_{\mathrm{p}}+t_{\mathrm{m}}$ em função da variável $x$ é a seguinte:

E o valor de $x$ que faz com que $t$ seja mínimo obtém-se derivando a expressão anterior e igualando o resultado a zero:

e como as expressões nas raízes quadradas são as hipotenusas dos dois triângulos retângulos, obtém-se:

$x/AR$ é igual ao seno do ângulo ${\theta }_{\mathrm{p}}$ (ver gráfico acima), e $(d-x)/RB$ é o seno de ${\theta }_{\mathrm{m}}$; podemos também multiplicar os dois lados da equação por $v$, que é a velocidade máxima que o nadador atinge quando corre numa pista de corridas. Como tal, o tempo será mínimo quando a relação entre os dois ângulos for:

que é idêntica à lei de Snell para os raios de luz. Neste caso os números $v/v_{\mathrm{p}}$ e $v/v_{\mathrm{p}}$ são iguais à relação entre a velocidade máxima do nadador e a sua velocidade na areia da praia ou na água do mar.

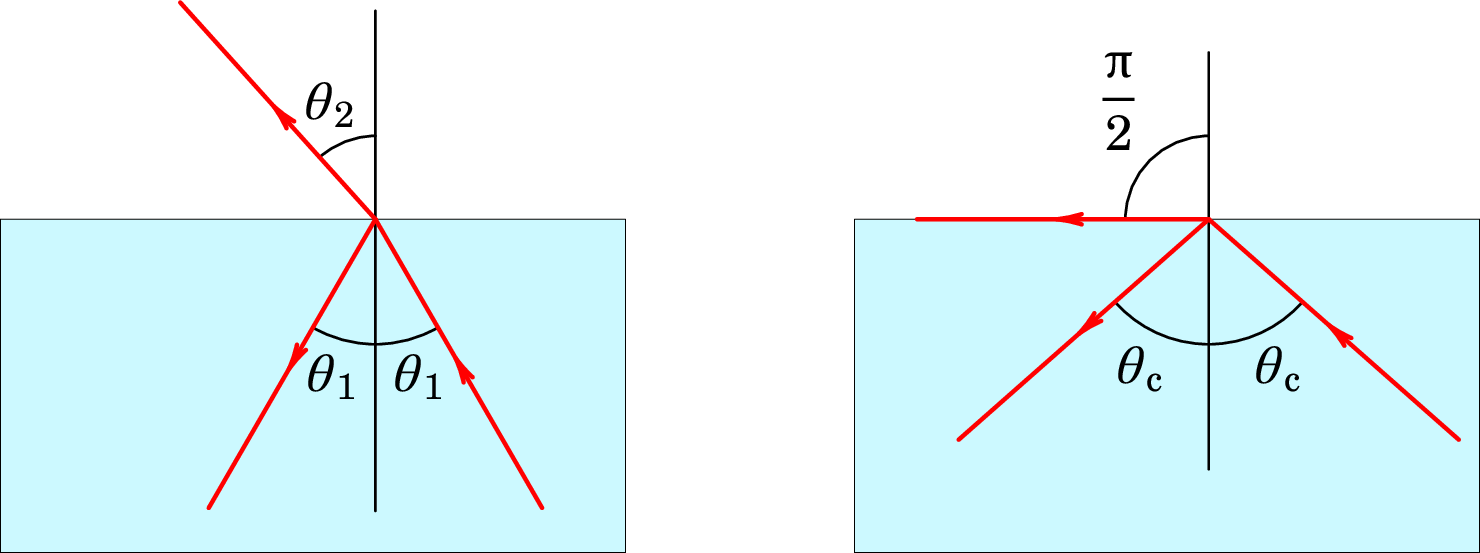
1.8. Determine o ângulo crítico para a luz que passa de vidro, com índice de refração 1.56, para água, com índice de refração 1.333.

Resolução. Usando a lei de Snell, com ângulo de incidência ${\theta }_{\mathrm{c}}$ e ângulo de refração igual a 90${}^{\circ }$,

1.9. Uma placa de vidro tem 3 cm de espessura e índice de refração de $1.5$. Determine o deslocamento lateral de um raio luminoso que incide na superfície da placa com ângulo de incidência de ${50}^{\circ }$.

Resolução. Como pode ver-se na figura seguinte, o ângulo de refração ${\theta }_2$ do raio quando penetra no vidro é o mesmo ângulo com que incide no outro lado, quando sai novamente para o ar. Como tal, o ângulo de refração do raio quando sai para o ar é o mesmo ângulo ${\theta }_1$ com que entrou na placa, e os raios que entram e saem na placa são paralelos.

O desvio lateral é a distância $d$ entre a prolongação do raio que entra e o raio que sai da placa; $d$ é também igual ao cateto QR no triângulo retângulo PQR. Como o ângulo no vértice P desse triângulo é igual a ${\theta }_1-{\theta }_2$, o cateto oposto é igual a:

No triângulo PQS, a hipotenusa é igual a:

E substituindo na equação anterior,

Neste caso ${\theta }_1={50}^{\circ }$, e substituindo o índice de refração do ar, $n_1=1$, e o índice de refração do vidro, $n_2=1.5$, na lei de Snell, obtém-se:

e o desvio lateral do feixe é:

Exercícios adicionais

1.11. Considere uma pessoa que se encontra imersa numa piscina com água (n = 1.333). A pessoa vê objectos num círculo de raio R = 2.0 m por cima da sua cabeça e fora deste círculo a pessoa repara que a cor da água é da cor das paredes da piscina. A que profundidade se encontra a pessoa?

1.12. Um homem caminha a 1.3 m/s, aproximando-se de um espelho plano. Com que velocidade se aproximará a sua imagem dele?

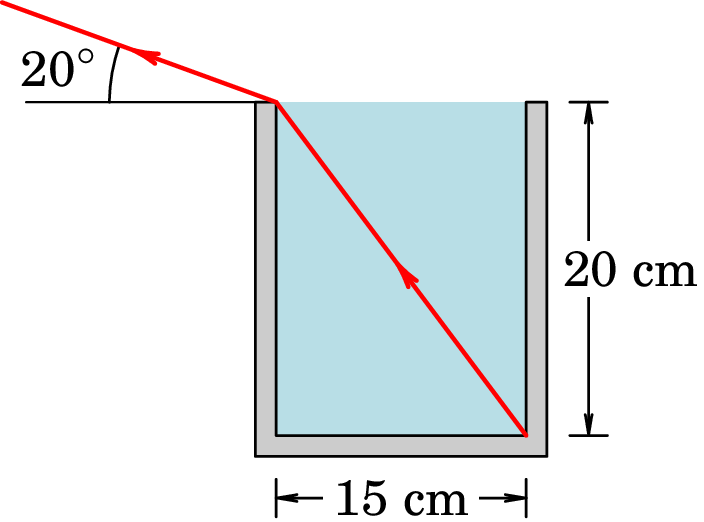
1.13. Para medir o índice de refração de um líquido, preenche-se completamente com esse líquido um recipiente retangular de 15 cm de lado e 20 cm de profundidade, e determina-se que o mínimo ângulo por cima da horizontal em que é possível observar o canto inferior do recipiente é de ${20}^{\circ }$. Com essa informação, calcule o índice de refração do líquido.

Respostas dos exercícios adicionais

1.11. $1.76$ m.

1.12. 2.6 m/s.

1.13. 1.566.