Numa esfera condutora isolada, a carga distribui-se uniformemente na superfície. Se o raio da esfera é e a carga total , então a densidade superficial de carga é constante e igual à carga total dividida pela área da superfície da esfera
Para calcular o campo elétrico num ponto P qualquer, que está a uma distância do centro da esfera, é conveniente definir o eixo dos com origem O no centro da esfera e passando pelo ponto P, como se mostra na figura B.1
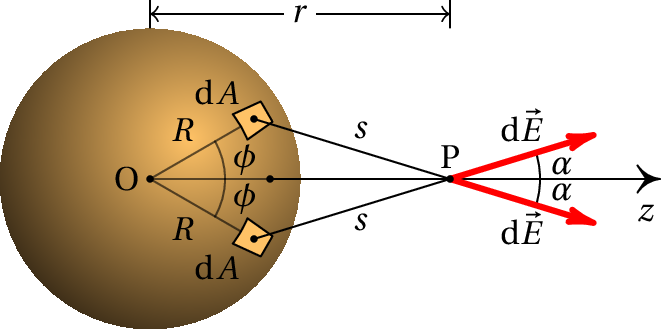
Divide-se a superfície da esfera em muitos pedaços infinitesimalmente pequenos, calcula-se o campo produzido por cada pedaço no ponto P e o campo total é a sobreposição de todos esses campos. A figura B.1 mostra duas partes infinitesimais da superfície da esfera, ambas com área , em dois pontos que estão à mesma distância de P, de forma que os segmentos desde esses pontos até P estão no mesmo plano com o eixo dos . Um desses pontos tem coordenadas polares ( , , ), e o outro ( , , ), onde é o ângulo indicado na figura. O ângulo mede-se no plano , perpendicular ao eixo dos
O elemento infinitesimal de área, , determina-se multiplicando os comprimentos dos dois arcos obtidos quando os dois ângulos, e , aumentam infinitesimalmente em e . O aumento do ângulo produz um arco de comprimento , e o aumento do ângulo produz um arco que, projetado no plano , tem raio e ângulo . Como tal, o elemento infinitesimal de área na superfície da esfera é
A carga infinitesimal nessa região obtém-se multiplicando essa área pela carga superficial (equação B.1)
Essa carga infinitesimal pode ser considerada uma carga pontual e, assim sendo, o módulo do campo que ela produz no ponto P é dado pela expressão do campo para uma carga pontual (equação 1.5)
onde é a distância desde a região infinitesimal na superfície da esfera, até o ponto P. Os campos produzidos pelas duas regiões infinitesimais mostradas na figura B.1 têm o mesmo módulo (equação B.4) e fazem o mesmo ângulo em relação ao eixo , mas nos dois lados opostos do eixo dos . Como tal, as componentes desses dois campos perpendiculares ao eixo dos anulam-se, ficando apenas a soma das componentes paralelas ao eixo dos . Conclui-se então que o campo total deverá ser na direção do eixo dos e para o calcular basta integrar a componente , do campo produzido pela região infinitesimal no ( , , ), em ordem a e a , com os limites necessários para incluir todos os pontos da superfície:
Como e dependem de mas não dependem de , o integral em ordem a é simplesmente igual a
Este integral é mais simples de calcular expressando os dois ângulos e em função da distância , usando o teorema do cosseno aplicado ao triângulo de lados , e na figura B.1
A expressão para obtém-se a partir da equação B.7
Lembre-se que e são constantes para todos os segmentos da superfície esférica. A expressão para obtém-se derivando a equação B.8
Substituindo as expressões B.9 e B.10 na equação B.6 obtém-se
Onde e são os valores mínimo e máximo da distância , em e . O resultado do integral é
É necessário considerar dois casos diferentes, quando o ponto P está dentro ou fora da esfera. Quando o ponto P está dentro da esfera, , e, como tal, e
Ou seja, o campo elétrico em qualquer ponto dentro da esfera é nulo. Fora da esfera, , e
Que é o mesmo campo produzido por uma carga pontual colocada no centro da esfera. Resumindo, o campo da esfera condutora é na direção radial, atrativo se ou repulsivo se e com módulo igual a
A figura fig-B.2 mostra duas esferas condutoras concêntricas isoladas, de raios e . A esfera de raio tem carga total , a esfera de raio tem carga total e . O campo de cada uma das esferas é dado pela expressão obtida na secção anterior e o campo total é a soma desses dois campos.
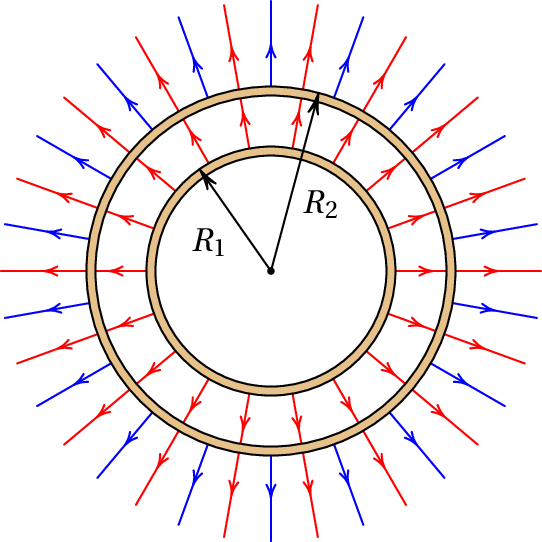
No interior da esfera menor, o campo é nulo porque todos os pontos nessa região encontram-se no interior das duas esferas e as esferas condutoras não produzem campo no seu interior. Nos pontos que estão entre as duas esferas, o campo é igual ao campo da esfera menor, porque esses pontos estão no interior da esfera maior, onde esta não produz nenhum campo. Nos pontos fora das duas esferas, o campo total é igual à soma dos campos das duas esferas, ou à sua diferença, segundo e tenham o mesmo sinal ou sinais opostos.
A expressão para o módulo do campo total a uma distãncia do centro das esferas é então
O campo é sempre na direção radial. Entre as duas esferas, o campo aponta no sentido radial se é positiva, ou no sentido oposto se é negativa. Fora das duas esferas, o campo é repulsivo se é positiva, ou atrativo se é negativa.
As expressões obtidas neste apêndice para o campo da esfera condutora e das duas esferas concêntricas podem ser obtidas mais facilmente usando a lei de Gauss, como se explica no capítulo 6. No entanto, o método usado neste apêndice é mais geral e permite obter campos de distribuições de carga mais complicadas. O problema é que os integrais obtidos podem não ter solução analítica, tendo de ser calculados de forma numérica.