História das teorias da Luz

Ondas eletromagnéticas

Cada possível solução das equações de onda dos campos E e B é uma onda eletromagnética. Os dois campos não são independentes, porque o rotacional de cada um é proporcional à derivada do outro em função do tempo. Isso implica que E e B em qualquer ponto são sempre perpendiculares,

A direção em que a onda se propaga é a direção em que transporta energia, que é a direção do vetor de Poynting:

S = E × B 4 π k m

Como tal, os campos E e B são perpendiculares à direção de propagação. Pode mostrar-se que em cada ponto os dois campos devem ser também perpendiculares entre si.

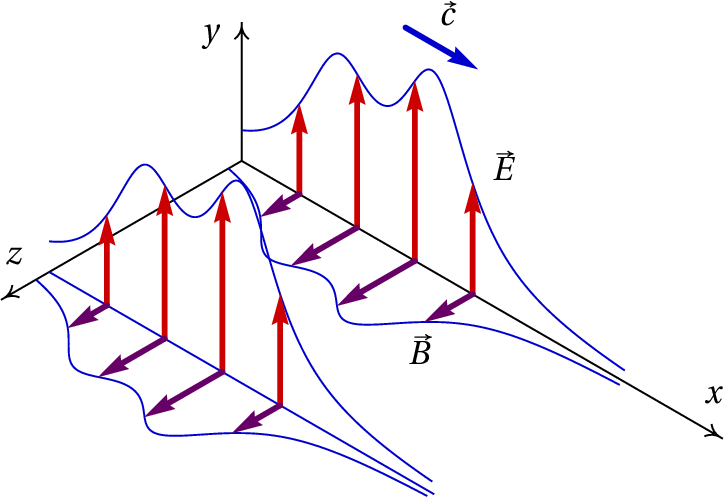
Ondas planas polarizadas

Correspondem ao caso em que as direções dos campos são as mesmas em qualquer ponto. Os eixos y e z nas direções de E e B , a onda propaga-se no sentido positivo do eixo x . As equações de Maxwell conduzem a:

∂ 2 E ∂ t 2 = c 2 ∂ 2 E ∂ x 2 ∂ 2 B ∂ t 2 = c 2 ∂ 2 B ∂ x 2 B = E c

e a solução geral é:

E = f ( x − c t ) + g ( x + c t ) B = 1 c f ( x − c t ) − 1 c g ( x + c t )

Em que f e g são duas funções quaisquer. A figura seguinte mostra uma possibilidade, com g = 0 :

Campos numa onda eletromagnética plana