Uma onda eletromagnética propaga-se no vácuo, no sentido positivo do eixo dos . No instante , o campo elétrico em função de é dado pela função (unidades SI)
Como a onda propaga-se no sentido positivo do eixo dos , a função de onda do campo elétrico deverá ser da forma , onde é a velocidade da luz no vácuo. No instante a expressão do campo em função de é e, comparando com a função dada no enunciado, conclui-se que
Como tal, a função de onda do campo elétrico é:
Substituindo os valores dados de e e o valor de , em unidades SI, na equação de onda. obtém-se o valor do campo:
Uma lâmina metálica muito extensa encontra-se sobre o plano O . A lâmina é ligada a uma fonte variável que produz um campo elétrico uniforme no plano O , mas variável no tempo segundo a equação: , onde e são constantes. O campo elétrico na lâmina origina uma onda eletromagnética plana. Escreva as funções que representam os campos elétrico e magnético dessa onda, em função do tempo e da posição.
A onda plana produzida estará a sair do plano O para os dois lados. Ou seja, propagar-se-á no sentido positivo do eixo dos na região , e no sentido negativo do eixo dos na região . Como tal, a função de onda para o campo elétrico terá a forma:
Em = 0 obtém-se , que deverá ser igual ao valor do campo elétrico na lâmina:
Substituindo e , as expressões das funções e são:
Em , , e a função de onda do campo elétrico será então:
A função de onda do campo magnético deverá ser igual à do campo elétrico, dividida pela velocidade da luz; como tal,
O campo elétrico será na direção de em todo o espaço. Na região , como a velocidade é segundo , o campo magnético deverá estar na direção e sentido de (o produto vetorial do campo elétrico pelo campo magnético deverá ser na direção e sentido da velocidade). Na região , como a velocidade é segundo , o campo magnético deverá estar na direção de . As expressões vetoriais dos campos são então:
A figura representa o campo eletromagnético de uma onda plana de 420 MHz, no instante = 0. As linhas de campo verticais representam o campo elétrico e as linhas perpendiculares à figura são as linhas do campo magnético. Calcule a distância e escreva o vetor do campo magnético em função do tempo e da coordenada .
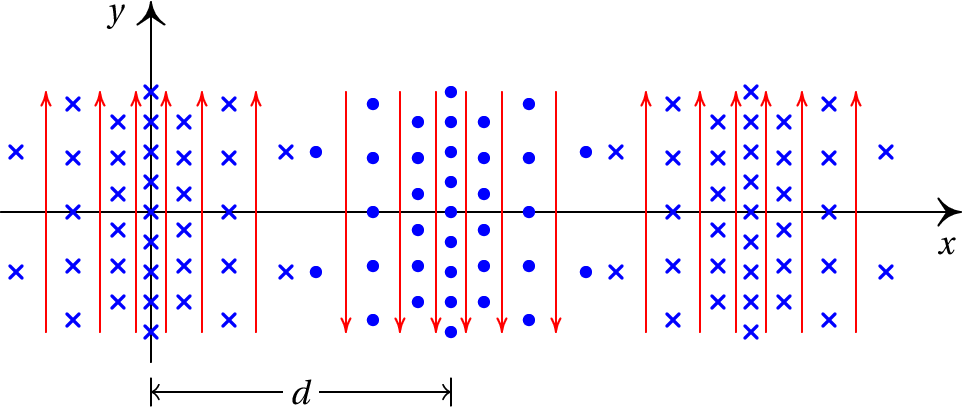
Num ponto qualquer, por exemplo na origem, o produto vetorial do campo elétrico com o campo magnético é na direção de propagação da onda; com os dados da figura, esse produto fica na direção do eixo dos , no sentido negativo.
O facto de ter uma frequência específica, indica que a onda é harmónica. Como tal, a equação da onda de cada campo deverá ter a forma da expressão 12.31 mas trocando o sinal negativo por positivo, já que a onda progaga-se no sentido negativo do eixo dos :
Em = 0 e = 0, . Como o gráfico mostra que em = 0 e = 0 o valor de é mínimo, conclui-se que ; usando a identidade , temos:
Em unidades SI, o período é,
e o comprimento de onda é:
A distância é metade do comprimento de onda:
Substituindo os valores do período e o comprimento de onda, a expressão do campo magnético é (unidades SI):