Introdução à computação quântica

Jaime Villate. Faculdade de Engenharia da Universidade do Porto

7. Qbits

Um qbit (quantum bit) é um sistema físico com apenas dois estados próprios, | 0 〉 e | 1 〉 . O estado geral do qbit é uma sobreposição dos dois estados próprios:

| Ψ 〉= Ψ 1 | 0 〉+ Ψ 2 | 1 〉

em que Ψ 1 e Ψ 2 são dois números complexos quaisquer, sujeitos unicamente à condição de normalização:

| Ψ 1 | 2 +| Ψ 2 | 2 = 1

Os números reais | Ψ 1 | 2 e | Ψ 2 | 2 são as probabilidades do estado ser um dos estados próprios | 0 〉 ou | 1 〉 .

Representação matricial

As operações nos estados dos qbits podem ser feitas na representação matricial em que cada estado próprio é representado por uma matriz de uma coluna e duas linas:

| 0 〉= 10 | 1 〉= 01

Como tal, o estado de um qbit é uma matriz coluna com dois números complexos:

| Ψ 〉= Ψ 1 10 + Ψ 2 01 = Ψ 1 Ψ 2

O "bra" correspondente ao "ket" | Ψ 〉 é uma matriz com uma linha e dois colunas:

〈 Ψ |= Ψ ∗ 1 Ψ ∗ 2

Produto escalar

O produto escalar entre dois estados | Ψ 〉= Ψ 1 | 0 〉+ Ψ 2 | 1 〉 e | Φ 〉= Φ 1 | 0 〉+ Φ 2 | 1 〉 , representado por 〈 Ψ | Φ 〉 , é um número complexo. Na representação matricial, obtém-se usando o produto entre matrizes:

〈 Ψ | Φ 〉= Ψ ∗ 1 Ψ ∗ 2 Φ 1 Φ 2 = Ψ ∗ 1 Φ 1 + Ψ ∗ 2 Φ 2 =〈 Φ | Ψ 〉 ∗

A condição de normalização implica que o produto escalar de qualquer estado com si próprio deverá ser igual a 1:

〈 Ψ | Ψ 〉= | Ψ 1 | 2 +| Ψ 2 | 2 = 1 〈 Φ | Φ 〉= | Φ 1 | 2 +| Φ 2 | 2 = 1

Operadores

No caso de um cbit, mostraram-se na secção anterior os 4 possíveis operadores, f 0 , f 1 , f 2 e f 3 . No caso dos qbits, há un número infinito de possíveis operadores. Na representação matricial, os operadores ˆ U são as matrizes quadradas com duas colunas e duas linhas:

ˆ U = u 11 u 12 u 21 u 22

onde os quatro números complexos u i j devem verificar as seguintes condições, que fazem com que a matriz de ˆ U seja unitária:

ˆ U † ˆ U = u ∗ 11 u ∗ 21 u ∗ 12 u ∗ 22 u 11 u 12 u 21 u 22 = 10 0 1 ⇐⇒ ⎧⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎩ | u 11 | 2 +| u 21 | 2 = 1 | u 12 | 2 +| u 22 | 2 = 1 u ∗ 11 u 12 + u ∗ 21 u 22 = 0 u 11 u ∗ 12 + u 21 u ∗ 22 = 0

Ou seja, cada coluna na matriz de ˆ U deve representar um possível estado e o produto escalar entre os estados correspondentes às duas colunas deverá ser nulo.

Quando o operador atua no estado | Ψ 〉 do qbit, o resultado é outro estado | Φ 〉 :

| Φ 〉= ˆ U | Ψ 〉= u 11 u 12 u 21 u 22 Ψ 1 Ψ 2 = u 11 Ψ 1 + u 12 Ψ 2 u 21 Ψ 1 + u 22 Ψ 2

A ação do operador ˆ U também costuma representar-se de forma gráfica com o seguinte diagrama:

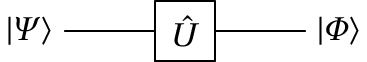
one qbit operator

A linha do lado esquerdo representa o estado inicial (entrada) e a linha do lado direito é o estado final (saída), após a ação do operador ˆ U .

Nas secções seguintes mostram-se o diagrama e a matriz de alguns operadores importantes.

X de Pauli

X de Pauli ˆ X = 01 1 0

Y de Pauli

Y de Pauli ˆ Y = 0 − ii 0

Z de Pauli

Z de Pauli ˆ Z = 10 0 − 1

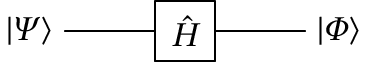
Hadamard

Hadamard ˆ H = 1 2 11 1 − 1

No caso das 3 matrizes de Pauli, se a entrada for um dos estados próprios | 0 〉 ou | 1 〉 , a saída será também um estado próprio, multiplicado por uma constante com módulo igual a 1. No caso do operador de Hadamard, se a entrada for um dos estados próprios | 0 〉 ou | 1 〉 a saída será uma sobreposição dos dois estados próprios, ambos com a mesma probabilidade de 1/2:

ˆ H | 0 〉= 1 2( | 0 〉+ | 1 〉 )ˆ H | 1 〉= 1 2( | 0 〉− | 1 〉 )