Introdução à computação quântica

Jaime Villate. Faculdade de Engenharia da Universidade do Porto

8. Sistemas com vários qbits

2 qbits

No caso de dois qbits há 4 estados próprios, correspondentes aos 4 possíveis valores que podem ser representados com 4 cbits. O estado do sistema de 2 qbits será qualquer combinação linear desses 4 estados próprios:

| Υ 〉= Υ 1 | 00 〉+ Υ 2 | 01 〉+ Υ 3 | 10 〉+ Υ 4 | 11 〉

em que os quatro números complexos Υ i verificam a condição de normalização:

| Υ 1 | 2 +| Υ 2 | 2 +| Υ 3 | 2 +| Υ 4 | 2 = 1

Os quatro números reais | Υ i | 2 são as probabilidades do estado ser um dos quatro estados próprios (valores possíveis de dois cbits). Os valores possíveis dos dois cbits podem ser representados por matrizes de uma coluna e quatro linhas:

| 00 〉= ⎡⎢ ⎢ ⎢ ⎣ 10 0 0 ⎤⎥ ⎥ ⎥ ⎦ | 01 〉= ⎡⎢ ⎢ ⎢ ⎣ 01 0 0 ⎤⎥ ⎥ ⎥ ⎦ | 10 〉= ⎡⎢ ⎢ ⎢ ⎣ 00 1 0 ⎤⎥ ⎥ ⎥ ⎦ | 11 〉= ⎡⎢ ⎢ ⎢ ⎣ 00 0 1 ⎤⎥ ⎥ ⎥ ⎦

Como tal, o estado do sistema é representado por uma matriz coluna com quatro números complexos:

| Υ 〉= ⎡⎢ ⎢ ⎢ ⎣ Υ 1 Υ 2 Υ 3 Υ 4 ⎤⎥ ⎥ ⎥ ⎦

Produto tensorial

Um caso particular do estado de 2 qbits é quando o estado do primeiro qbit for | Ψ 〉= Ψ 1 | 0 〉+ Ψ 2 | 1 〉 , independente do estado | Φ 〉= Φ 1 | 0 〉+ Φ 2 | 1 〉 do segundo qbit. Nesse caso, o estado do sistema dos dois qbits é igual ao produto tensorial dos dois kets:

| Φ 〉| Ψ 〉= ( Φ 1 | 0 〉+ Φ 2 | 1 〉 )( Ψ 1 | 0 〉+ Ψ 2 | 1 〉 ) = Φ 1 Ψ 1 | 00 〉+ Φ 1 Ψ 2 | 01 〉+ Φ 2 Ψ 1 | 10 〉+ Φ 2 Ψ 1 | 11 〉

Observe-se que no produto tensorial entre kets o ket do primeiro qbit coloca-se na segunda posição e o segundo na primeira posição. O produto tensorial entre dois cbits (estados próprios) obtém se juntado os dois cbits num só ket.

Na representação matricial, usaremos o operador ⊗ para o produto tensorial, para distingui-lo do produto matricial. O produto tensorial entre matrizes obtém-se multiplicando cada elemento da primeira matriz, pela segunda matriz:

| Φ 〉| Ψ 〉= Φ 1 Φ 2 ⊗ Ψ 1 Ψ 2 = ⎡⎢ ⎢ ⎢ ⎣ Φ 1 Ψ 1 Φ 1 Ψ 2 Φ 2 Ψ 1 Φ 2 Ψ 2 ⎤⎥ ⎥ ⎥ ⎦

Observe-se que as condições de normalização dos kets | Ψ 〉 e | Φ 〉 , implicam a normalização do produto tensorial | Φ 〉| Ψ 〉 .

| Φ 1 Ψ 1 | 2 +| Φ 1 Ψ 2 | 2 +| Φ 2 Ψ 1 | 2 +| Φ 2 Ψ 2 | 2 = | Φ 1 | 2 +| Φ 2 | 2 | Ψ 1 | 2 +| Ψ 2 | 2 = 1

Operadores de 2 qbits

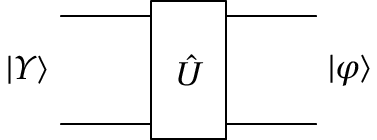
A figura mostra o diagrama de circuito para os operadores de 2 qubits. A linha de cima representa o primeiro qbit e a linha de baixo o segundo. O estado dos qbits de entrada, | Υ 〉 , é multiplicado por um operador unitário ˆ U , produzindo o estado dos qbits de saída | ϕ 〉 . Na representação matricial, ˆ U é uma matriz complexa, unitária, com 4 linhas e quatro colunas.

two qbits operator | ϕ 〉= ˆ U | Υ 〉

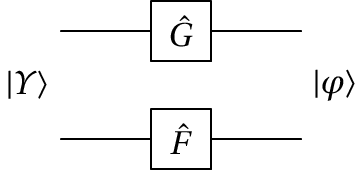
Um caso particular é a combinação de dois operadores de 1 qubit, cada um a atuar num dos dois qbits. A matriz correspondente seria o produto tensorial das duas matrices, 2 por 2, desses operadores de 1 qbit.

two one qbit operators | ϕ 〉= ˆ F ⊗ ˆ G | Υ 〉

Observe-se a ordem dos operadores no produto tensorial. Primeiro o operador que atua no segundo qbit e depois o que atua no primeiro qbit.

Não controlado

O operador mais importante de 2 qubits, porque pode ser usado em combinação com operadores de um qbit para obter outros operadores de 2 qbits, é o chamado controlled-NOT (não controlado), ou simplesmente cNOT. Existem dois desses operadores, designados de ˆ C 12 e ˆ C 21 . Os diagramas de circuito e matrizes desses dois operadores são os seguintes:

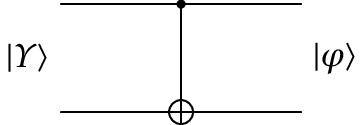
Controlled-NOT 12 ˆ C 12 = ⎡⎢ ⎢ ⎢ ⎣ 10 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ⎤⎥ ⎥ ⎥ ⎦

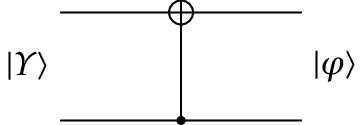
Controlled-NOT 21 ˆ C 21 = ⎡⎢ ⎢ ⎢ ⎣ 10 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ⎤⎥ ⎥ ⎥ ⎦

O efeito de ˆ C 12 nos 4 estados próprios | n 1 n 0 〉 ( n 1 e n 0 iguais a 0 ou 1) é o seguinte: o primeiro cbit (o último algarismo n 0 ) fica igual; o segundo cbit ficará igual se o primeiro cbit for igual a 0, mas mudará se o primeiro cbit for igual a 1. Ou seja, o segundo cbit fica igual ao resultado dum ou exclusivo entre os dois cbits. O primeiro cbit, que não muda, diz-se que é o cbit de controlo, indicado por um ponto no diagrama. Ou seja, ˆ C 12 | n 1 n 0 〉= | ( n 0 ⊕ n 1 ) n 0 〉 . No caso do operador ˆ C 21 o cbit de controlo é o segundo e o seu efeito é ˆ C 21 | n 1 n 0 〉= | n 1 ( n 0 ⊕ n 1 ) 〉 .

Vários qbits

O estado de um sistema de n qbits será uma combinação linear de 2 n estados próprios, representados pelos cbits com n algarismos binários. Pode ser representado por uma matriz complexa de uma coluna e 2 n linhas. Os operadores que atuam nesses estados são representados por matrizes unitárias, quadradas, com n linhas e n colunas.